岩石圈有效弹性厚度估算方法研究进展

侍 文，陈 石*，韩建成，贾路路

1 中国地震局地球物理研究所，北京 100081

2 北京白家疃地球科学国家野外科学观测研究站，北京 100095

0 前 言

地球岩石圈在地表和地下荷载的影响下进行重力均衡作用，发生相应的沉降或隆起，使荷载差异得到补偿. 根据均衡理论，地球内部地壳和地幔有趋于静力平衡状态的趋势（Watts, 2001, 2011）. 早期基于流体静力学平衡的Airy均衡（Airy, 1855）和Pratt均衡（Pratt, 1855, 1864）就是用于解释地球重力均衡现象的局部均衡模型. 后期人们发现，在某些区域（如夏威夷岛链）地表荷载没有完全得到补偿，且岩石圈的变形行为存在长周期特点（Watts, 2001）. 人们认为这是由于Airy和Pratt均衡模型只考虑地表和地下荷载的垂直作用力，模型假定的均衡补偿仅限于局部，只沿着垂直方向发生，而忽略了岩石圈本身的强度（Stoffa and Buhl, 1979;Vening-Meinesz, 1941）. Barrell（1914）指出地球岩石圈是具有较高强度的刚性板块, 有一定的抵抗形变的能力，足够支撑较大的区域性地质荷载. 经过进一步的研究，学者们提出了区域均衡模型（即弹性板均衡模型），用以描述地球岩石圈重力均衡状态以及均衡调整过程（Vening-Meinesz, 1932;Gunn, 1937, 1943; Watts, 2011）.

弹性板均衡模型认为岩石圈力学强度或抗变形能力，在岩石圈变形演化过程中起着重要作用. 在地质时间尺度上（＞106年），岩石圈力学强度影响着岩石圈对重力均衡响应的快慢和程度. 这些均衡响应信息是认识岩石圈内部结构和动力学特征的重要依据. 岩石圈有效弹性厚度（Te）是度量岩石圈力学强度的一个定量指标，也是研究岩石圈大规模构造的有力工具，与岩石圈热状态、流变学性质、力学特性等诸多物理因素相关，现在已经广泛应用于研究岩石圈力学结构及动力学过程等诸多领域（Forsyth, 1985; Watts, 2001; 付永涛等, 2005）.

近年来，随着数据处理技术的发展，岩石圈有效弹性厚度的估算方法也得到了迅速的发展. 目前，计算的方法主要有三大类：正演法、谱分析方法（包括：导纳法和相关性法）和屈服应力包络法（付永涛等, 2000; 陈波, 2013; Audet, 2019）. 本文详细介绍了这些方法的计算原理，并分析比较了它们的优缺点.

1 岩石圈挠曲与有效弹性厚度

地球岩石圈中存在各种形式的载荷，例如地球表面的山体、盆地、冰盖和沉积层等，地球内部的岩浆侵入和地层逆掩等（Watts, 2011; 陈波, 2013）.在均衡调整过程中，岩石圈对这些载荷的响应不仅取决于载荷的空间尺寸（或几何大小），还与载荷加载的时间尺度有关. 如图1 所示，载荷加载之后，在同震形变时间尺度上（0～120 s），地壳及地幔物质可视为一个整体的弹性半空间模型，表现出明显的弹性特征；在震后形变时间尺度上（～10年），地壳及深部物质可近似为弹性薄板耦合于黏弹性半空间体之上的模型；在相对较短的地质时间尺度上（冰川回弹时间尺度，～104年），整个岩石圈被视为弹性板，而上地幔以深的物质则是黏弹性半空间体；在地质时间尺度上（＞106年），岩石圈则被视为漂浮在非黏性流体的软流圈之上的弹性薄板（Watts, 2010）.

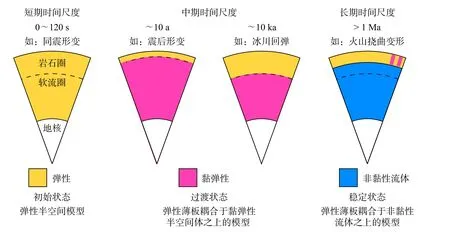
图1 地球外部圈层在载荷加载后不同时间尺度下的弹塑性响应（修改自Watts, 2010）Fig. 1 Schematic diagram illustrating how the Earth's outermost layers respond to loads of different timescales （modified from Watts,2010）

将岩石圈视为弹性薄板，该薄板受到加载其上载荷的作用，发生变形，该受力变形问题可以用弹性板挠曲方程表示（Turcotte and Suchubert, 2002）：

式中，w是弹性薄板的挠曲变形，x是水平坐标，ρm和ρinfill分别是地幔密度和挠曲凹地的填充物质密度，g是 重力加速度，ρload和hload是载荷的密度和高度，D是弹性薄板的挠曲刚度，可由有效弹性厚度Te求得：

式中，Te是岩石圈有效弹性厚度，E是杨氏模量，ν是泊松比. 利用公式（1）和（2）可以建立特定载荷加载下弹性薄板的挠曲变形与有效弹性厚度的关系.

岩石圈有效弹性厚度（Te）可定义为在真实载荷的作用下，能产生与实际岩石圈相等挠曲变形的理论弹性薄板的厚度（Forsyth, 1985; Watts, 2001;陈波, 2013）. 由公式（1）和（2）可知，Te可以决定岩石圈在载荷作用下产生挠曲变形的幅值和波长. 较大的Te代表岩石圈力学强度较高，不易于发生挠曲变形，此时岩石圈存在着一定程度的区域补偿，在载荷作用下，挠曲变形通常幅值较小且波长较长. 反之，较小的Te代表岩石圈力学强度较低，易于发生挠曲变形，在载荷作用下，岩石圈趋向于Airy均衡，挠曲变形的幅值较大，并且波长较小. 极端情况下，当Te=0时，代表岩石圈没有刚度，此时岩石圈不存在区域补偿，仅存在着局部补偿，遵循Airy均衡补偿模型.

岩石圈有效弹性厚度（Te）是一个能从实际观测中估计得到的参数，与众多地质构造的物理参数紧密相关，可广泛应用于研究岩石圈力学结构及动力学过程等诸多领域. 大洋岩石圈有效弹性厚度受控制于450±150 ℃等温面，并随着加载岩石圈载荷的年龄平方根增加而增加（见图2），与大洋岩石圈随年龄的沉降特征相似，表明其强烈依赖于岩石圈的热结构（Parsons and Sclater, 1977; Watts et al., 1980; Watts, 2001）. 相对于大洋，大陆岩石圈有效弹性厚度较为复杂，并且不对应于任何物质界面和深度，受多种参数的综合影响（Burov and Diament, 1995; Tesauro et al., 2009a, 2009b, 2012），主要包括：（1）岩石圈热结构和热年龄（Bechtel et al., 1990; 陈青, 2015）. 一般情况下，较老的热年龄对应较大的Te值，反之，较小的热年龄则与较低的Te值对应（Zuber et al., 1989）. 此外，较强烈的热活化作用，可以降低Te值（Watts, 2001;Tesauro et al., 2009b）. 因为岩石圈Te受其热结构和热年龄控制，所以Te与大陆岩石圈构造单元的年龄也存在着较密切的联系（见图2）. （2）地壳厚度的变化 （Burov and Diament, 1995）. 在存在软弱下地壳地区，地壳厚度的变化以及物质成分的差异容易导致壳幔的解耦、拆离作用（Burov and Diament, 1995; 焦述强等, 1996），而壳幔的拆离可能导致岩石圈力学强度减少一半之多（McNutt et al., 1988），引起Te值的减小. 也有研究认为地壳厚度与Te成正相关关系（袁炳强等，2002a，2002b）. （3）岩石圈内部应力状态.Te值依赖于垂向负载引起的挠曲变形，受水平应力较高时，解耦的岩石圈可引起不同尺度的地壳和岩石圈褶皱，而这些褶皱影响挠曲的计算，因此也影响着Te估计值（Cloetingh and Burov, 1996）. （4）板块边界负载. 在大陆碰撞带，板块之间的相互作用、相互叠置以及地幔下降流作用，使岩石圈局部力学强度发生显著变化，影响Te值（付永涛等，2000）. （5）断层位移和造山带走向. 沿断层的位移有助于岩石圈的均衡调整，可以降低其挠曲刚度，减少Te值（Bechtel et al., 1990; 付永涛等, 2005）. 造山带Te的空间变化，与造山带走向有一定的对应关系，是对先前岩石圈热性质和力学特征的继承结果，这种继承性可以影响随后的板块构造事件（Stewart and Watts, 1997）.

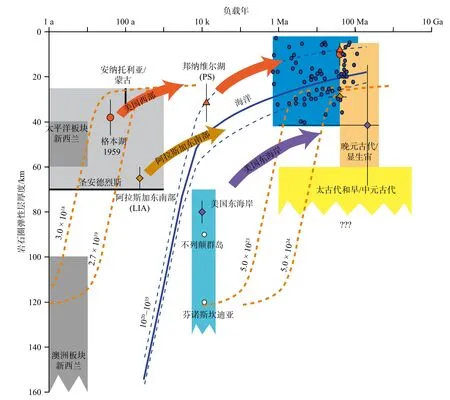
图2 岩石圈弹性层厚度与大洋及大陆岩石圈负载年龄之间的关系（修改自Watts, 2010）. 淡灰色矩形区域是基于岩石圈震后恢复数据估算的弹性层厚度与负载年龄之间关系所在的范围；这些数据来源于安纳托利亚（Hearn et al., 2002）、蒙古（Vergnolle et al., 2003）和黑格本湖（Nishimura and Thatcher, 2003）地区. 深灰色区域是基于希库兰吉海沟地区（Cohen and Darby, 2003）同震数据估算的范围. 青色区域是基于冰川回弹数据估算的范围；其数据来源于美国东海岸（Di Donato et al., 2000）、不列颠群岛（Peltier et al., 2002）以及芬诺斯坎迪亚（Milne et al., 2004）地区. 蓝色区域显示了Watts（2001）中表6.2的海洋岩石圈有效弹性厚度数据所在的范围，其中实心蓝色圆点是估算的数据点. 淡棕色和黄色区域是由大陆岩石圈有效弹性厚度数据估算得到的范围. 淡棕色区域的数据是基于晚元古代/显生宙地体估算的，而黄色区域的数据是基于太古代和早/中元古代地体估算的；这些数据来源于Watts（2001）以及Pérez-Gussinyé和 Watts（2005）. 其它的估算数据则是来源于阿拉斯加东南部（Larsen et al., 2005）、邦纳维尔湖（Nakiboglu and Lambeck, 1983）和美国西部（Lowry et al., 2000）地区. 蓝色实线和虚线是基于Watts 和Zhong（2000）的研究结果，推断的海洋岩石圈有效弹性厚度与负载年龄间的关系. 时间坐标值较小的两根棕色虚线（蓝线左侧）是根据理论模型估算的岩石圈有效弹性厚度和负载年龄间的关系曲线；该模型是一个假设30 km 厚的弹性层覆盖在黏弹性层之上的双层模型，两根虚线分别对应黏弹性层的黏度为～3.0×1018 和～2.7×1019 Pa s；曲线是利用 S. Zhong 的代码计算的（根据2003年的讨论）. 时间坐标值较大的两根棕色虚线（蓝线右侧）分别对应黏弹性层的黏度为～5.0×1023 和～5.0×1024 Pa s）Fig. 2 Plot of elastic layer thickness against the logarithm of load age （modified from Watts, 2010）. Light gray box shows the range of post-seismic rebound estimates. Data sources based on Hearn et al. （2002）, Anatolia; Vergnolle et al. （2003） Mongolia; and Nishimura and Thatcher （2003）, Lake Hegben. Dark gray boxes show the range of estimates associated with co-seismic deformation at the Hikurangi Trench （Cohen and Darby, 2003）. Filled light blue box shows the range of elastic layer thickness from glacial isostatic rebound. Data sources based on Di Donato et al. （2000）, East Coast, USA; Peltier et al. （2002）, British Isles; and Milne et al. （2004）, Fennoscandia. Filled dark blue box shows the range of oceanic Te estimates based on Table 6.2 of Watts （2001）. Filled blue circles show individual estimates. Filled light brown and yellow boxes shows the range of continental Te estimates from Late Proterozoic/Phanerozoic and Archean and Early/Middle Proterozoic terranes, respectively.The sources of data are given in Watts （2001） with the additional estimates of Pérez-Gussinyé and Watts （2005）. Other estimates are based on Larsen et al. （2005）, SE Alaska; Nakiboglu and Lambeck （1983）, Lake Bonneville; and Lowry et al.（2000）, Western USA. Solid and dashed blue lines show the predicted relationship between Te and load age for the oceanic lithosphere based on Watts and Zhong （2000）. Dashed brown lines to the left of the blue lines show the predicted relationship between Te and load age for a two-layer model of a 30-km-thick elastic layer that overlies a viscoelastic layer with viscosity of～3.0×1018 and ～2.7×1019 Pa s. The curves have been computed using the code of S. Zhong （pers. comm., 2003）. Dashed brown lines to the ‘right’ of the blue lines show the relationship for viscosities of ～5.0×1023 and ～5.0×1024 Pa s

2 有效弹性厚度估算方法

2.1 正演法

正演法是通过对比分析重力异常实际观测值与不同载荷及挠曲情况下岩石圈薄板产生的重力异常理论值、确定岩石圈挠曲模型、最终估算出岩石圈有效弹性厚度的方法. 根据挠曲理论，漂浮在软流圈之上的岩石圈在各种载荷（例如：造山带、火山、海山、洋中脊地形、消减带、冰川和沉积层等）作用下，产生的挠曲变形可用四阶偏微分方程[公式（1）]来求解（付永涛等，2005；陈波，2013）.基于设定条件下求解得到的挠曲变形和实际地形，构建岩石圈密度结构模型，通过正演模拟计算该模型所对应的重力异常理论值，并与实际观测值进行比较，不断修改设定的岩石圈模型，直至该模型重力异常理论值与观测值吻合程度较高时，停止修改，根据该最终的岩石圈模型，获取岩石圈的弹性参数（刚度或弹性厚度）（Karner and Watts, 1983;Lyon-Caen and Molnar, 1984; Watts, 2001, 2010）.对于正演法中涉及的挠曲计算问题，在简单载荷加载情况下可以由公式（1）求出解析解，例如：变化较为规律的周期性载荷、岛链或火山链等线性载荷（Hetényi and Hetbenyi, 1946; 陈波, 2013）. 在复杂的二维和三维载荷情况下，岩石圈的挠曲计算无法得到解析解，需要采用数值方法求解（Stewart,1998），如有限差分法等（Sheffels and McNutt,1986; Van Wees and Cloetingh, 1994; Jin et al., 1996;Stewart and Watts, 1997; Jordan and Watts, 2005）.

在岩石圈结构较为简单，载荷和挠曲较为明确的地区，正演法比谱分析方法（导纳法和相关性法）准确. 但是，在岩石圈及地质结构复杂的地区，载荷和挠曲很难被分辨清楚，同时，正演过程中岩石圈实际密度结构无法被充分的考虑和模拟，使得正演法受到严重限制，很难被广泛应用（Watts,2001）.

2.2 谱分析方法

谱分析方法是利用地形和重力异常数据估算岩石圈有效弹性厚度（Te）的方法，是目前用于估算大陆和大洋地区Te最常用的手段. 谱分析方法最早由Dorman和Lewis（1970）提出. 此类方法利用岩石圈在荷载作用下，地形和布格重力异常二者在波数域中关系的变化特征来估算岩石圈Te（Dorman and Lewis, 1970; Watts, 2001; 陈波, 2013; 陈石等,2014）. 谱分析方法包括：导纳法和和相关性法.

2.2.1 挠曲响应函数

真实的岩石圈载荷通常可以近似为周期性载荷，此时，公式（1）可以表示为：

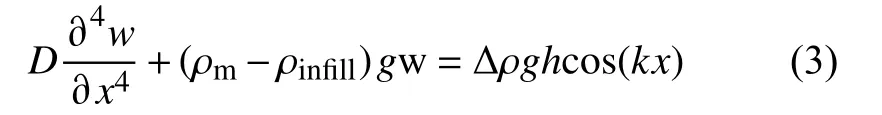
式中，Δρ为上覆介质与地壳之间的密度差，h为最大地形起伏. cos()函数表示周期性载荷，因为地形通常可看成不同周期特征的分量求和形式，k为荷载在x方向上的傅里叶波数.

方程（3）的解有如下形式（Watts, 2001）：

上式中，右端项与D有关的部分，被定义为挠曲响应函数（flexural response function）Φe()，即：

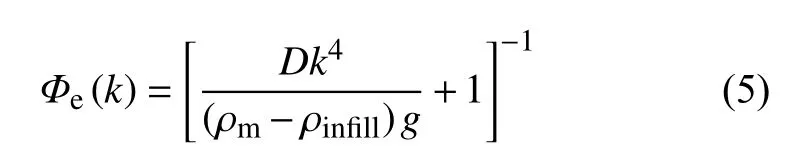
式中，Φe是波数k的函数，当密度差确定时，在不同的波数k下，仅与挠曲刚度D相关.

图3是挠曲响应函数Φe在不同的岩石圈Te下，随波数k变化的理论曲线（Watts, 2001）. 当波数k趋向于0时，岩石圈会表现为Airy响应特征，即当载荷尺寸很大时，岩石圈表现出力学强度很低的特征，此时，岩石圈在载荷作用下发生挠曲变形，均衡调整之后的“山根”仅与山的高度有关. 相反，当波数k趋向于无穷大时，岩石圈会表现为Bouguer响应特征，即当载荷尺寸很小时，岩石圈表现出力学强度很高的特征，此时，岩石圈的强度大到足够支撑上覆的载荷，而不发生挠曲变形. 当岩石圈Te变化时，挠曲响应函数随载荷波数的变化趋势也会发生相应变化（如图3所示）. 值得注意的是，仅在“挠曲特征波段”（diagnostic waveband of flexure）范围内（即0.001＜k＜0.1时），这些曲线 才可以被用于估算岩石圈Te.

图3 挠曲响应函数（修改自Watts, 2001）Fig. 3 The diagram of lithospheric flexural response function （modified from Watts, 2001）

2.2.2 导纳法

Lewis和Dorman（1970）利用实测的地表地形和重力异常的功率谱求得了观测导纳函数，并与由Airy模型计算得到的导纳函数比较，分析了北美大陆的补偿密度分布. McKenzie 和 Bowin（1976）利用海底地形和海洋自由空气重力异常的导纳谱研究了大西洋的岩石圈有效弹性厚度. Banks 等（1977）通过地形和布格重力异常的导纳估算了北美大陆岩石圈的有效弹性厚度. 随后，导纳法被广泛应用于其它地质特征区域的岩石圈有效弹性厚度研究（McNutt and Parker, 1978; Cochran, 1979;Detrick and Watts, 1979; McNutt, 1980; Louden,1981; Karner and Watts, 1982; Ribe and Watts, 1982;McKenzie and Fairhead, 1997; McKenzie, 2003; 陈石等, 2011; 胡敏章等, 2015; 付广裕等, 2020）.

如果将岩石圈看成滤波器，地形载荷是输入信号，挠曲变形是输出，重力异常就是这种输出量的可观测部分. 在波数域，我们用导纳（gravitational admittance）来表示这个关系：

式中,Z(k)为重力导纳，Δg(k) 为波数域的重力异常,H(k) 为波数域的地形.

基于位场理论，Parker（1973）将频率域的界面起伏与重力异常之间的关系用泰勒级数展开表示，由于岩石圈有效弹性厚度对高频地形成份不敏感，因此可以略去高阶系数，仅保留一阶近似，即：

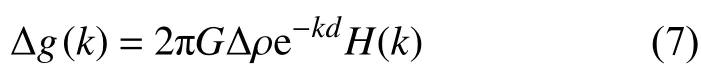
式中，d为平均界面起伏，G为万有引力常数，Δg(k)为重力异常. 在不同岩石圈有效弹性厚度情况下，根据式（7）的地形谱与重力异常谱之间的近似关系，可以进一步推导重力导纳的理论公式，得到复合模型（如图4所示）的导纳公式如下（Forsyth,1985）：

式中，Z(k)surface+buried为波数域导纳函数，=, ρc为地壳平均密度，Zt为地壳平均厚度，k为平面上的波数,Ht为板上加载对地形的贡献量，Hb为板下加载对地形的贡献量，两者之和与观测地形相等，具体含义如图4所示.

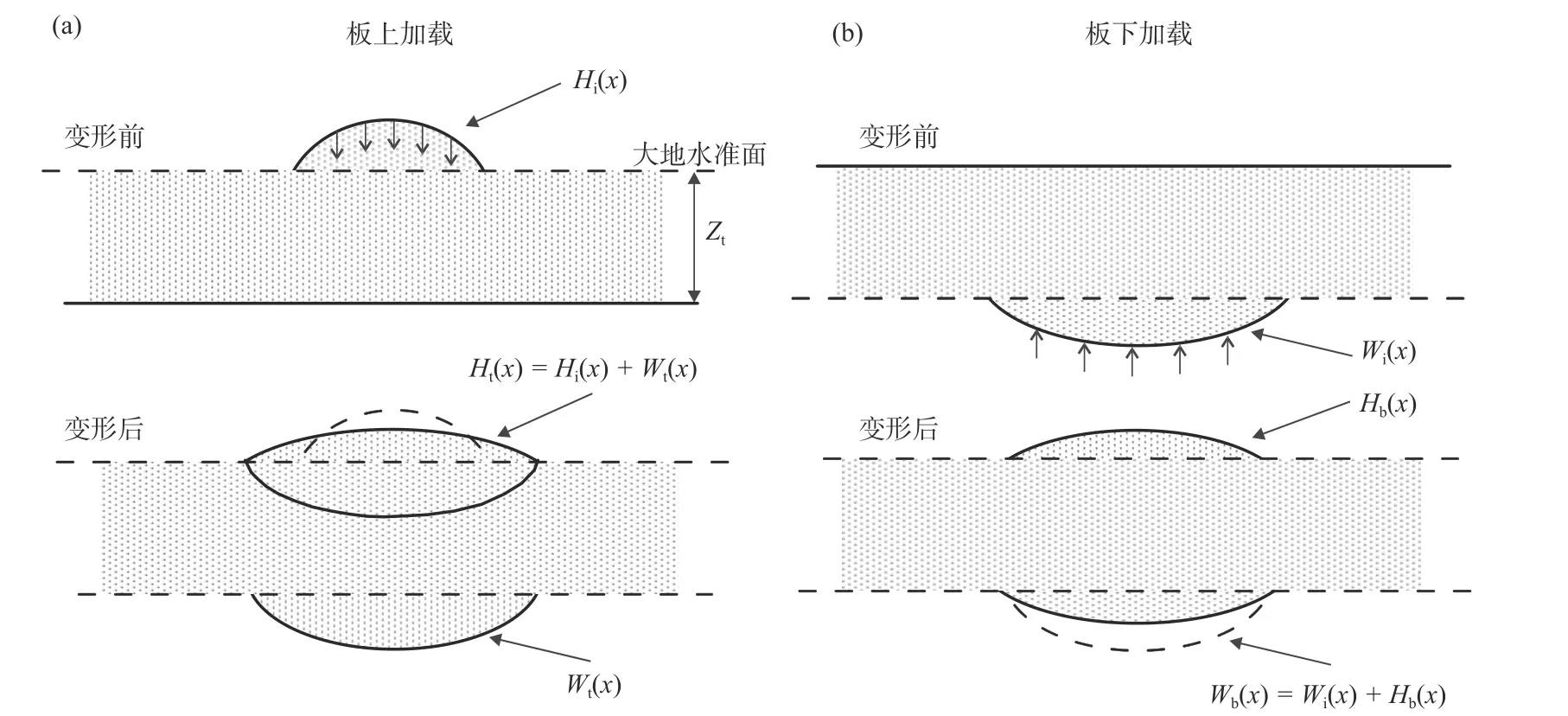
图4 岩石圈有效弹性厚度导纳法计算复合模型示意图（修改自Watts, 2001）. 其中：Zt为地壳厚度，Hi 表示变形前板上地形，Wi表示变形前等效板下变形，Ht 表示变形后由于板上加载剩余的地形，Wt 表示变形后板上加载引起的等效板下变形，Wb表示变形后由于板下加载的等效剩余变形，Hb 表示由于变形后板下加载引起的板上地形Fig. 4 The diagram of composite model used for calculating lithospheric effective elastic thickness based on admittance method（modified from Watts, 2001）. Ztis the crustal thickness，Hiis the surface topography before deformation，Wi is the height of the buried load before deformation，Ht is the contribution of surface loading to the topography，Wt is the contribution of surface loading to the buried load after deformation，Wb is the equivalent topography of the buried load after deformation，Hb is the contribution of buried load to the topography after deformation

假定板下与板上加载贡献的比值为f，定义其为（Forsyth, 1985）：

将式（9）代入式（8），得：

初始载荷比F代表岩石圈在发生挠曲变形之前内部不同密度界面的加载比例关系，由式（11）表示（McKenzie, 2003; Kirby and Swain, 2009）：

通过以上式（2）、（5）、（10）和（11），给定两个独立参数 (Te,F)，即岩石圈有效弹性厚度和初始载荷比, 就可以计算理论模型导纳值. 然后，在已知重力异常和地形的基础上，将理论模型导纳计算结果和实际数据进行对比，通过反演的方法，获取岩石圈有效弹性厚度和初始载荷比的空间分布.

2.2.3 相关性法

除导纳法以外，相关性法也是反演Te和初始载荷比F的重要谱分析方法. 岩石圈受到载荷作用时，产生挠曲变形，地表地形和岩石圈下部密度分界面发生相应调整，岩石圈密度结构发生改变，产生重力异常，地表地形和布格重力异常之间存在一定的相关性，而通过该相关性的变化，可以确定岩石圈的弹性参数（Watts, 2001; 陈波, 2013）.

相关性法最早由Forsyth（1985）提出. 对于波长较长的荷载，岩石圈更趋向于区域均衡模式，岩石圈挠曲变形较为明显，此时的重力异常与地表地形可能完全相关，即二者的相关度趋向于1；而对于波长较短的荷载，由于岩石圈本身的刚度，其可以一定程度上支撑载荷，使得岩石圈挠曲变形较小，此时重力异常与地表地形相关度较小，二者的相关度趋向于0. 岩石圈重力异常与地表地形相关度随载荷波长从1变化为0处的波长，被称为转折波长. 转折波长代表岩石圈从区域均衡变为不均衡的状态，其大小与岩石圈刚度有关（Forsyth, 1985;Watts, 2001; 陈波, 2017）. 通常，岩石圈有效弹性厚度越大或刚性越强，其对应的转折波长越长.

通过实际观测的地表地形和布格重力异常，计算二者之间随波长变化的波数域相关度（实测相关度），并与理论弹性板模型求解的预测相关度比较，反演岩石圈有效弹性厚度及初始载荷比. 相关性法对不同均衡响应模式下的转换波长较为敏感，计算精度较高.

利用重力异常和地形的互功率谱和自功率谱，实测相关函数可表示为（McKenzie and Bowin, 1976;Forsyth, 1985）：

式中，〈〉表示平均谱.

复合模型（如图4所示）的理论相关函数为（Forsyth, 1985）：

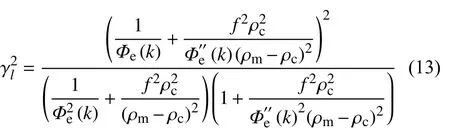
与上述导纳法类似，通过式（2）、（5）和（13），给定参数（Te,F），可以计算理论模型相关函数值，然后，再将此理论相关函数值与由式（12）得到的实测相关函数值对比，用于反演计算，获取最优的Te和F解.

相关法和导纳法的原理类似，但是相关法估算岩石圈有效弹性厚度时受荷载比的影响比导纳法小很多. 随着卫星重力技术的发展，基于地表地形和布格重力异常的相关法逐渐成为了目前估算岩石圈有效弹性厚度的最流行方法（陈波，2013）.

2.2.4 功率谱估计

基于谱分析方法估算岩石圈Te时，需要计算地表地形和重力异常的功率谱. 1990年代开始，学者们大多采用周期图法估算地形和重力异常的功率谱（Percival and Walden, 1993）. 周期图法是一种常用的直接利用离散傅里叶变换计算信号功率谱的方法. 但是，周期图法存在着频谱泄漏的问题. 直接采用傅里叶变换来估算功率谱，会因为计算窗口尺寸的选择不合适，而引入较大的误差（Karner and Watts, 1982; Lowry and Smith, 1994）. 在岩石圈Te较为均一时，较小的计算窗口可以准确地估算出Te结果，但是当岩石圈Te不均匀，在某处存在较大值时，估算结果则会出现较大的偏差（Kirby, 2014）.当计算窗口选择较大时，计算区域过大，容易将存在不同Te值的区域合在一起计算，导致估算结果出错（Simons and Olhede, 2013; Kirby, 2014）. 除了窗口尺寸选择不合适外，窗口类型不匹配、混叠、吉布斯现象等，也会导致周期图法的频谱泄漏问题. 为了改进周期图法的频谱泄漏问题，学者们在做傅里叶变换之前，对信号进行了一些必要的处理，比如：补零、信号及边缘补偿、趋势分离、边缘镜像等（Dorman and Lewis, 1970; McKenzie and Bowin, 1976; Banks and Swain, 1978; Watts, 1978;Detrick and Watts, 1979; McNutt, 1979; Karner and Watts, 1982; Louden and Forsyth, 1982; Ribe and Watts, 1982; Dixon et al., 1983; Bechtel et al., 1987;Zuber et al., 1989; McKenzie and Fairhead, 1997;Audet and Mareschal, 2004a）.

Lowry和Smith（1994）以及Lowry和Smith（1995）采用最大熵法（maximum entropy spectral estimation, MESE）（Burg, 1975）估算了二维地形和布格重力异常的功率谱. 最大熵法根据最大熵准则将信号未知延迟点的自相关函数外推以估算功率谱，避免了较小计算窗口对频谱估计的影响（Burg,1975; Simons et al., 2000）. 同时，Lowry和 Smith（1994）也在研究过程中发现了最大熵法的不足之处，该方法在频谱估计中引入的虚假谱峰、峰值分裂、相位差等现象会影响岩石圈Te估算的准确性.

McKenzie和 Fairhead （1997）以及Simons等（2000）将多窗谱分析技术（multitaper）（Thomson,1982）引入到导纳法和相关性法中. 多窗谱分析技术首先会构造一组频谱泄漏最小的正交序列窗口（称为Slepian序列），然后将这组窗口分别作用于信号的傅里叶变换中，得到一组独立的谱，最后对这组谱进行加权平均，获得一个低方差的平滑谱估计，同时降低谱估计的频谱泄漏效应（Slepian,1978; Thomson, 1982）. 由于多窗谱分析技术在改善谱估计的频谱泄漏方面效果明显，该方法被广泛用于岩石圈有效弹性厚度的研究中（Simons et al.,2003; Audet and Mareschal, 2004b; Pérez-Gussinyé et al., 2004; Pérez-Gussinyé and Watts, 2005）. 但是, 由于多窗谱分析技术反演岩石圈Te时，滑动窗口的大小固定，限制了反演的转折波长，导致Te反演结果偏低（Simons et al., 2000; 陈波, 2013）. 另外，该技术中Te反演结果的分辨率也会和窗口的大小相互制约：小尺寸窗口不能解析转折波长大于反演窗口的Te信息；大尺寸窗口不能获取Te的小尺度变化（Stark et al., 2003; 陈波, 2013）. Pérez-Gussinyé等（2007, 2009a, 2009b）对多窗谱分析技术中固定窗口对反演转折波长的限制进行了分析，提出了多个窗口联合使用的方案，并认为该方案可以精确地反演出Te梯度和小尺度Te的变化.

小波谱分析也是一种常用的估算地形和重力异常功率谱的方法（Grossmann and Morlet, 1984）.Stark等（2003）最先将高斯张量小波引入到岩石圈Te的反演中. Kirby 和Swain （2004） 基于叠加的Morlet小波构建了一种可行的Fan小波，用于岩石圈Te研究中的功率谱估计. 基于Fan小波技术的谱分析方法，通过小波空间域和波数域的多尺度变化，可以克服多窗谱分析技术中Te结果分辨率和分析窗口大小相互制约等问题，能同时反演不同尺度的Te分布（Kirby, 2005; Swain and Kirby, 2006;Kirby and Swain, 2011; 陈波, 2013）. 该方法已经被应用于研究澳大利亚（Swain and Kirby, 2006）、南美（Tassara et al., 2007）、加拿大地盾（Audet and Mareschal, 2007）、小笠原—马里亚纳海沟（Bai et al., 2018）、太平洋（Lu et al., 2021）、中国大陆及邻区（Chen et al., 2013; 陈波, 2013）、中国西部大陆（Chen et al., 2014, 2015）和中国南部（Mao et al., 2012）等地区的Te结构. Audet和Bürgmann（2011）还利用此方法研究了全球大陆的岩石圈有效弹性厚度及各向异性（如图5所示）.

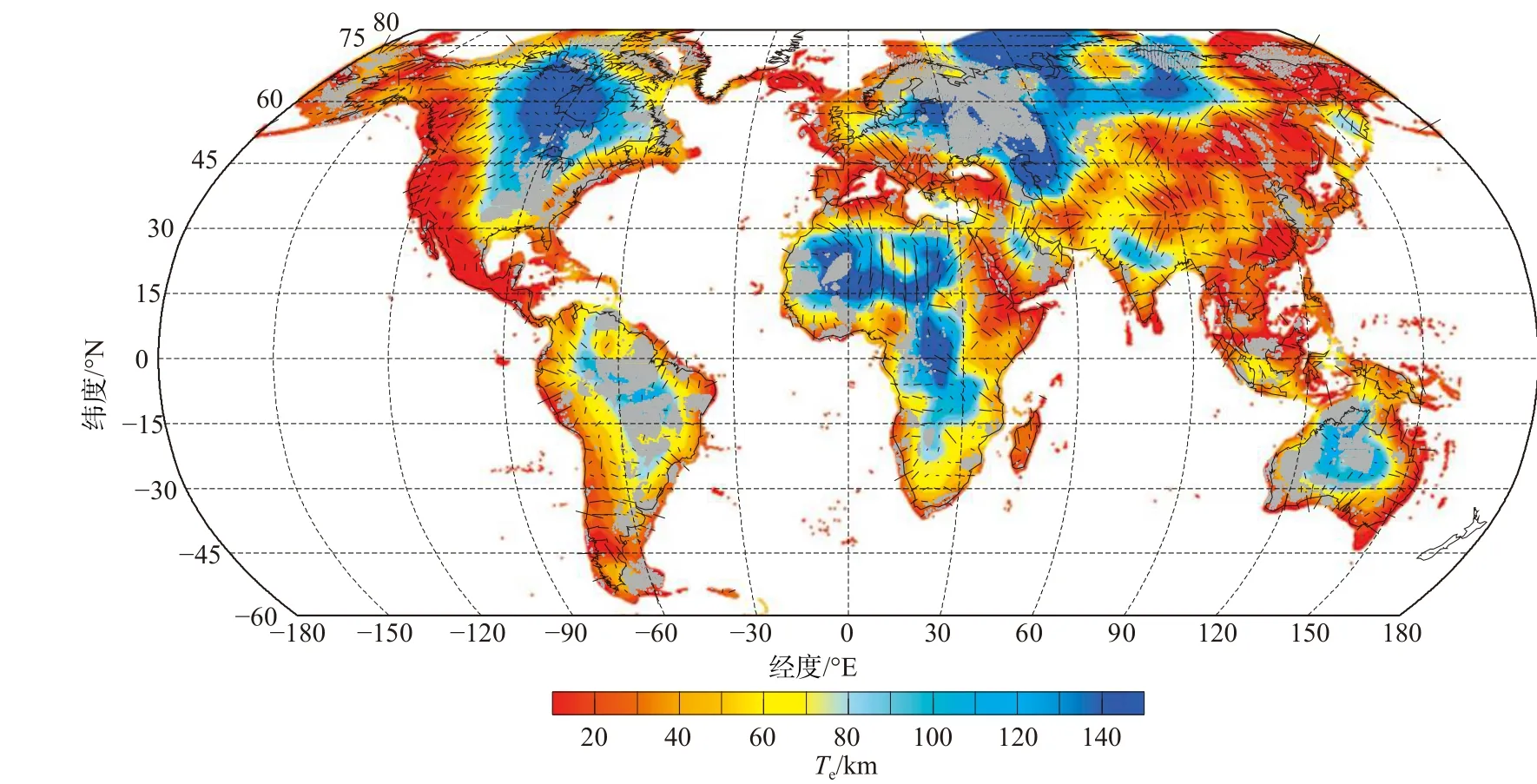
图5 全球大陆岩石圈有效弹性厚度及其各向异性（修改自Audet and Bürgmann, 2011）. 其中，黑色短线的方向代表Te各向异性的方向，黑色短线的长度与Te各向异性的大小成正比，彩色底图是Te值大小的横向分布Fig. 5Global effective elastic thickness over continents calculated from the coherence between Bouguer gravity and topography using wavelet method （modified from Audet and Bürgmann, 2011）. Teanisotropy superposed on colour-contoured Te over continents and continental shelves. The direction of the black bars represents the Te anisotropy direction. The length of black bars is given by the magnitude of Te anisotropy

2.3 屈服应力包络法

屈服应力包络法，又被称为热流变结构方法，是一种基于实验岩石力学数据估算岩石圈有效弹性厚度的方法（Goetze and Evans, 1979; Bodine et al.,1981; 陈波, 2013）. 实验岩石力学认为岩石圈的上部主要表现为脆性变形，而在中下部主要表现为塑性流动变形. 岩石圈上部的脆性变形特征可以由Byerlee岩石线性摩擦破裂公式描述（Byerlee,1978），而下部的塑性流动变形特征可以由Dorn指数蠕变定律来确定（Goetze, 1978）. 岩石圈发生脆性变形的部分，岩石圈强度随着压力和深度的增加而增加；在发生塑性流动变形的部分，岩石圈强度随温度和深度的增加而减少（Byerlee, 1978;Goetze, 1978）. 结合脆性和塑性变形两种定律，就可以得到岩石圈强度随深度变化的特征的屈服应力包络面（Goetze and Evans, 1979）. 屈服应力包络法是在已知岩石圈温度场的前提下，通过分层流变学计算岩石圈随深度变化的力学强度.

屈服应力包络法最早被应用于估算大洋地区的岩石圈有效弹性厚度，并取得了较好的效果（Bodine et al., 1981; Lago and Cazenave, 1981;McNutt and Menard, 1982; McAdoo et al., 1985）. 这些研究表明：大洋岩石圈有效弹性厚度主要受温度结构控制，并随着加载岩石圈载荷的年龄增加而增加. 随后，学者们也将屈服应力包络法应用于大陆地区岩石圈有效弹性厚度的研究中（Karner and Watts, 1983; McNutt et al., 1988; Burov and Diament,1992; Burov and Diament, 1995）. 研究认为大陆地区的岩石圈结构复杂，除岩石圈的温度场外，还有许多其它因素会对屈服应力包络产生影响，包括：地壳厚度、地壳组成成分、应变率、地幔岩石圈厚度和流体分布等. 最近，Tesauro等（2009a, 2009b）利用屈服应力包络法研究了欧洲及全球大陆地区的岩石圈有效弹性厚度.

由于大陆岩石圈的复杂性，目前，屈服应力包络法也存在一定的争论（Maggi et al., 2000;Jackson, 2002; Watts and Burov, 2003; Burov and Watts, 2006; Burov, 2011; 陈波, 2013）. Burov 和Diament（1995）提出的“三明治”模型（Jelly Sandwich Model）认为大陆岩石圈力学强度分布为：上地壳强度高、下地壳强度弱、上部地幔强度高、下部地幔强度弱. 而Jackson （2002）提出的“法式焦糖布丁”模型（Crème brûlée Model）则认为大陆岩石圈的上地壳强度较高，而地幔强度较弱.屈服应力包络法是基于岩石力学实验获得岩石圈的力学强度的，该方法虽然可以提供重要的岩石圈强度估计和流变信息，但是时间尺度、应变率、温度以及加载条件等实验环境，与实际地球的情况可能存在一定的差距，导致岩石圈强度估算结果偏离实际值，所以该方法应用过程中我们需要充分考虑各方面的不确定因素.

2.4 岩石圈Te各向异性

近年来研究表明Te在空间上存在着各向异性，相比SKS横波分裂和地震波径向各向异性，Te各向异性更与垂直受力状态相关，是研究岩石圈变形和流变特性的重要参数之一（Stephenson and Lambeck, 1985; Owens and Zandt, 1997; Kirby and Swain, 2006; Mao et al., 2012）. 岩石圈Te各向异性代表岩石圈在不同水平方向上的力学强度差异.Te各向异性的方向（弱轴方向）代表岩石圈强度较弱的方向. 在板块汇聚带，Te各向异性的方向一般与岩石圈的最大压应力方向或物质流动的方向一致（Kirby and Swain, 2006）. 在岩石圈形变过程中，地震波各向异性的方向（快波偏振方向）与最大压应力方向趋于平行（Crampin, 1978; 高原等, 1994）.如果Te各向异性的方向与地震波各向异性的方向平行，则说明岩石圈物质可能存在侧向流动；相反，如果Te各向异性的方向与地震波各向异性的方向垂直，则说明岩石圈可能处于垂直连续变形模式（Audet et al., 2007; 李永东等, 2013）. 据此，通过比较Te各向异性与不同深度上的地震各向异性，可以获得岩石圈垂直连贯性变形的深度，以及岩石圈不同圈层耦合程度信息（李永东等，2013）. 例如，Audet等（2007）认为在松潘—甘孜块体地区可能存在物质侧向流动，因为该地区Te各向异性与SKS快波偏振方向近似平行.

Simons 等（2000, 2003）利用多窗谱分析技术研究了澳大利亚地区的Te各向异性，发现澳大利亚Te各向异性和地震波各向异性在200 km以上具有很强相关性，推断该地区200 km以上的大尺度变形是连续的. Audet 和Mareschal（2004b, 2007）分别利用多窗谱和Fan小波技术研究了加拿大地盾的Te各向异性. Mao 等（2012）、郑勇等（2012） 和李永东等（2013）采用Fan小波法分别对中国华北、华南和青藏高原东北缘的Te各向异性进行了研究，讨 论了Te各向异性和岩石圈形变的内在关系.

3 总结与展望

本文系统地介绍了岩石圈有效弹性厚度的研究背景和基本估算原理，总结了国内外岩石圈Te估算方法的研究进展. 岩石圈有效弹性厚度（Te）这一度量岩石圈力学强度的重要指标，现已广泛应用于研究岩石圈热状态、流变学性质、力学特性等诸多物理过程，同时也是研究岩石圈力学结构、大规模构造及动力学过程的重要工具.

正演法、谱分析方法（包括：导纳法和相关性法）和屈服应力包络法是目前估算岩石圈Te的主要方法，其中谱分析方法最为流行. 谱分析方法中，最早被用于估算岩石圈Te的是导纳法，该方法的特点是物理意义明确，易于理解和实现，而相关性法的特点则是对不同均衡响应模式下的转换波长更敏感，容易得到较高的Te计算精度. 随着卫星重力技术的发展，相关性法逐渐成为目前估算岩石圈Te最流行的方法. 近年来，随着数字信号处理技术的不断进步，估算地形和重力异常功率谱的方法也得到了长足的发展. 周期图法、最大熵法、多窗谱分析和小波谱分析技术的应用，使得地形及重力异常功率谱估计的准确性越来越高，基于此获得的岩石圈Te也越来越准确.

尽管如此，关于岩石圈有效弹性厚度的研究仍然存在巨大发展空间. 目前，在研究岩石圈有效弹性厚度及其各向异性时，往往仅采用导纳法或相关性法中的一种方法估算Te值及其各向异性，导致估算结果误差较大，同时，不同的反演方法和模型参数的选择，获得的有效弹性厚度结果差异性明显，计算结果不易解释（Kirby, 2014; Chen et al., 2015）.Audet （2019）提出的导纳—相关性谱分析联合反演方法，可同时使用导纳法和相关性法两种方法计算Te，计算结果较为可靠，但是，该方法是基于各向同性模型开发的，目前还无法计算岩石圈Te的各向异性. 我们将来需要进一步发展导纳—相关性谱分析联合反演方法，使其能够估算岩石圈Te的各向异性.

基于各向异性模型获得的岩石圈Te通常更为准确，可利用此结果，计算地质特征区均衡重力异常模型，分析异常特征，了解地下构造环境，以及对比Te和F值横向变化与地震分布、地壳厚度分布、构造单元年龄和磁性构造层底面深度等深部结构参数，分析探讨各自相关性，探索其地质意义和内在的动力学信息.

致谢

感谢审稿专家在本文写作和修改过程中提供的意见和建议.