相位相关性增强的自适应低重叠率多光谱图像快速拼接算法

贾停停，王慧琴*，王 可，王 展，甄 刚，李 源

（1. 西安建筑科技大学 信息与控制工程学院，陕西 西安 710055；2. 陕西省文物保护研究院，陕西 西安 710075；3. 西安博物院，陕西 西安 710054）

1 引 言

多光谱图像为通过光谱相机获取到的不同通道的多幅图像，具有光谱分辨率和空间分辨率。近年来，多光谱成像技术在图像处理领域有很大突破，大多用于遥感图像［1-2］，也有学者将其应用于文物保护领域且取得了一定成就，如壁画的保护与修复［3-4］。在实际拍摄过程中，多光谱图像的宽视角和高分辨率两方面需求存在冲突，可利用图像拼接技术将多幅窄视角、高分辨率的多光谱壁画图像拼接并融合，获得具有宽视角、高分辨率的多光谱壁画图像［5-7］，为壁画的保护与修复提供更详实的数据。

图像拼接一般包括图像采集与预处理、图像配准，图像融合3 个步骤，其关键步骤为图像配准［8-9］。在图像配准领域，Harris［10］等提出Harris检测算子，虽算法稳定性高，但不具备尺度不变性；Lowe［11］提 出SIFT 特征匹配算法，具有尺度不变性和旋转不变性，配准精度高、鲁棒性强但时间成本大；Bay［12］等在对SIFT 算法降维的基础上提出SURF 算法，虽将配准速度大幅提高，但其 精 度 有 所 降 低；陈 伟［13］等 将FAST 算 法 与SURF 算法进行结合，进一步提升了算法的匹配速率，但在精度上还是有所欠缺。Rublee［14］等将Fast 算法与Brief 算法进行融合提出ORB 算法，提高了特征检测和特征匹配速率，但特征点检测不 稳 定，配 准 精 度 不 及SURF 算 法。Wu［15］将BRISK 算法和ORB 算法结合，提升配准精度的同时提升了配准速率，但精度还是低于SIFT 与SURF 算法。以上算法均在配准精度与效率之间存在一定冲突，且不可直接获取图像之间的偏移量，无法实现多光谱图像的准确快速拼接。

基于二维傅里叶变换的相位相关法具有算法简单、精确度高的特点［16］。该方法由Kuglin［17］等首次提出，可计算出两张重叠率较大图像之间的偏移量，但无法对重叠率低，以及具有较大旋转角度和尺度变化的两幅图像实现精确配准。Reddy［18］等将对数极坐标变换与相位相关法融合形成扩展相位相关法，解决了同时具有平移、旋转和尺度变换的两幅图像的配准问题。Li［19］等提出一种基于图像金字塔改进的相位相关配准算法，在引入金字塔分解降低图像分辨率的基础上结合相位相关法，降低了算法复杂度且对目标部分丢失或被遮挡的情况具有很强的鲁棒性。因壁画拍摄现场情况复杂，需对目标壁画进行快速数据采集，因此采集的壁画多光谱图像分镜头间重叠率较低。上述针对相位相关法的改进均无法克服其在低重叠率时的误匹配问题，无法实现低重叠率多光谱图像的快速拼接。

本文提出一种相位相关性增强的自适应低重叠率多光谱图像快速拼接算法。在相位相关法的基础上，设计图像相关性增强切分方法，增大相邻分镜头下两幅壁画光谱图像之间的重叠率，引入最小二乘法进行自适应偏移量寻优，然后利用相邻分镜头图像各通道偏移量一致原则，将基准通道图像偏移量定位映射到其他通道，实现低重叠率壁画光谱图像多通道快速拼接。最后，使用本文算法与Harris、SIFT、FAST-SURF、BRISK-ORB 四种算法进行多光谱图像拼接对比实验，评价并讨论了实验结果。

2 相位相关法基本原理

在现有图像匹配算法中，相位相关法具有计算量小、抗噪声等优点，可精确计算出图像之间的相对偏移量，能快速高效地实现光谱图像的多通道拼接。当待拼接图像之间仅有平移关系时，设两者图像信号分别为f1(x，y)、f2(x，y)，则两幅图像满足以下条件：

式中，dx、dy为两张图像水平偏移量和竖直偏移量［16］。根据傅里叶变换位移性质，将图像变化通过频域反映得：

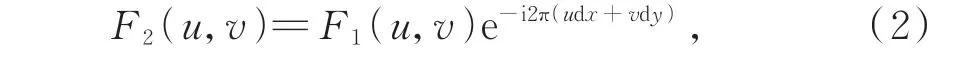
式中：F1(u，v)为 图像f1(x，y)的 傅里叶变换，F2(u，v)为图像f2(x，y)的傅里叶变换，两幅图像的归一化互功率谱如下：

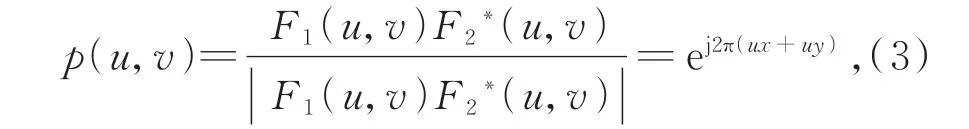
式中，F表示F2的复共轭，|F1(u，v)F(u，v)|为F1(u，v)F2∗(u，v)的幅度谱。根据傅里叶变换平移定理，对互功率谱进行傅里叶逆变换可得两幅图像的相位相关函数为：

式中，δ(x-dx，y-dy)为脉冲函数［20-21］。当两幅图像仅有平移差异时，脉冲函数峰值所在的位置对应两幅图像的相对偏移量［22］，峰值大小表示两幅图像的相关度，即当两幅图像完全相同时，脉冲函数峰值为1。当两幅图像配准成功时，其脉冲函数峰值个数唯一，如图1（a）所示；当配准误差较大时会存在多个比较接近的峰值，如图1（b）所示。

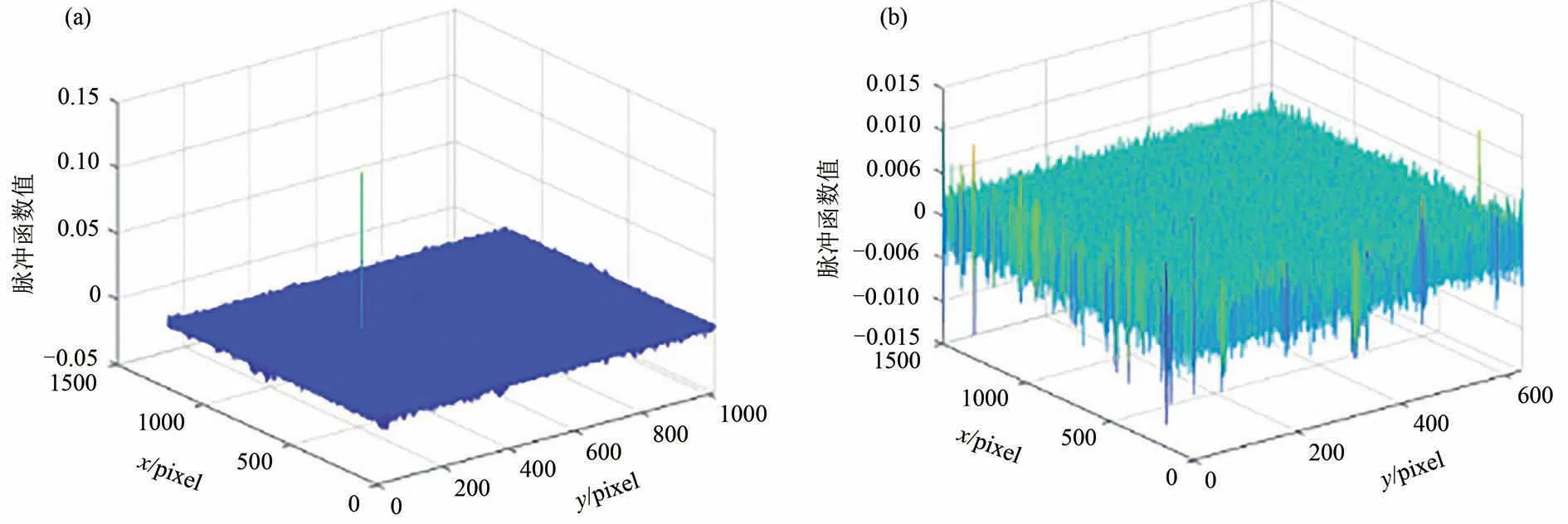
图1 图像的相位相关函数脉冲图。（a）正确匹配脉冲图；（b）错误匹配脉冲图。Fig.1 Pulse diagram of phase correlation function of image.（a）Correctly match the pulse diagram；（b）Error matching pulse diagram.

当重叠区域所占比例过小时，两幅图像相关性低，相关峰能量会向非相关峰扩散，造成多峰值干扰，相位相关法无法精确获取两幅图像的相对偏移量。故其在图像重叠率大于50%时具有较好的拼接效果，重叠率较低时容易产生误匹配。

3 相位相关性增强的低重叠率多光谱图像拼接算法

3.1 图像相关性增强切分法

相邻分镜头光谱图像重叠率较低时，直接使用相位相关法进行拼接会造成较大误差。为保证匹配准确性，设计图像切分方法，逐步切除光谱图像的非重叠部分，提高两幅子图像的重叠率，以增强子图像相关性。设图像宽为c，切分总次数为num，则切分步长l为：

每次切去一个步长的像素，则第i次切分后剩余子图像宽度为：

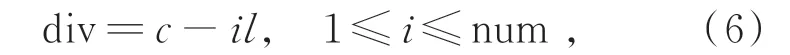
切分示意图如图2 所示。

图2 图像切分示意图Fig.2 Schematic diagram of image segmentation

3.2 自适应相位相关性增强图像拼接算法

3.2.1 最小二乘偏移量寻优

不同大小子图像配准结果存在差异。为寻找最佳匹配结果并保证结果的准确性，引入最小二乘法对匹配结果进行验证，实现偏移量寻优，保证算法的精确度。通过使误差的平方和最小化去寻找与数据匹配的最佳函数［23］，形式如下：

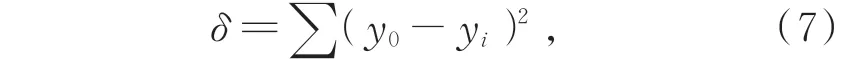
式中：δ为累计误差，yi为预测值，y0为真值。

选取匹配结果对应的两幅图像的重叠部分进行验证，利用相位相关法计算重叠部分的相对偏移量dx、dy，其偏移量累计误差最小为：

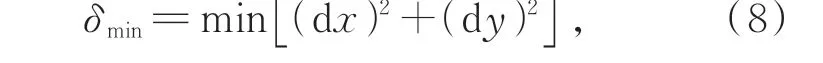
偏移量累计误差最小即为最佳匹配结果。

3.2.2 分镜头图像自适应切分匹配算法

因拍摄环境以及人为因素，相邻分镜头光谱图像重叠率存在差异。为了对不同大小和重叠率的光谱图像实现拼接。提出一种自适应切分匹配算法，针对不同光谱图像动态调整总切分次数及切分步长，在保证拼接质量的同时提高算法自适应性。

由于相位相关法对重叠率高于50%的图像有比较好的拼接效果，为提高算法时间效率，从图像非重叠侧的1/2 处开始切分，则切分步长为：

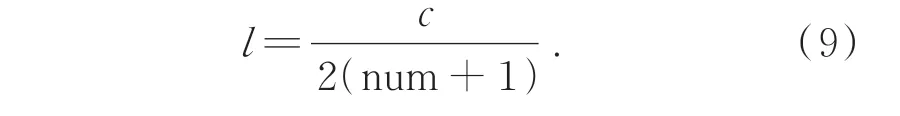
对两张子图像进行相位相关法计算。理想情况下，当两张图片重叠部分完全一致时，其相位相关脉冲函数峰值只有一个。但在实际运算过程中，由于拍摄时光照不均、拍摄角度不一等因素，两张图像重叠部分并非完全相似，故脉冲函数峰值能量四处扩散，出现若干与最大峰值相近峰值，对匹配结果产生干扰。若直接将最大峰值所对应的偏移量作为最终图像偏移量，易导致误匹配。

针对上述问题，取切分后子图像使用相位相关法匹配，寻找脉冲函数阵列中最大峰值max_value，以及与最大峰值相差λ∗max_value以内的其他峰值，将各峰值对应相对偏移量进行存储，作为待验证偏移量。λ为范围参数，其取值根据实际应用场景调整，取值范围为[0.01，0.1]。λ取值越大，拼接准确率越高，但时间成本也会随之增加。因相位相关法计算速度快，为保证拼接质量，本文实验λ取0.1。

为寻找最佳匹配结果，在相位相关性增强拼接算法基础上引入最小二乘法迭代验证自适应调整切分总次数及步长，寻找最佳匹配结果，实现低重叠率壁画光谱图像的拼接。具体步骤如下：

Step1 设初始切分次数num=0，切去的步长数i=0。

Step2 num=num+5。

Step3 对图像进行切分，每次切去一个步长，切去总步长数i=i+1。

Step4 对子图像进行相位相关法匹配，保留不低于最大峰值10%的所有峰值对应偏移量。

Step5 将偏移量所对应的重叠区域再次进行匹配，保留最大峰值对应偏移量为Δx、Δy。若有n组保留下来待验证平移量，可得n组对应的Δx、Δy。

Step6 根据图像重叠区域的高度一致性，在所得n组Δx、Δy中，利用最小二乘法对进行寻优，保留其对应的偏移量x1、y1。

Step7 当i＜num 时，重复Step3，否则执行Step8。

Step8 因光谱图像本身存在噪点，易出现误判，出现位置接近原点峰值，导致Δx2+Δy2的值极小。为使结果更加可靠，取每次切分后所得x1、y1的众数，为总切分次数下的最佳偏移量。

Step9 为提高算法精确度，对切分次数和步长进行自适应调整。对Step8 偏移量对应重叠部分再次验证，当Δx2+Δy2≤ε时，其对应x1、y1即为两幅图像间最终偏移量dx、dy；否则返回Step2 直至找到误差范围内最佳匹配结果。

Step10 利用最终偏移量对图像进行拼接。

因本文方法无需涉及亚像素，实验表明，当ε取值为1 时均能达到较好匹配效果，同时验证了本算法的精确度。

自适应切分算法流程如图3 所示。

图3 自适应切分算法流程图Fig.3 Flow chart of adaptive segmentation algorithm

3.3 多光谱图像拼接与融合处理

多光谱图像各通道所含信息各有差异，研究时需对每个通道进行拼接，将多通道进行融合以增加图像信息量。考虑到匹配效率及个别通道信息量不足等问题，其过程不可简单视为对所有通道逐一配准拼接。此外，单通道拼接时误差各异，导致多通道融合时累计误差较大。故需选取信息量最大波段光谱图像为基准进行匹配运算，利用所得偏移量信息对其余通道定位映射，完成多通道快速拼接［24］。保证各通道误差及拼接后大幅图像维度一致性，降低多通道融合时的累计误差。本文所用多光谱图像通道数为16，若计算出在基准通道下A1、A2 两幅光谱图像偏移量分别为Δx、Δy，则其对应通道的拼接如图4 所示，其中P为图像长度，Q为图像宽度，R为波段数。

图4 多光谱图像A1 和A2 拼接示意图Fig.4 Schematic diagram of multispectral image A1 and A2 splicing

采集过程中光照强度的不同会使两幅图像亮度存在差异，导致配准后图像拼接处存在明显缝隙。为了使图像拼接处过渡自然，需对图像进行融合处理以消除缝隙［25-26］。本文引入加权平均法对两幅图像的重叠部分进行融合处理。设处理后图像灰度值为I(i，j)待拼接图像灰度值分别为I1与I2，则有：

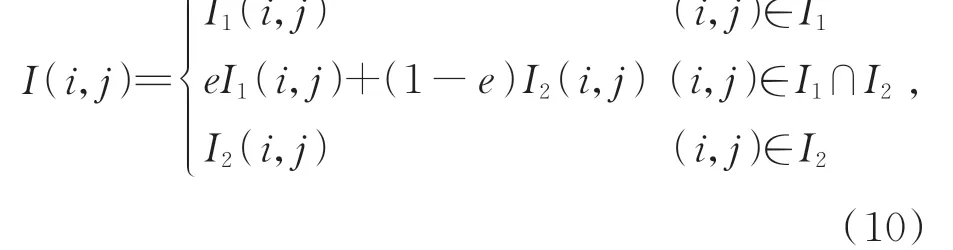
式中，e为权重系数，一般情况下为：

式中，xmax和xmin为两幅图像相同部分在X轴方向上的极大值和极小值。图像的融合可使图像灰度值进行缓慢过渡，消除光照不均对拼接效果造成的影响，实现无缝拼接。

4 实验与结果分析

4.1 算法性能分析

为验证本文算法的有效性与普适性，采用5组不同光谱壁画图像作为实验数据。首先将本文算法与传统相位相关法在图像低重叠率时的拼接有效性进行对比。选取像素大小为1 363×965，重叠率为11.4%的A1、A2 两幅分镜头多光谱壁画图像，使用相位相关法与本文算法进行拼接，结果如图5 所示。

图5 传统相位相关法与本文算法拼接效果对比。（a）待拼接图像；（b）传统相位相关脉冲图；（c）本文算法脉冲图；（d）传统相位相关法拼接结果图；（e）本文算法拼接结果图。Fig. 5 Comparison of stitching effect between traditional phase correlation method and this algorithm.（a）Image to be spliced；（b）Traditional phase correlation pulse diagram；（c）Pulse diagram in this paper；（d）Splicing result diagram of traditional phase correlation method；（e）Stitching results of this algorithm shown in the figure.

由图5 传统相位相关脉冲图像（b）可得，在光谱壁画图像重叠率11.4%，即在重叠率较低情况下，脉冲图出现多处明显尖峰，虽有最大峰值，但峰值能量较低，对应偏移量也存在较大误差。由图5 中本文算法脉冲图像（c）可以看出，本文算法通过对图像进行合理切分，增强图像的相关性，在此基础上进行相位相关法配准，其脉冲图像得到明显改善，存在明显尖峰且相关峰值能量变大。但由于壁画光谱图像本身存在噪声，导致脉冲图像仍存在其他小峰值，因此引入最小二乘法进行偏移量寻优，检测出A1、A2 两幅图像的最优水平及竖直偏移量分别为176 像素、110 像素，并以此作为定位映射标准进行拼接和融合。与传统相位相关法拼接结果（d）相比，本文方法拼接结果（e）无拼接错位误匹配问题，且拼接效果远优于传统相关相位法。

为验证本文所提算法的普适性，分别对剩余4 组大小、重叠率各异的壁画光谱图像利用本文方法进行拼接实验，实验效果如图6 所示。

由图6 可以看出，对于5 组大小、重叠率各异的光谱图像，本文方法均有比较好的拼接效果，其客观指标如表1 所示。

图6 不同壁画光谱图像拼接结果Fig.6 Mosaic results of spectral images of different murals

表1 5 组壁画光谱图像拼接结果Tab.1 Mosaic results of five groups of mural spectral images

由表1 得5 组壁画光谱图像重叠率最低为5%，最高为20.3%，A、B、E 三组壁画光谱图像只需切分5 次即可算出相对偏移量，平均时间成本只需0.411 s。C、D 两组壁画光谱图像合适切分次数为10，平均时间为0.805 s；虽时间成本与切分次数呈正相关，但其拼接时间均在可接受范围内。实验表明，对于大小、重叠率不同的5 组壁画光谱图像，本文所提算法均可找到合适的切分次数，并计算出各图像间最优偏移量，达到低重叠率壁画光谱图像快速无缝拼接的效果。

4.2 多通道光谱图像实验对比分析

对于多通道图像拼接而言，不同通道图像亮度、信息量存在较大差异，对拼接质量也会造成一定的影响。因大幅壁画图像难以获取，为更好地验证本文算法的优越性，对D1 分镜头的520，740，900 nm 通道光谱图像进行分割并重新拼接，将本文算法分别与经典的Harris、SIFT 算法以及最新的FAST-SURF、BRISK-ORB 算法进行比较，实验结果如图7 所示。

由图7 可得，基于特征点检测的SIFT、FAST-SURF、BRISK-ORB 算法在740 nm 通道有较好的拼接效果，Harris 算法拼接结果边缘存在轻微的几何形变，但在低照度通道下，图像亮度比较低，检测到的特征点数量减少，导致拼接误差增大，在520 nm、900 nm 通道图像拼接时，4 种算法均出现了不同程度的几何形变，其中Harris、BRISK-ORB 两种算法的几何变形较严重。本文算法在3 个通道均有比较好的拼接效果，验证了本文算法在图像亮度变化方面相对于其他上算法有较强的鲁棒性。

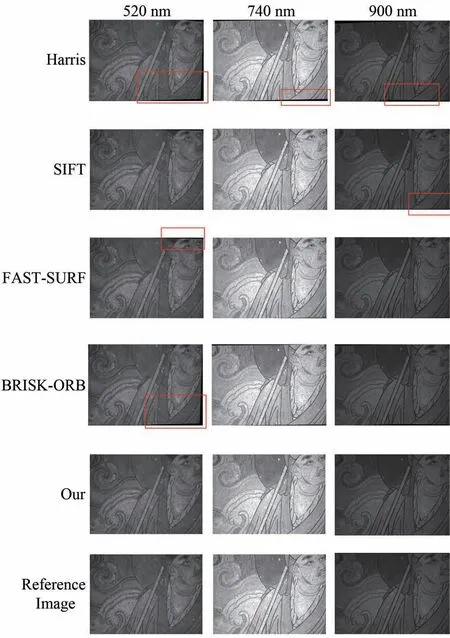
图7 不同算法拼接效果对比图Fig.7 Comparison of splicing effects of different algorithms

以D1 为参考，采用结构相似性（Structural Similarity Index，SSIM）、峰值信噪比（Peak Signal to-Noise Ratio，PSNR）、均方根误差（Root Mean Squard Error，RMSE）3 个全参考评价指标及时间成本对不同算法拼接结果进行评价。其中SSIM 由亮度、对比度、结构对比3 部分组成，其值越大，图像的相似度越高；PSNR 利用两幅图像对应像素之间的误差来评价拼接质量，其值越大，拼接质量越好；RMSE 反映了参考图像与拼接图像之间的偏差，其值越小，表示两幅图像越相近。对比结果如表2 所示。

由 表2 可 得，在740 nm 通 道 下，5 种 算 法 均有较好的拼接效果，本文算法拼接效果略优于其他算法；在520 nm、900 nm 低照度通道下，本文算法在SSIM、PSNR、RMSE 均明显优于其他4 种算法。在4 种对比实验中SIFT、FAST-SURF 拼接效果优于Harris、BRISK-ORB 算法。在拼接时间成本上，本文算法略快于BRISK-ORB 算法，相对于Harris、SIFT、FAST-SURF 三种算法有明显的时间优势。验证了本文算法在多通道光谱图像拼接准确性与时间成本方面有更好的效果。

表2 不同算法拼接结果对比Tab.2 Comparison of stitching results of different algorithms

为了实现多通道光谱图像的快速拼接，选取光谱图像信息量最大通道作为基准通道，获取拼接偏移量后定位映射其余通道，实现多通道图像的快速拼接。图像信息熵反映图像信息的丰富程度，其值越大图片质量越好。图像信息熵公式为：

式中，pi表示灰度值为i的像素在图像中所占的比例，即此灰度值在整幅图像中出现的概率。分别对A1、A2 16 个通道的壁画光谱图像信息熵进行计算，得到各通道图像信息熵曲线如图8所示。

由图8 可得，在400～740 nm 波段，两幅图像信息熵随波长增大而增加，当波长为740 nm 时，两幅图像信息熵最大；在740～940 nm 波段，图像信息熵随波长增大而下降。故实验选择A1、A2的740 nm 波段光谱图像作为基准图像。

图8 A1 和A2 图像的16 个通道信息熵变化图Fig.8 Information entropy change diagram of 16 channels of A1 and A2 images

将本文算法应用于实际16 通道的光谱图像拼接。因无原图像参考，使用信息熵（Information Entropy，IE）、平均梯度（Average Gradient，AG）与总体拼接时间作为评价标准与Harris、SIFT、FAST-SURF、BRISK-ORB 四种算法进行对比。其中平均梯度反映图像中的微小反差和纹理特征变化，其值越大，图像层次越丰富，图像越清晰。实验结果如表3 所示。

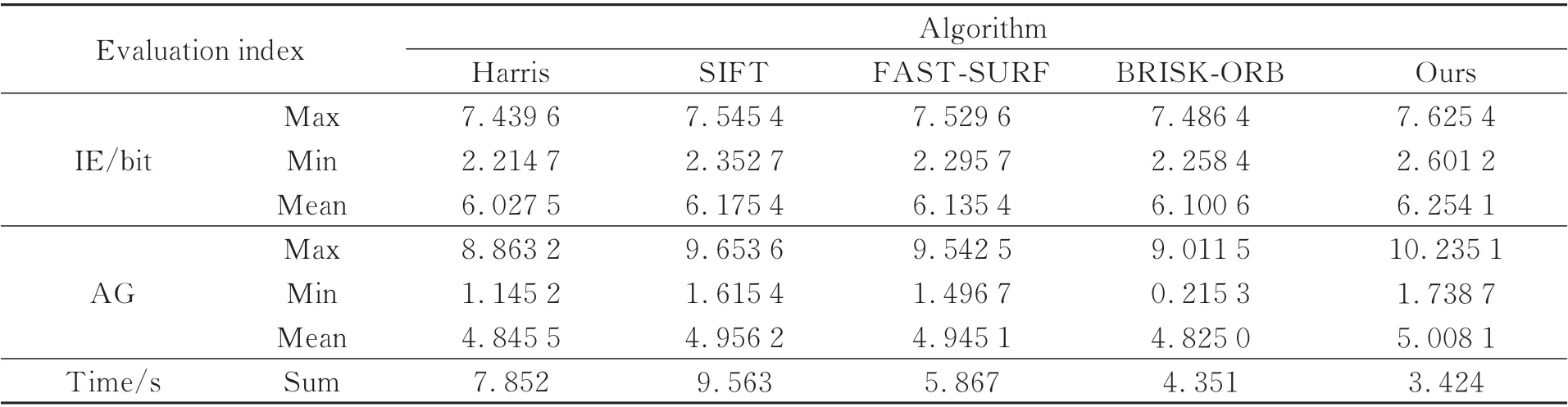
表3 16 通道拼接结果对比Tab.3 Comparison of 16-channel splicing results

由表3 可得，本文算法所得壁画多通道光谱拼接图像信息熵、平均梯度均大于其他4 种算法，拼接效果最优。总体时间成本较其他4 种算法也有比较大的优势，说明了该算法在多通道光谱壁画拼接质量和速度上的优越性，可满足多通道低重叠率光谱图像的快速拼接需求。图9 所示为使用本算法对16 通道光谱图像拼接结果。

图9 16 通道光谱图像拼接效果Fig.9 16 channel spectral image mosaic effect

如图9 所示，本文算法可将基准通道光谱图像对应偏移量进行定位映射，对图像信息量较少通道实现较好拼接，完成多通道低重叠率光谱图像的快速拼接。

5 结 论

本文提出了一种相位相关性增强的自适应低重叠率多通道光谱图像拼接算法。设计了相关性增强图像切分法与相位相关法进行融合；在此基础上引入最小二乘法进行迭代验证，动态调整切分次数与步长进行偏移量寻优，解决了相位相关法在低重叠率时易出现误匹配问题，保证了匹配准确度的同时提高了算法自适应性；通过计算对比各通道图像信息熵，选取最大信息熵通道为基准通道，采用本文算法计算基准通道图像相对偏移量，通过对各通道偏移量定位映射实现了多光谱壁画的多通道快速拼接。在多光谱壁画图像的拼接实验中，实现了重叠率不低于5%多光谱壁画的无缝拼接，且可对多通道光谱图像快速拼接。与主流的拼接算法进行对比，本文算法整体拼接质量与时间成本均优于其他方法，验证了该方法在低重叠率多通道壁画图像拼接方面的有效性与可行性，可为壁画的光谱分析与重建、壁画虚拟修复等研究提供大空间高分辨率数据支持，具有一定的现实意义和实用价值。