依据学情 合理整合
——人教版教材二年级上册“表内乘法”单元整体设计的实践研究
□丁国铣 邵汉民
“表内乘法”是人教版二年级上册一个重要的学习内容,安排了两个单元——表内乘法(一)、表内乘法(二)。教材编排了14个例题,13组练习,共38页,占教材总页数的36.2%。这些内容主要分成三个部分:乘法的初步认识;乘法口诀;解决问题。其中乘法口诀的学习与记忆占很大的比重。我们在实际教学中发现,在学习表内乘法之前,约有80%的学生已经能够按照一定的顺序熟练背诵乘法口诀。基于这样的学情,有必要在照顾零起点学生学习的情况下,把教材编排的乘法口诀与解决问题进行适当整合,以更好地体现乘法含义、计算与应用的一体化,提高课堂教学效率。
一、教材内容与学情分析
(一)梳理学习内容与序列
1.分门别类,明确目标
按照学习内容可以将这两个单元分成三个板块,分别是乘法的初步认识、乘法口诀和用乘法解决问题。表1 呈现的是按这样的分类对学习内容进行的梳理,同时确定了每一个例题需要达成的目标[注:带*号的是表内乘法(二)中的例题]。
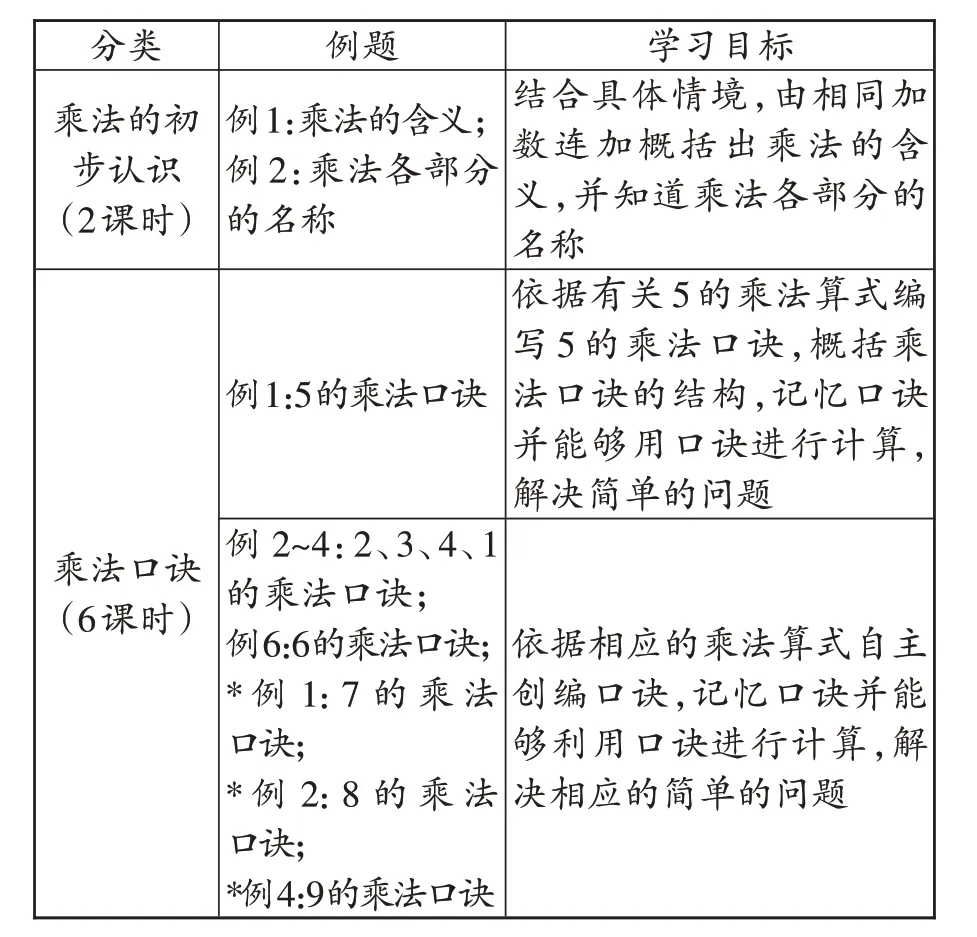
表1

续表
从表1 中可以发现,乘法口诀的学习有6 个课时,占总课时数的一半。除了“5的乘法口诀”需要探究口诀的编写规律外,其余的乘法口诀均可以由学生按照规律自主编写。这里把乘加、乘减也列入解决问题之中,因为它是基于图式形式的列式计算,与“*例5”的基本结构相同。解决问题中的“例7”和“*例3”就乘法解决问题而言,前者可以用“以一当一”的示意图表示,后者则把每份数看成一个整体——“每个铅笔盒8元”,更加抽象。
2.梳理序列,明晰联系
以上三个板块,将乘法口诀的学习与解决问题交替编排,“先算后用”是其基本思路,具体序列如图1所示。

图1
在乘法初步认识的基础上,后两个板块可以分成如虚线框中的三轮。第1轮是学习5以内的乘法口诀,结合图式列出乘法或乘加、乘减的计算题进行计算;第2轮是学习6~8的乘法口诀,依据文字叙述还原图式学习乘法解决问题,并与两数相加的解决问题相区别;第3轮是学习9的乘法口诀,结合图式用乘加、乘减解决问题。显然,每一轮学习均是以乘法口诀作为起点,以解决问题作为具体应用。
(二)学情分析
这样将乘法口诀与解决问题交替进行的学习,客观上拉长了乘法口诀的学习时间,适合处于零起点或低起点认知的学生的学习。然而,对于大部分能够熟练背诵口诀的学生来说,这样小步子交替式的学习,反而不能激发他们学习的积极性。同时,解决问题部分内容也显得较为松散,如“乘加、乘减”与“乘加、乘减解决问题”放在解决问题的开头与结尾,无法很好地体现两个内容的延续性。乘法计算与乘法解决问题分课教学,不能让学生很好地体会“算用结合”的思想。
深入钻研教材,细致了解学情,是进行单元整体设计的基础。通过上述梳理与分析,可以发现“表内乘法”的教材编排与学生学情不相匹配。因此有必要对教材的编排进行合理重构。
二、教材内容的重新建构
我们尝试将乘法口诀的学习与解决问题进行合理整合,即把乘法口诀与解决问题放在同一节课中教学,让少部分没有乘法口诀基础的学生能够按部就班、扎实地学习乘法口诀,而已经能够背诵乘法口诀的学生在复习回顾的基础上,能够在熟练应用中加深对口诀的理解,其中新课与复习课的设计如表2所示。
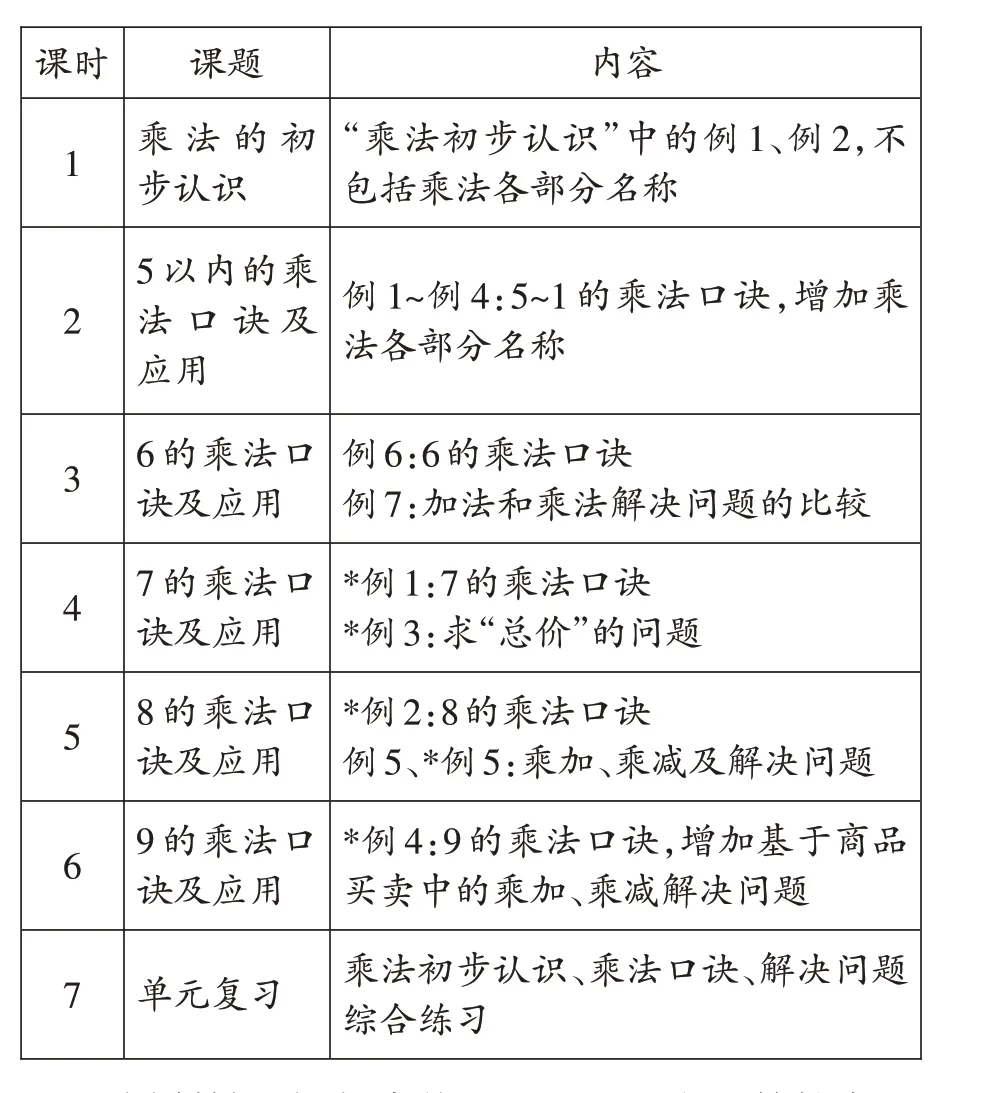
表2
这样的设计,努力体现以下几个方面的特点。
(一)乘法概念学习时注重含义的建构
调查中发现,有很大一部分学生对于乘法口诀的记忆是机械的,并没有真正理解乘法的含义。如学生看到乘法算式“3×5”,只会想到“三五十五”,而并不理解“3×5”的含义。因此,在第1课时教学中,为了让学生尽可能多地结合“数数”与“连加算式”认识乘法的含义,教师可以直接让学生从相同加数连加的算式中数出“几个几相加”,再用乘法表示出来。乘法中“积”的名称的教学放到第2 课时中,在让学生寻找“三五十五”中各个数的含义时,引出“积”。
同时,在乘法含义的学习中,教师基于“认识乘法要从数数开始”这一理解,将“几个几相加”与“几乘几”进行比较沟通,把“数数”分成两类,一类是结合图式直接数数,另一类是数连加算式中相同加数的个数。对数数的结果(几个几相加)进一步数学化,可以让学生更好地理解乘法基本含义。
(二)注重解决问题与口诀学习的融合
将乘法口诀的学习与解决问题同步推进,是本单元整体设计的特色。具体设计每节课时,应遵循先学习乘法口诀,再进行解决问题学习的原则。教师要对解决问题例题中的数据进行适当改编,尽量采用本节课学习的乘法口诀,并在之后的练习中对已经学习的乘法口诀进行复习。如此在不断重复、回顾的过程中,既巩固了乘法口诀的学习,又加深了学生对乘法解决问题的数量关系的认识。
这样的设计压缩了乘法口诀的学习时间,既能让已经会背口诀的学生着重于对口诀含义的理解与乘法口诀之间内在联系的探究,又能让没有乘法口诀基础的学生在学习中经历三个阶段:第一阶段,结合5 的乘法口诀学习乘法口诀的编写原理;第二阶段,利用编写原理进行乘法口诀的创编(这部分内容分为4以内的乘法口诀以及6、7、8、9的乘法口诀,教学序列与人教版教材的编排序列相同);第三阶段,记忆乘法口诀,在直接记忆加数较少的乘法口诀的基础上,寻找其他口诀与这些口诀之间的联系,让零起点学生也能够做到在课内基本记住口诀。
对于解决问题的教学,则可以把它作为乘法含义、乘法口诀的练习与应用,分成两个层次进行:第一层次是用乘法解决问题,这其中又分为一般意义下的乘法解决问题,即“求几个几相加”可以用乘法计算以及初步感悟“单价×数量=总价”这一数量关系。第二层次是用乘加、乘减解决问题,依据乘法解决问题,分别增加新的信息引出相应的乘加、乘减解决问题,体现两类解决问题的结构特征与相互联系。
从以上重构过程可以看出,以整合为基本思路的重构并不是简单的压缩课时,而是基于学情,在可接受原则的指导下进行有机整合,既可以让每一节课都有明确的目标,又可以让不同的学生对于乘法的学习有所收获。
(三)单元复习时注重三者联系
本单元复习综合了“乘法概念、乘法口诀与乘法解决问题”这三部分内容,在分板块复习的基础上,努力构建起三者的联系,即当出现一句乘法口诀时,能够联想到对应的乘法算式;依据乘法算式,利用乘法意义,画出图式或者编制相应的实际问题。同时,还需要从数学文化的角度,介绍“九九乘法口诀”的历史背景,探究乘法口诀中的特点,从中管窥“传统中国文化”。
可以看出,重构的基本策略是“整合”,把“几个几个地数数”“相同加数连加”“乘法含义”进行整合,更加体现乘法的本质特征。把“乘法口诀”与“解决问题”进行整合,体现算用结合的思想。这样的整合,既可以很好地体现乘法的本质,也顺应了学生的学情。
三、单元整合下的教学策略
教师在进行乘法口诀与乘法解决问题整合教学设计时,要顺应学生的思维,突显数学知识的本质,让不同层次的学生均有所得。
(一)从“群数”的视角概括乘法的含义
人教版教材四年级下册中对乘法的定义是这样的:“求几个相同加数的和的简便运算,叫作乘法。”根据这样的表达,由乘法算式直接联想到的是加法算式。把“数数”过程中的几组相同数据进行记录,表示为“几个几相加”,得出乘法算式。如“3+3+3+3+3”表示“5 个3 相加”,用乘法写作“5×3”或“3×5”,其中的“5”,是通过数“相同加数”的个数得到的。因此,把乘法形成的过程与“数数”联系起来,且是“群数”结果的记录,能够帮助学生更直观地理解乘法的含义。
(二)从“联系”的视角记忆乘法口诀
怎样让学生在理解的基础上记忆口诀?怎样增添乘法口诀记忆的趣味性?可引导学生从“联系”的视角,探究同一组乘法口诀中蕴含的积的变化规律;积相同的乘法口诀中蕴含的因数的变化规律;借助故事情节记忆口诀;等等。
(三)从“概念”的视角学习解决问题
乘法解决问题中,学生要经历从依据图式列式到依据文字表述列式的过程。在教学乘法含义与乘法口诀时,可借助直观图式,引导学生由加法含义概括出乘法含义,由加法计算概括出乘法口诀。把图式含义用文字含义进行表达,得到信息与问题,逐步形成解决问题的基本结构。具体地说,在乘法初步认识时,可把图式信息转化成文字信息,初步感知乘法的基本信息;在解决问题时把文字叙述转化成图式表征,建立乘法含义的基本表象;结合具体图式说明乘加或乘减的数量关系。
通过实践研究,笔者认为“表内乘法”的教学可以依据学情进行适当整合,把乘法意义、乘法口诀与乘法解决问题有机融合,形成更加完整的乘法学习结构。

