（六年级）怎样更好地理解圆锥体积的计算方法

□陈选峰

（浙江省临海市哲商小学 317099）

将长方形沿对角线剪开，可得到两个相等的直角三角形，每个直角三角形的面积是长方形面积的二分之一，而直角三角形和长方形分别绕着同一条边旋转一周后得到的圆锥体积却是圆柱的三分之一。怎么理顺这对“矛盾”，帮助学生更好地理解圆锥体积的计算方法？可以采取以下步骤进行教学。

一、复习计算，初悟“矛盾”

1.呈现问题，发现关系

教师出示图1，请学生说一说图中两个长方形的面积关系。学生发现，长方形的宽不变，长扩大2倍，面积扩大2倍。

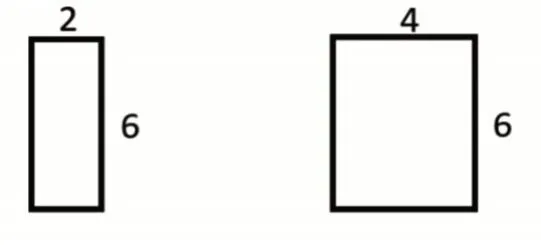
图1

2.借助旋转，初悟“矛盾”

（1）由面及体，感知关系

将图1中的长方形分别以长度为6的边为轴旋转一周，得到两个圆柱（图2）。请学生说一说这两个圆柱的体积有什么关系，为什么。

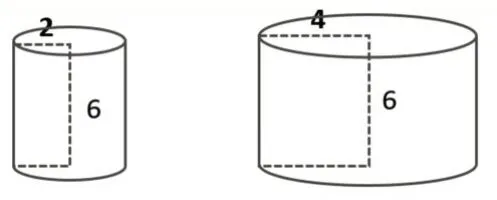
图2

学生发现，长方形的宽不变，长扩大2倍，面积扩大2 倍，以宽为轴旋转一周后，所得的圆柱体积扩大了4倍。

（2）运用想象，感悟“矛盾”

课件演示将图2 的两个圆柱进行叠加得到图3 的过程。请学生想一想：图中①号和②号长方形分别旋转一周，所占的体积谁大？

图3

学生体会到：①号长方形离中心轴远，其旋转所扫过空间的体积大。

二、对比感悟，猜测关系

教师出示图4，请学生先说一说图中三角形与长方形的面积关系，再想一想：图4 中的三角形和长方形分别绕着长度为6的边旋转一周，会得到什么图形？（学生交流后，教师出示图5）接着请学生说一说：图5中圆锥与圆柱有什么相同点？引导发现圆锥与圆柱等底等高。最后请学生猜一猜：等底等高的圆锥与圆柱的体积有什么关系？

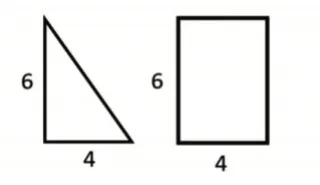
图4

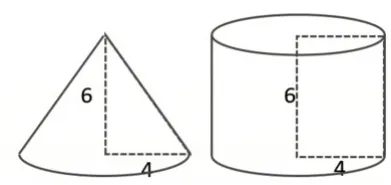
图5

教师将图5中的两个图形进行叠加，得到图6。请学生思考：组成长方形的两个直角三角形有什么关系？圆锥由三角形①旋转而成，三角形②旋转后的空间是哪部分？三角形①和②分别旋转一周，得到的体积谁大？

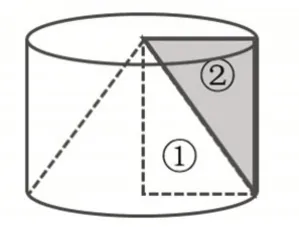
图6

通过交流学生明白，因为三角形②旋转得到的体积大，所以圆锥的体积比等底等高圆柱体积的二分之一要小。

三、实验操作，推导关系

教师引导学生利用等底等高的圆锥与圆柱形容器，进行以下操作。

（1）将圆锥盛满水，倒入圆柱中，观察水占圆柱容器的几分之几。

（2）重复前面的操作，思考圆锥体积与圆柱体积的关系。

之后，引导学生讨论：等底等高的圆锥与圆柱的体积有什么关系？结合学生的回答归纳：圆锥体积是等底等高圆柱体积的三分之一。再让学生思考：根据圆柱体积的计算方法，圆锥的体积可以怎么计算？根据讨论小结：圆锥体积等于底面积乘高乘三分之一。

以上学习过程，通过呈现图形体积关系的演变过程，让学生先从空间维度感知圆锥与圆柱的体积关系，再借助实验操作帮助学生更好地理解了圆锥体积的计算方法。