基于GERG-2008方程对CH4-H2混合物压缩因子的计算与因素分析
王国云,李长俊,贾文龙
(西南石油大学 石油与天然气工程学院,四川 成都 610000)
近年来,氢气(H2)作为公认的清洁能源,得到了越来越多的关注和应用。将H2以一定比例掺入天然气中,然后利用天然气管道或管网进行输送,是实现H2大规模输送的有效方式[1]。荷兰Ameland项目进行了H2摩尔分数为5%~20%的掺氢研究[2];英国HyDeploy项目进行了对现有天然气网络以H2摩尔分数为20%的掺氢量输送的研究[3]。由于H2与甲烷(CH4)物性差异巨大,在标况下两者密度相差达到8倍以上[4-5],且天然气中非烃气体的存在会影响其性质,如压缩因子、密度和焓等[6]。天然气的压缩因子是地面集输工艺和长输工艺所需的重要参数[7]。与常规天然气相比,掺氢天然气中H2摩尔分数会对天然气压缩因子的计算产生重要影响,因此获取掺氢天然气准确的压缩因子,对天然气的混氢输送具有重要意义。
目前石油工业领域一般使用Peng-Robinson(PR)和Soave-Redlich-Kwong(SRK)等方程计算天然气的压缩因子,对该压缩因子的计算主要针对CH4、乙烷和二氧化碳等组分,而组分中H2由于含量较低往往在计算中被忽略[8-9]。关于掺氢天然气压缩因子计算方法的适应性研究尚不够充分。2015年,国际标准化组织天然气技术委员会(ISO/TC 193)发布了采用GERG-2008方程来计算扩展温度和压力范围内的天然气热物性参数的国际标准ISO 20765-2[10-11]。胡敏斐等[12]研究发现,GERG-2004方程在计算CH4-H2混合物的p-v-T特性方面具有明显的优势。也有文献[13]研究证明GERG-2008方程在计算天然气压缩因子方面比其他方法有更好的表现。因此,基于GERG-2008方程,有望对掺氢天然气的压缩因子进行更准确地计算。
针对上述问题,本文采用GERG-2008、PR和SRK方程计算CH4-H2二元混合物在130.00~348.15 K、0.20~111.15 MPa条件下的压缩因子,并基于文献数据对精度进行评价,以筛选出适合于计算掺氢天然气压缩因子的方法。进一步分别分析在管输天然气温度和压力范围下,压力、温度和H2含量(摩尔分数,下同)对压缩因子计算误差的影响。
1 物性计算方法
1.1 GERG-2008状态方程
GERG2008方程由KUNZ等[14]在2012年提出。该模型基于多流体近似理论,以无量纲Helmholtz自由能方程形式表示,通过引入大量的实验数据拟合得到大量的回归系数,使得该方程成为目前天然气物性计算领域内计算精度最高,使用最广泛的方法。适用于包括CH4、N2、H2和Ar等21种天然气组分的混合物物性计算。GERG-2008方程基本形式可表示为式(1)~式(3):
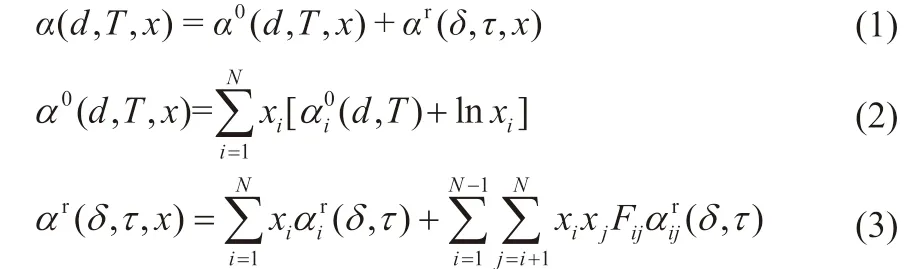
式中,α为无量纲Helmholtz自由能;d为摩尔密度,mol/L;T为温度,K;x为组分摩尔分数;α0为理想Helmholtz自由能;αr为Helmholtz自由能余相;xi为第i组分摩尔分数;δ为对比密度;τ为对比温度的倒数;Fij为调节系数,等同于一个专门的偏离函数;表示偏离函数。
混合物的对比密度(δ)和对比温度的倒数(τ)由减函数求得,基本形式分别如式(4)和式(5):

式中,i,j分别为两组分;xj为第j组分摩尔分数;dc,i为第i组分的临界摩尔密度,mol/L;dc,j为第j组分的临界摩尔密度,mol/L;Tc,i为第i组分的临界温度,K;Tc,j为第j组分的临界温度,K;βV,ij、γV,ij、βT,ij、γT,ij为二元交互参数,可通过查ISO20765获得[11]。
采用GERG-2008方程计算掺氢天然气的计算压缩因子(Z)所需方程如下(参数和指数可通过查ISO20765获得[11]):
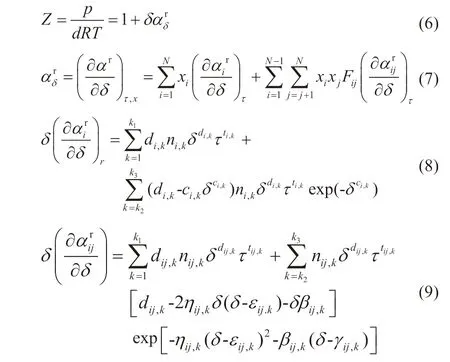
式中,p为绝对压力,Pa;R为气体常数,8.314472 J/(mol·K);di,k、ni,k、di,k、ti,k、ci,k、dij,k、nij,k、ηij,k、tij,k、εij,k、βij,k、γij,k为系数和指数,其值在ISO 20765-2中给出[11]。
求解压缩因子计算步骤如图1所示。
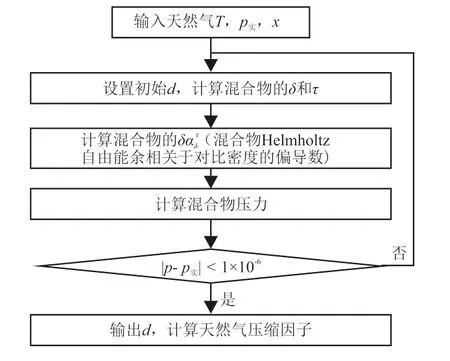
图1 GERG-2008方程压缩因子计算步骤Fig. 1 Calculation steps of compression factor of GERG-2008 equation
1.2 其他计算方法
SOAVE[15]于1972年提出了RK方程的改进式:SRK方程。SRK方程不仅具有如RK方程形式简单的优点,还大大改善了计算气相和液相逸度的效果,对CH4-H2混合物压缩因子进行计算的SRK方程如式(10)~式(12):
式中,a和b为与混合物所含组分的种类及状态有关的常量。
PENG等[16]于1976年提出了立方型状态方程:PR状态方程。通过状态方程的引力项选择适当的函数形式,使临界压缩因子的预测值更接近于真实值,是石油化工工业常用的热力学方程之一,其压缩因子计算式如式(13)(系数与SRK方程相同):
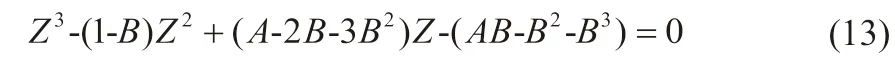
2 计算结果及讨论
2.1 CH4-H2混合物压缩因子实验数据
为了评估GERG-2008方程计算CH4-H2混合物压缩因子的准确性,研究者用实验的方法对不同气体样品的压缩因子进行了测试,包括SHIGERU等[17]的压缩因子实验数据、CHUANG等[18]的密度实验数据和MACHADO等[19]的比容实验数据。采用式(6)将密度和比容实验数据转换为压缩因子实验数据,如表1所示。由表1可知,实验温度范围为130.00~348.15 K,压力范围为0.25~111.20 MPa,H2组分摩尔分数(x(H2))为0.0000~1.0000。

表1 CH4-H2混合物压缩因子实验数据Table 1 Experimental data of compressibility factor of CH4-H2 mixture
2.2 PR、SRK和GERG-2008状态方程比较
运用PR、SRK和GERG-2008方程对不同配比的CH4-H2混合物在实验压力和温度条件下的压缩因子进行了计算,并将计算结果与实验数据进行了对比分析。
压缩因子实验值和计算值之间的相对偏差(RD)和平均相对偏差(ARD)计算方法分别如式(14)和式(15):

式中,Zcal为压缩因子计算值;Zexp为压缩因子实验值;Zcal,i为第i个温度和压力条件下的压缩因子计算值;Zexp,i为第i个温度和压力条件下的压缩因子实验值。
计算得到各模型的CH4-H2混合物的压缩因子的最大相对偏差和平均相对偏差如表2所示。由表2可知,GERG-2008方程压缩因子计算值与实验值吻合较好,其平均相对偏差仅为0.53%,而PR和SRK方程平均绝对偏差分别为3.06%和1.24%;GERG-2008方程计算精度较PR方程和SRK方程分别提高了2.53%和0.71%。
在计算CH4压缩因子时,GERG-2008方程的平均偏差≤ 0.31%,显著优于PR方程和SRK方程。计算H2压缩因子时,当温度高于159.20 K时,GERG-2008方程的平均相对偏差≤ 0.14%;当温度低于159.20 K时,GERG-2008方程的平均相对偏差显著上升,但仍≤ 2.78%,并显著优于PR方程和SRK方程。
在计算CH4-H2混合物压缩因子时,GERG-2008方程最大相对偏差为6.33%,可能是由数据异常引起的。当温度高于273.15 K时,GERG-2008方程平均相对偏差≤0.66%,其计算精度要显著优于PR方程和SRK方程。当温度低于273.15 K时,GERG-2008仍具有较高精度,其平均相对偏差≤2.31%。
通过以上将计算结果与实验数据对比发现,在温度范围为130.00~348.15 K范围内,GERG-2008方程可作为理想的掺氢天然气压缩因子计算方法。由表2可知,温度和x(H2)会影响计算偏差,而在压缩因子计算中,压力也是一个重要的参数。因此进一步分析在管输天然气温度和压力条件下,温度、压力和x(H2)对计算精度的影响。
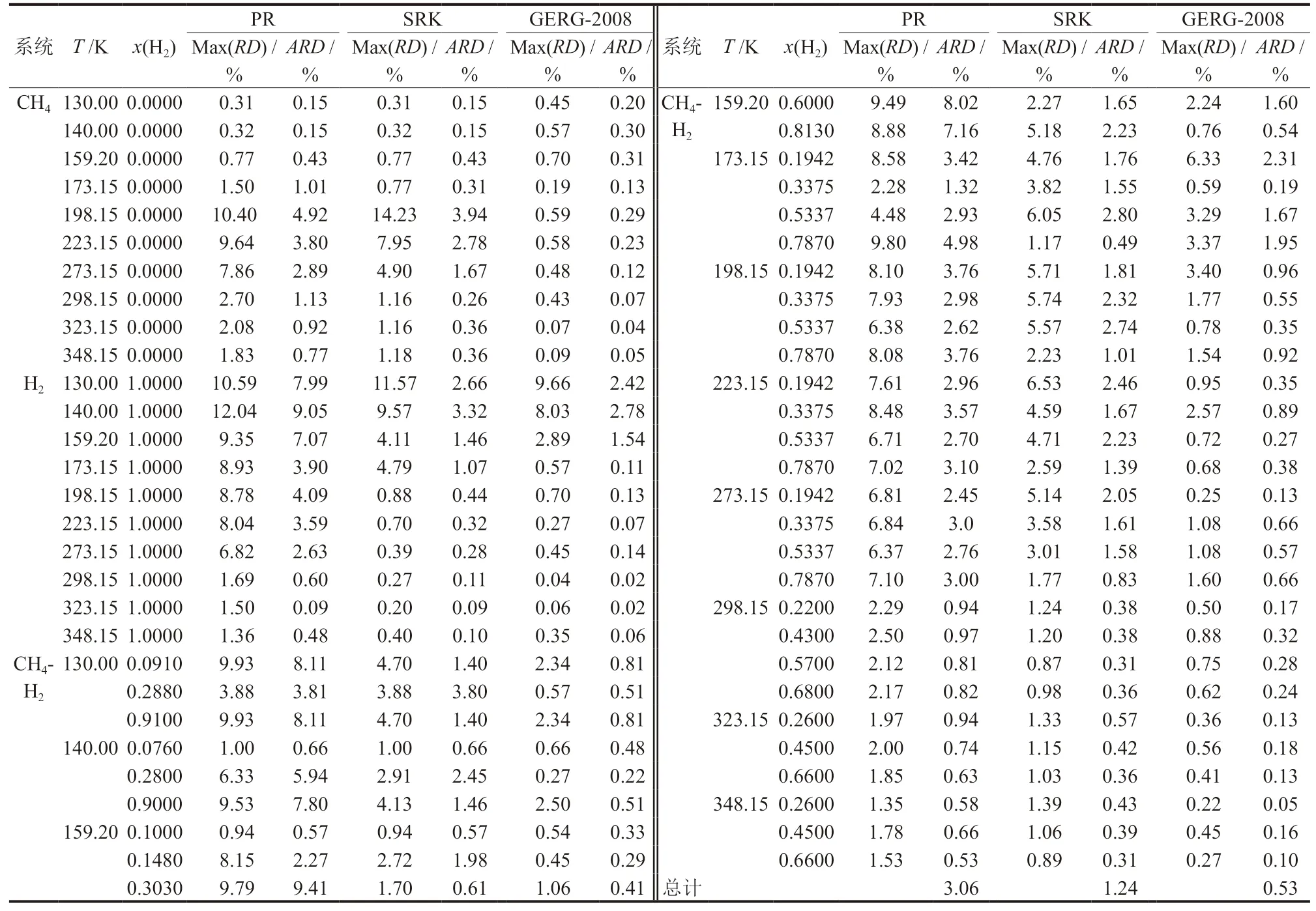
表2 3种模型计算偏差Table 2 Calculation deviation of three models
2.3 误差影响分析
2.3.1 压力影响分析
为了契合实际应用需要,考虑到管输天然气的压力一般在0.00~12.00 MPa范围内,温度在263.00~338.00 K范围内。采用GERG-2008方程对不同配比的CH4-H2二元混合物,在273.15 K、298.15 K条件下的压缩因子进行了计算。将GERG-2008方程计算的相对偏差与PR方程和SRK方程计算的相对偏差相比较,结果如图2和图3所示。

图2 压力对压缩因子相对偏差的影响Fig. 2 Effect of pressure on RD of compressibility factor
由 图2(a)可 知,当x(H2)为0.2200时,采 用GERG-2008方程与PR方程和SRK方程计算的相对偏差变化趋势相同,相对偏差均随着压力的增大而增大,PR方程增加的最快,SRK方程次之,GERG-2008方程增加最慢。图2(b)也验证了这一点,当压力小于12.00 MPa时,其相对偏差均随压力的增大而增大。由图3(a)可知,当压力小于10.00 MPa时,采用GERG-2008方程计算CH4和H2的压缩因子时,其相对偏差几乎不受压力的影响;而计算CH4-H2二元混合物时,其相对偏差随压力的增大而增大。图3(b)也验证了这一点,在低压的情况下,其相对偏差均随压力的增大而增大。

图3 GERG-2008方程计算结果Fig. 3 Calculation results of GERG-2008 equation
2.3.2 温度影响分析
采用GERG2008、PR和SRK方程分别计算了不同温度下的压缩因子偏差,结果如图4所示。由图4(a)可知,GERG-2008和PR方程平均相对偏差随温度的升高而减小;SRK方程的平均相对偏差基本不受温度变化的影响。由图4(b)可知,当温度低于273.15 K时,GERG-2008和PR方程平均相对偏差仍随温度的升高而减小。
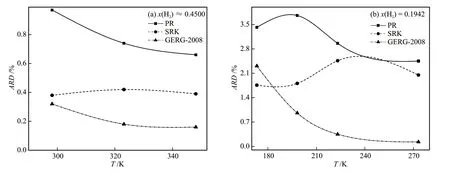
图4 温度对压缩因子平均相对偏差的影响Fig. 4 Effect of temperature on ARD of compressibility factor
2.3.3 H2含量影响分析
在273.15 K和298.15 K条件下,采用GERG-2008方程对不同配比CH4-H2二元混合物、H2和CH4的压缩因子进行了计算。将GERG-2008方程的平均相对偏差与PR和SRK方程的计算偏差相比较,结果如图5所示。

图5 x(H2)对压缩因子平均相对偏差的影响Fig. 5 Effect of x(H2) on ARD of compressibility factor
由图5(a)可知,在298.15K时,SRK和GERG-2008方程变化趋势基本相同,随H2含量的增大,压缩因子的平均相对偏差先增大后减小;而PR方程随H2含量的增大,压缩因子的平均相对偏差逐渐减小。图5(b)中也表明随H2含量的增大,SRK和GERG-2008方程压缩因子的平均相对偏差先增大后减小。在H2含量为0.0000~1.0000范围内,GERG-2008方程的计算精度明显优于SRK方程和PR方程。
3 结论
采用GERG-2008、PR和SRK方程计算了不同配比的CH4-H2二元混合物在不同温度和压力条件下的压缩因子,并将计算结果与文献中的实验数据进行了比较,得到如下结论。
(1)在本文研究范围内,温度为130.00~348.15 K、压力为0.20~111.15 MPa的条件下,GERG-2008方程的计算结果与实验数据平均相对偏差基本在0.53%范围内,较PR和SRK方程的计算精度明显提高,可作为的掺氢天然气的理想压缩因子计算公式。
(2)在管输天然气温度和压力条件下,PR、SRK和GERG-2008的相对偏差均随压力增大而增大,但GERG-2008方程相对偏差的增加幅度明显小于PR和SRK方程。在高压条件下,GERG-2008方程仍然具有较高的计算精度。
(3)在173.15~348.15 K范围内,GERG-2008方程平均相对偏差随温度的升高而减小,且在低温条件下降幅越明显;PR方程平均相对偏差也随温度上升而减小。
(4)在管输天然气温度条件下,随H2含量的增大,SRK和GERG方程的平均相对偏差均先增大后减小;在计算CH4和H2压缩因子时,GERG-2008方程相对偏差接近于0。因此,有望通过优化CH4-H2的二元参数,提升GERG-2008方程计算掺氢天然气压缩因子的精度。

