基于集合和神经网络架构搜索的自动历史拟合方法
张黎明, 陈昕晟, 李国欣, 马小鹏, 张 凯,谷建伟, 姚 军, 王 健, 孙 海
(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.中石油勘探与生产分公司,北京 100007; 3.中国石油大学(华东)理学院,山东青岛 266580)
自动历史拟合是以油藏生产系统作为研究对象,通过调整地质模型参数来拟合实际生产动态数据,是进一步了解油藏地下流体分布、预测油藏未来动态、进行油田开发方案部署的重要手段[1-3]。随着油气田开发数字化智能化的不断推进,生产决策对油气藏数值建模的精度要求越来越高[4-7]。另外,由于储层流动机制复杂非线性强,油藏数值模拟计算耗时通常需要数十分钟乃至数小时,导致自动历史拟合是一个高维、求解难度大、计算耗时长的反问题[8-11]。近20年来,尽管已有大量文献研究来提高计算效率[12-18],但根据动态数据反演调整储层模型仍然是一项艰巨的任务。现今自动历史拟合技术在与深度学习方法相交融的过程中逐渐换发出更大的生机,其中的模型参数化[19-21]、优化求解[22]、代理模型[23]等方面为深度学习方法应用的热点领域。尽管训练模型网络参数的设置会对深度学习算法的效果产生一定影响,但是用于选取超参数的超参数优化(hyperparameter optimization,HO)则是决定应用深度学习算法效果好坏的更为重要的因素。训练参数与用于定义网格结构的参数是目前深度学习领域的两类超参数,相较于训练参数,用于定义网格结构的参数具有更高的离散度和维度,且参数与参数之间相互依赖,因此用于定义网格结构的参数的自动调优一般不再划入超参数优化的范畴,而将其定义为网络架构搜索[24-30](neural architecture search,NAS)。网络架构搜索一般按照定义搜索空间、优选搜索策略、搜寻候选网络结构、网络结构评估、结果反馈与深度搜索的流程进行处理,其从本质上来说属于高维空间的最优参数搜索问题。笔者选用进化算法作为搜索策略用于实现网络架构搜索,进化算法选取目前得到广泛应用的粒子群算法[31](PSO),并与深度自编码[32]方法相结合实现对复杂地质模型的特征提取以及降维分解,经过PSO优化后的深度模型能够更好的对地质特征压缩的同时保留足够的信息实现保持与复杂地质特征一致的油藏模型重构。结合降维后的低维空间连续特征与数据光滑多次数据同化方法进行高效的自动历史拟合反演求解。
1 方 法
1.1 自动历史拟合数学模型
油藏的自动历史拟合是利用已知的观测数据来得到油藏数值模型的地质参数,属于典型的反问题,因此需要建立油藏数值模型的地质参数与观测数据之间的数学模型,
dobs=g(m)+ε.
(1)
式中,dobs为生产动态数据;g(m)为油藏数值模拟器;m为地质参数;ε观测数据误差。
基于贝叶斯理论,观测数据与油藏模型参数之间关系式为
(2)
式中,f(m|dobs)为贝叶斯理论中的后验概率,后验概率的数值代表着预测模型逼近真实模型的可能性。
基于假设的模型参数所得到预测数距与观测数据之间的拟合误差即是通过式(2)中的似然函数f(dobs|m)进行量化,而模型的已知参数则以先验概率f(m)进行表示。
观测数据在给定的地质参数m下会存在符合高斯分布的观测误差,即ε~N(0,CD)。其中,CD为协方差矩阵,可得到似然函数f(dobs|m)为
f(dobs|m)∝
(3)
为了求得先验概率,须利用已知的油藏信息建立先验油藏模型mi(i=1,2,…,Ne),可计算得先验模型均值mpr,结合高斯概率模型建立油藏模型参数的先验概率表达式为
(4)
式中,CM为先验模型参数的协方差矩阵。
结合式(4)可得后验概率分布为
(5)
尽管本文中讨论的参数化方法可用于基于卡尔曼滤波的任何方法,但重点关注由Reynolds和Emerick提出的ES-MDA方法,该方法属于一种基于集合的历史拟合方法。ES-MDA方法基于集合模型参数与模拟数据的相关性信息迭代更新求解模型参数,油藏模型参数的估计公式为
j=1,…,Ne.
(6)
式中,CMD为模型参数和预测数据之间的交叉协方差矩阵;CDD为预测数据的协方差矩阵;j为集合中第j个个体;k为迭代次数;αk为膨胀因子。
该方法通过利用一个膨胀因子α和观测数据误差的协方差矩阵CD多次迭代重复数据同化,使算法更新过程更加平稳,以此来改善使用集合卡尔曼滤波方法的缺陷。使用ES-MDA方法,需要首先选择同化迭代次数Na。此外,必须要选择膨胀因子αk,且要满足条件:
(7)
1.2 深度自动编码器
由于储层地质特征的复杂性,往往需要足够精细的网格构建储层数值模型,导致自动历史拟合需要调整的参数通常达数百万,而且河流相等非连续性模型参数具有很强的非线性和非高斯分布,很难知道应该提取什么样的特征。近年来,为了解决上述问题,深度学习方法在自动历史拟合领域获得广泛关注,因为能够从图像中提取相关的、非冗余的和非线性的特征。

深度自动编码器(deep autoencoder,DAE)相对于原始的自编码模型加大了深度,提高学习能力,更有利于预训练。图1为深度自编码模型的结构示意图。首先通过编码器对初始油藏模型进行训练与降维处理,随即得到代表油藏模型低维表征的隐藏层h,将其输入到解码器进行解码重构处理从而得到对应的油藏模型。隐藏层层数与每个隐藏层神经元个数是DAE模型所需要确定的两类超参数。

图1 深度自编码模型结构示意图Fig.1 Schematic diagram of deep autoencoder
1.3 粒子群优化算法
本质上网络架构搜索和围棋类似,是高维空间的最优参数搜索问题。本文中提出采用进化算法中的粒子群算法针对深度自编码模型中的各隐藏层节点数进行网络架构优化。
Eberhart和Kennedy通过研究鸟群觅食行为于1995年提出了粒子群算法(particle swarm optimization,PSO)[31]。PSO算法流程:PSO算法将模型的解抽象为具有速度和位置的粒子,速度和位置分别代表着粒子的移动的快慢和移动的方向。PSO算法首先以一群随机粒子作为初始种群,而种群中的每个粒子将会在N维搜索空间中以一定速度移动到下一个位置,对应优化问题的候选解则与粒子当前的位置一一对应,在搜索最优位置的过程中,算法可以根据种群历史最优位置与粒子历史最优位置动态调整粒子速度。粒子的速度和位置更新公式为
vi=vi+c1Xrand(pi-xi)+c2Xrand(gi-xi),
(8)
xi=xi+vi.
(9)
式中,i=1,2,…,N,N为此群中粒子的总数;vi为粒子速度;Xrand为介于(0,1)之间的随机数;pi为个体最优值;gi为群体最优值;xi为粒子的当前位置;c1和c2为学习因子,通常c1=c2=2。
个体极值即种群中每个粒子在单独搜寻中所找到的最优解,而全局最优解则是种群中最优的个体极值,通过持续地迭代计算,不断地更新粒子群中每个粒子的速度和位置,当到达终止条件后即可得到相应的最优解。
将深度自编码模型网络各层节点个数xi作为PSO算法的优化参数,模型训练后的训练误差作为优化目标函数,利用优化后得到的结果作为隐层节点数组合训练深度自编码模型。
1.4 基于集合和优化深度学习降维重构的历史拟合流程
基于集合和优化深度学习降维重构的历史拟合流程如图2所示。整个流程包括深度自编码器训练部分和自动历史拟合部分。首先对深度自编码器进行结构超参数优选及训练。通过生成的先验地质模型训练深度自动编码器,之后结合粒子群算法优化出深度自编码网络的最优隐层节点数组合,再利用得出的最优组合训练深度自编码网络模型,并将编码器用于油藏模型的参数降维化表征。降维后的参数(即编码器的输出)作为历史拟合的模型参数变量,进行模型反演求解。使用ES-MDA方法的模型更新公式结合观测数据进行迭代更新,利用更新得到的数据通过解码器进行重构求解得到相应的油藏模型,基于该油藏模型进行数值模拟计算得到用于下一步迭代更新的模型数据,计算历史拟合目标函数,判断终止条件。通过不断地按照上述流程进行迭代计算直到满足收敛条件得到最优解,从而进一步输出历史拟合反演得到的油藏模型。
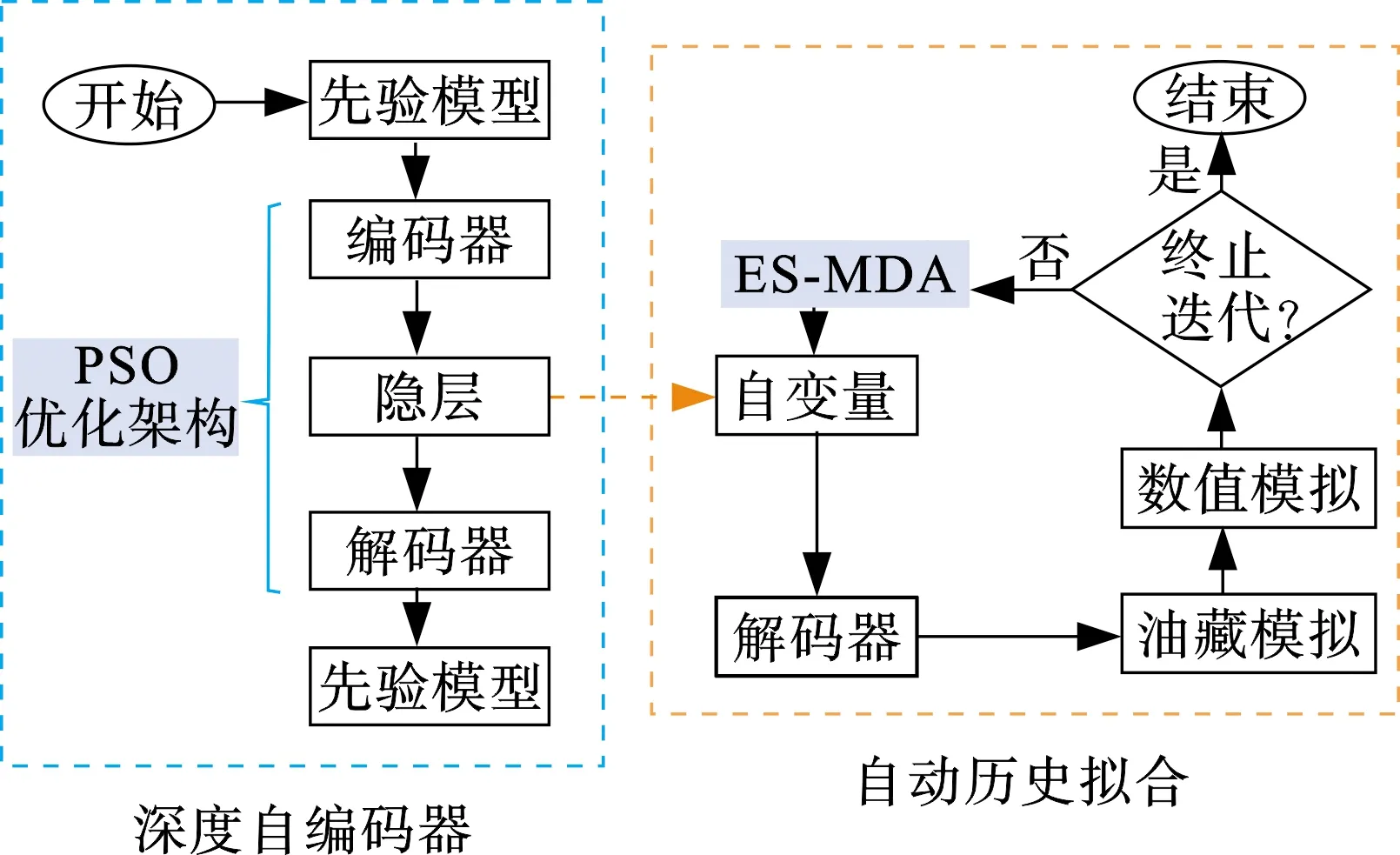
图2 基于集合和深度自编码模型的综合 自动历史拟合流程Fig.2 A comprehensive automatic history matching frame work based on ensemble and deep autoencoder
2 实例应用
2.1 20×20小模型自动历史拟合
该油藏模型是油水两相的水驱油藏算例,通过优化深度学习降维重构参数的方法进行历史拟合研究。油藏数值模拟器选择Eclipse数值模拟软件,该油藏模型拥有多条高渗导流通道,故渗透率为该模型中所需反演的主要地质参数。图3为真实渗透率场,将其作为训练图像。根据训练图像采用多点地质统计方法随机生成20 000个先验模型,取部分如图4所示,高渗区与低渗区之间存在明显相边界,该油藏有20×20个网格,每个网格100 m×100 m,厚度为20 m。1口注水井,4口生产井,采用五点井网进行生产。共3 600 d 18个时间步进行历史拟合测试。

图3 河流相油藏算例真实油藏模型Fig.3 Reference modelof case study of a 2-D fluvial reservoir

图4 河流相油藏算例随机初始油藏模型集合Fig.4 Initial models of case study of a 2-D fluvial reservoir
2.1.1 PSO优化DAE神经网络架构
通过DAE方法训练自编码模型,使用解码器进行降维参数化表征,利用PSO优化算法优化自编码模型的神经网络架构:通过PSO算法针对自编码模型中个隐藏层的节点个数进行优化,粒子群种群数设为20,迭代10次,以表1中参数设置粒子优化范围,神经网络训练迭代次数设为200次,使用20 000个先验随机油藏模型中15 000个模型作为训练样本,另外5 000个模型作为验证样本对模型进行训练。调整神经网络结构,提升网络特征提取能力,改善降维效果。
3种不同隐层节点数的DAE模型在优化前后生成的渗透率场的效果如图5所示。隐层节点数为175-14时的模型重构结果为整体优化的最优结果,而如图5所示,在优化过程中随机选取的两个隐层节点数135-34与155-2的模型重构精度要明显低于前者。图5(a)与(b)由于降维程度过高或过低而导致河流相边界不清晰,重构精度较差,反之,经过合适的降维处理,图5(c)所生成的渗透率场具有良好的重构精度。

表1 深度自编码模型结构

图5 不同隐层节点数的DAE模型在优化前后重构渗透率场效果对比Fig.5 Comparison of permeability reconstruction between DAE models of different numbers of hidden layer nodes with optimization and without optimization
2.1.2 自动历史拟合测试
将ES-MDA与优化前、后的最优结构的DAE(即隐层节点为175-14的DAE模型)相互结合进行历史拟合反演,并将反演结果与使用传统的ES-MDA算法对同一地质渗透率模型进行反演计算得到的反演结果进行对比,图6即为使用3种不同反演方法所得到的前5个反演渗透率场。将ES-MDA算法与SVD方法相互结合进行历史拟合反演得到的渗透率场如图6(a)所示,使用SVD方法降维对河流相进行粗略描绘,无法准确预测出河流相的分布。如图6(b)所示,使用优化前的DAE模型进行降维处理得到的模型的存在河流相边界粗糙以及明显遗漏高渗相区等问题,难以反演得到与真实渗透率场相近的重构模型。而图6(c)中所展示的与真实渗透率场符合度更高的重构模型是通过优化后的DAE模型与ES-MDA方法相结合进行历史拟合所得到的。由此可知,通过将优化后的DAE模型与ES-MDA相结合能够得到更精确的历史拟合反演结果,也能够预测出准确的油藏模型的渗透率分布。
图7为使用优化后的DAE模型结合ES-MDA进行历史拟合的4口生产井的日产油量曲线。由此可知,将PSO-DEA与ES-MDA相结合的自动历史拟合方法反演得到的油藏模型的生产曲线要比初始油藏模型得到的生产曲线与观测数据有更高的拟合度,验证了该方法用于历史拟合反演的可行性与有效性。

图6 前5个自动历史拟合渗透率场反演结果对比Fig.6 Comparison of the first 5 permeability inversion results
2.2 SPE-10模型自动历史拟合
取SPE-10油藏模型中的一层进行优化深度学习降维重构参数的历史拟合。油藏数值模拟器选择Eclipse数值模拟软件。该油藏为连续相油藏,需要反演调整的地质参数为渗透率。图8(a)为真实渗透率场,将其作为训练图像。根据训练图像采用多点地质统计方法随机生成5 000个先验模型,取部分如图8(b)所示。该油藏为有220×60个网格,每个网格100 m×100 m,厚度为20 m。1口注水井,4口生产井,采用五点井网进行生产。共3 600 d 18个时间步进行历史拟合测试。

图8 SPE-10单层油藏算例Fig.8 Case study of a SPE-10 single-layer reservoir
2.2.1 PSO优化DAE神经网络架构
通过DAE方法训练自编码模型,使用解码器进行降维参数化表征,利用PSO优化算法优化自编码模型的神经网络架构。通过PSO算法针对自编码模型中个隐藏层的节点个数进行优化,粒子群种群数设为20,迭代10次,以表2中参数设置粒子优化范围,神经网络训练迭代次数设为200次,以7∶3的比例随机从5 000个先验模型选取油藏模型分别作为训练样本与验证样本进行模型训练,调整神经网络架构,提升网络特征提取能力,改善降维效果。
同时,由于模型维数较高,DAE模型训练较慢,为减少PSO优化所耗费的时间。在前7次迭代时只进行初步训练,即神经网络训练迭代次数设为50次,从第8次迭代开始进行完整的训练过程。

表2 自编码模型结构
随机选取优化前后的一个粒子的参数对深度自编码模型重构结果进行分析,如图9所示。可以看出优化前的自编码模型重构出来的图像较为模糊,重构精度较差,而且隐藏层的维数也较高。优化后的自编码模型重构出来的高渗相的分布趋势能够得到较好地展现,且降维后隐藏层维数更小,重构效果更好。

图9 DAE模型在优化前后重构渗透率场效果对比Fig.9 Comparison of permeability reconstruction between DAE models with optimization and without optimization
2.2.2 自动历史拟合测试
将ES-MDA与优化前、后的最优结构的DAE(即隐层节点为3905-256-41的DAE模型)相互结合进行历史拟合反演,并将反演结果与使用传统的ES-MDA算法对同一地质渗透率模型进行反演计算得到的反演结果进行对比,图10即为使用3种不同反演方法所得到的前5个反演渗透率场。真实渗透率场与使用这两种方法历史拟合反演得到重构渗透率场存在很大的差异,表明这两种方法难以对油藏模型的渗透率分布进行准确预测。图10(c)中相较于前述二者与真实渗透率场吻合度更高的重构渗透率场是通过将优化后的DAE模型与ES-MDA算法相结合进行历史拟合所得到的。由此可知,通过将优化后的DAE模型与ES-MDA相结合能够得到更精确的历史拟合反演结果,也能够预测出准确的油藏模型的渗透率分布。
图11为使用优化后的DAE模型结合ES-MDA进行历史拟合的生产曲线拟合结果。初始油藏数值模型经数值模拟计算所得到的预测结果结合在图中则以多组虚线表示,而更新后的油藏数值模型经数值模拟计算所得到预测数据集合则采用红色实线进行表示。由此可知,将PSO-DAE与ES-MDA相结合的自动历史拟合方法反演得到的油藏模型的生产曲线要比初始油藏模型得到的生产曲线与观测数据有更高的拟合度,验证了该方法用于历史拟合反演的可行性与有效性。
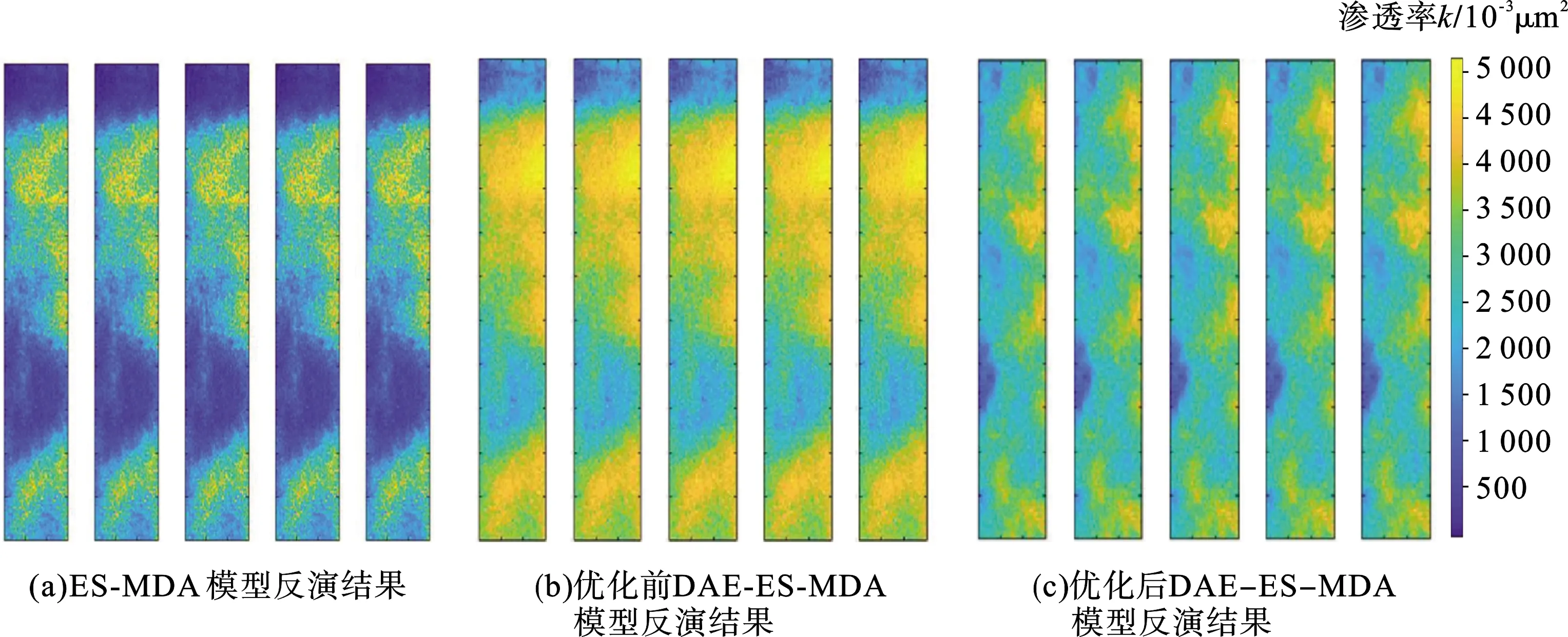
图10 前5个自动历史拟合渗透率场反演结果对比Fig.10 Comparison of the first 5 permeability inversion results

图11 将PSO-DAE与ES-MDA相互结合的方法生产观测数据拟合结果Fig.11 Observed data history-matched results of ES-MDA combined PSO-DAE method
3 结 论
(1)提出了一种新颖的PSO算法,以自动发现用于图像分类问题的深度自动编码器的最佳网络架构,而无需人工干预,同时在优化过程中为了减少所耗时间,采用了优化前期神经网络只进行初步训练的策略。该方法搜索出的最优网络架构的自动编码器能够在保证降维重构精度的基础上对数据降低更多的维度从而占用更少的计算资源。
(2)使用最优体系结构的DAE来对地质模型进行参数化,并结合ES-MDA将这些模型用于油藏自动历史拟合。在地质模型的重构方面,经过所提出的方法优化后的DAE模型明显优于优化前DAE模型参数化所获得的结果,经过自动历史拟合后的反演得结果有显著提升,反演得到的渗透率场更加接近真实的渗透率场。

