基于综合性能指标的控压钻井过程多变量协调控制
孟卓然, 徐宝昌, 罗雄麟
(中国石油大学(北京)信息科学与工程学院,北京 102249)
石油资源的开发和利用正逐步走向深部复杂地层[1]。钻遇高压盐水层、高压裂缝性地层等安全窗口小于0.2 MPa的复杂地层时,常规井筒压力控制方法存在控制精度低,钻进时效差等技术瓶颈。为解决窄压力窗口安全钻井问题,国内外学者们对控压钻井(managed pressure drilling, MPD)技术中井筒压力控制方法进行了广泛的研究。国外深井压力控制技术的研究起步较早,自2008年起开始关注基于模型的先进控制算法与最优估计算法[2-3],以提高井筒压力控制的精度和可靠性。随着设计方法及控制技术的不断进步,2014年以后美国Weatherford公司明确提出在MPD装置中应用智能控制器,但其核心控制算法未见公开[4]。2013年以后,中石油工程院研制的首套PCDS精细控压钻井系统投入使用[5];2016年中国石油大学(北京)、中石油工程院在原有系统的基础上研制出更小规模、更加便捷的单通道控压钻井系统,但其控制算法仍以比例积分微分(PID)控制为主[6]。随着自动化、智能化的快速发展,将钻井自动化操作系统与MPD系统相结合可以实现钻井时效的整体优化。笔者针对以单一节流阀开度为操控变量,井底压力为被控变量的传统控制系统设计思路与现有PID控制方法,提出一种综合多性能指标的控压钻井过程协调控制方法,建立控压钻井过程全局模型并分析井底压力、机械钻速、回压、泵流量、转速、钻压等多源变量间的耦合关系;根据提出的全局模型与综合性能指标,优选井底压差与机械钻速为被控变量,回压、转速、泵流量为操控变量进而设计非线性模型预测控制器。
1 控压钻井过程全局模型
将环空压力预测模型、钻柱动力学模型、机械钻速模型等单一过程模型综合为控压钻井过程的全局模型,此模型通过耦合回压、泵流量、转速、钻压等主要操控变量来预测井底压力与机械钻速。
1.1 井筒环空压力预测简化模型
控压钻井过程如图1所示,其中,po、pp、pc、pbh分别为大气压、泵出口压力、井口回压和井底压力,Pa;qp、qbit、qc、qb和qres分别为泵出口流量、井底钻头流量、节流阀流量、回压泵出口流量和地层流体侵入量,m3/s。井下部分以钻头为分界点,分为钻柱与环空两部分。在一定假设条件下,将质量守恒与动量守恒构成的偏微分方程组简化并代入边界条件,得到有关深度、钻井液泵出口压力、回压、井底钻头流量的常微分方程组[7]:
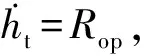
(1)

(2)

(3)
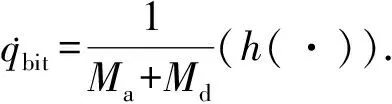
(4)

图1 控压钻井系统工艺图Fig.1 Process diagram of MPD system
井底压力计算方程为
pbh=pc+pa+ρaght.
(5)
辅助计算方程为
h(·)=pp-pc-pa-pd-(ρa-ρd)ght,
(6)
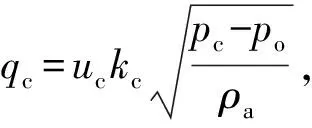
(7)
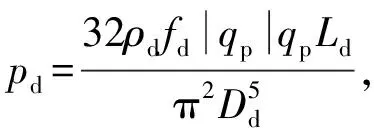
(8)

(9)
qres=Kpi(pres-pbh).
(10)
式中,pres为地层压力,Pa;βd、βa分别为钻柱和环空内钻井液的体积模量,Pa;Vd、Va分别为钻柱和环空体积,m3;Ma、Md分别为环空和钻柱中钻井液流动方向上单位截面密度的积分,kg/m4;pa、pd分别为环空和钻柱中钻井液流动方向的摩阻,Pa;ρd、ρa分别为钻柱和环空中钻井液密度,kg/m3;kc为节流阀的流量系数;uc为节流阀开度,%;ht为垂直井深,m;Da、Dd分别为井眼直径、钻柱直径,m;Kpi为与地层相关的系数,m3/(s·Pa);fd、fa分别为钻柱和环空的摩擦系数,s2/m6;Ad为钻柱的横截面积,m2;La、Ld分别为环空与钻柱长度,m;g为重力加速度,m/s2;Rop为机械钻速,m/h。
在实际控压钻井过程中,由于节流阀的流量系数难以确定,导致计算节流阀流量时准确性降低,通过式(3)可知,此时将无法保证回压的准确计算,进一步将严重影响井底压力的计算精度。因此本文中通过忽略式(3)和(7),即利用式(1)、(2)、(4)~(6)、(8)~(10)建立修正的环空压力预测模型。由于模型忽略了回压的微分项与节流阀的流量特性方程,故可以选用回压作为操控变量以替代节流阀开度,此选取方式更加接近实际情况。
1.2 钻柱系统非线性动力学模型
钻柱系统动力学模型包括集总参数质量模型与非线性摩擦扰动模型,其描述方程[8]为
(11)

(12)
钻头处受到的非线性扰动表示如下:
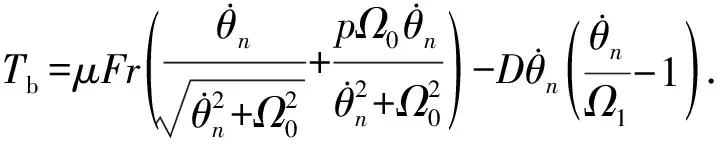
(13)

式(11)~(13)描述了钻柱旋转过程中的动力学特性,即在顶驱处施加一定的扭矩,会使各段钻柱转速逐渐增加并向井底钻具传递施加的驱动扭矩。由于钻柱系统受到非线性扰动的作用(式(13)),易出现黏滑振动现象[9]。钻柱黏滑振动会使钻进速度降低,钻柱和钻头使用寿命缩短[10]。
1.3 钻柱旋转与摩擦系数耦合模型
转速变化会引起钻进过程中摩擦系数的改变进而导致摩阻改变,两者关系较为复杂,常受流体性质(流变性和密度)、流态、直径比和偏心距的影响。当流体通过钻柱流经环空时,流体流态表现为层流运动,但由于钻柱旋转,流体流态可能转变为湍流,转变流态将会影响摩擦系数的大小,摩擦系数可以利用如下方程[11]确定:
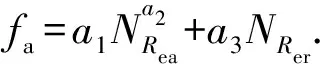
(14)
其中
式中,NRea为轴向上的雷诺数;NRer为旋转方向上的雷诺数;μea为轴向有效黏度,mPa·s;μer为径向有效黏度,mPa·s;va为环空流体的平均速度,m/s;a1~a3为待定系数。
1.4 机械钻速回归模型
机械钻速模型主要分为经验—机制模型与数据驱动模型。机制模型在早期得到了广泛的应用[12];近几年来随着机器学习方法的快速发展,数据驱动模型表现出更精确的预测能力[13],但同时具有更高的复杂度。在控制器设计的过程中,要求模型的复杂程度不能过高且易于工程实现,因此机械钻速模型选择Bourgoyne & Young(B-Y)模型[14],B-Y模型考虑了压实效应、岩石强度、压差、钻压、转速等诸多因素与机械钻速的关系,其描述方程为
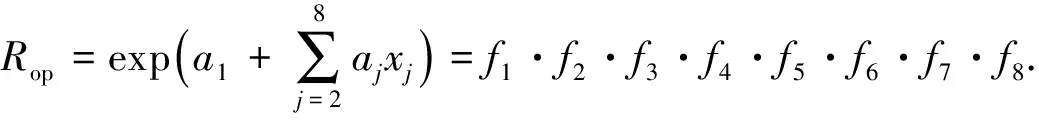
(15)
其中
f1=exp(a1),
f2=exp(a2(h0-ht)),
f4=exp(a4ht(gp-ρa)),
f7=exp(-a7h),
f8=exp(a8Fj).
式中,a1~a8为回归系数;f1为与地层强度有关的函数;f2、f3为与地层压实效应有关的函数;f4为与井底压差有关的函数;f5为与钻压有关的函数;f6为与转速有关的函数;f7为与牙齿磨损有关的函数;f8为与水力射流有关的函数;gp为地层孔隙压力当量密度,kg/m3;(w/db)t为牙轮钻头磨合期内所施加的钻压,kN/m;(w/db)为钻压,kN/m;h0为设定点深度,m;ρn为标准流体压力梯度,kg/m3;N0为转速阈值;h为齿高磨损量;Fj为射流冲击力,kN。
1.5 钻压传递动态模型
钻压是维持机械钻速稳定的主要因素。钻柱系统中除了驱动扭矩的传递外,在顶驱施加的压力将逐步传至井底。顶驱钻压的传递过程并不是快速的,且可能存在一定的滞后时间,描述方程应用一阶惯性加滞后环节[15]:

(16)
式中,WB为井底钻压,kN/m,其数值与式(15)中(w/db)相等;W为顶驱施加钻压,kN/m;b为过程增益;tp为地面钻压传至井底的时间,s;a为过程的时间常数。
1.6 多源变量间关联耦合
式(1)、(2)、(4)~(6)、(8)~(16)构成了控压钻井过程的全局模型,根据该模型分析井底压力、机械钻速、转速、钻压、回压等主要变量间的耦合特性。
式(1)为机械钻速的定义式,在钻进过程中,该式可以将机械钻速与井底压力紧密耦合在一起,式(5)表明,机械钻速可以直接影响井底压力,也可以通过影响式(2)、(4)和(9)间接影响井底压力。由式(11)、式(15)可以看出,顶驱转速通过影响钻头转速间接影响了机械钻速,而机械钻速发生变化又会直接或间接的影响井底压力。式(14)表明摩擦系数与环空流体平均速度、顶驱转速紧密关联,摩擦系数的变化会影响式(9)。式(15)中,地层孔隙压力当量密度可以表示为与井底压力、回压有关的函数表达式。式(16)可以看出,改变顶驱施加钻压可以影响井底钻压,井底钻压又将影响机械钻速。控压钻井过程全局模型的变量耦合关系如图2所示。
综上,由环空压力预测简化模型、钻柱系统动力学模型、钻柱旋转与摩擦系数耦合模型、钻压传递模型、机械钻速模型构成的控压钻井过程全局模型存在强耦合、严重时变、高度非线性等特性,而在以往控压钻井控制方法的研究工作中,仅考虑了单一系统模型,忽视了模型间的关联耦合。

图2 控压钻井过程全局模型的变量耦合示意图Fig.2 Variable coupling diagram of global model of managed pressure drilling process
2 模型求解
2.1 模型离散结果
将控压钻井过程全局模型表示为如下形式:
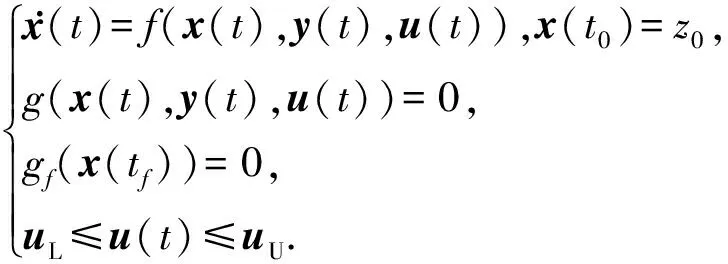
(17)
式中,微分变量x(t)∈X⊂Rn,代数变量y(t)∈Y⊂Rm,操控变量u(t)∈U⊂Rr,U为容许控制且是逐段连续函数的集合;x(t0)为模型初值;函数f:Rn×Rm×U→Rn的物理意义为由物料平衡、能量平衡构建的微分方程,对应全局模型中式(1)、(2)、(4)、(11)和(16);函数g:Rn×Rm×U→Rm的物理意义为由水力学构建的代数方程,对应全局模型中式(5)、(13)和(15);函数gf:Rn→Rπ为终端约束,该问题无终端约束项;t∈[t0,tf]为时间参数,t0和tf为定值;uL、uU分别为操控变量的约束低限与高限。
式(17)所建立的机制模型本质为微分-代数方程组(differential algebraic equation, DAE)表示的非线性系统,即一组微分变量与代数变量相互解耦的Hessenberg半显示DAE模型。引入index概念对代数方程的个数与维数进行刻画,已证明仅有index-1系统即模型中代数方程的个数与代数变量的维数相等且代数、微分变量相互解耦才可以直接离散化,而离散化高阶index系统需要模型重构[16]。
在全局模型中,式(5)、(13)和(15)三个方程分别对应了pbh、Tb、Rop三个代数变量,保证了式(17)为index-1型,故该模型可以使用直接离散化方法而无需模型重构。
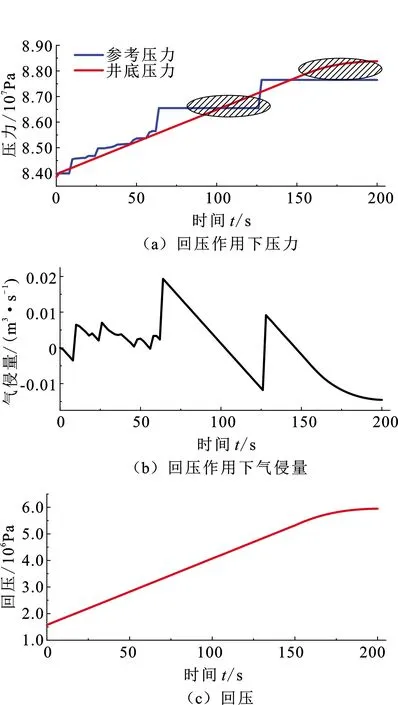
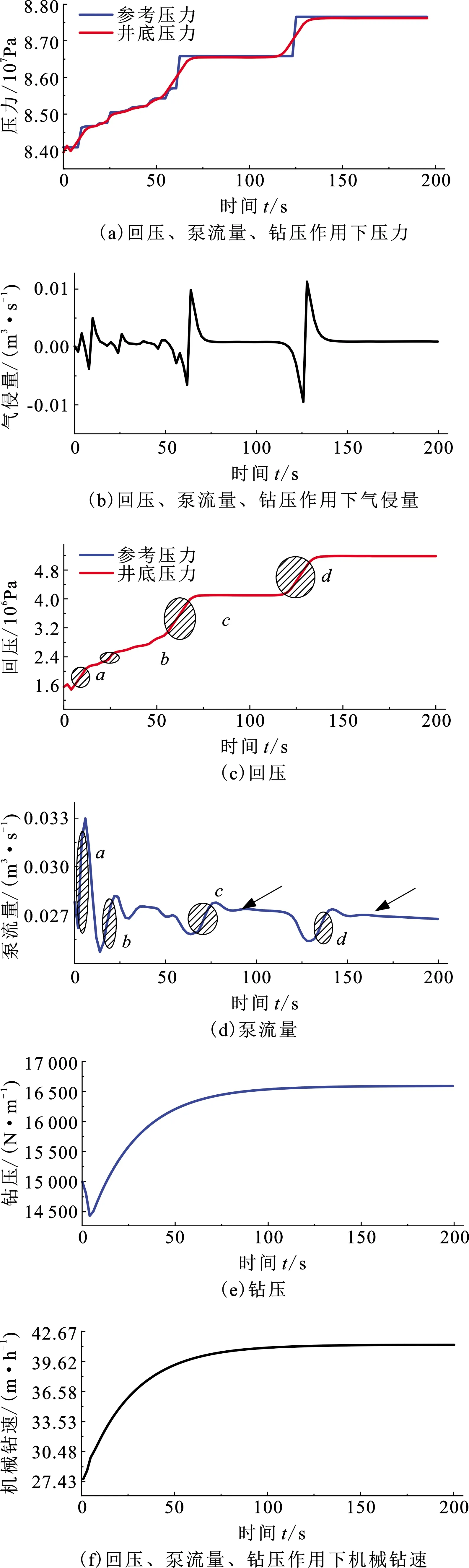
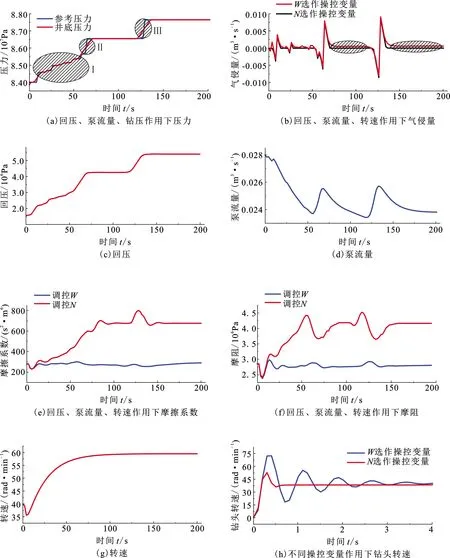
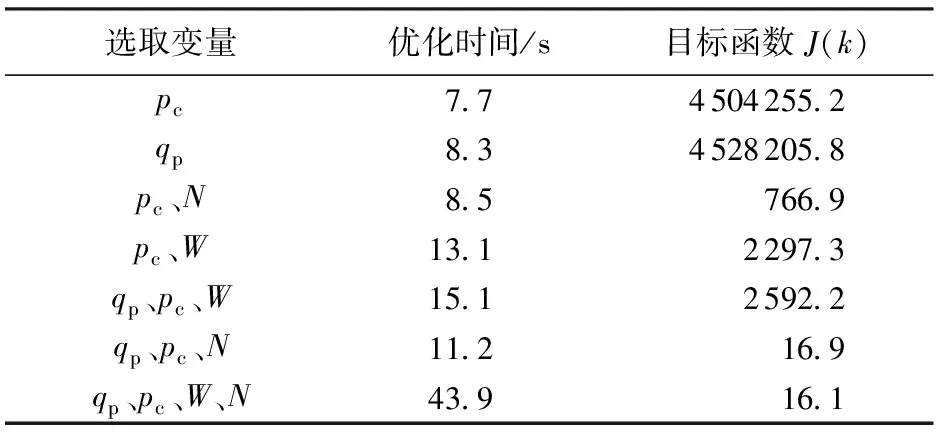
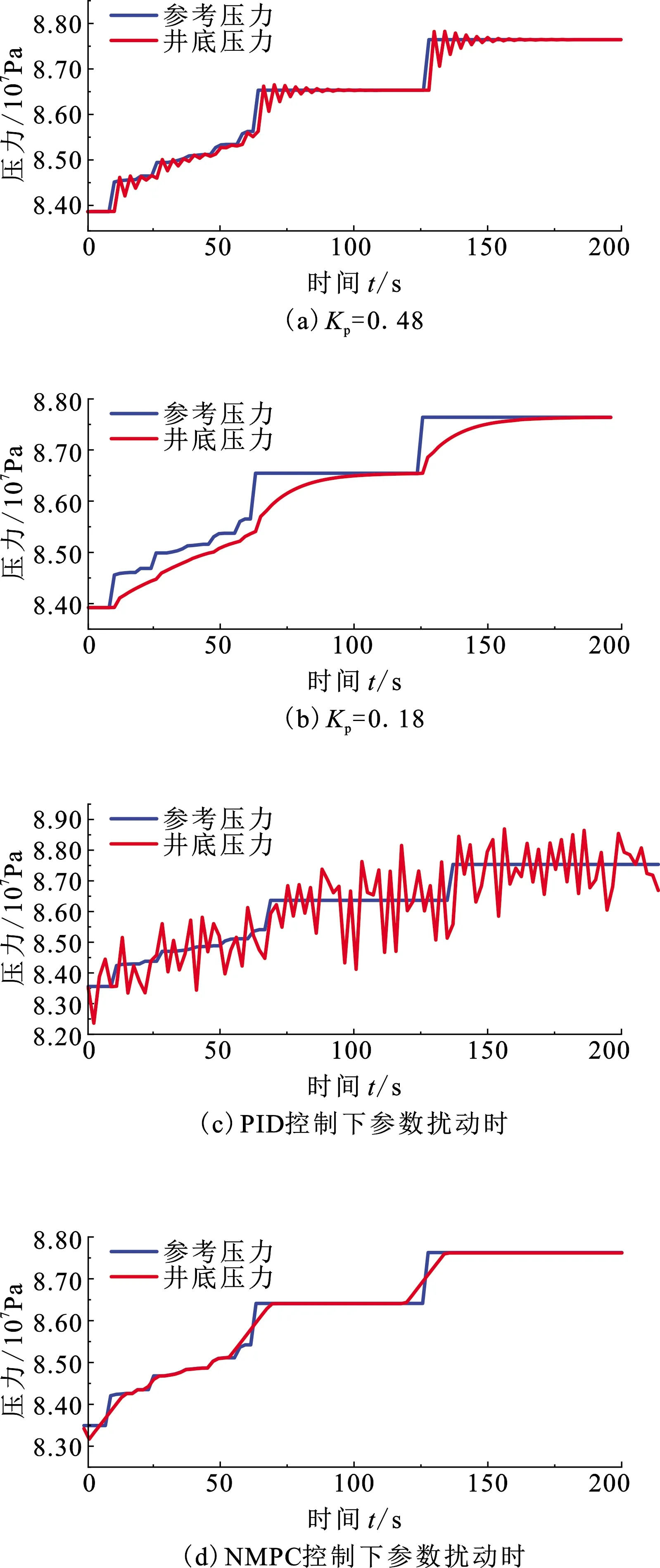
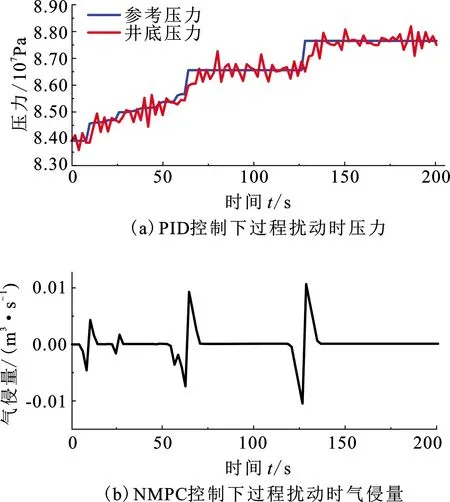
建立动态优化问题前,采用有限元正交配置法离散连续系统(17)中微分变量x(t)、代数变量y(t)与操控变量u(t),当正交多项式的根选作配置点时,能够以最少的配置点个数达到最高的代数精度,此配置方法称为正交配置。将区间[t0,tf]分为若干有限元(采样周期)t0 (18) t=ti-1+hiτ,t∈[ti-1,ti],τ∈[0,1],lj(τk)为Lagrange基函数,表示为 (19) 根据式(18)离散环空压力预测模型,表示为 (20) 其中g(·)、f(·)表示如下: f(·)=(pp)ji-(pc)ji-(pd)ji-(pa)ji- (ρa-ρd)g(ht)ji, (21) g(·)=(qp)ji-(qbit)ji-(Rop)ji·Ad. (22) 同理,钻柱动力学模型、机械钻速模型、钻压传递模型均采用相同的方法进行直接离散化。式(18)中x0,i+1=xK,i代表连接方程,它保证了有限元端点处微分变量连续,而代数变量与操控变量存在第一类间断点,如图3所示[16]。 图3 微分变量与操控变量离散化Fig.3 Discretization of differential variables and manipulated variable 采用序贯法对离散化模型进行求解,具体计算步骤如下: (1)输入初始条件,包括各参数及初始井深、泵压、钻头流量、顶驱转速、钻压、回压、泵流量。 (2)确定t0、tf,第i个有限元,该有限元内Gauss-Radua配置点情况。 (3)根据步骤(1)相容初始条件与离散模型(18),计算各配置点上微分变量、代数变量与操控变量值。 (4)判断微分变量与代数变量是否满足精度要求,当不满足精度时,判断是否达到终止时间tf,若达到终止时间计算完毕,若未达到终止时间迭代进入第i+1个有限元。 (5)在第i个有限元中,第K个配置点对应的计算值为第i+1个有限元起始配置点的初值,返回步骤(3)计算,若满足精度,计算完毕。 控压钻井优化控制系统中选定合适的控制策略是影响压力控制精度、钻井效率的关键因素。根据实际工程的需求,所选取的操控变量与被控变量均存在约束;并且在调控系统的过程中需要同时满足井底压力稳定与期望机械钻速。模型预测控制(model predictive control, MPC)的显著优势是可以在线处理给定的约束条件并综合不同性能指标。利用预测模型即本文中建立的控压过程全局模型预测系统未来的状态量和输出值,基于有限时域在线优化的方法,在每个采样时刻在线求解带有约束的二次规划或非线性规划问题。 由于实际对象中存在非线性特性,如式(4)、(13)~(15)等,若对其进行约简则会丢失系统特性,因此必须基于非线性模型设计相应的控制器才能保证更好的控制性能。综上,应用非线性模型预测控制(nonlinear model predictive control, NMPC)是可行且有必要的。 u(k+j|k),j=0,1,…,M-1. (23) 式(23)表示求解优化问题后,从k时刻到k+j时刻对系统模型施加的控制输入序列,一旦选定u(k),u(k+1),…,u(k+j)一组输入序列,NMPC并非将他们逐一全部实施,而只将序列的第一个元素u(k)=u*(k)即当前控制量施加到系统模型。因为预测时域保持一定长度,到下一采样时刻,该时域按一个采样周期向前滚动推移,故称为滚动优化[17]。 图4 滚动优化示意图Fig.4 Schematic diagram of rolling optimization 构建如下非线性规划(nonlinear programming, NLP)问题: (24) 定义第k时刻优化目标函数: (25) 控制器的工作流程如图5所示。首先,选取机械钻速与井底压差为被控变量,即z=[Rop,pbhd],两者均为代数变量。机械钻速是衡量钻进效率的关键指标,其参考轨迹wrR(k)需要由稳态优化得到。井底压力作为衡量井筒稳定性的关键指标,实际过程中必须将其控制在地层压力与破裂压力范围内,这意味着被控变量pbhd的期望值wrb(k)不再具有严格的参考轨迹,只要求控制在一定的区间内即可,因此为便于NMPC控制器设计,选择井底压差为被控变量,并使得wrb(k)∈[0,0.2](单位为MPa)。在控制过程中,期望pbhd总能满足区间约束条件,相较于定值控制,放松约束条件可以更加接近实际工程且保证钻进过程中压力的平稳控制。其次,给出微分变量x(t)及操控变量u(t)的约束限: (26) (27) 根据上述设计,以稳定井底压力、提升机械钻速、减弱黏滑振动幅值为综合性能指标,在考虑减少优化求解时间的前提下,选取式(27)中操控变量的不同组合方式,通过求解NLP问题,分析不同组合下变量间的协调控制机制,最终选定一组求解时间少、控制效果最佳的操控变量。 图5 NMPC控制流程Fig.5 Control flow of NMPC 利用序贯法对控压钻井过程全局模型进行开环仿真,并测试模型的跟踪能力;基于设计的非线性模型预测控制器分析多源操控变量间的协调控制机制,并选定操控变量的一组最优组合;从控制效果、抗扰动鲁棒性等方面与PID控制器进行对比,说明控压钻井过程非线性模型预测控制方法的有效性与先进性。表1为主要的钻井数据,其他物性参数见文献[15]与[19]。 表1 钻井数据 初始地层深度为6 000 m,参考压力(地层压力)为8.40×107Pa,地面转速为40 rad/min,地面钻压为15 000 N,回压为1.57×106Pa,泵流量为0.028 m3/s。图6(a)中,初始阶段参考压力连续小幅度增加,随后发生不同幅度的阶跃突变。通过参考压力发生不同幅度的变化可以测试模型的跟踪能力,试验结果表明,此模型具有一定的跟踪预测能力。图6(b)为气侵量的变化曲线,未施加控制算法时,参考压力的变化导致气侵量逐渐增加。由图6(c)可以看出,机械钻速上升并稳定至34.14 m/h。在深井钻探过程中,由于钻柱长度不断增加,导致模型(11)阶数不断增长且求解困难。文献[8]采用平衡截断法对钻柱进行模型降阶,因此图6(d)模拟了降阶后钻头处黏滑振动现象,钻头处转速呈现“上升—下降—上升”的变化规律。 图6 开环下各个变量的变化曲线Fig.6 Change curve of variables under open loop 以井底压差(pbhd)、机械钻速(Rop)为被控变量,对回压(pc)、泵流量(qp)、顶驱转速(N)、顶驱施加钻压(W)4个操控变量进行不同组合仿真试验:①仅选择pc为操控变量;②选取qp、pc、W为操控变量;③选取qp、pc、N为操控变量;④选取qp、pc、W、N为操控变量。满足综合性能指标且控制效果最好的即为最优组合。 4.2.1 仅选择pc为操控变量 由图7(a)、(c)可以看出,井底压力的变化完全取决于回压变化,仅调控回压无法保证井底压力的持续稳定。分析可知:当参考压力发生小幅度变化时,调控回压后未使得气侵加重;当参考压力发生较强的阶跃突变时,井底压力的控制过程出现了滞后现象(阴影部分),导致气侵量在50 s后发生较大波动,气侵未得到有效抑制。机械钻速的变化与图6(c)相似,仅控制回压并未提升机械钻速。当选取泵流量为单一操控变量时,气侵仍未得到明显抑制且无法提升机械钻速。尽管回压、泵流量紧密联系了水力学模型与机械钻速模型(图2),但选取单一操控变量并不能满足多性能指标。 图7 回压作用下各个变量的变化曲线Fig.7 Change curve of variables under back pressure 4.2.2 选取qp、pc、W为操控变量 由图8(a)、(b)可以看出,该试验可以较好地抑制气侵并跟踪地层压力。对比回压、泵流量的变化曲线:a处参考压力发生小幅度突变(0.5 MPa),回压与泵流量均出现上升,两者共同作用使得井底压力增加。a~b内参考压力缓慢上升,由于调控回压起主导作用,导致泵流量下降,此时两者变化相反,进而维持井底压力稳定。b处两者的变化与a相似,回压与泵流量同方向变化稳定井底压力。c、d两处参考压力发生了较强的阶跃突变,突变瞬间两者同时增加,但在参考压力稳定阶段(75~125 s、150~200 s),泵流量仅有小幅下降(箭头所示),这使得环空摩阻增加较小,最终未彻底抑制气侵。根据文献[11]可知,式(14)中a1、a3均为正值,a2为负 图8 回压、泵流量、钻压作用下各变量的变化曲线Fig.8 Change curve of variables underback pressure, pump flow rate and weight on bit 值,故当泵流量下降同时转速升高时摩擦系数才能进一步增大,并使得环空摩阻增加。 进一步分析可知,a、b、c、d处为快速跟踪参考压力的阶跃突变,回压与泵流量均呈现上升趋势,但相比于泵流量的变化,回压变化对井底压力的影响更大,泵流量上升可以减小环空摩阻,进而抵消部分回压快速变化对井底压力的影响。a~b内由于参考压力的缓慢变化,使得回压变化平稳,此时泵流量下降增大环空摩阻,共同跟踪参考压力。 由图8(e)、(f)可知,顶驱施加钻压在75 s达到稳定,同时,机械钻速基本稳定在41.45 m/h,与之前34.14 m/h相比提升了近21.41%。因此该选取方式初步满足了稳定井底压力与提升机械钻速的性能指标。 4.2.3 选取qp、pc、N为操控变量 由图9(b)可知,试验③最大的改进之处在于压力控制过程中完全抑制气侵,但调控过程与试验②略有不同。图9(e)、(f)为试验②与③摩擦系数及钻进过程中的摩阻变化。参考压力在Ⅰ处发生小幅度突变,泵流量持续下降,此时调控转速使得摩擦系数增大进而摩阻升高,同时配合回压增加以更好地稳定井底压力;Ⅱ、Ⅲ两阶段参考压力发生了较强的阶跃突变,突变瞬间回压与泵流量的变化与试验②相同,即均出现上升;在参考压力的稳定阶段(75~125 s、150~200 s),试验②摩阻值较小,而将操控变量切换至转速时,摩阻发生显著增加最终完全抑制气侵。此时稳定井底压力不仅取决于回压的变化,更取决于由钻柱旋转造成的摩阻变化,式(5)、(9)和(14)可以直观反映出流量与转速的变化通过影响摩擦系数进而影响井底压力。 由图9(h)可知,选择转速为操控变量时可降低钻头处黏滑振动幅值。试验②中选择钻压为操控变量,钻头处转速峰值为73 rad/min,而选择转速为操控变量时,钻头处转速峰值降至53 rad/min,减弱约27.39%。机械钻速的变化与图8(f)一致。 4.2.4 选取pc、qp、W、N为操控变量 对4个操控变量进行同时优化时气侵量与机械钻速的变化曲线与试验③相同。由表2可以看出,NMPC控制器选取不同操控变量时在线优化的时间不同,在选择4种操控变量时,尽管目标函数值达到最小,但优化时间大大增加;选取回压、泵流量、转速3种操控变量在保证较短计算时间的前提下使目标函数值较小,保证了良好的控制效果。 图9 回压、泵流量、转速作用下各变量的变化曲线Fig.9 Change curve of variables under back pressure, pump flow rate and rotation speed 表2 NMPC在线优化时间与目标函数值Table 2 Online optimization time and objective function value of NMPC 综上,选择回压、泵流量、转速为操控变量时在保证合理优化时间的前提下可以更好地稳定井底压力、提升机械钻速、减弱黏滑振动幅值,操控变量间的协调控制策略可以表述为:当地层压力发生小幅突变时(0.5 MPa),转速提升同时主泵流量降低,两者使得摩阻增加并协同回压增大精准控制井底压力;当地层压力发生大幅度突变时(1 MPa),回压与主泵流量同时增加以加快井底压力的变化;在地层压力保持稳定阶段,回压值保持不变,通过调节主泵流量与转速维持井底压力稳定。由于选取转速为操控变量,使得整个钻进过程中可以达到较高的机械钻速,同时协调其他变量保证井底压力稳定,并最大限度地减少停钻时间。 4.3.1 PID控制仿真 图10为选取合适的Kp、KI、KD参数后压力与气侵量的变化曲线。可以看出,气侵发生后,以回压为操控变量的PID控制算法可以达到抑制气侵的效果,但在初始阶段(阴影区域)控制效果不佳,控制过程中跟踪缓慢导致气侵量峰值较高,而以回压、泵流量、转速为操控变量的NMPC会补偿上述缺陷。 图10 PID控制下压力与气侵量的变化曲线Fig.10 Change curves of pressure and gas kick under PID control 4.3.2 两种控制算法鲁棒性分析 采用参数扰动与加入过程噪声两种方法测试不同控制算法的鲁棒性。 参数扰动分为控制器参数扰动与模型参数扰动。在PID算法中,当Kp发生|v|≥0.15的扰动时,控制性能发生剧烈变化(控制效果良好时Kp=0.33,如图10);当Kp=0.48时如图11(a),在参考压力发生不同幅度的阶跃变化时,井底压力会出现振荡现象且调节时间加长,使得抑制气侵效果变差;当Kp=0.18时如图11(b),井底压力的调节时间过长,调控滞后且气侵抑制缓慢。在NMPC算法中,选取误差权阵Q中井底压差pbhd对应的权重系数wbhd为调节参数。由图12可以看出,wbhd取值从10逐渐增加至2 500,控制效果逐步改善,这是因为参数变化过程中对误差的重视程度逐步增加,当权重系数大于1 500后,其受到幅值不大的扰动时控制效果无明显变化,这是PID控制算法中Kp、KI、KD不具备的抗扰动能力。 图11 控制器参数扰动与模型参数扰动下的 井底压力变化Fig.11 Bottom hole pressure variation under controller parameter disturbance and model parameter disturbance 模型参数扰动测试选取环空钻井液密度ρa为摄动参数,即该参数受到方差为σ1=20 kg/m3的高斯白噪声影响。由图11(c)可以看出,常规PID控制算法中选取Kp=0.33,当ρa受到扰动时,控制效果变差,无法稳定井底压力;图11(d)可以看出,NMPC在模型参数扰动时仍具备较好的控制效果。 在实际过程中,由于过程噪声的存在会使得模型失配,进而影响控制性能好坏。因此在式(5)、式(15)中分别加入过程噪声(σ2=0.2 MPa、σ3=1.5 m/h的高斯白噪声)。如图13(a)所示,在PID控制算法中,Kp同样取值为0.33,此时由于存在σ2=0.2 MPa的高斯噪声无法保证井底压力稳定;由图13(b)可以看出,当σ2、σ3同时存在时NMPC仍可以良好地抑制气侵,同时使得机械钻速达到41.45 m/h。 图12 不同权重系数下气侵量的变化Fig.12 Variation of gas kick under different weight coefficients 图13 存在过程噪声时PID与NMPC对井底 压力的控制效果Fig.13 Control effect of PID and NMPC on bottom hole pressure in the presence of process noise 综上,PID算法在选择合适的控制参数后可以有效抑制气侵,但当参数发生扰动或存在过程噪声时,控制效果变差,而非线性模型预测控制具备良好的鲁棒性,可以达到预期的控制效果。 (1)控压钻井过程全局模型可以同时反映出井底压力、机械钻速、钻头处黏滑振动等主要现象,该模型适用于控制器设计。 (2)常规PID控制器可以抑制气侵,但当模型及控制器参数发生扰动、过程噪声存在时,控制器无法保证稳定的控制效果。 (3)非线性模型预测控制器中操控变量的选取方式影响在线优化时间与控制效果,在不停止钻进且保证合理计算时间的前提下,回压、转速、泵流量三者为操控变量的NMPC控制器可以更加快速、稳定的抑制气侵,同时提高机械钻速、降低黏滑振动幅值,保证钻井安全与高效。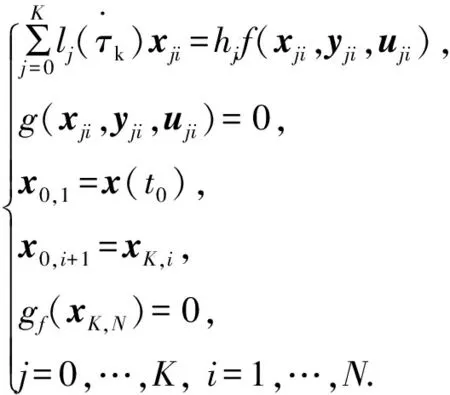
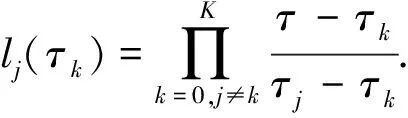


2.2 离散模型求解
3 多源变量协调控制方法
3.1 滚动优化
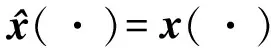

3.2 计算最优输入与反馈校正

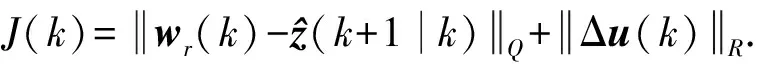
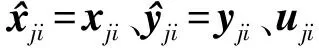
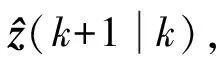
3.3 非线性模型预测控制器设计
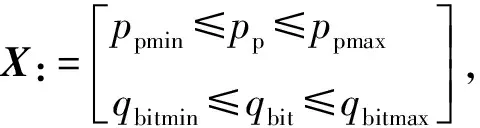


4 仿真实验验证

4.1 控压钻井过程全局模型仿真

4.2 基于控压钻井过程全局模型的NMPC仿真
4.3 NMPC与PID控制仿真结果对比


5 结 论

