快递末端共享配送网点模式及成本分摊

林百大，马翔宇

（1.山东科技大学 经济管理学院，山东 青岛 266590；2.山东科技大学济南校区，山东 济南 250031）

0 引言

自国家“十三五”规划以来，我国已成为全球发展最快、最具活力的新兴寄递市场。据国家邮政局统计数据显示，2020年全年快递业务量完成833.6亿件，同比增长31.2%。目前，快递服务的对象大多是网购消费者，货物种类复杂，规格差别大，消费者需求多样化，例如：服务到户、配送时效性高、取件时间自由等，这使得快递的末端配送相较于传统配送更加复杂。为此，各家快递企业都在积极探索创新最合理的配送模式，如：“蓝店”“菜鸟驿站”和快递企业与便利店合作的模式等。然而，在末端服务日渐复杂化的背后，也折射出建设自营网点成本高的问题。成本高主要体现在：初期的建设成本高，单家快递后期配送无法形成较大规模，浪费人力资源等。末端网点的运营困境与成本的持续上涨需要对配送方式进行创新，将独立配送网点转变为协作配送网点能够大幅度降低配送成本。

Guajardo，等指出在进行末端协作配送时，如何让企业组成协作联盟以及如何在联盟成员中分摊成本是两个最关键的问题。对于末端协作配送模式的创新，Zen，等提出让配送区域重叠度较大的末端配送企业组成一个配送联盟，由这个配送联盟为末端客户提供配送服务。王秀梅，等探索了一种共享配送网点和配送设施的共享型末端配送模式。Kexin Bi，等提出了一种基于智能终端服务站（IESS）的协同配送新模式。Savelsbergh，等在研究中提出实行末端协同配送是解决末端配送成本高的有效途径。Hsu研究了将独立的配送系统如何转变为协作配送网络。Xu，等认为由于中小型物流企业客户量少且分散，进而导致末端配送成本偏高，组建末端配送联盟是企业大幅度降低配送成本，实现企业进一步发展的有效途径。Liu，等和Van Heeswijk，等指出，针对目前末端配送效率不高的情况，通过组成末端配送联盟能够有效提高配送效率。徐丽，等在研究末端配送体系中指出，快递市场应该规范化，合理分配末端配送的投入方式。农村区域是典型的低密度区域，存在明显的配送成本高的问题，许茂增，等认为低密度配送区域能够通过配送联盟来降低配送成本。储涛，等研究发现通过搭建农村快递物流共享平台，能够有效解决末端配送体系建设成本高的难题。

末端配送联盟稳定的核心是成本（利益）分配，邓建新，等指出合理的利益分配是维持末端联盟稳定性的关键因素。Wang和Hong通过运用加入时间因素的Shapley值对共享配送中心和末端节点的利益分配进行了研究。Guajardo，等利用Shapley值时引入了时间因素。李柏洲，等将风险因子作为权重引入到Shapley值中进行修正，使得分摊的结果更加符合实际经济活动。

目前关于成本分摊的研究大多集中在末端协作配送路径中以及供应链内部企业的横向合作间，而对于快递企业共建末端配送网点和合作运营网点等方面的研究较少。从理论上分析，快递企业共建末端配送网点不仅有利于降低配送成本，还有利于提高末端配送资源的利用率，避免因重复建设网点造成的资源浪费。但是在现实中却又无法实现，这主要在于合作模式的成本分摊存在不公平的现象，导致许多企业对于共建配送网点的意愿不高。本文在我国末端配送的现实背景条件下，分析快递企业间合作共建末端配送网点的成本构成，并运用合作博弈方法解决共建网点的成本分摊问题。

1 问题描述与分析

目前，城市快递末端配送模式主要是由快递企业直接配送到户或者配送到各自的末端网点，在这种模式下，快递企业配送区域以及末端网点的交叉重合度高，容易造成配送资源的浪费。在目前的电商环境下，消费者多批次、小批量的消费需求以及对配送时效性的要求越来越高，促使物流配送企业组建末端配送联盟，共同建设末端配送网点。合作共建末端网点模式指的是多家快递企业出资共同建设某一区域的末端配送网点，由这一个网点完成这一个区域的配送，从而有效避免配送区域的交叉重合，整合配送资源，提高配送效率。

末端配送联盟的核心问题在于成本分摊，而“公平”恰恰又是成本分摊的核心要素，公平合理的成本分摊方案才能维持联盟的稳定。已知有n个快递企业组成配送联盟N，在某一三级节点配送区域内共同租赁建设M个末端网点，每个末端网点有K辆载重量为Q的同型号车辆，共有m个客户点需要配送。现假设N个快递企业在其三级节点配送区域内合作共同建设M个末端网点进行协作配送，求协作配送的车辆最佳路径，使配送成本最低（本文假设配送成本与配送距离成正比）。N个快递企业共同建设M个末端网点时，基于共享末端网点进行配送时所产生的成本有：第一阶段配送成本（即从三级节点运到末端网点的成本）1()，合作建设末端网点的固定成本2()以及第二阶段配送成本（即从末端网点配送到客户点的配送成本）3()。其中，第一阶段的成本属于快递企业单独运送到末端网点的成本，不存在企业之间的合作，因此只需要快递企业单独承担这一部分的成本，无需在各个快递企业之间分摊。如何将配送所产生的合作成本C()2()3()进行合理分摊是一个亟待解决的问题。故本文考虑n个快递企业组成配送联盟时，固定成本2()和第二阶段配送成本3()均用Shapley值法进行分摊。

对第二阶段配送成本3()进行Shapley值分摊时，存在2-1个子联盟S的配送成本3()，其中每一个3()的计算均涉及到一个VRP问题，即相当于求解2-1个VRP问题，从而得到子联盟S的配送成本3()。对建设末端网点的固定成本2()进行Shapley值分摊时，按照加入配送联盟的日流量（即日平均总单量）确定需要租赁的场地面积，从而确定固定成本2()。

2 基于共享末端网点配送模式的模型建立

2.1 模型建立

在计算协作配送成本时，需要一次性求解成本分摊所需要的2-1个成本输入数值，即可看作求解一个包含n个成员的VRG（Vehicle Routing Game）问题，等价于求解2-1个子联盟的VRP问题。

本文建模过程中所涉及的数学符号如下：

N：所有加入配送联盟的快递企业集合，{12}，n为加入配送联盟快递企业的数量；

M：建设末端网点的数量；

m：客户点的数量；

C：末端网点的待配送客户点的集合，{12}；

K：末端网点的车辆集合，{12}；

Q：配送车辆的最大载重；

q：第(1 ≤i≤) 个 客 户 点 的 需 求 量，且0≤q≤Q；

S：第(1 ≤j≤2-1)个快递企业子联盟，且≠∅；

c：任意两个客户点或者末端网点与一个客户点s,t之间的配送成本；

x：0-1变量，等于1表示配送车辆k∈K 经过弧()，其中s,t∈⋃O，否则等于0。

模型的基本假设条件为：

（1）每辆车的起点和终点均为末端网点；

（2）每辆车均不超过最大载重Q。

构建的模型如下：

目标函数：

约束条件：

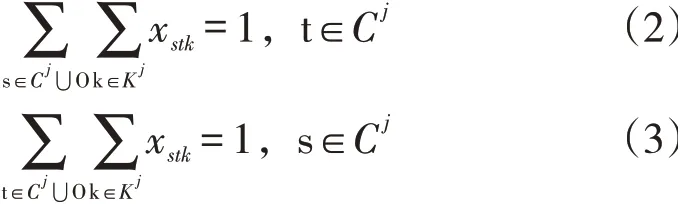
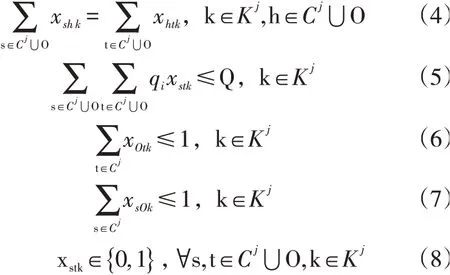
目标函数（1）是指最小化子联盟S中的企业第二阶段配送成本3()；约束条件式（2）和式（3）保证每个客户点被1辆车确切的服务一次；式（4）表示一辆车没有重复经过某个节点；式（5）表示每辆车在配送过程中不超过最大载重量；式（6）和式（7）表示配送车辆从末端网点出发，最后回到末端网点；式（8）是变量的取值范围。

2.2 输入子联盟Sj的方法

n个快递企业能够组成2-1个子联盟(1 ≤≤2-1)，其中第j个子联盟的配送成本为()，为了能够一次性输入2-1子联盟并且直观体现每个子联盟所包含的企业，采用长度为n的二进制0-1数组表示子联盟，引入子联盟序列变量j，将所有2-1个子联盟S根据其成员构成转换为二进制数组，再按照对应的十进制从小到大排序，最后求解对应的2-1个VRP问题。子联盟S的二进制数组如图1所示。

图1 子联盟Sj的二进制数组

3 算例分析

本节以山东省青岛市快递末端配送现状为例，通过设计算例展示n家快递公司拟在快递配送末端共同建设配送网点的求解步骤。

根据青岛市3家快递企业在其100km的三级节点配送区域内的某天配送量数据设计协作配送算例：假设边长为10km的正方形区域被等分为4个边长为5km的正方形区域，且每个正方形中各分布了一个配送中心，在边长为10km的区域内还随机均匀分布了企业1-企业3的顾客。其中a为高密度配送区域，b和c为中密度配送区域，d为低密度配送区域（即客户点少且比较分散）。

如图2所示，以图形的中心表示三个快递企业的三级配送中心以及末端客户的位置，其中大正方形表示快递企业1的三级配送中心，小正方形表示快递企业1的1-12个末端客户；大圆点表示快递企业2的三级配送中心，小圆点表示快递企业2的1-12个末端客户；大六边形表示快递企业3的三级配送中心，小六边形表示快递企业3的1～12个末端客户。

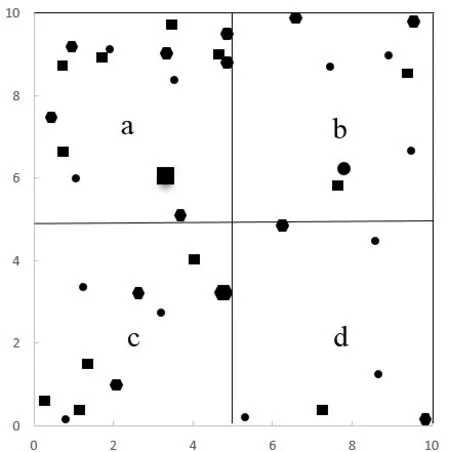
图2 末端网点及三级节点配送中心的位置

X和Y分别表示配送中心以及客户位置的横纵坐标，Q表示每个客户需求的快递量。配送中心每一辆车的最大载重为Q=100，且每个末端客户的快递量Q均为10，将两点之间的直线距离考虑为配送车辆的最短行驶距离，且每一辆车的单位配送成本为10，具体坐标值以及快递量见表1，其中序号01表示快递企业1的三级节点，序号1-12表示快递企业1的末端客户；序号02表示快递企业2的三级节点，序号13-24表示为快递企业2的末端客户；序号03表示快递企业3的三级节点，序号25-36表示快递企业3的末端客户。

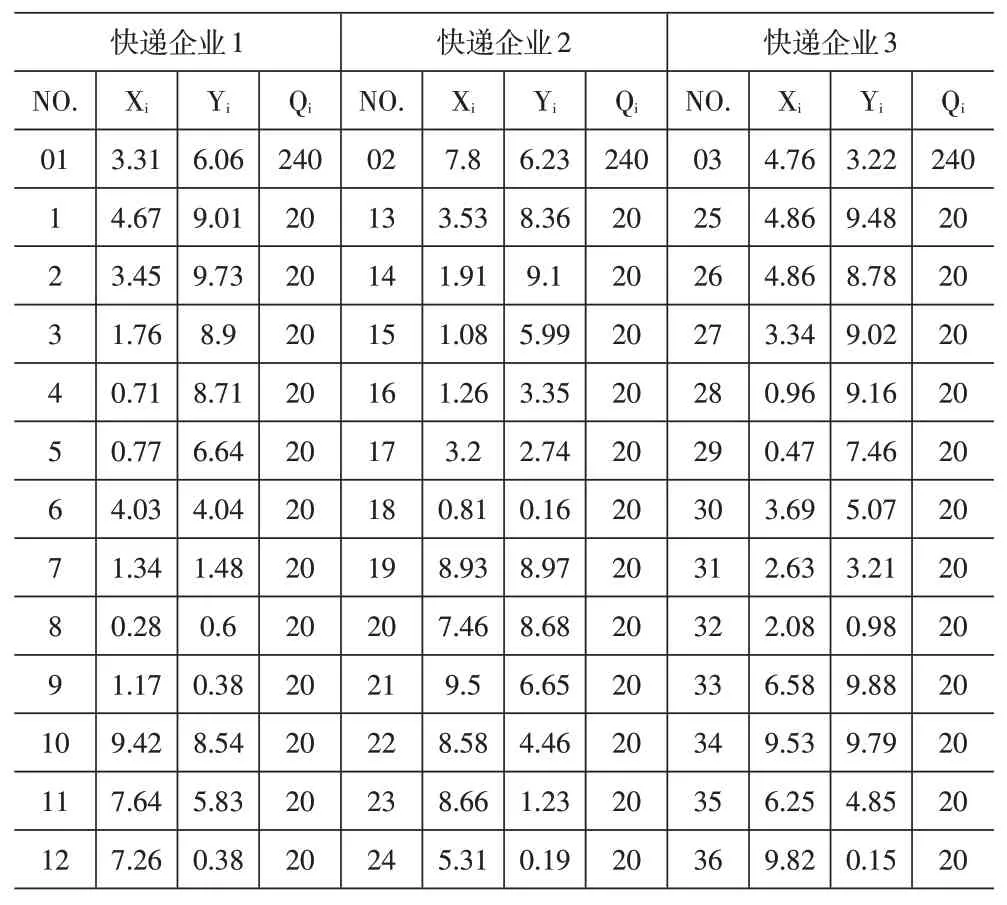
表1 末端客户和三级配送中心坐标位置及快递量信息

假设每个区域内共同建设末端网点的位置为：O（3.31,6.06），O（5.61,5.32），O（4.19,3.73），O（6.86,3.35）。

该配送问题包含三个快递配送企业，其中配送成本包含两部分：第一阶段由三级配送中心到末端网点的配送成本1()以及第二阶段从末端网点配送到客户的配送成本3()，第一阶段的配送只是由每家企业配送企业内部的货物，不存在调货等合作方式，因此这一部分的配送成本只需快递企业单独承担。第二阶段的配送属于快递企业协作之后的配送成本，需要对联盟内的成员进行成本分摊，因此需要求解2-1=7个非空子联盟的协作配送成本()，利用算法求解出7个子联盟中配送车辆的最优配送距离。求解结果见表2，其中NC-Dis表示协作配送之前的最优配送距离，C-Dis表示协作配送之后的最优配送距离。

表2 7个子联盟协作前与协作后的最优配送距离及成本

研究该配送问题时，在第一阶段的配送过程中，仅考虑一辆车服务一个末端网点，建设末端网点的固定成本根据青岛市租赁场地的平均市场价格核算，即年租赁价格为219元/m。因研究的配送问题是以日配送量为单位，需将固定成本折合为日均成本，即日均成本为0.6元/m/日，鉴于摆放快递所需要的面积较小，再结合算例中固定客户点的快递量，研究中按照租赁面积为5m进行计算。据此计算出7个子联盟协作前后的第一阶段配送成本以及建设末端网点的固定成本见表3，其中NC-1()表示协作前第一阶段配送成本，C-1()表示协作后第一阶段配送成本，NC-2()表示协作前的固定成本，C-2()表示协作后的固定成本，因为在协作前还是企业单独配送到顾客点，不存在建设末端网点，因此NC-1()和NC2()都为零。

表3 7个子联盟协作前与协作后的第一阶段配送成本与固定成本

通过计算得出协作前后的总成本以及节约的百分比见表4，协作前后的企业配送成本和节约的百分比，见表5，其中Save（%）表示总成本节约百分比，save（%）表示企业配送成本节约百分比。协作前的配送成本即企业单独配送到客户点的成本，协作后的成本采用Shapley值法进行分摊。

分析表4、表5可知：协作后配送联盟的总成本以及成员企业的配送成本都会较明显的降低，且联盟节约的百分比会随着联盟成员数量的增加而提高，即满足个体理性又满足整体理性。

表4 协作前后的总成本及节约的百分比

表5 协作前后企业成本及节约的百分比

4 结语

针对目前快递行业存在末端配送成本高、效率低下的问题，本文研究了快递企业共同建设末端配送网点，该网点介于三级配送节点以及客户点之间。通过合作博弈分析快递企业之间的协作行为，首先分析采用共享末端网点配送模式下的总成本构成，主要是由第一阶段由三级节点配送到末端网点的配送成本，共同建设末端网点的固定成本以及第二阶段由末端网点配送到客户点的配送成本三部分组成。据此构建一个总成本的数学模型，运用Shapley值法分摊总成本，得到联盟内每家快递企业需要分摊的成本值。同时，本文得出以下结论：采用共享末端网点的配送模式能够有效降低末端的配送成本，通过多组算例得出，随着联盟数量的增加，节约总成本的百分比将明显提高。

采取共享末端网点配送模式，客户既可选择到网点自取，也可选择配送员配送到门的服务。本文在研究中仅考虑客户选择配送到门的服务，未考虑客户到网点自取。自取模式下仅仅是客户行为，不存在配送员的配送路径问题，因此若加入客户到网点自取的情况，配送成本将会更低。在实践中，本文的理论成果可以用于指导快递企业共同建设末端配送联盟，并合理的分摊成本，不仅解决了不同快递企业配送路径重叠度高以及重复建设网点造成的资源浪费问题，而且提高了“最后一公里”的配送效率，降低了配送成本。