随机环境下考虑碳排放控制的拼车调度优化模型

李咏洁，袁鹏程

（上海理工大学 管理学院，上海 200093）

0 引言

网约车拼车出行已成为当前热门的出行方式之一，而传统拼车模型假设的拼车环境信息是固定已知且确定不变的，由于实际交通网络中交通事故、人为因素等影响使得拼车环境变幻莫测，导致传统拼车模型难以应用于实际交通环境中，同时影响着网约车行业的发展，车辆调度结果也无法令人满意。本文考虑到实际环境中驾驶员风险偏好对行驶时间的影响，对传统拼车模型进行优化，以此提高模型的适用能力。

行驶时间是决定拼车调度结果的重要要素之一，而实际交通网络中车辆行驶时间会因各种不确定性因素而变得随机。针对这一情况，李相勇，等建立随机行驶时间特征的车辆调度模型，通过两种优化方法求解模型，证明基于随机行驶时间的车辆调度模型具有求解的可行性。紧接着在研究影响时间因素时，Fu考虑到交通拥堵对行驶时间的影响，构建了随机行驶时间环境下的拼车模型，结果表明考虑时间随机特性的拼车系统具有更高的适用性；Schilde，等则考虑到行驶速度因素的影响，认为行驶时间因行驶速度的不同而难以确定，通过改进模型证明其可以有效提高车辆系统的稳定性。以上文献模型虽都考虑了随机行驶时间特性，但更多的是从客观因素上考究对时间带来的影响，而实际生活中主观因素同样也会对车辆行驶时间产生同样的作用。

因此，Heilporn，等开始从乘客行为角度考虑时间特性，乘客随机到达接送点从而导致行驶时间不再确定，研究发现乘客行为的异质性会对车辆调度产生一定的影响。Fu，等进一步考虑到乘客会根据自我偏好选择行驶路径，从而导致车辆的行驶时间因乘客决策而发生改变，研究表明尊重乘客意愿的拼车模型能很大程度提升拼车系统的服务能力。上述文献证明了考虑个体差异影响有助于提升网约车运营质量；但目前研究文献更多的是考虑乘客主观因素，忽略了驾驶员在拼车系统中的重要作用。在实际行驶过程中，驾驶员的风险偏好这一主观因素往往也会影响车辆的路径选择，更大程度上决定车辆行驶时间，这是因为在相同订单下不同风险偏好驾驶员路径抉择、驾驶行为是不一致的，因此，考虑驾驶员风险偏好影响行驶时间的拼车调度问题具有一定的研究价值。

与此同时，随着网约车行业的发展，大规模的网约车服务对交通环境产生一定程度的污染。这将不利于我国在2060年前实现“碳中和”目标，因此有必要针对运营车辆进行碳排放控制研究。在研究车辆与碳排放关系方面，邱玉琢，等探讨了碳排放规制下的生鲜农产品配送问题，通过规划配送车辆类型减少配送过程产生的总排放量。张如云，等从低碳角度对车辆配送路径进行优化研究，文献证明考虑车辆碳控制约束能有效降低实际配送过程中车辆产生的碳排放量。上述文献虽对车辆碳排放控制进行充分地研究，但目前该研究内容更多地集中在物流配送方面，对于网约车相关方面的研究数量并不多。为尽快实现“碳中和”目标，有必要对拼车系统中的运营车辆进行碳排放控制研究，通过控制车辆碳排放成本从而降低车辆的排放量，在运营商利益与环境保护之间寻求平衡。

为此，本文在传统拼车模型的基础上，对驾驶员风险偏好及车辆碳排放问题进行研究，以此构造随机环境下控制车辆碳排放的拼车调度优化模型。本文加入驾驶员风险偏好与行驶时间的关系模型，将车辆碳排放成本及行驶时间成本之和最小化作为目标函数，在满足约束条件下以成本最优为目标对车辆路径进行规划，该模型不仅更加适用于现实拼车环境，同时将运营商利益与节能减排的社会责任结合起来。

1 模型设计

经典拼车模型属于典型的NP难问题，因此本文模型也属于NP难问题。该模型在交通路网有向图()上进行研究，()为节点集合。集合N=P⋃D⋃{021}，其中{12}表示乘客上车点集合，{12}表示乘客下车点集合，为乘客订单请求数量。为顾客请求点，表示点对应的下车点，i∈N；点0和21分别表示车队出站和入站站点，位置相同。{12}为驾驶员集合，其中k表示驾驶员（k∈K）。

1.1 决策变量及相关变量

表1 决策变量描述

除决策变量外，本文模型中的其他相关变量详细信息见表2。

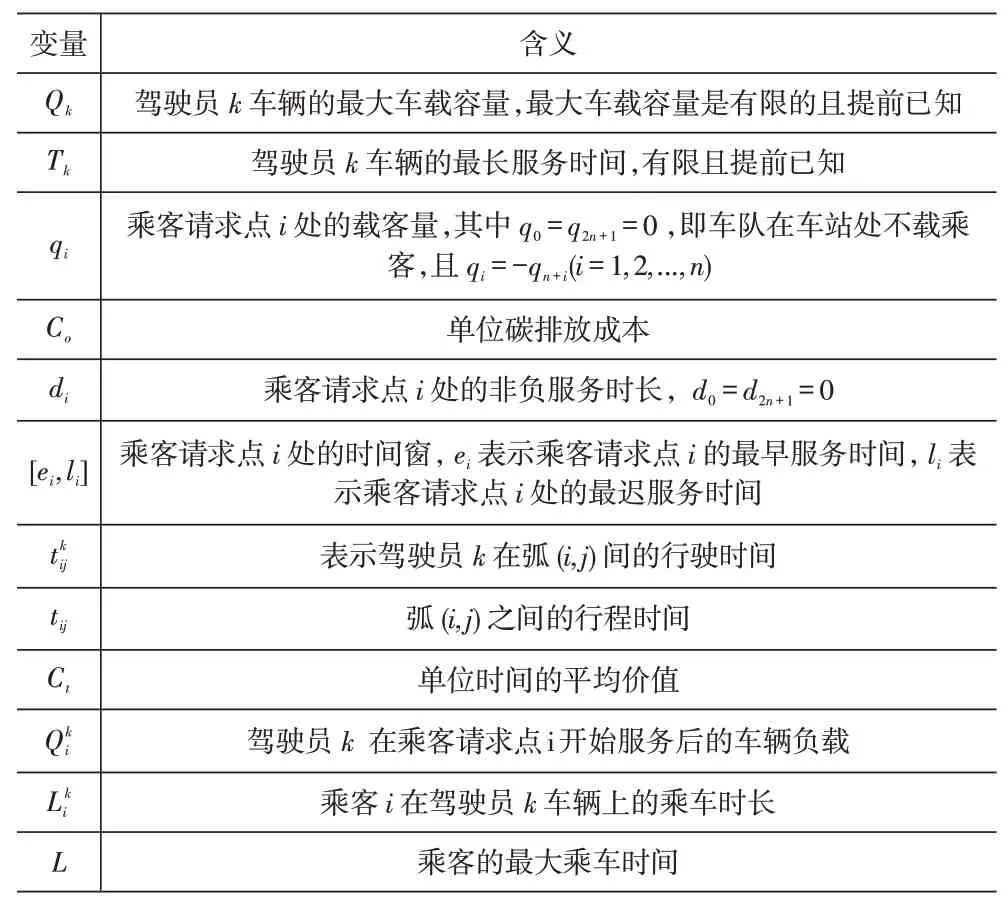
表2 相关变量描述

1.2 约束条件

本文主要从时间、车辆的载客量及路程三大方面对模型进行约束。

（1）容量约束。每辆车在行驶过程中的载客量不允许超过最大车载容量，从车站站点出发和返回车站站点时的车载容量均为零。

（2）时间约束。由车站站点和乘客请求点处的时间窗进行约束，即每辆车在乘客请求点的开始服务时间和结束时间应满足时间窗的约束，这些时间窗的约束是硬性且不允许违反的。其中点处开始服务时间不应在[e,l]之前启动，同时不应在[,l]之后启动；同时车队服从车站站点的时间窗要求；每辆车的服务时间不允许超过车辆最长服务时间，每位乘客的乘车时长均不超过最大乘车时间。

（3）路程约束。每辆车服务的起点和终点均是车站站点；乘客请求点和点由同一辆车进行服务，且i点先于点服务。

1.3 模型构建

在模型假设中，每个出行请求及出行顾客数量是提前已知的，订单执行过程中驾驶员与乘客的身份固定不变，所有乘客、车辆性质均相同，但每位驾驶员具有不同风险偏好。

1.3.1 风险偏好与行驶时间关系模型。本文将驾驶员风险态度分为风险趋向、风险中立及风险规避三种类型，不同风险态度影响驾驶员对路径的感知，每位驾驶员从自身效益最大出发，根据自身风险偏好特点决定车辆行驶路段。

本文假设行程时间服从正态分布，为避免行程时间存在负值的现象，本文参考文献[13]，假设行程时间呈截断正态分布，弧()之间的行程时间服从区间[]，参数为()的截断正态分布，记为~()≤t≤。

面对不同的风险环境，驾驶员采取不同的驾驶行为，弧间行驶时间与风险偏好间的关系模型如下：

式（1）中的为需要标定的常数量，取值范围为[01]，当0时，模型对时间假设条件与传统拼车模型一致，行程时间不具有随机特征且驾驶员不存在风险偏好的差异性。

1.3.2 行驶时间成本函数及碳排放成本函数。本文基于行驶时间随机特征，建立与时间相关的行驶时间成本函数，行驶时间成本是指驾驶员在行程上花费的时间所值的费用，由车辆行驶时间同单位时间的平均价值共同决定，设为单位时间的平均价值，见式（2）。

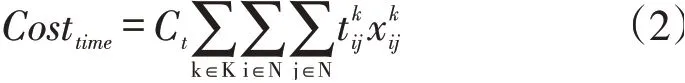
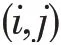
在行驶过程中，车辆行驶速度 i与油耗量遵循以下关系：

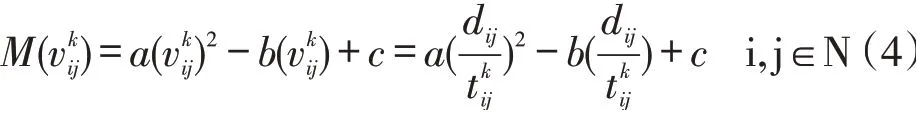
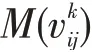
驾驶员关于速度与碳排放量的关系式为：

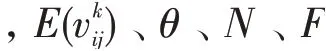
通过计算车辆碳排放量从而建立车辆碳排放成本函数，提出总碳排放成本函数式（6）。

式（6）中，为拼车系统所有车辆的总碳排放成本，为单位碳排放成本。

1.3.3 S-DARP模型构建。由于本模型将车辆行驶时

1.3 模型构建

间成本和碳排放成本之和最小为目标函数（见式（7）），对车辆容量、时间、路程建立模型的约束条件（见式（8）-（21）），在满足约束条件的前提下，以总成本最小对拼车车辆调度及路径进行优化，模型内容如下：

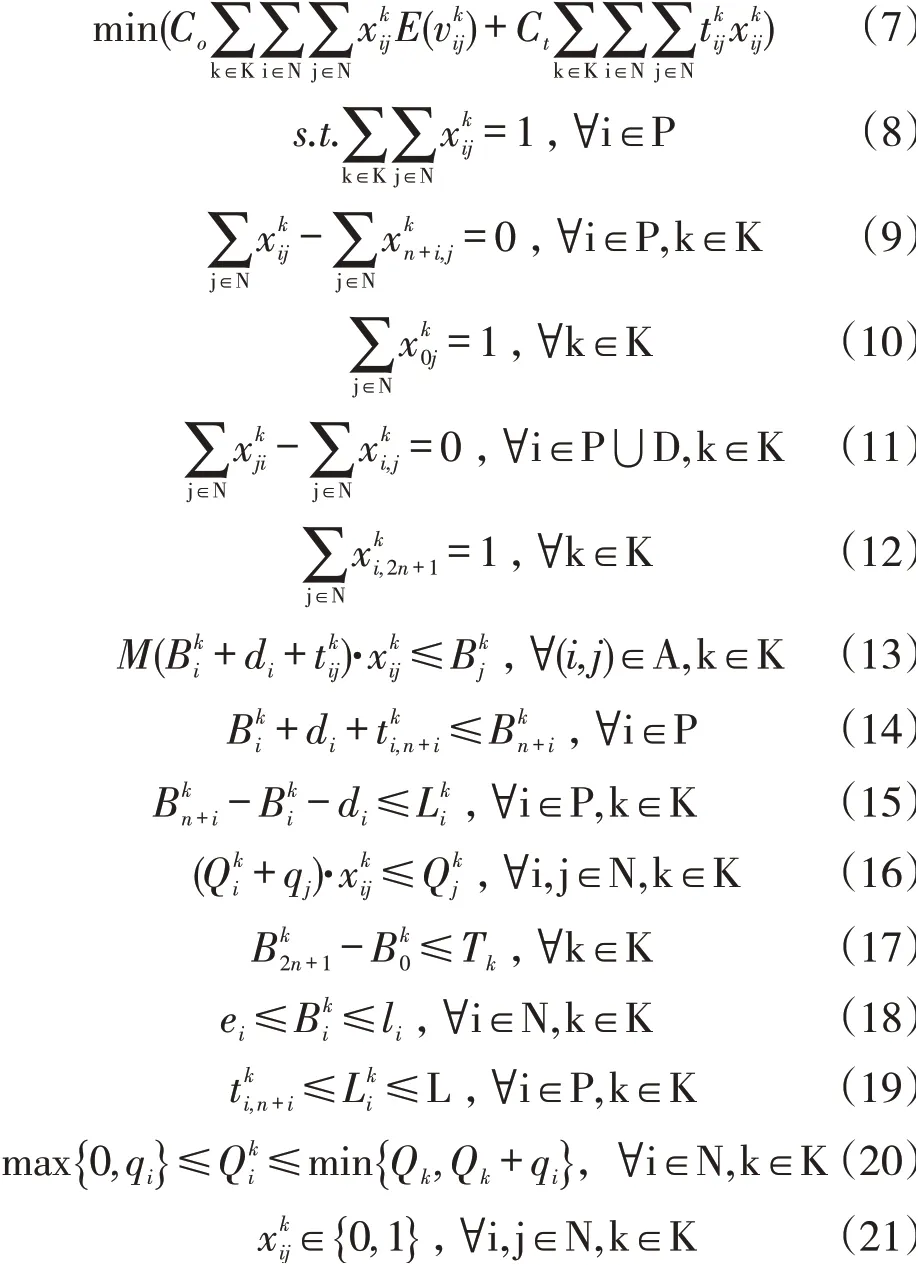
式（7）为S-DARP模型的目标函数，表示碳排放成本、车辆的行驶时间成本两项成本总和最小。式（8）和（9）表示乘客请求点i处必有车辆进行接送并且送达至对应的目的地点；式（10）和（12）保证了车辆必须从车站站点出发开始服务并且完成订单后返回至车站站点；每个乘客请求点处的车流量平衡由式（11）进行约束；式（13）和（14）保证车辆服务时间的连贯性，其中式（13）中的M为极大数值；而每位乘客的乘车时间由式（15）和（19）进行约束；式（16）和（20）保证了每辆车的车载容量的约束；在式（18）对每辆车在请求点i处开始服务时间进行时间窗约束的情况下，式（17）保证了每辆车的服务时长不超过其最长服务时间。

2 算例分析

2.1 数据预处理

本文使用能被LINGO求解的小规模算例。为保证算例的一般性，算例中所有乘客接送点均在二维矩形平面[1010]内随机生成，接送点坐标表示为[,y]，车站位于坐标轴中心（00），设计三组算例123，算例均由8名乘客和3名驾驶员组成。算例中共有16个接送点，分别为8个上车点和8个下车点，驾驶员车辆从车站起点（记为0）出发开始服务，返回车站终点（记为0*）结束服务。相关变量取值见表3，为时间窗长度，为乘客最长等待时间，为车辆最长服务时间，为乘客请求数，为驾驶员数量，参照文献[2]设置时间窗，所有实例的上下车请求呈均匀分布，上车请求点时间窗[,l]中的e在区间[0]内随机选取数值，对应下车请求点时间窗中[e,l]中的在区间[]内随机选取任意数值，和由时间窗的宽度进行定义，表4为三个算例中所有接送点的坐标位置及对应时间窗。行程时间呈截断正态分布，为简化计算，每段弧行驶时间的方差值从[08]区间范围内选取，行程时间的均值等于行程距离d，其上下限设为[][0)。

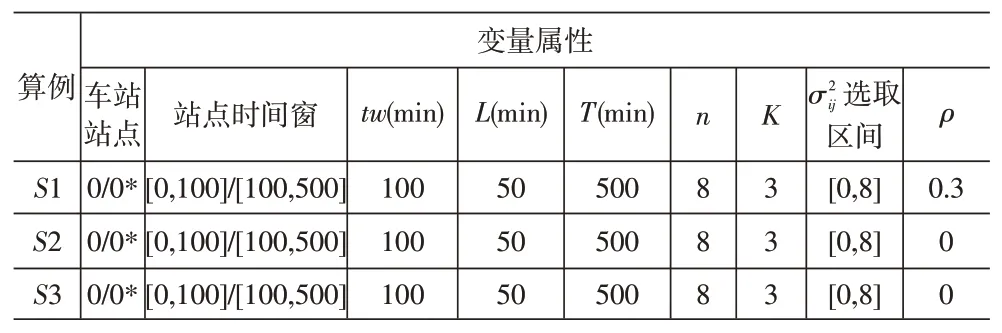
表3 相关变量取值

表4 乘客上下车坐标点及对应时间窗

燃油密度取95#汽油密度0.737kg/L，燃油缺省净发热值取汽油43MJ/kg、基于净发热值的二氧化碳排放因子F值为0.074 1kg/MJ、二氧化碳特征因子为1，碳排放价格取2015年1月5日上海碳排放交易价格26.6元/t，单位时间的平均价值等于驾驶员的时薪，设其值为30元/h。

2.2 算例结果

算例12以式（7）为目标函数，算例3则以传统拼车模型中的车辆总行驶里程最短为目标。所有算例约束条件均相同且规模大小一致。算例1考虑了行程时间的随机性并设计了3名不同风险偏好的驾驶员，风险厌恶型驾驶员记为1，风险趋向型驾驶员记为2，风险中立型驾驶员记为3；23不考虑行驶时间的随机性和驾驶员的风险偏好，假设3名驾驶员1、2、3均为同质。即算例1求解结果为本文模型求解结果，算例2结果为不考虑驾驶员风险偏好仅考虑碳排放成本的求解结果，算例3结果为传统拼车模型求解结果。

表5给出了LINGO求解后每个算例中每位驾驶员的行驶路径、总里程及对应的总成本数值。算例1共3辆车运送8名乘客，风险厌恶型驾驶员1服务1名乘客，风险趋向型驾驶员2服务5名乘客，风险中立型驾驶员3服务2名乘客。2和3算例路径结果相差不大，结果均为1服务2名乘客，2服务3名乘客，3服务3名乘客。

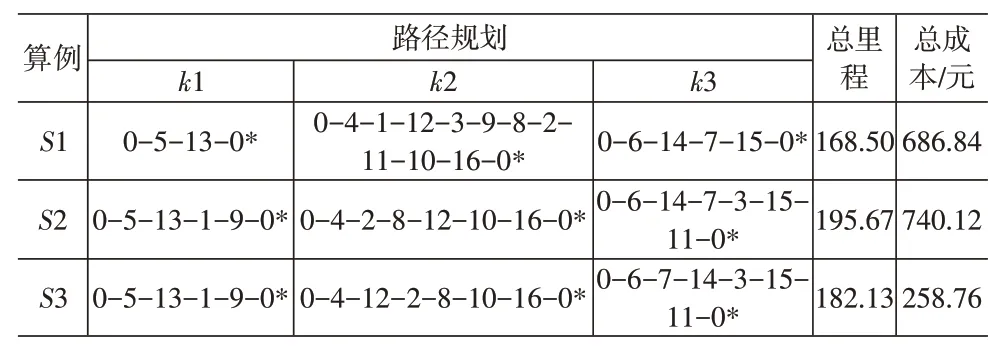
表5 算例结果

2.3 结果分析

从表5可以看出，从路径规划上看，在随机环境下风险趋向型驾驶员服务乘客数量最多，其次为风险中立型驾驶员，风险厌恶型驾驶员服务数量最少。原因可能是风险趋向型驾驶员愿意承担一定的风险从而实现其个人总行驶时间最短，在总成本最小的目标下，分配给风险趋向型驾驶员的订单数也最多。算例2不考虑随机行程时间特征，但考虑了碳排放成本，其行驶里程比1增加了27.17km，总成本增加了7.76%，考虑驾驶员风险偏好会对车辆总行驶里程产生较大程度的影响，而总成本也相应有所增加，因此随机环境下考虑驾驶员风险偏好特性不仅不会增加车辆的行驶里程，同时还减少了总成本的支出。

算例3为传统拼车模型求解结果，其总成本结果均小于1和2，但其行驶里程比1增加了13.63km，比2减少了13.54km。同样在不考虑随机因素的静态环境下，3的总行驶里程要比2少，因此车辆碳排放可能不单单与车辆行驶里程有关，还与其他因素有关。

3 结语

将驾驶员风险偏好的差异特征纳入车辆行驶时间影响因素中进行考量，并且在考虑随机行驶时间情况下加入车辆碳排放控制策略，构建在随机环境下考虑碳排放控制的车辆调度优化模型。该模型提高了拼车模型在现实环境中的适应性、减少车辆运行过程中的污染。从是否考虑随机环境的优化结果比较可以看出：随机环境下的拼车模型会根据驾驶员风险偏好类型进行规划路径，但不会增加车辆总行驶里程和总成本，因此考虑驾驶员的风险偏好不仅会考虑驾驶员个体差异还有利于减少运营商成本开支。从考虑碳排放成本安排下的优化结果可以看出：车辆碳排放量不仅与车辆总行驶里程有关，还与其他因素有关。综合来看，本文构建模型求解算例的总行驶里程最优，考虑随机环境特征并加入碳排放成本控制不仅不会增加车辆行驶里程，还有助于降低总成本支出，有效减少车辆碳排放污染。

在实际交通网络中，路径行驶时间除了受驾驶员风险偏好特性影响外，还受多种因素的影响，考虑多因素影响下的拼车问题将是作者今后的研究方向。