数学定理在初中物理解题中的应用

摘要：对于进入初中的学生来说，物理是一门新的学科，物理解题能力是学生必须具备的能力.同时，物理和数学有着密切的关系，在物理解题中需要应用一定的数学知识和定理，利用数学定理解决物理问题是初中物理学习中考察的重要内容.随着课程改革的深入，对学生多学科综合学习能力提出更高的要求，综合性学习成为教育发展的必然趋势，对初中物理教师提出新的要求.本文就初中物理解题中数学定理的应用谈谈认识.

关键词：初中物理解题;数学定理;应用策略

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）11-0107-03

收稿日期：2022-01-15

作者简介：吴建春（1976.12-），男，福建省龙岩人，本科，中学一级教师，从事初中物理教学研究.

在初中阶段的教育中，不仅仅考查学生对知识的掌握，同时考查学生对知识的应用能力，利用数学定理解决物理问题能力是重要的考查内容.在初中物理教学中，无论是物理定理表达，或者是物理问题解答，都需要借助数学这一工具.在初中物理解题中，数学定理应用较为广泛，借助数学定理解决物理问题，提高学生解题能力.

1 初中物理解题中应用的数学定理知识

1.1 借助相似三角形定理解题

初中物理解题中，不少题目需要相应的特定条件，保证其取值范围的科学性.在实际的解题过程中，需要对题目进行分析，利用相应的几何知识或定理，相似三角形定理是应用较多知识，借助其知识内容对物理知识作为形象分析，画出相应的图形，掌握其中的逻辑关系，为科学计算做好准备，保证学生能够快速解题.

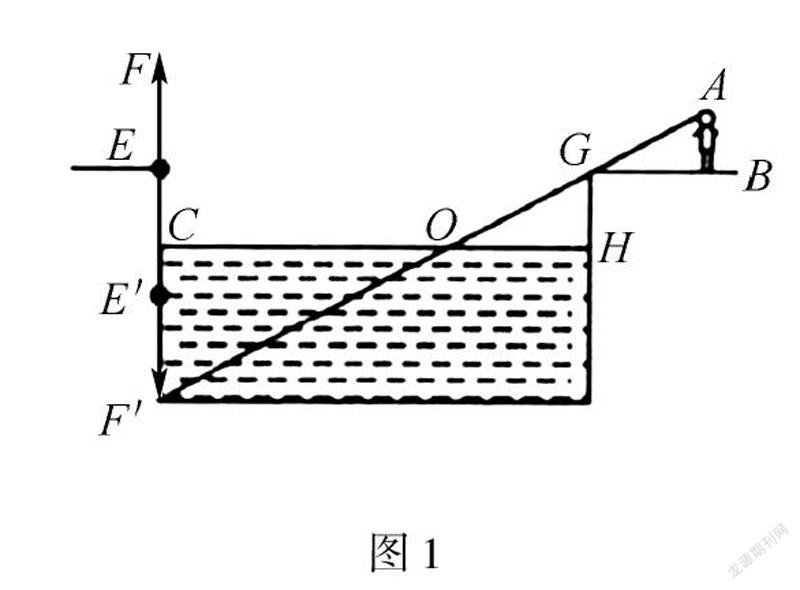
例题：在图1中，某人在河边看到对岸的树EF，此树在水中的成像为E′F′，如果此人向后退6m，则不能够看到此树在水中的全部成像.已知人的身高是1.8m，河岸比水面高1m，河的宽度是40m，求树的高度.

在此题解答时，将水平面作为镜面看待，树在水中的成像和水平面堆成，因此，可以利用相似三角形原理进行思考和解答.在解题时，通过观察和分析，可以得知三角形COF′与三角形HOG、三角形BGA属于相似三角形.通过计算得出CF′为11m，河岸比水面高出1m，所以可以得出树高为10m.

解根据平面成像原理分析，结合图形可以得出CO∶CF′=OH∶GH=GB∶AB.根据题目已知GB=6m，AB=1.8m，GH=1m，解答得OH=10/3m，因为CO∶CF′=10/3，所以得出CF′=11m，进而得出EF=10m.

在初中物理解題中，部分题目需要利用相应的数学知识和思维，借助相似三角形相关概念和原理，对题目做出更加细致形象的分析，有效解答物理问题.

1.2 利用函数定理解题

初中物理解题中，通过图像对物理过程做出描述，更为直观的体现出数学思想.函数知识是初中学生学习的重要知识，借助函数的相关定理解决物理问题，更加有利于学生理解题意，明确解题思路.初中物理教学中，函数知识的应用对学生来说较为简单，能够帮助学生更好的解题，拓展学生解题思维，培养学生物理解题信心，提升学生物理思维.

例如，在“匀速直线运动”的解题中，在路程和时间图象理解中有着一定的难度，不利于学生的思考和解题.面对此类型的物理题目，引导学生绘制相应的一次函数图像，结合一次函数相关定理，分析和解答问题.借助这样的方式，将物理问题转化成数学问题，通过数学知识和原理展现出来，锻炼学生物理解题能力.面对密度相关的题目同样可以利用函数知识原理解题，

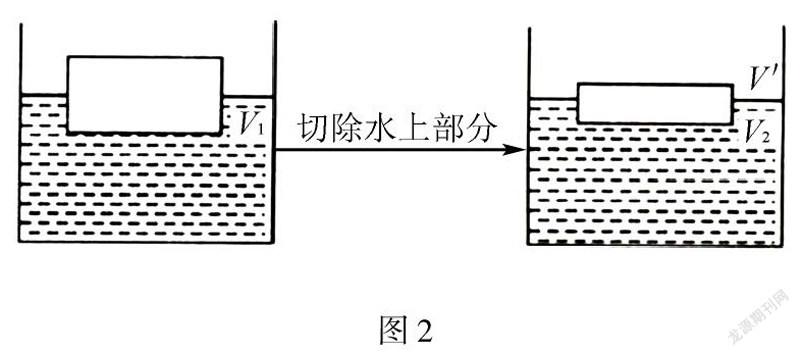
例题：如图2中所示，实心长方体的体积为V，将其放入到水中，其静止漂浮在水面，水下部分体积为V，将露出水面的部分切除，余下部分放入水中，当余下体积处于静止状态时，露出水面体积V′和总体积V的比值最大，求解长方体的密度.

在解题时，假设水的密度是ρ，长方体的密度是ρ2，根据物体在液面漂浮，可以得出V/V=ρρ，得出V1=ρ/ρV，通过观察分析可以发现，体积的比值是长方体密度和水密度决定的，与其体积没有关系.即便是将剩余部分放入水中静止，其水下部分体积和总体积的比依然是密度比.在解题时，假设余下部分露出的体积为V′，切除后水下部分的体积为V，整体为V，可以得出V=ρ/ρV，将公式带入得出V′和V的比值为V′/V=-（ρ/ρ）+ρ/ρ+0，可以将其作为二次函数，求解其最大值，完成密度求解.

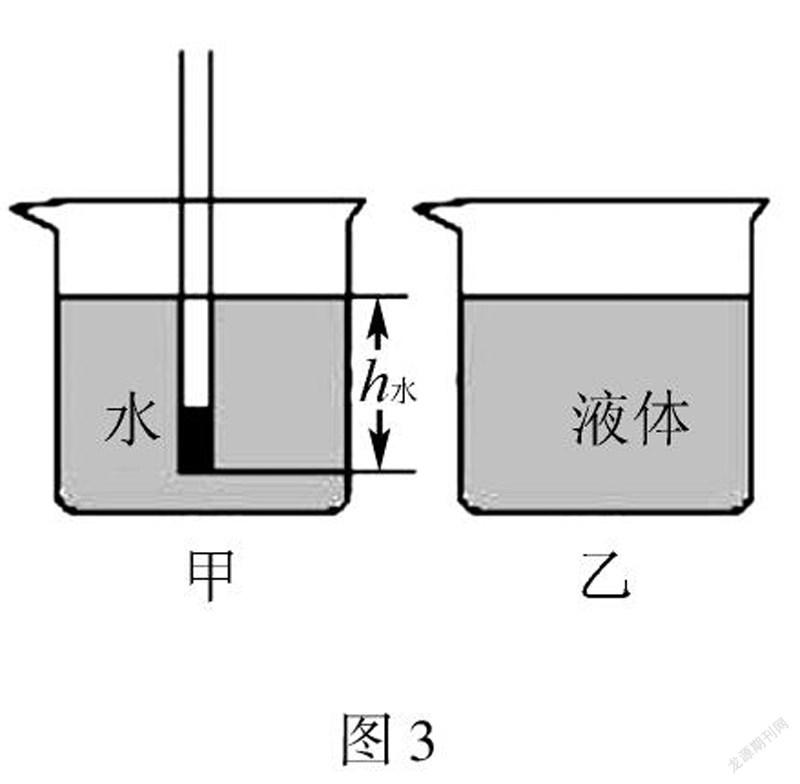
例题：饮料吸管下端加适当的配重并用石蜡封口制成一个简易密度计，并用一杯水和刻度尺来测量液体密度，如图3甲所示.（1）这种简易密度计的刻度线分布是_________的.（选填“不均匀”或“均匀”）（2）现有两根仅粗细不同的饮料吸管制作密度计，为了使测量结果更精确，应选择__________的吸管.（选填“粗”或“细”）

有关自制器材的刻度均匀问题及精度改变问题是近年中考的高频考点，但这类问题往往让学生无从下手，如果能列出相关的函数关系式，问题就迎刃而解.将吸管竖直放入水中，静止时测得吸管浸入水中的深度为h;将此密度计置于被测液体中静止时测得吸管浸入水中的深度为h，由于吸管在水、液体中都是漂浮的，所以F=G;因为吸管为柱状设吸管的底面积为S，则据阿基米德原理可得： ρgSh=ρgSh，所以h=ρ/ρρ.因为ρ、h都不变，所以h与ρ构成反比例函数，所以其刻度线的分布是不均匀的.设粗细不同而G相同的吸管制作的密度计漂浮在同种液体中，因为F=ρgv=G，所以v相同，据h=V/S可知h与s成反比，所以越细的吸管，h越大，测量结果更精确.

目前，在初中物理教学中的相关函数定理知识应用包括：正比例函数、反比例函数、一次函数、二次函数的简单应用，但学生应区别楚清应用不同函数的题目的特征，避免混淆.

1.3 利用方程知识定理解题

物理和数学学科有着非常密切的关系，两者是相互促进和发展.在初中物理解题中，方程定理知识是常用的内容，很多的物理定理和规律可以通过函数表达，要求学生掌握相应的方程知识，明确物理解题思路，提高学生解题效率和质量.

例题：两个定值电阻分别是R、R，通过某种形式连接接入电路，R消耗的电功率是12W，将两个电阻通过另外一种方式接入连接，接入电路之后，其总电流是9A，R消耗的电功率是108W，求解两个电阻的电阻值.

在解题时，通过题目中的已知条件可以得出电源电压不变是前提条件，可以假设为U.根据物理相关公式，P=U/R，当电阻不变时，其两端的电压越小，消耗功率越小.因为第一次R消耗的电功率比第二次的小，所以第一次R两端电压小于第二次R两端电压，从而得出第一次R、R是串联电路，第二次R、R是并联电路.根据串联电路特点，列出（U/R+R）·R=12W;根据并联电路特点，列出U/R+U/R=9A;再与U/R=108W组成方程组，完成问题的解答.

1.4 利用比例知识定理解题

初中物理问题解题时，会遇到利用数学比例、比值解题的情况，主要有两种类型.第一类是公式中只有两个变量.此类问题较简单，因为只存在正比（或反比）两种情况.

例如：（成反比情况）甲、乙两船的平均速度之比为v∶v=2∶3，当它们航行相同的路程时，所用时间之比为_______.本题公式是v=s/t，依题意路程s相同，则时间t与速度v就成反比，因此可得： t∶t= v∶v=3∶2.第二类是公式中有三个或三个以上的变量时，可按相关公式写出比例式再代入数据化简求值.

例题：两种液体吸收热量比为1∶2，质量比为2∶3，它们升高温度比为3∶4，则这两种液体的比热容之比是________.本題所用公式Q=cmΔt，其比例式为Q/Q=c/c·m/m·Δt/Δt，代入数据得1/2=c/c·2/3·3/4，化简可得c/c=1/1.

在学生解题时，学生利用比例和比值的相关知识定理，能够很快将问题解决，提高学生物理解题效率.

2 加强物理实验教学与数学定理应用的结合

物理是一门注重实践的学科，实验是物理学科的重要内容，借助数学定理与实验数据相结合帮助学生发现物理规律，并能熟练应用数学定理去解决问题.在学生利用数学定理解决问题的同时，培养学生解决实际问题的思维和能力，提高其高阶的思维能力.作为物理教师，需要让学生认识到物理和数学知识之间的重要关系，也要了解其存在局限性，数学定理是物理问题解决的工具，实验是物理注重的内容，同样重视解题方法和思路，带领学生开展相应的物理实验，培养学生动手能力，借助相应的实践活动，让学生体会物理学科的真谛，掌握多种解决问题的能力、方法和技巧，提高学生的物理核心素养.

初中物理解题中，利用数学定理知识分析和解题，能够强化学生逻辑思维，形成学生良好的物理意识，借助数学方法对物理抽象题目进行简化，引导学生的思维能力向纵深发展，逐渐形成良好的解题能力.实现学生数学思维和物理思维的融合，保证数学定理在物理解题有效利用，提高学生的物理素养.因此，在具体解题中，借助数学定理，可加深物理知识理解和掌握，提高学生学习效果，更好的学习和掌握物理知识.

参考文献：

[1] 黄宝华，林超.例谈初中物理解题中数学知识的应用[J].名师在线，2019，78（05）：13-14.

[2] 李建录.浅谈数学方法在初中物理解题中的应用[J].中学物理，2016，34（16）：75-76.

[3] 肖会清.浅谈数学知识在初中物理解题中运用[J].中学课程辅导：教师通讯，2020（01）：69.

[责任编辑：李璟]