速度滑冰如何减小空气阻力1)

陈晓东 何国胜 杨秀峰 胡 婧 王 宁

*(北京理工大学宇航学院,北京 100081)

†(中央广播电视总台,北京 100020)

速度滑冰简称速滑,是滑冰运动中历史最为悠久,开展最为广泛的项目[1]。速滑运动员踩在1 mm 厚的刀片上在冰面上飞驰,平均速度可以达到14 m/s 左右,也就是约50 km/h。速滑运动员如何在比赛中滑得更快呢[2]？除了需要通过平时的刻苦训练,提高身体素质之外,还需要考虑如何在比赛中减小所受到的阻力[3-4]。

运动员受到的阻力,即与滑行方向相反的力,包括来自冰刀与冰面之间的摩擦力和空气阻力。研究表明,速滑运动员达到恒定速度时,冰面摩擦力占总阻力的20%左右,而空气阻力则占总阻力的80%左右[5]。因而,减小空气阻力是提高比赛成绩的关键。

在2014 索契冬奥会男子团体追逐决赛上,韩国队和荷兰队争夺金牌,赛况相当激烈,韩国队出发不错,中途也紧紧咬住荷兰队,不过从后半程开始,荷兰队长距离的优势显露出来,最终荷兰队夺得金牌。我们在观看比赛的时候可以发现一些特点,比如运动员都穿着紧身衣,滑行时身体尽量平行地面,手臂尽量放到身后,后方运动员尽量跟紧前方运动员,比赛过程中,各队选手一直在不断变换位置,由不同的队员来领队滑行。这些策略都与空气阻力有关。下面介绍一下空气动力学是如何应用于速度滑冰项目,帮助运动员提高比赛成绩。

1 速度滑冰中的空气阻力

在进入今天的主题之前,先介绍一个原理,“相对运动原理”。这里举一个生活中的例子。当我们站立不动,遇到迎面来的大风时,会感觉到空气的作用力。相反,当我们在没有风的情况下奔跑,同样会感觉到空气阻碍我们前进的力。当人和风的相对速度相等,人受到空气的作用力也相等,这个原理在空气动力学中叫做“相对运动原理”。根据这个原理,我们在进行空气动力学分析时,采用物体不动、空气流动的形式,观察更直观,实验也更容易。

那么空气如何在物体表面产生阻力呢？我们以空气围绕一个静止圆柱体的流动为例,如图1 所示进行说明。这里显示了圆柱的横截面,对于任意一个小的区域(这里用红线进行标记),空气对物体表面的作用力可以分为两部分,一部分是沿着表面方向的空气摩擦力Ff,另一部分是垂直于表面方向上的空气压力Fp。

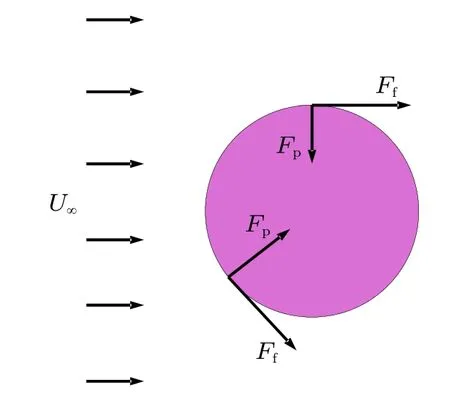
图1 空气围绕圆柱流动时的受力分析

1.1 摩擦阻力

摩擦阻力要从流体的基本物理性质之一,即黏性讲起。我们可以做一个简单的实验,往两个烧杯里分别倒入水和甘油,再用搅拌棒分别缓慢搅拌。先来搅拌水,发现能很轻松将水搅拌起来。再来看甘油,抬起搅拌棒,发现甘油能够沾到搅拌棒上,再进行搅拌,我们发现阻力较大。那么这是为什么呢？生活中的经验告诉我们,这是由于甘油更黏。流体对其内部相对运动的阻碍能力即为黏性,黏性用黏度系数来衡量。那么,黏性怎么产生对流动的阻碍呢？与固体和固体之间的相对运动可以产生摩擦力一样,流体内部层与层之间的相对运动也会产生摩擦力,这个摩擦力称为内摩擦力,阻碍流体运动。

1686 年英国科学家牛顿,通过实验验证了流体的内摩擦力定律。没错,这里的牛顿就是发现万有引力的大科学家牛顿。牛顿的内摩擦定律表明：相邻的两层流体之间摩擦力,与黏度系数、流体层之间的速度差、接触面积成正比,与流体层之间的距离成反比。流体包括了液体和气体,虽然一般气体的黏度比较小,比如空气,我们呼吸空气的时候不会费力。但在速度较高的时候还是会产生不可忽略的内摩擦力。图2 显示了空气流过圆柱上一个小区域时的速度分布。在圆柱表面上,由于空气有黏性,紧贴表面的这层流体粘附在表面上,空气的速度为零。而在远离表面的位置上,速度为来流速度。空气层与层之间存在相对速度,也就产生了内摩擦力。内摩擦力作用到壁面上,就产生了空气对壁面的摩擦力。

图2 空气流过圆柱上一个小区域时的速度分布

1.2 压差阻力

下面介绍一下压差阻力。如果对人体的形状进行简化,可以认为人体是由一些球体和圆柱体等形状组成。圆柱体是空气动力学中研究较深入的一种物体,运动员的手臂和腿都可以近似为圆柱体。通过演示风洞实验,可以观察到圆柱体周围的流动,看一下压差阻力是如何产生的。在风洞中,物体不动,以人工的方式产生气流,来模拟物体与空气的相对运动,是空气动力学实验最常用的工具之一。这里我们采用桌面大小的演示风洞,如图3(a) 所示。风洞的流速达到了13 m/s,与运动员在赛场上的平均速度接近。采用的圆柱模型的直径也与运动员小腿最细部位的直径接近,约为65 mm。这样能更真实地模拟赛场上的状态。因为空气是透明的,为了显示空气的流动,我们在风洞的进风口布置了超声波发生器,生成微小液滴组成的水雾。水雾会随着空气进入风洞,再通过片状的激光打亮这一片层上的微小液滴,来显示空气流动。

从图3(b) 所示的照片可以看到,空气从左向右流动。圆柱的迎风面上,流体沿着圆柱表面运动,到圆柱后面就脱离了圆柱面,产生了所谓的“流动分离” 现象。圆柱前面的空气流动受阻,速度降低,压力升高；圆柱后部的分离区域内的流动变得混乱,产生较前部小的压力；这样就在圆柱前后产生了压力差。对于运动的物体,前后的压力差产生了与运动方向相反的阻力,称为压差阻力。

图3

1.3 阻力系数

前面我们讲到,与空气相对运动的物体受到摩擦阻力和压差阻力,合起来就是空气阻力。在一定的流速条件下,物体所受到的空气阻力一般用阻力系数来衡量。阻力系数的公式为

其中CD表示阻力系数,FD表示空气阻力,ρ表示空气密度,U∞表示来流速度,A表示迎风面积。迎风面积指的是迎着风看过去,物体轮廓包围的面积。阻力系数一般由实验测量得到,也就是测量到空气阻力以后,除去其他的物理量。需要说明的是,在不同流速下阻力系数是变化的。但在一定流速范围内,数值变化不大,可认为是常数。

图4 所示为一些简单形状物体的空气阻力系数,在同样的流速和迎风面积下,我们前面讲的圆柱体,阻力系数为1.2,平板的阻力系数为2.0,这种类似水滴形的物体的压差阻力系数很小,为0.12。空气可以沿着物体从前端分开,经过平滑的过渡,在后端汇聚,有很小的分离区,压差阻力较小。由于流体流动的轨迹与物体的表面形状相似,这种形状的物体叫做流线体,例如鱼、机翼等都可称为流线体。而对于平板和圆柱体这一类非流线型物体,分离区较大,就会产生较大的压差阻力,因而阻力系数大,这一类物体称为钝体。

图4 简单形状物体的空气阻力系数

2 速度滑冰中的空气阻力

上面,我们了解了空气是如何在物体表面产生阻力的。下面,将介绍一下这些空气动力学原理是如何运用到速度滑冰项目中来帮助运动员减阻的。

2.1 服装减阻

我们观看比赛的时候看到运动员的服装是特制的紧身衣,紧身衣的一个重要功能就是减小空气阻力,其空气动力学设计成为影响成绩的重要因素。

根据牛顿给出的流体运动的内摩擦定律,我们知道,摩擦阻力受空气黏性、空气与运动员相对运动分布的影响,并与空气接触的表面积成正比。空气的黏性在固定的场馆下无法改变；相对运动分布取决于运动员的能力,也是基本无法改变。若要减小摩擦阻力,需要减小与空气的接触面积,即可以按照运动员体形定做紧身衣,让衣服紧贴身体。速滑运动员的服装很有弹性,可以贴近身体,有些部位的材质摸起来很光滑,已经有点像雨衣的面料,比我们平时穿的衣服要光滑。这是由于普通的布料表面都是有微观的结构(如西装),与光滑表面相比有更大的接触面积,在高速运动时会有较大摩擦阻力,所以需要采用更光滑材质来减小摩擦阻力。紧身衣同时也减小了迎风面积,减少了压差阻力。

但我们在观看比赛的时候,如果细心观察,可以看到运动员的紧身衣并不是所有表面都是光滑的,而是在前臂和小腿处拼接了一些粗糙的面料[6]。这是什么原因呢？下面我们还是以圆柱绕流这一个流动形式为例,来讲解其中的原理。从图5 中可以看出,当流速很小时,流体分层流动,互不干扰,称为层流。当流速增加会出现各种流动模式,当流速增加到很大时,产生了我们在前面提到的流动分离现象。因为在分离点之前流动还是层流状态,此时的流动分离称为“层流分离”。分离区域中有许多小漩涡,流体做不规则运动,这种流动称为湍流。若流速再提高,圆柱前方的流动从层流发展为湍流,分离点向后移动。因为在分离点之前流动是湍流状态,此时的流动分离称为“湍流分离”。实验发现,层流分离的分离角,也就是分离位置在圆周上的角度,约82◦；而湍流分离的分离角约120◦。也就是说,湍流抵抗分离,延缓了流动分离的发生,分离区域的面积明显减小。实验表明,这两个情况下的空气阻力系数分别为1.2 和0.3 左右,有4 倍的关系。

图5 圆柱绕流下的层流、层流分离和湍流分离

我们根据运动员的平均速度14 m/s,小腿平均直径0.1 m 进行分析,发现绕运动员小腿的空气流动属于层流分离的情况。如果我们想利用湍流分离来减小运动员阻力,需要提高运动员的速度,但14 m/s的平均滑行速度已经是运动员的极限了。那么,空气动力学里有没有其他方法,可以帮助运动员实现湍流分离来减阻呢？

答案是有的。空气动力学实验表明,在一定流动条件下,表面粗糙的圆柱可以将周围的层流扰乱,转变为湍流。也就是说,圆柱表面从光滑变粗糙后,可以使层流分离转变为湍流分离,降低阻力系数。在适当的粗糙程度下,阻力系数可以从1.2 降低到0.6 左右。这就是为什么有些运动员紧身衣小腿和前臂会拼接一些粗糙的面料。

我们在北京理工大学西山实验区中科研级别的风洞中探寻一下粗糙服装面料的减阻效果。我们通过实验记录了具有光滑和粗糙表面圆柱的高速摄影结果,如图6 所示。可以看到在粗糙表面圆柱的分离点向后移动,从圆柱最高点的前方移到了后方。这也是我们之前讲到的湍流抵抗分离,延缓了流动分离发生,也就是实现了减阻。需要注意的是,在速滑运动员小腿的流动条件下,阻力系数随着粗糙程度有先减小后增加的变化规律[7-8],需要选择合适的粗糙程度。同时,不同比赛赛程中,运动员的平均速度也有变化,同样的粗糙度可能出现低速时阻力系数小,高速时阻力系数大的情况。所以,使用粗糙表面减阻时,需要在空气动力学原理的指导下,与运动情况和比赛策略相结合,做权衡考虑[9]。

图6 不同表面圆柱的高速摄影结果

2.2 姿势减阻

上述我们了解到运动员们的服装设计也是很有讲究的,可以通过改变服装不同部位的粗糙程度来实现减阻的效果。这个因素属于外部因素,那对于运动员自身,是如何在行进过程中减小阻力的呢？根据前文空气阻力系数的定义,我们知道,空气阻力正比于空气密度、运动员速度的平方、迎风面积和阻力系数。空气的密度在固定的场馆下无法改变；运动员速度取决于运动员的能力,也是基本无法改变。而迎风面积和阻力系数可以根据姿势来改变。运动员可以通过改变姿势,一来减小迎风面积,二来可以使身体达到接近线型,减小阻力系数。图7(a) 显示了一个精细的运动员三维模型,通过定义4 个角度,可以表示运动员滑行的姿势。研究表明,躯干与地面的角度和大腿或小腿的角度越大,空气阻力越大。由于运动员在比赛中的姿势是改变的,在现在的技术水平下,躯干与地面的角度平均值为25◦。

起跑时身体基本直立,滑行时都会保持一个身体前倾的姿势。在比赛中,运动员会尽量将手臂背到后面,尽可能地减少迎风面积。而当运动员奋力冲刺时,躯干几乎达到水平状态,也就是与地面成0◦。我们通过3D 打印,制造了不同弯腰程度的速滑运动员模型。我们通过北京理工大学西山实验区的风洞实验室,研究了不同姿势对于运动员周围空气流动的影响。图7(b) 显示了模拟不同弯腰程度运动员周围空气流动的高速摄影画面。通过对比,我们可以看出,随着弯腰程度的增加,身后分离区域的面积减小。身体接近平行于地面的模型得到很小的分离区域。这种情况下,运动员模型受到的阻力也是最小的。

为了观测更多的流动细节和预测运动员受到的空气阻力的数值,我们在计算机上通过计算流体力学方法模拟了运动员采用4 种姿势时周围的空气流动情况。图7(c) 显示了不同弯腰程度的模拟结果,可以看出同样的空气流动吹过不同角度的模型后,模型身后的流动分离区域随角度减小而减小。当角度达到25◦和0◦时,分离区很小,且空气附着在运动员背部流动,也就是说运动员的身形更接近于流线型。这里红色代表压力高的区域,可以看出运动员身体前面的高压力区的面积,随着弯腰程度的增加而减小,压差阻力也随之减小。表1 为计算机模拟得到的运动员采用不同姿势时受到的空气阻力数据。迎风面面积随着弯腰程度增加而减小；不同情况的摩擦阻力均很小,只有一点几牛顿。而压差阻力方面,从三十几变化到十几牛顿。总的空气阻力方面,我们发现25◦和0◦时的阻力较45◦有明显下降。与45◦的情况相比,25◦和0◦时压差阻力下降了50% 左右。需要注意的是,保持0◦虽然能有最小的空气阻力,但运动员保持这个姿势会产生过多的体能消耗,所以,这个姿势多在冲刺时使用。

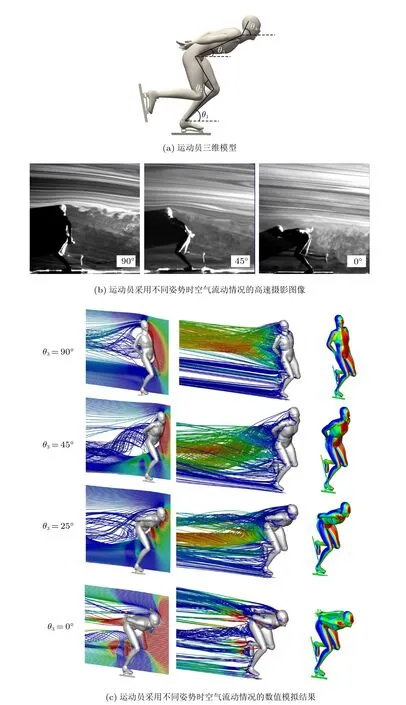
图7

表1 运动员采用不同姿势时受到的空气阻力

2.3 队列减阻

速度滑冰项目中团体追逐赛、集体出发赛都是前后跟随,成一个队列,有人在第一名领滑,有人在后面跟滑。有时候还会交换领滑位置。这又是怎样的一种策略呢？

我们再次通过西山实验区的风洞实验室中的实验,得到了并排和队列两种情况下的空气情况,如图8 所示。可以发现跟随的运动员处于前方运动员的分离区内,这样可以降低运动员模型受到的压差阻力。

图8 不同情况下空气流动情况的高速摄影图像

针对风洞实验,我们同样采用了计算机模拟得到了并排和队列两种形式的压力分布、流动情况(如图9 所示) 和阻力数据(如表2 和表3 所示)。可以看到,在并排情况下,各名运动员周围的流动情况基本类似。而在队列情况下,第一名运动员前面红色区域,也就是高压力区域较大,而第二、三名的高压力区域较小。这样后面的两名运动员的压差阻力较小。从流动情况来看,后面的运动员在前方运动员的分离区域内,所以身体前面的压力较低。下面我们看一下具体数据,并排的三名运动员中间和两边位置上的阻力基本相同。而队列中的跟滑运动员的阻力比领滑运动员少了近30%。

表2 运动员采用并排滑行姿势时受到的阻力情况

表3 运动员采用队列滑行姿势时受到的阻力情况

图9 运动员采用并排和队列滑行姿势时周围的空气流动情况

这就是为什么速滑中,运动员选择跟滑来减小体力消耗。在开头介绍的团体追逐赛中,领滑运动员需要克服的空气阻力较大,耗费的体能较大,会选择轮换位置,进行三名运动员之间的体力分配；集体出发赛中,领滑运动员会主动让出领滑位置,选择跟滑,节省体力,用于积分点和终点的冲刺。

3 结论

由本文我们可以看出空气动力学原理在速度滑冰中的应用。我们通过实验和计算机模拟具体了解了速度滑冰项目中如何减小运动员受到的空气阻力。通过改变服装的粗糙程度、运动员的滑行姿势、运动员的队列位置,都可以实现减阻。相信空气动力学理论和工程思想的结合,能为我国冬奥健儿提供所需的科技支持。

致谢感谢中央电视台科教频道《实验现场》栏目的大力支持,感谢刘青泉教授、霍波教授、周玲老师提供的帮助,感谢课题组研究生对本项目的实质贡献。