基于SSA–BP 方法土冻胀率影响因素敏感性分析
姚兆明 齐 健
(安徽理工大学土木建筑学院,安徽淮南 232001)
土体在低温条件下水分迁移产生的冻胀会对结构产生不利影响,为此,国内外学者进行了深入研究。研究成果有:提出Takashi 模型计算冻胀;运用数值计算方法计算冻胀力;考虑多因素对冻胀的综合影响,建立冻胀的统计预报模型;使用SPSS 软件建立的多元非线性回归模型预测冻胀[1-4]。
人工神经网络在岩土工程中的应用有: 模拟残积土在加载过程中的硬化、软化现象[5];建立人工冻土本构模型[6];预测加固工程的锚固力并分析各影响因素的敏感性[7];预测边坡稳定性,滑坡易发性[8-9];预测土体的冻胀量[10];利用反向传播算法(back propagation, BP) 网络确定岩石细观参数,结合颗粒流离元软件PFC2D 模拟应力−应变曲线[11];预测地表温度并将预测温度代入FEFLOW 模型对不同深度土壤温度进行模拟[12]。
本文提出一种基于麻雀搜索算法(sparrow search algorithm, SSA) 优化BP 神经网络的预测冻胀率模型,并结合多种优化方法提高预测精度,加快收敛速度,在此基础上研究人工冻土冻胀率影响因素敏感性。
1 人工冻土冻胀率预测
1.1 冻胀率试验
对甘肃地区三种不同性质土体进行冻胀率试验,土体物理化学性质见文献[4],采用外部补水的单向冻结方法。试验仪器主要包括保温系统、供水系统、温控系统、变形测量系统。在初始含水量、初始干重度、冻结速率、地下水位埋深、塑性指标、总离子含量范围给定情况下进行试验。由于文章使用小样本预测冻胀率,将各类不同性质土体分别试验,塑性指数IP和盐离子含量S是土体的自身特性,在同类型土中不属于变量,所以选取初始含水量、初始干重度、冻结速率、地下水位为输入量。考虑到我国以冻胀率来表示土体的冻胀敏感性,选择冻胀率为输出量。
1.2 SSA–BP 网络
BP 神经网络是一种多层前向型神经网络,通过寻找合适的网络结构和参数来完善从输入条件到做出决定的“反应链”,使网络结构能进行较高精度的预测[13-14]。BP 神经网络局限性:复杂的网络误差函数是多维空间曲面,网络训练过程中可能会陷入局部极小值而终止训练,未找到最小值。
SSA 是近年来新提出的一种种群优化算法。是将麻雀种群中个体分为生产者与拾荒者,以种群的采食与反捕食为基础设计的一种新型优化算法,具有较高的收敛性能和局部搜索能力[15]。SSA–BP 神经网络主要是对权值和阈值的优化,用SSA 的最优状态值来替代BP 神经网络里面的初始权值和初始阈值,减少迭代次数,使网络更快满足设计要求。
使用SSA–BP 网络预测土体冻胀率影响因素敏感性的基本步骤如下。
(2) 设置SSA–BP 网络参数;
(3) 使用SSA–BP 网络进行训练、测试、预测;
(4) 导出训练好的权值、阈值矩阵;
(5) 分别计算
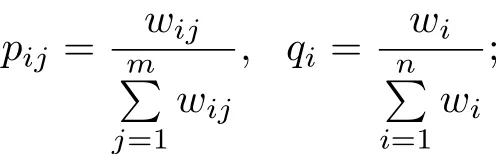
式中,wij为输入层第j个节点与隐含层第i个节点的连接权值,wi为隐含层第i个节点与输出量的连接权值,m为输入层节点数,n为隐含层节点数。pij为wij与隐含层第i个节点相关联的全部输入层连接权值和的比值,qi为wi与输出量相关联的全部隐含层连接权值和的比值。
1.3 网络模型参数的选择
由于单隐含层的拓扑结构适用于绝大多数条件下的非线性拟合,所以选用输入层– 隐含层– 输出层的三层网络拓扑结构。隐含层节点个数通常用确定,其中S为隐含层节点数,M为输入层节点数,N为输出层节点数,a为1~10 之间的整数值。为了使预测更精准,将a值选择范围从10 扩大至20,编写代码循环运行,选择误差最小的隐含层节点数进行预测。
结合试验数据确定传递函数分别为对数S 型传递函数和纯线性函数,并且通过多次尝试选取Levenberg–Marguardt BP 训练函数使误差减小。影响BP 神经网络预测精度的重要参数是学习速率η和动量因子α,学习速率η过小则收敛速率过慢、η过大容易修正过度而导致振荡发散。动量因子α过大存在丢失最小值风险,α较小可以避免局部极小值,但会使训练时间增加。使用二分法筛选发现η和α值均选为0.01 时误差最小。
“不纳入”,是指ACC系统不依赖DCS而完全独立,数据运算部分和逻辑控制部分均由ACC内部完成,与DCS无必然联系(个别重要的监视、报警信号可根据需要提供给全厂DCS系统);“部分纳入”,是指运算部分由DCS完成,逻辑控制部分交给ACC装置柜,两者相对独立又互相依托,共同组成了一套完整的焚烧炉控制系统;而“纳入DCS”,则是指焚烧炉控制系统不设置专门的ACC机柜和设施,数据运算、逻辑控制、画面组态等所有与焚烧炉相关的工作均由DCS来执行[2]。
1.4 SSA–BP 神经网络模型的训练
以砂壤土为例,在SSA–BP 神经网络模型中,训练集和测试集按占总体的75% 和25% 划分。BP 模型和SSA–BP 模型训练集数据的试验值、训练值和训练误差见表1,砂壤土测试集的预测结果见表2。

表1 训练集的试验值、训练值和训练误差Table 1 Test values, training values, and training errors for the training set
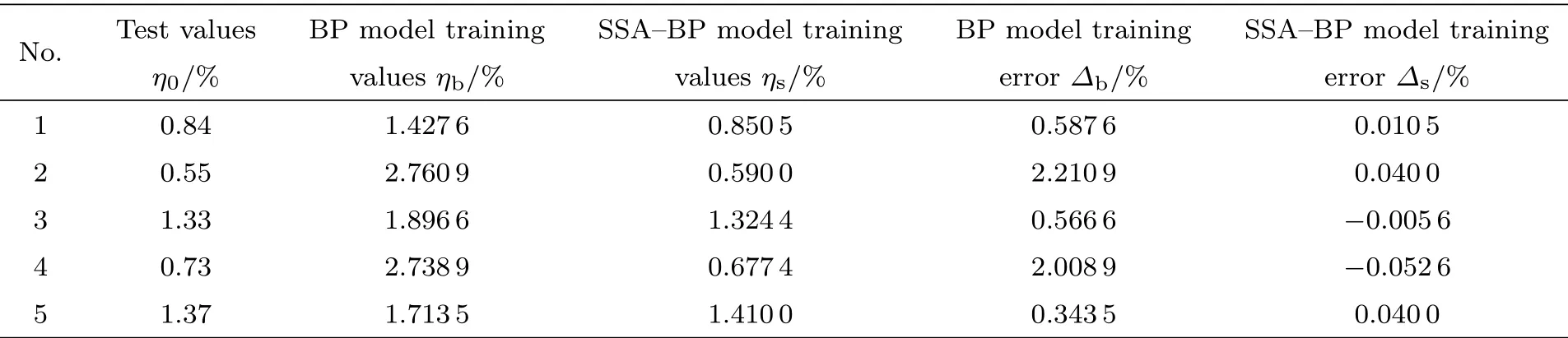
表2 测试集的试验值与预测值及误差Table 2 Test values, predicted values and errors of the test set
1.5 SSA–BP 神经网络模型的结果分析
图1 为砂壤土两种网络预测模型训练集的试验值与预测值对比散点图,结果显示SSA–BP 神经网络模型与实际值的拟合效果更优。
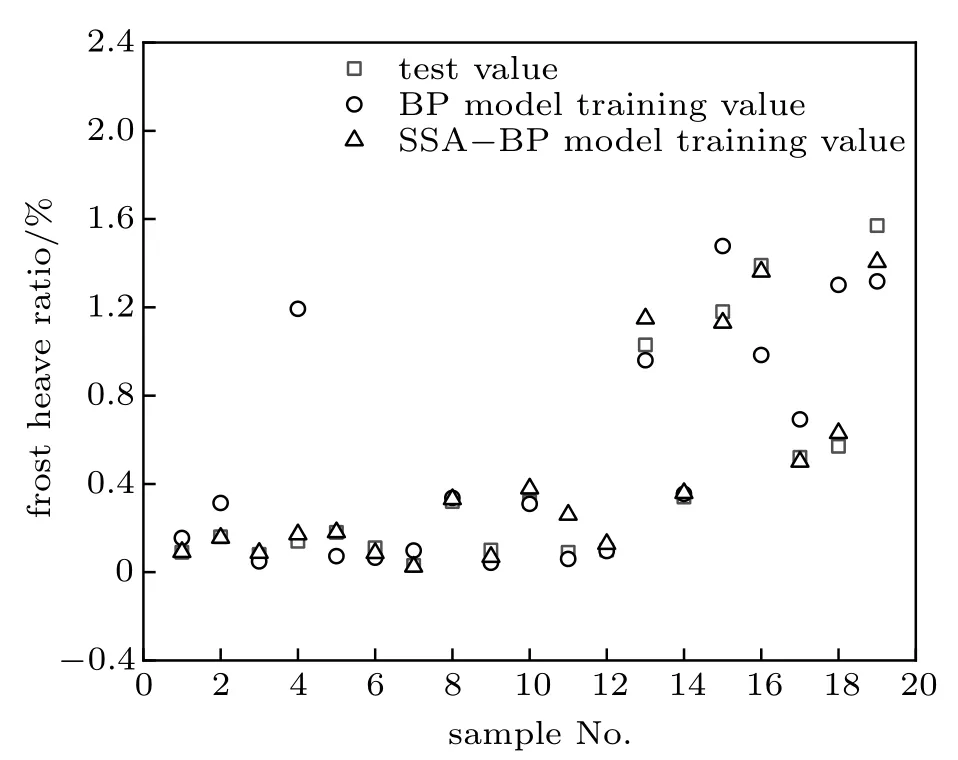
图1 两种网络预测模型训练集的试验值与预测值Fig.1 Experimental and predicted values for the training set of two network prediction models
从图2 砂壤土的试验值与预测值对比图中可以清晰看出,在使用SSA–BP 神经网络模型预测中样本4 的预测误差最大,达到−0.052 6,其余四个预测误差均在[−0.04,0.04]之间。较传统BP 神经网络精度至少提升十倍。SSA–BP 模型预测评价指标均方误差根为0.034 971,较BP 模型均方误差根1.393 4提升巨大,并且平均绝对百分比误差从BP 模型的162.96% 降至3.81%,SSA–BP 模型优化效果显著。

图2 砂壤土预测模型的试验值与预测值Fig.2 Test and predicted values of sandy loam prediction model
由图3 可知砂壤土使用SSA–BP 神经网络预测模型进行预测时,误差较传统BP 神经网络优化效果明显。砂壤土预测模型的误差整体控制在[−0.06,0.04] 之间,远小于 [−0.5,0.5],优化效果显著。

图3 砂壤土预测模型的误差Fig.3 Error of sandy loam prediction model
结合图4、图5 与表3 可知SSA 优化效果明显,计算结果表明:SSA–BP 模型能够较好地预测甘肃地区的砂壤土冻胀率,与此同时该模型对此区域的黏土与壤土冻胀率预测值与试验值也较为贴近,其误差均控制在[−0.5,0.5] 以内。
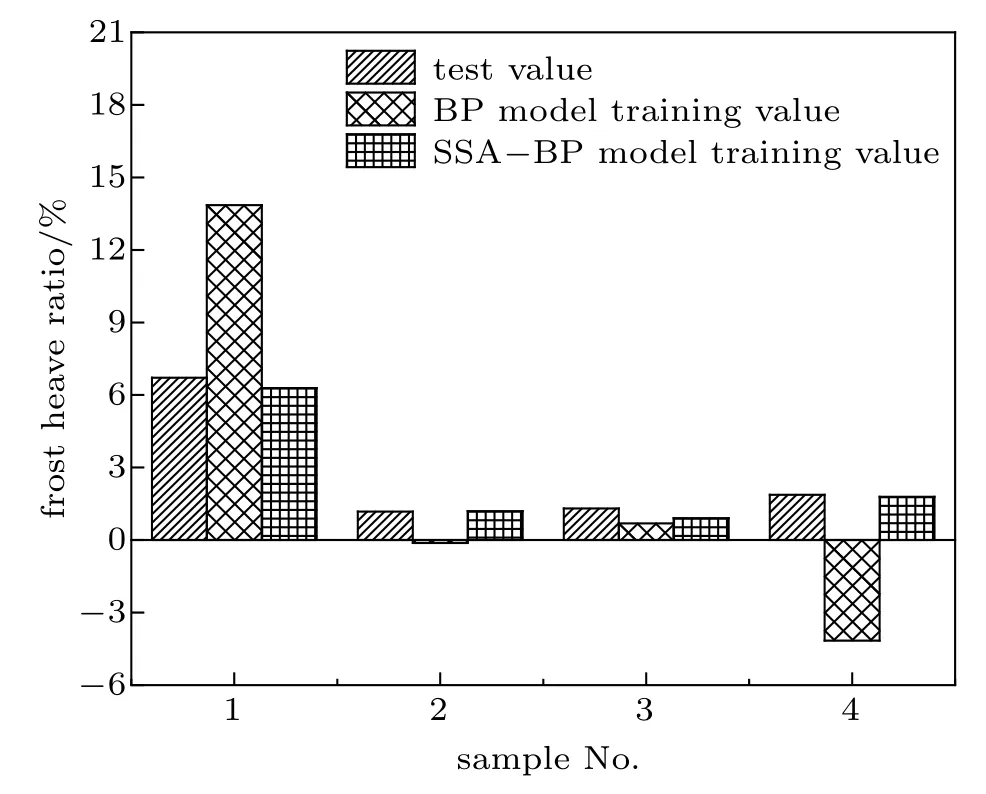
图4 黏土预测模型的试验值与预测值Fig.4 Test and predicted values of clay prediction model

图5 壤土预测模型的试验值与预测值Fig.5 Test and predicted values of loam prediction model

表3 黏土、壤土预测模型的误差Table 3 Error of prediction model for clay and loam
2 冻胀率影响因素敏感性分析
2.1 影响因素敏感性定义
影响因素敏感性通过定义无量纲形式的敏感性函数,使多个影响因素敏感性分析具有了可比性[16]。传统做法是设定一个基准状态,各影响因素取定值。再单独对各影响因素在取值范围内进行波动,观测结果波动程度及趋势。
神经网络模型中权值矩阵可以表明各个输入变量的敏感性大小,但需要综合考虑网络拓扑结构、归一化范围、激活函数等因素,过于繁琐。尝试将敏感性由权值矩阵简化为各影响因素权值占比,便于直观查看各个因素对冻胀率影响程度即影响因素敏感性
2.2 影响因素敏感性公式的应用
工程实例中地下水位Hw范围为0.43~0.95 m,初始含水率W范围为12.17%~28.6%,初始干容重γd范围为1.35~1.61 g/cm3,冻结速率Vf范围为2.95~9.68 cm/d。
应用SSA–BP 神经网络对甘肃地区三种土质建立三个独立预测模型,根据上述定义,计算各模型中因素对人工冻土敏感性Ki,如表4。

表4 各影响因素敏感性Table 4 Sensitivity of influencing factors
由表4 可知,冻胀率各影响因素敏感性中初始含水率的占比,在黏土、壤土与砂壤土中依次降低。土体冻胀的过程也是土中气态、液态水向冰转变的过程,在试验中黏土的塑限指数最大即初始含水量在塑限含水量与液限含水量之间试样最多,壤土和砂壤土塑限指数依次降低,与计算结果吻合。
黏土中初始含水量与初始干容重敏感性占比超过70% 是影响冻胀的主要因素,在人工冻土施工中可以外部控制水量和施加外部载荷降低冻胀率。壤土中初始含水量、冻结速率、初始干容重、地下水位线敏感性依次降低,初始含水量敏感性最大。影响砂壤土冻胀率的各因素中,冻结速率与地下水位线的影响超过一半,在工程中可以通过改变冻结温度和外部补水量来减少冻胀率。
综上可知,相同影响因素在不同土质中的敏感性不同,受土体的土质影响较大。
3 结论
本文使用SSA–BP 神经网络进行土体冻胀率预测,以甘肃地区土体冻胀率为例。选用影响试样冻胀率的四个主要参数即初始含水率、初始干容重、冻结速率、地下水位作为输入层,冻胀率为输出层,构建了三层SSA–BP 神经网络拓扑结构,得到以下结论。
(1)基于麻雀搜索算法优化权值与阈值,提高了BP 神经网络模型预测精度。对砂壤土、黏土、壤土的预测平均绝对误差均方误差根均小于0.3,较BP神经网络预测提升至少十倍。小样本预测针对不同土质均取得较好的预测结果,表明在寒区施工时为了减少冻害的影响,可以取试样进行试验获取参数,使用SSA–BP 神经网络进行预测,为工程安全高效施工提供一种选择的方案。
(2)提出新的影响因素敏感性公式,将各影响因素敏感性从神经网络繁杂的权值矩阵和阈值矩阵简化为数值。对砂壤土、壤土、黏土进行土体冻胀率敏感性分析,最敏感的影响因素分别是冻结速率、初始含水率、初始干容重,并且冻结速率、地下水位对不同土质冻胀率敏感性与土质塑限指数排序成反比。工程应用中,可根据不同实际情况采取针对措施减少冻胀危害。

