分段求解的弹簧操动机构断路器合闸优化设计

谭盛武，宋广民，解国林，奚延辉

（1.平高集团有限公司，河南 平顶山 467001；2.西安交通大学机械工程学院，陕西 西安 710049）

1 引言

断路器是电力系统中的重要器件之一，它主要通过动静触头的分、合闸动作来控制和保护电路，对于电力系统能否安全供电具有重要意义[1−2]。在众多的操动机构中，弹簧操动机构具有原理简单、开合迅速、可靠性高的特点，因而被广泛应用[3]。但是，弹簧操动机构的设计常常较为复杂[4−5]，尤其是核心零部件合闸凸轮，设计时不仅要考虑断路器的合闸行程曲线，而且更重要的是要使合闸输出特性与负载特性尽量匹配[6]。如果设计不佳，会造成断路器性能不良，即合闸不到位或者合闸时间、速度等不满足要求，还会产生较大冲击和振动，影响断路器的可靠性和寿命。

这些年来，我国的断路器行业经过这么多年的发展已经有了长足的进步。这一方面得益于基础理论、材料技术、生产设备的不断进步，另一方面通过和国外公司的合作引进先进的设计技术，这也促进了断路器向高质量、多品种的方向进步[7]。一大批研究者也投入到断路器的开发研究中来。文献[8]按输出力特性曲线进行凸轮设计，为凸轮的设计提出了一个新的思路和解决办法。文献[9]在断路器弹簧操动机构凸轮廓线的设计过程中，提出了一种负反馈优化设计方法，使动力特性准确匹配了负载特性。文献[10]结合摆动从动件滚子凸轮的设计方法建立了弹簧操动机构中凸轮机构设计的数学模型，并开发了基于遗传算法的凸轮轮廓曲线设计界面。在初步设计完成之后，其合闸速度、合闸时间、冲击等等条件是否符合设计要求还要通过检验，很多情况下还需要对其进行二次优化设计。并且由于现在对于断路器性能的要求越来越高，更多情况下需要对整个合闸过程进行优化，从而使优化变量变得更复杂、相关性更强，其求解难度大幅度上升，很多时候甚至可能找不到可行解。

这里阐述了一种合闸优化设计方法，建立了以操作功最小为优化目标，合闸弹簧刚度、合闸弹簧预压缩量和凸轮运动规律系数等为优化变量，刚合速度、初始结束边界条件和可靠合闸等为约束条件的优化数学模型。针对这种具有复杂的、相关性强的变量的优化模型提出了一种分段优化求解的方法，并采用遗传算法顺利完成求解，进而得到优化之后的合闸弹簧参数和凸轮廓线。最后，通过动力学仿真分析对优化结果进行了验证分析。

2 断路器合闸操作原理

断路器的合闸传动原理图，如图1所示。此时断路器的状态为分闸，合闸弹簧装置2储能完毕，下一步即将进行合闸操作。

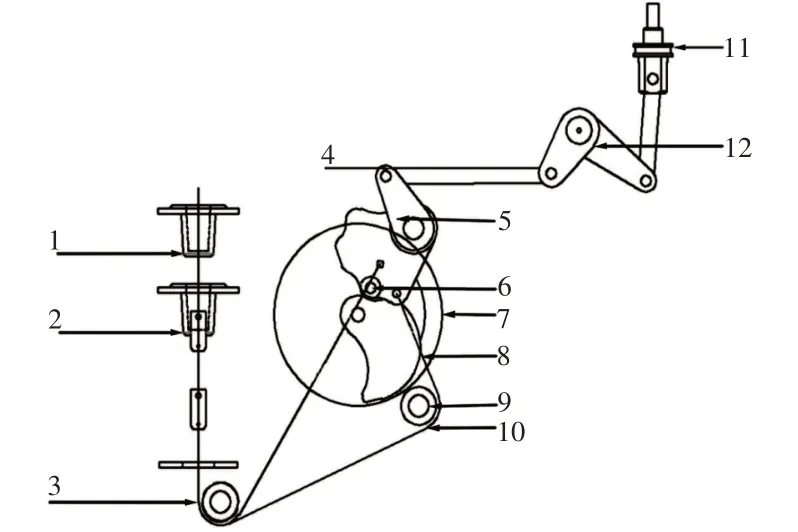
图1 合闸原理图Fig.1 Principle Diagram of Closing

合闸时，合闸锁闩打开，合闸弹簧装置2中的弹簧（未画出）释放能量，使上托盘向上运动，拉动合闸链条3运动，合闸链条3与飞轮盘7连接，因而带动飞轮盘7和与之同轴的合闸凸轮8逆时针转动，凸轮的转动推动主拐臂5顺时针旋转，进而借助机械拉杆4使输出拐臂12转动，逆时针旋转的拐臂12带动动触头连接头11及动触头（未画出）向上运动，达到合闸的目的。与此同时，主拐臂的顺时针旋转会带动分闸链条10运动，进而拉动分闸装置1中的上托盘向下运动压缩分闸弹簧，使分闸弹簧储能，为后续分闸做准备。

3 合闸优化数学模型

优化设计是在传统工程设计方法的基础上对构件尺寸进行选择、调整优化变量的大小，使系统工作在最佳状态。其数学模型由具有确定性的优化目标函数、优化变量和约束函数组成。

3.1 优化目标

合闸可靠性是断路器的一个重要指标，要保证断路器合闸的可靠性就要使机构在保证能完成合闸的基础上，其运动过程的能量足够小。这是由于过大的合闸能量不仅会导致设备的冲击和振动，降低其可靠性，还会影响其使用寿命。

鉴于以上考虑，借助操作功来表征合闸能量的大小，通过降低操作功来提高设备的寿命和改善运动特性[11]，所以采用合闸过程中的操作功最小为优化目标。

式中：kh、kf—合闸弹簧刚度和分闸弹簧刚度；Lhmax—合闸开始时合闸弹簧的压缩量；Lhmin—合闸结束时合闸弹簧的压缩量；Lfmin—合闸开始时分闸弹簧的压缩量；Lfmax—合闸结束时分闸弹簧的压缩量。

3.2 优化变量

影响断路器合闸运动特性的参数很多，但其中起主要作用的合闸弹簧、分闸弹簧和凸轮所对应的弹簧刚度、弹簧预压缩量和凸轮的运动规律的相关参数。但是由于分闸弹簧参数还影响分闸运动特性，在分闸设计阶段就设计完成，在合闸优化时不宜修改。所以需要通过优化合闸弹簧和凸轮的参数来达到优化合闸运动特性的目的。要通过凸轮来改变合闸特性就需要改变凸轮的运动规律。由于用多项式表达的从动件运动规律，容易保证高阶导数总是光滑和端点连续，所以采用多项式表达。通常，摆动从动件凸轮多项式运动规律可以写成：

式中：φ—从摆动从动件的转角；θ—凸轮转角。

综合考虑凸轮运动特性和加工难度，选择六次多项式表达，则：

另外，合闸弹簧的刚度和预压缩量也会影响合闸特性，所以可取凸轮运动规律表达式中的系数（C0∼C6）以及合闸弹簧的刚度kh，再加上合闸弹簧预压缩量l0为优化设计变量。

3.3 约束条件

约束条件是设计的限制条件，保证优化结果符合一定要求，约束条件是有关设计变量的等式或不等式。

3.3.1 刚合速度约束

刚合速度是合闸工况中的一个重要指标。要计算刚合速度就要计算操动机构在动触头处的等效质量。等效质量的表达式为：

式中：me—等效构件的等效质量；mj—活动构件上的质量；vj—第j个构件的质心速度；v—等效构件的速度；ωj—转动构件的角速度；Jj—转动构件的转动惯量；n—活动构件总数。

在得到动触头等效质量后，通过在刚合点处的能量守恒，即在考虑机构效率的条件下，合闸弹簧力做功减去阻力做功等于动触头的动能即可计算出刚合速度。

3.3.2 初始条件和结束条件约束

初始条件为，当凸轮转角θ为θmin时，从动件主拐臂的转角φ为φmin；结束条件为，当凸轮转角θ为θmax时，从动件主拐臂转角φ为φmax；另外，还要保证从动件的角速度ωφ>0，即主拐臂转角φ随凸轮转角θ的增加而单调递增。

3.3.3 可靠合闸约束条件

断路器要保证可靠合闸，所以在合闸终了时，动触头的速度不应该减为零，而应该还具有一定的速度。这就要求在合闸终了时，合闸弹簧做功大于分闸弹簧做功。

3.3.4 压力角约束

在凸轮机构中，压力角对机构的受力、运动有比较重要的影响，所以优化时还需要满足其压力角不超过45∘的条件。

在考虑约束条件时，可以先不考虑分闸时的压力角，这是由于在初始阶段压力角较大，将这部分也作为约束条件很可能无可行解，可将压力角作为优化后的校核。

4 优化求解

在建立好优化数学模型之后，就需要对其进行优化求解。目前搜索最优解的方法很多，大致可分为三大类数学规划法、优化准则法和仿生学方法。前文中所建立的模型为有约束非线性最小值优化模型。针对这种优化模型，尝试直接调用Matlab 中的fmincon 函数或遗传算法进行优化求解。但是由于优化变量中(C0∼C6)的强相关性，未能找到可行解。

虽然可以采用较低次的多项式来降低其相关性，比如三、四次多项式来表达凸轮的运动规律，但是这样就和实际的运动规律相差较大，也不满足在整个合闸范围内单调递增的条件。

为了保证运动规律的六次多项式的表达，同时也可以进行优化求解，我们提出一种先分段优化，再整体进行六次多项式拟合的优化求解的方法。我们将凸轮转角θ和主拐臂的转角φ之间函数φ=f(θ)分成三段，那么对于每一段就可以用次数低的多项式进行表达，再对三段分别进行优化。

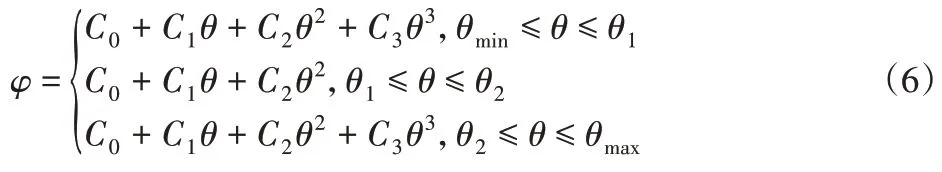
这样就会产生三个子优化模型，这三个子优化模型中，优化目标相同、优化变量只在φ=f(θ)的系数个数上有所不同。至于约束条件，只有中间段θ∈[θ1,θ2]需考虑刚合速度的约束条件。对于每一段的起始和结束边界条件要根据式（6）中的边界作相应改变。数学模型的优化求解流程图，如图2所示。

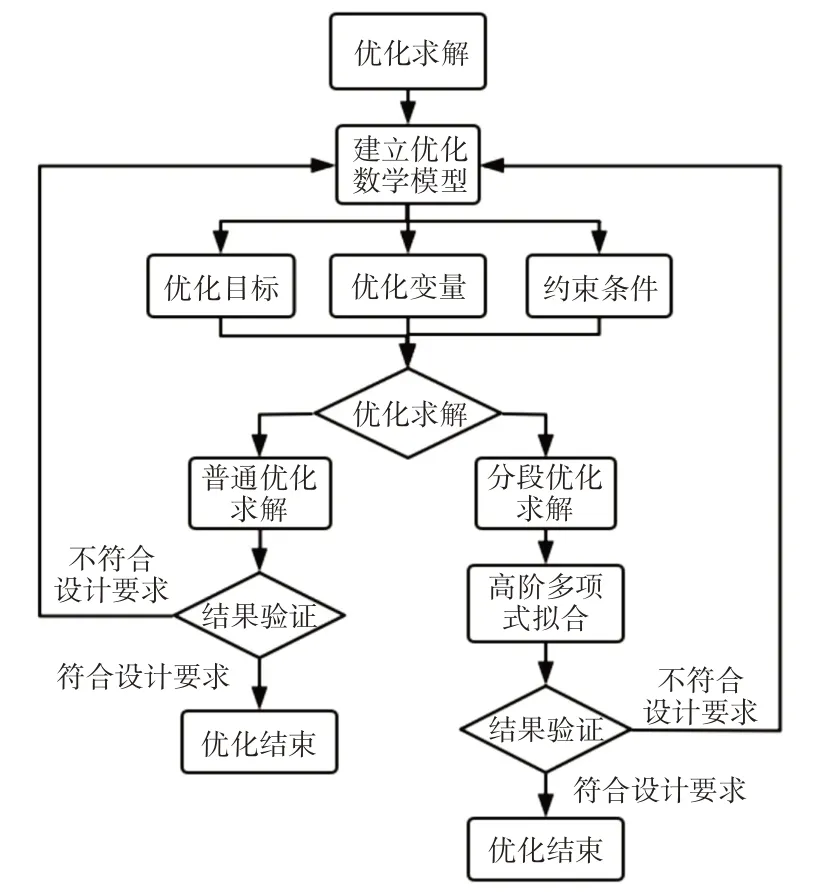
图2 优化求解流程图Fig.2 Optimization Solution Flowchart

进行分段之后就可以对三个子优化模型分别调用Matlab优化工具箱中的fmincon函数或遗传算法进行优化求解。求解之后将式（6）的三段表达式在θ∈[θmin,θmax]重新进行六次多项式的拟合，保证其运动规律的一阶、二阶连续。

5 优化结果

借助分段求解方法的优化结果，如表1所示。

表1 优化结果Tab.1 Optimization Results

将优化结果中的凸轮运动规律系数带入式（3）可以得到凸轮的运动规律曲线。再由摆动滚子从动件理论廓线方程：

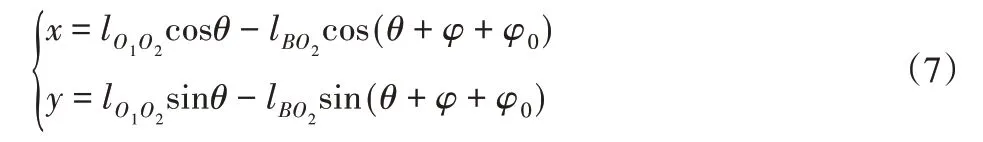
式中：lO1O2—凸轮转动中心到主拐臂转动中心的距离；lBO2—主拐臂转动中心到合闸滚子中心的距离；φ0—直线O1O2和BO2的初始夹角。由上式可得凸轮的理论廓线，将其与原理论廓线对比，如图3所示。

图3 凸轮优化前后理论廓线对比Fig.3 Comparison of Theoretical Profile Before and After Cam Optimization

6 分析与讨论

通过断路器的三维模型可建立断路器的动力学仿真模型，以此进行仿真分析可得到断路器的合闸运动特性曲线。并且通过更换优化后的凸轮，以及修改合闸弹簧的参数，还可以得到优化后的运动特性曲线。通过仿真分析得到的优化前后的动触头位移、速度曲线，如图4、图5所示。

图4 优化前后动触头位移曲线对比Fig.4 Comparison of Displacement Curve of Moving Contact Before and After Optimization

由图4 可以看出，优化前的位移曲线未达到触头的最大行程，并且迅速下降，这说明原模型合闸不到位。优化后的位移曲线达到了最大触头行程，并在之后一直保持在触头最大行程处，保证了可靠合闸。并且优化前后的合闸时间有所不同，优化后的合闸时间更长，曲线更为平缓，这是由于凸轮廓线的改变和优化后的合闸弹簧的预压缩量降低和最大压缩量均降低。

由图5可知，优化前的刚合速度为5.70m/s，优化后的刚合速度为5.41m/s，在保证合闸的情况下，合闸速度还有所降低，并满足技术要求，因而减小了断路器的冲击和振动。

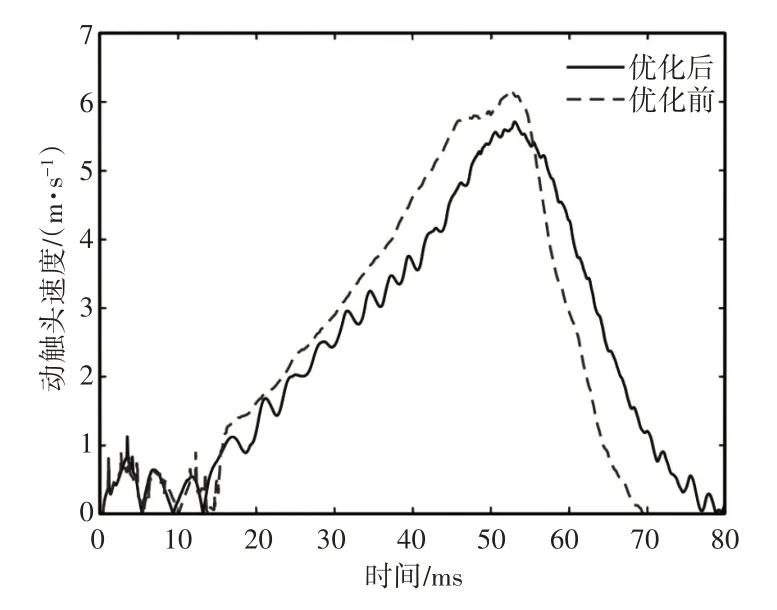
图5 优化前后动触头速度曲线对比Fig.5 Comparison of Speed Curves of Moving Contact Before and After Optimization

此外，从图6所示压力角曲线可以看出，合闸时，在凸轮转角为(10∘~180∘）的范围内，压力角都满足不超过45∘的约束条件。但在合闸初始阶段压力角较大，不难理解，初始阶段从动件和凸轮刚接触时，此时从动件速度方向和受力方向基本垂直，所以压力角较大，但这并不影响合闸。

图6 压力角曲线Fig.6 The Curve of Pressure Angle

7 结论

为了对断路器的合闸特性进行优化，建立了以操作功最小为目标，合闸弹簧刚度、凸轮运动规律系数等为优化变量，刚合速度、初始结束边界条件和可靠合闸等为约束条件的优化数学模型。通过分段优化的方法降低了部分优化变量之间的相关性，进而顺利完成求解。优化后的断路器使原本不能可靠合闸的断路器可靠合闸，并在可靠合闸的基础上，断路器操作功减小46.1%，刚合速度减小5.09%，提高了断路器的工作性能和可靠性。