高速三金片绣送片机构弹性动力学特性研究

刘光辉，周俊荣，余为洲，胡晨星

（五邑大学机电工程学院，广东 江门 529000）

1 引言

单金片绣金片规格尺寸适应性和多样性差、效率低，已无法满足金片绣装置多金片的发展趋势。诸多学者考虑装置可靠性和制造性，严格控制生产成本，得到了不同结构形式的多金片绣装置[1−5]。然而，随着电脑绣花机送片机构的日益复杂化，运转速度、自动化程度和精密程度的提高，送片机构高速下的弹性动力学问题日益突出，构件动应力大大增加，易导致磨损、噪声和疲劳破坏，且易产生动态运动误差。

目前针对高速三金片绣送片机构的弹性动力学分析极少涉及，文献[6]针对高速电脑绣花机横梁振动引起的断线率问题以及刺绣产品质量问题，对电脑绣花机横梁进行了模态分析和谐响应分析，获得了横梁的动态特性。文献[7]以某多头电脑绣花机刺布机构为研究对象，基于多体动力学原理，研究了刺布机构动力学特性，得到了各种结构参数对其动力学特性的影响。文献[8]推导了电脑刺绣机针杆机构动力学平衡方程式，得出了各构件支反力及平衡力矩的变化范围，分析了针杆机构的支反力特性。因此，对送片机构进行弹性动力学分析对于提高系统精度、可靠度和稳定性具有重要意义。

综合上述考虑，以一种新型高速三金片送片装置为对象，分析了送片机构的组成、工作原理和运动过程，并进行运动学仿真分析，验证该机构的运动学可行性。基于弹性动力学理论建立送片机构的弹性动力学数学模型，探究动态响应与特征参数的关系，为高速多金片绣送片机构的设计和优化提供参考。

2 高速三金片绣送片机构的组成与工作原理

创新型高速三金片送片机构的结构示意图，如图1所示，主要包括凸轮前后控制机构、曲柄滑块左右控制机构、金片选择离合机构、平行四杆送片机构、金片座和升降机构，各机构配合工作，完成金片输入与刺绣。

图1 高速三金片送片机构示意图Fig.1 Structure of Parallel Tinsel Embroidery Sheet Feeding Device Schematic

由于不同规格的金片具有不同的尺寸，在控制绣针位置时，需控制不同方向的位移，以保证绣针与金片孔中心对齐。凸轮前后控制机构采用凸轮机构实现切换金片时的步距调整，使金片中心在前后方向上始终与绣针下落的位置重合。曲柄滑块左右控制机构基于曲柄滑块机构的工作原理，采用切换电机驱动，用以控制送片机构的左右位移，并与凸轮前后控制机构配合控制送片机构的二维位置，保证绣针与金片孔中心对准。凸轮前后控制机构和曲柄滑块左右控制机构的示意图，如图2所示。

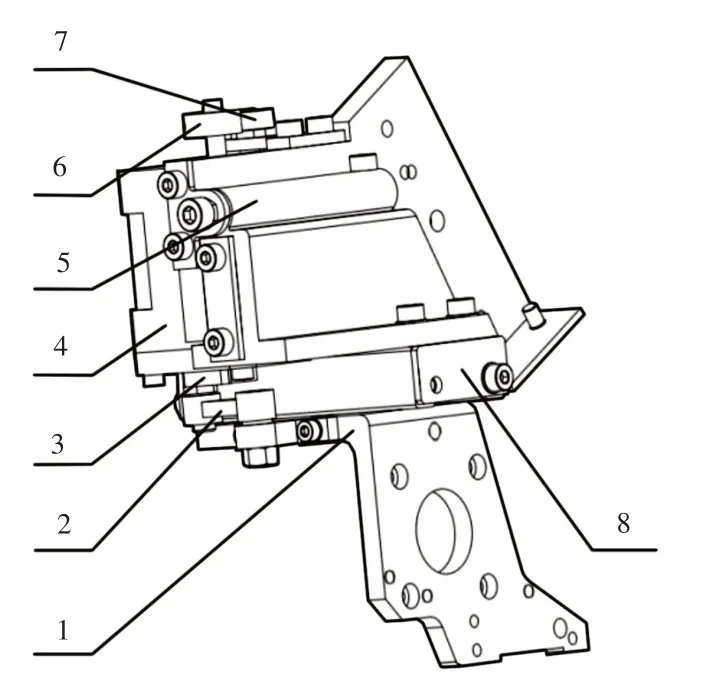
图2 控制机构示意图Fig.2 Structure of Control Mechanism Schematic

金片选择离合机构随曲柄滑块左右控制机构移动，控制金片选择的离合接头，可实现电机动力在三个平行布置的四杆送片机构之间的切换，进而实现三种规格金片的切换，如图3所示。平行四杆送片机构由三组并排布置的平行四杆机构组成，当离合滑扣与离合接头连接后便通过平行四杆送片机构传递电机动力以驱动送片执行端，实现送片动作。不同规格金片的并排输入，避免了“卡片”现象，提高了整机可靠性。机座的作用则是引导三种规格金片的输入和输出。

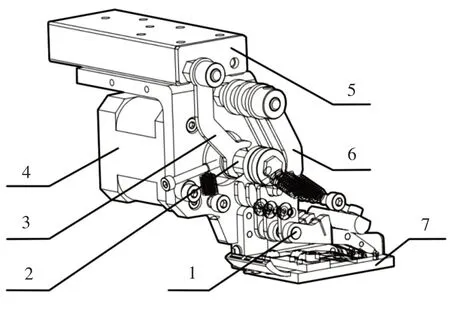
图3 离合与送片机构示意图Fig.3 Structure of Clutch and Sheet−Feeding Mechanism Schematic

升降机构主要由电动机、丝杠、导向槽和连接板组成，丝杠螺母与连接板联接，安装底板与针杆架联接，如图4所示。电动机驱动丝杠，使送片装置沿导向槽自动上升或下降，以实现绣框的自由运动。

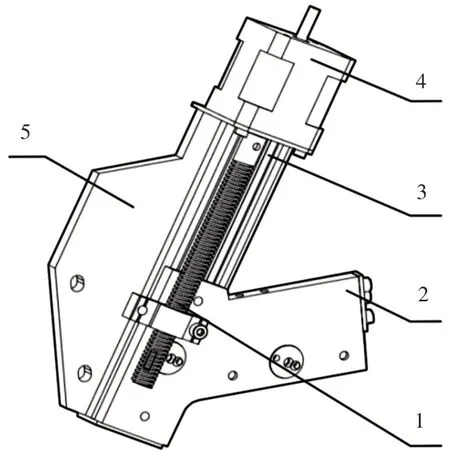
图4 升降机构示意图Fig.4 Structure of Lifting Schematic

3 送片机构运动学分析与参数设计

3.1 送片机构运动学建模

3.1.1 运动过程分析

为保证绣针与不同规格金片的孔中心对齐，高速三金片送片装置控制机构采用曲柄滑块机构和等加速等减速滚子从动件凸轮机构由同一切换电机驱动的方式，实现绣针的二维移动。控制机构简图，如图5所示。初始时刻绣针位于金片1中心孔D点，滑块中心处于极限位置A；曲柄和凸轮逆时针旋转θ1时，滑块沿X向移动s1，凸轮滚子从动件沿Y向移动H1，绣针沿轨迹S由D点运动至金片2中心孔E点。当曲柄和凸轮逆时针旋转180°−θ时，滑块沿X向移动s−s1至极限位置C，凸轮滚子从动件沿Y向移动H2至升程极限位置F，绣针沿轨迹S由E点运动至金片3中心孔F点。切换电机反向旋转，曲柄和凸轮顺时针旋转180°−θ，滑块沿−X向由C点运动至A点，滚子从动件沿−Y向运动，绣针沿轨迹S由F点移动至D点，以此循环。

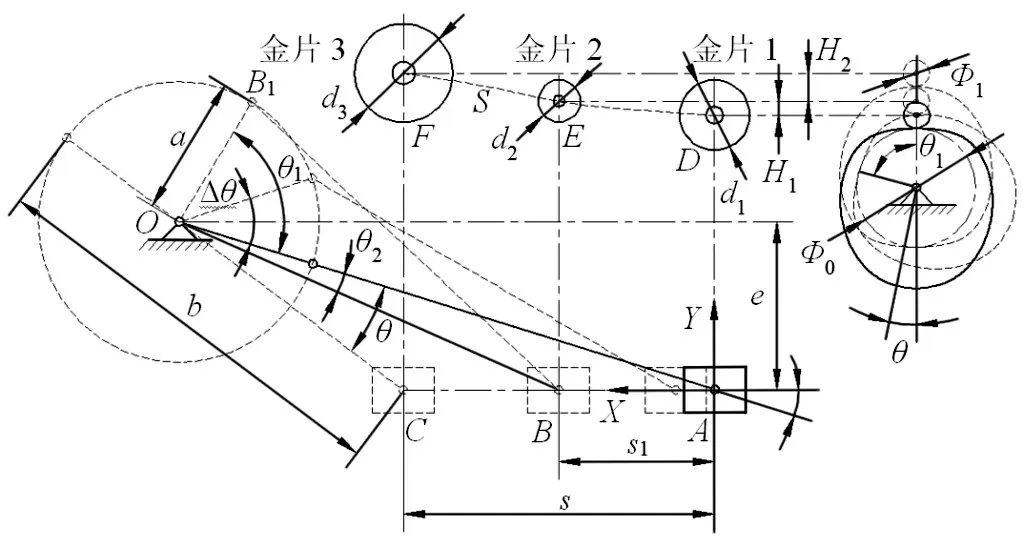
图5 送片装置控制机构运动简图Fig.5 Control Mechanism of Sheet−Feeding Device Schematic

3.1.2 运动学建模

设金片1、金片2和金片3的直径分别为d1、d2和d3，曲柄长度为a，连杆长度为b，e为偏置距离。凸轮基圆直径为Φ0，从动件滚子直径为Φ1。根据运动简图5中的几何关系可知：

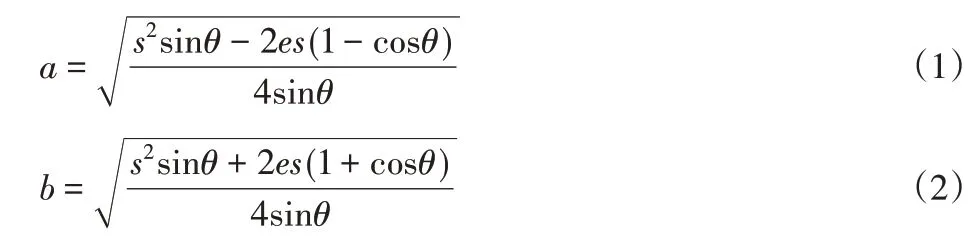
式中：s—滑块行程，mm；θ—极位夹角，°。

由余弦定理可得：

由偏置曲柄滑块机构的运动学方程可知滑块位移、速度和加速度与转角Δθ的关系分别为：

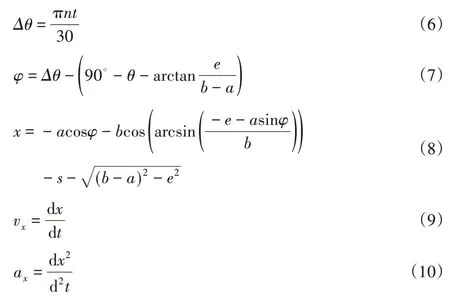
式中：t—时间，s；

n—曲柄和凸轮角速度，r/min。

滚子从动件凸轮机构的运动规律为h=h（t），h为从动件位移。当滚子从动件位移达到升程H时，时间为th，则等加速等减速凸轮机构加速阶段和减速阶段的理论位移、速度和加速度可分别表示为：

为使绣针与金片中心孔对正，当曲柄和凸轮转动至θ1时，滑块移动至s1，滚子从动件滚子中心运动至H1。经分析发现：当H1≤H2时，θ1≤180°−θ1−θ，等加速等减速凸轮滚子从动件由D点上升至E点的过程处于凸轮加速阶段；当H1>H2时，θ1>180°−θ1−θ，从动件由D点上升至E点的过程处于凸轮减速阶段。因此，有以下关系式：

为便于后续运动学特性的讨论，定义K1，K2用以表征金片规格尺寸和排列顺序：

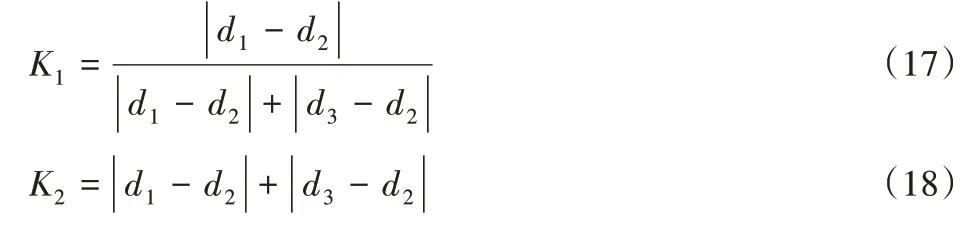
由式（1）~式（16）可求出三种不同规格直径d1，d2，d3下，特定滑块行程s，s1和凸轮基圆直径Φ0、从动件滚子直径Φ1的曲柄滑块机构和凸轮机构的结构参数，为后续送片机构运动学特性分析和参数设计提供理论数学模型。

3.2 送片机构运动学特性分析

为研究不同金片规格尺寸对送片机构运动学特性的影响机理，采用MATLAB编程对送片机构进行运动学仿真分析，得到不同金片规格尺寸的曲柄滑块机构和凸轮机构的主要参数，探究各影响因素与滑块和滚子从动件位移、速度和加速度之间的特征关系，为送片机构的参数设计提供依据。

取滑块行程s=30mm，s1=0.5，s=15mm，凸轮机构升程时间th=0.3s，给出了不同金片规格尺寸下曲柄滑块机构和凸轮机构的主要参数，如表1所示。

分析表1中所得结果可知：金片规格尺寸和排列顺序是影响送片装置控制机构结构参数的主要因素。其中，K1决定曲柄滑块机构结构参数，K1值越大，极位夹角θ、偏置距离e和连杆长度b越大，曲柄长度a越小；K2决定等加速等减速凸轮机构从动件升程H，且H与K2正相关。

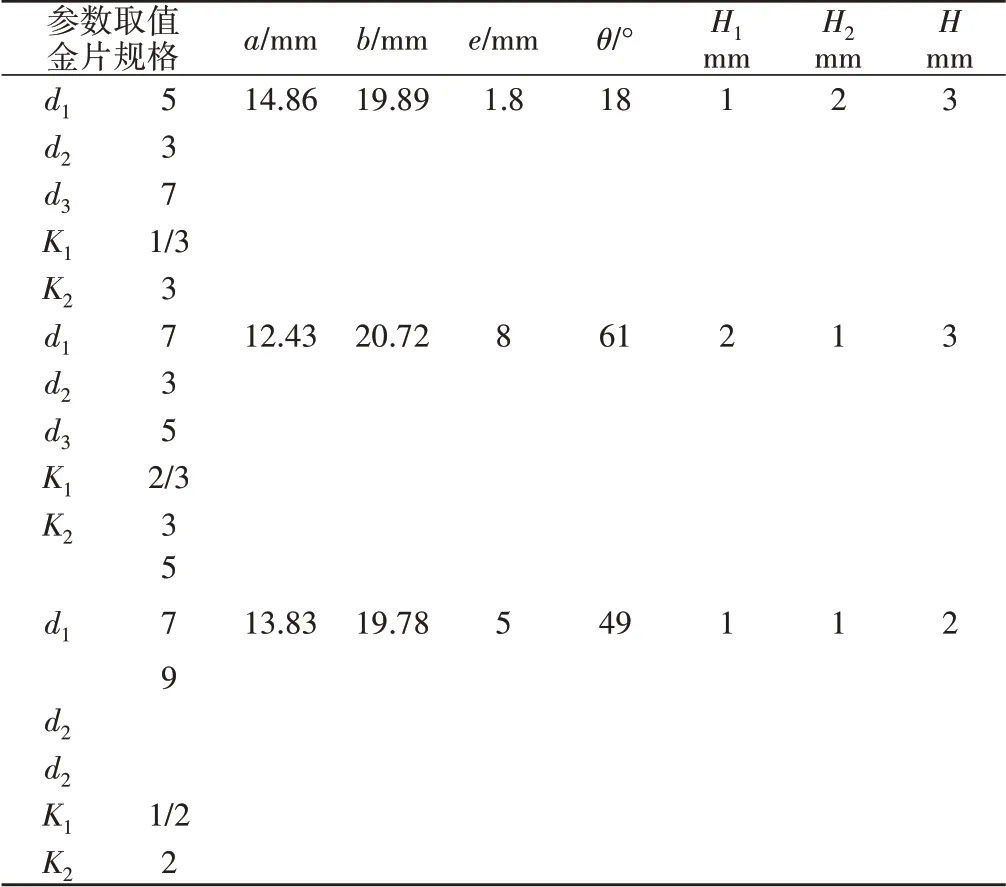
表1 不同金片规格尺寸的曲柄滑块机构和凸轮机构主要参数Tab.1 Main Parameters of Crank Slider and Cam Mech⁃anisms with Different Sizes of Tinsel Embroidery Sheet

不同金片规格和排列顺序下的送片装置曲柄滑块机构和凸轮机构从动件的位移、速度和加速度随时间的变化曲线图，如图6~图9所示。

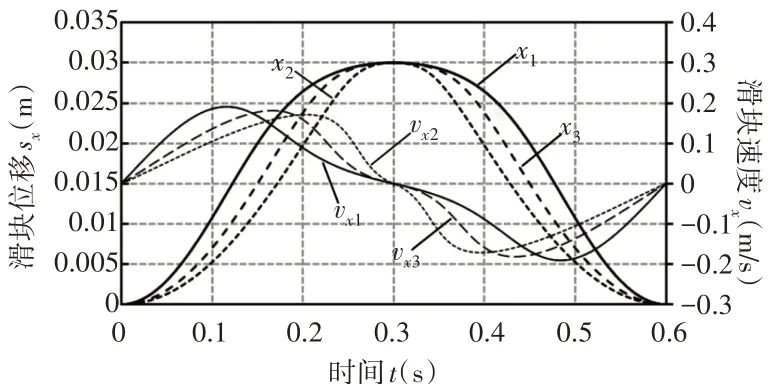
图6 不同金片规格尺寸的滑块位移和速度曲线Fig.6 Displacement and Velocity Curves of Sliders with Different Tinsel Embroidery Sheet Sizes

图7 不同金片规格尺寸的滑块加速度曲线Fig.7 Acceleration Curves of Sliders with Different Tinsel Embroidery Sheet Sizes

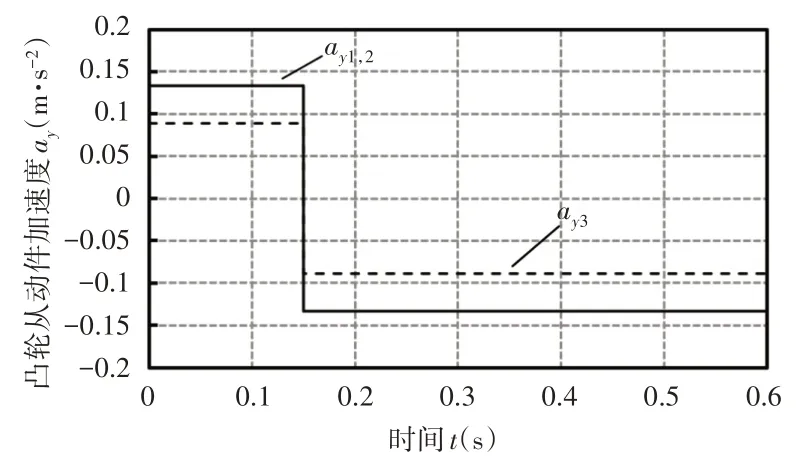
图9 不同金片规格尺寸的凸轮从动件加速度曲线Fig.9 Acceleration Curves of Cam Flower with Different Tinsel Embroidery Sheet Sizes

经分析发现：K1值越大，滑块最大绝对速度和绣针在E点沿X向的速度越小，最大速度对应的时间点越短。

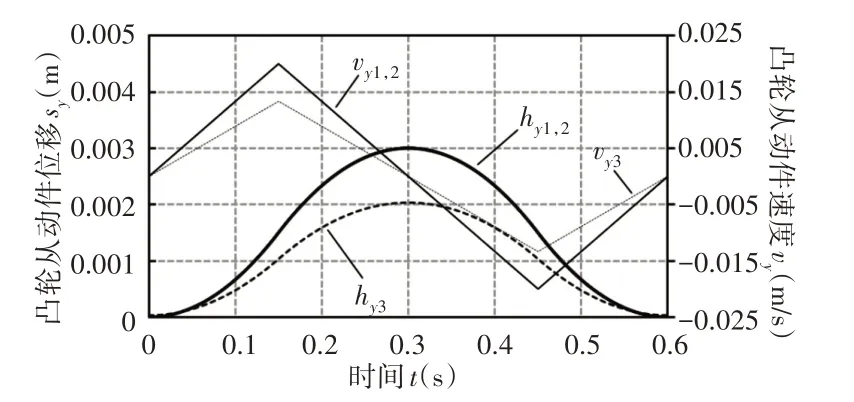
图8 不同金片规格尺寸的凸轮从动件位移和速度曲线Fig.8 Displacement and Velocity Curves of Cam Flower with Different Tinsel Embroidery Sheet Sizes

滑块最大绝对加速度和绣针在E点沿X向的加速度与K1正相关，首次出现最大加速度的的时间点越长。另外，当等加速等减速凸轮机构K2值相同时，凸轮轮廓曲线和滚子从动件的位移、速度和加速度随时间的变化规律相同，但绣针到达E点的时间不同；K2越大，从动件行程、速度和加速度越大，且绣针在E点沿Y向的速度越大。

3.3 送片机构参数设计

不失一般性，假设进行刺绣的三种金片规格分别为直径d1=5mm，d2=3mm和d3=7mm，则根据上面的运动学仿真结果和分析结论可知：曲柄长度a=14.9mm，连杆长度b=19.9mm，偏置距离e=1.8mm，滑块行程s=30mm，s1=0.5s=15mm，极位夹角θ=18°。凸轮从动件升程H=3mm，H1=1mm，H3=2mm，并取凸轮基圆直径Φ0=30mm，从动件滚子直径Φ1=10mm。

4 送片机构弹性动力学建模

为分析送片机构的动力学特性，在将曲柄、连杆和滑块视为刚体的情况下，基于单自由度动力学理论和集中参数模型，建立凸轮机构的弹性动力学模型，分析送片机构的动力学特性，得到了送片机构特征参数对动力学特性的影响机理，为送片机构的设计提供参考[9−10]。凸轮机构的等效单自由度动力学模型，如图10所示。

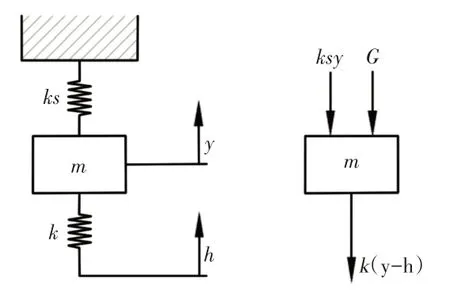
图10 凸轮机构的等效动力学模型Fig.10 Equivalent Dynamic Model of Cam Mechanism

外载荷G只引起静变形，振动分析时不予考虑。由于弹簧刚度ks远小于等效刚度k，因此可忽略弹簧刚度ks，并由牛顿第二定律可知：

式中：m—等效质量，kg；y—从动件末端质量的位移，mm；h—滚子从动件与等加速等减速凸轮接触点处的位移，即滚子从动件的理论位移，mm；ω1—系统基频，Hz。式（19）的无因次表达为：

式中：th—升程时间，s；ωn—系统固有频率，Hz。引入周期比λ：

对于等加速等减速凸轮机构加速阶段（0≤T≤1/2），式（21）可表示为：

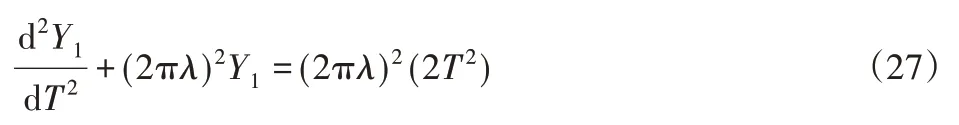
由初始条件Y（10）=0，Y1（′0）=0可求得，加速阶段的动态响应为：

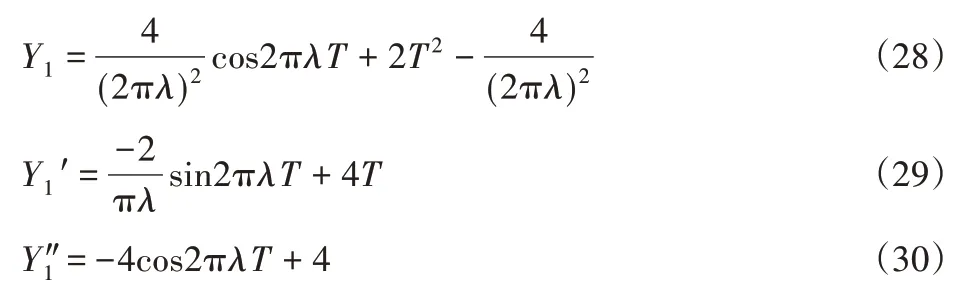
加速阶段绣针的动态响应可表示为：

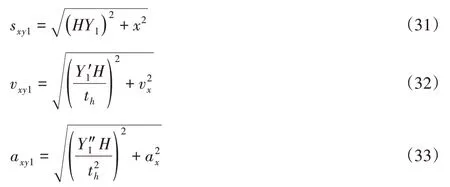
减速阶段（1/2≤T≤1），式（21）可表示为：

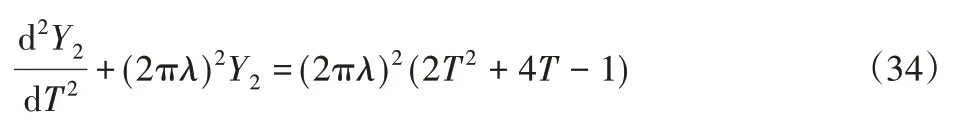
由初始条件Y（11/2）=Y（21/2），Y1（′1/2）=Y2（′1/2）可求得，

减速阶段的动态响应为：

减速阶段绣针的动态响应可表示为：

5 送片机构弹性动力学特性分析

以前文中所得的送片装置为算例，基于MATLAB/Simulink仿真平台，对送片机构的动力学特性进行了仿真分析，探究周期比λ对送片机构动态响应变化规律的影响机理。给出了不同周期比λ的凸轮机构滚子从动件的动态响应位移、速度和加速度曲线，如图11~图13所示。

图11 不同λ的凸轮从动件位移曲线Fig.11 Displacement Curves of Dynamic Response of Cam Follower with Different λ

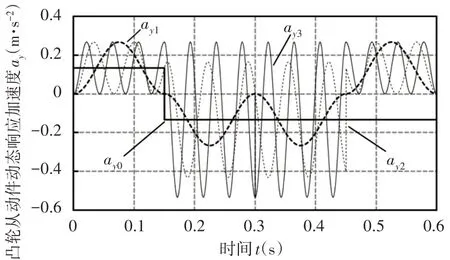
图13 不同λ的凸轮从动件动态响应加速度曲线Fig.13 Acceleration Curves of Dynamic Response of Cam Follower with Different λ

分析图11和图12中的动态响应曲线可知：凸轮从动件的动态响应位移、速度在理论位移、速度附近波动，且周期比λ值越小，即凸轮转速和绣针运行速度越高，绣针在D处、E处和F处停位S后的动态运动位移和速度误差越大，定位精度越低，越易出现修针与金片中心孔内壁接触的现象。

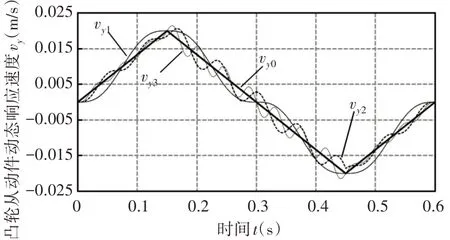
图12 不同λ的凸轮从动件动态响应速度曲线Fig.12 Velocity Curves of Dynamic Response of Cam Follower with Different λ

另外，从图12可以看出：动态响应加速度亦在理论加速度附近波动，并呈周期性变化。周期比λ值越小，响应加速度与理论加速度之间的动态误差越大，且响应加速度峰值大于理论加速度峰值，即凸轮的实际惯性力越大，使磨损、强度和噪声等方面的指标恶化。

由式（26）可得，周期比λ 与凸轮转速和系统的固有频率相关，凸轮转速越高或系统固有频率越小，周期比越小。因此，设计送片装置时，当凸轮转速或绣针运行速度较高时，保证系统刚度、强度、可制造性和轻量化等的同时，应增大系统固有频率以增大周期比，从而减小系统的动态响应，提高绣针的定位精度。

6 结论

这里分析了高速并排式三金片绣送片机构的组成、工作原理和运动过程，建立了送片机构的运动学数学模型，仿真分析了送片装置曲柄滑块机构和凸轮机构的运动学特性。

基于弹性动力学理论建立了送片机构的动力学数学模型，并采用MATLAB/Simulink 进行了仿真分析，得到了周期比对凸轮从动件动态响应的影响机理。得到以下结论：

（1）金片规格尺寸和排列顺序是影响送片装置控制机构结构参数和运动学特性的主要因素：K1值越大，极位夹角θ、偏置距离e和连杆长度b越大，曲柄长度a越小，H与K2正相关。另外，K1值越大，绣针在E点沿X向的速度越小，加速度越大。K2越大，凸轮机构从动件行程、速度和加速度越大，且绣针在E点沿Y向的速度越大。

（2）建立了送片的机构的弹性动力学数学模型，并进行了仿真分析，发现：凸轮从动件的动态响应位移、速度和加速度在理论值附近波动，且周期比越小，绣针的动态误差越大。

在设计送片机构时应提高系统刚度或降低凸轮转速，以增大周期比，从而减小动态响应误差，提高绣针的定位精度，对于三金片绣花机送片机构的设计与优化具有一定的指导意义和参考价值。