不同截面形式混凝土梁桥的竖向温度梯度效应分析

邢子寒，刘永健,2，闫新凯，王小龙，刘 江

(1. 长安大学公路学院，陕西西安 710064； 2. 长安大学公路大型结构安全教育部工程研究中心，陕西西安 710064； 3. 中交第二公路工程局有限公司，陕西西安 710065 )

0 引 言

混凝土梁桥的导热性能较差，日照作用和气温变化时梁体内部温度变化滞后，沿梁高方向会形成明显的竖向温度梯度[1-3]。简支梁桥在温度梯度作用下会产生自约束应力和变形，连续梁桥变形受到约束还会产生次生弯矩，温度效应严重时可能引起梁体开裂和支座脱空等病害[4-6]。

国内外对混凝土梁桥的温度场进行了大量实测和数值模拟研究，形成了多种竖向温度梯度模式。Priestley[7]基于实测和一维有限元分析，提出了“顶部5次抛物线+底部直线”的温度梯度分布形式，后来被新西兰规范[8]所采用。刘江等[9]在国内外多座桥梁上验证了该分布形式的适用性，通过大量的有限元计算给出了中国不同地区的顶部温差和底部温差取值。美国AASHTO规范[10]在Imsen等[11]研究的基础上，建议采用“顶部两折线+底部直线”的温度梯度分布形式，并根据太阳辐射分区确定温度基数取值。中国公路规范JTG D60—2015[12]将其简化为顶部两折线的分布形式，根据铺装层类型确定温度基数取值。欧洲Eurocode 1规范[13]沿用了英国BS5400规范[14]中三折线的分布形式，根据梁高和铺装层类型确定温度基数取值。刘兴法[15]基于简化的一维热传导理论，推导出温度梯度符合指数曲线分布，中国铁路规范[16]采纳了该分布模式。基于上述不同的竖向温度梯度模式，曾庆响等[17]将各温度梯度施加在箱梁二维平面有限元模型中，对比了横向效应计算结果，而未分析纵向效应。

当前对混凝土梁桥温度问题的研究多是围绕大跨箱梁的温度梯度模式确定和温度基数取值进行的[18-19]。雷笑等[20]实测了江苏省的一座混凝土箱梁桥的横截面温度场，按JTG D60—2015中的温度梯度模式确定竖向温度梯度，统计推算了温度基数的标准值、频遇值和准永久值。陶翀等[21]实测了浙江省的一座混凝土箱梁桥的横截面温度场，采用指数函数拟合竖向温度梯度，对顶面温差取值作了概率统计分析。Abid等[22]制作了一个混凝土箱梁的试验模型，测试了温度场和气象参数，建立了温度梯度的气象相关性预测公式。Song等[23]对广西省的一座连续刚构桥箱形截面的温度场进行了实测和数值模拟，在分析温度梯度的基础上计算了温度效应的日时程变化。Gu等[24]对江苏省一座连续刚构桥沿纵向不同位置处截面的温度场进行了实测和数值模拟，提出了不同高度截面的温度梯度，计算了温度效应，并与其他规范温度梯度计算的效应作了对比。中小跨混凝土梁桥在中国公路桥梁中占比非常大，其截面形式主要以空心板、T梁和小箱梁为主，此外它们也经常被用作大跨径拱桥、斜拉桥和悬索桥的桥道结构。跨径、梁高和截面形式的不同都可能导致温度效应的特点与大跨箱梁不一致。探讨温度效应对不同截面形式混凝土梁桥的影响将给桥梁设计和运营维护提供参考和启发。

在桥梁健康监测数据中温度效应相关信息占有很大比重，对有用信息的提取会产生较大干扰[25-26]。混凝土梁桥在运营过程中其效应的变化主要来自于汽车和温度作用，温度作用包括均匀温度和温度梯度，其中温度梯度引起的梁体挠度和应力变化会给监测结果带来干扰。当前考虑温度效应的桥梁健康监测研究主要是在大跨径索支撑桥梁中进行温度效应的分离[27-28]，但是近年来健康监测系统在中小跨混凝土梁桥中的应用也越来越多[29]，分析混凝土梁桥中温度梯度效应与汽车效应的比例关系，明确温度作用的影响程度，将有助于获取有用的结构监测信息。

因此，本文在总结混凝土梁桥典型的竖向温度梯度模式的基础上，从梯度曲线形式和温度基数取值两方面分析了不同的温度梯度计算引起的温度效应的差异，然后以《公路桥梁通用图》[30]中的中小跨径混凝土梁桥为研究重点，选取了几座代表性的大跨径混凝土箱梁桥进行比较，计算了竖向温度梯度效应，与自重和汽车作用产生的效应进行了对比，一定程度上揭示了温度作用对不同截面形式混凝土梁桥的影响程度。

1 温度梯度模式

1.1 几种典型的温度梯度模式

中国公路规范JTG D60—2015[12]中的混凝土梁桥的竖向温度梯度如图1(a)所示，其中T1、T2分别为梁顶和距梁顶10 cm处的温度，h为梁高，A为温度梯度的影响深度。正温度梯度采用顶部两折线的形式，负温度梯度为正温度梯度的-0.5倍。温度基数T1、T2由桥面铺装层类型确定，10 cm厚沥青混凝土铺装层的温度基数取值如表1所示。

中国铁路规范TB 10092—2017[16]中给出的混凝土梁桥竖向温度梯度如图1(b)所示，其中y为距梁顶的距离。正温度梯度采用指数曲线的形式，对梁高方向的负温度梯度未作规定。温度基数T1由桥梁所在地区的纬度、大气透明度以及桥面铺装类型确定，标准设计下的温度基数取值如表1所示。

欧洲Eurocode 1规范[13]中给出的温度梯度如图1(c)所示，其中T1、T2、T3、T4为梁截面不同高度处的温度。正温度梯度采用“顶部两折线+底部直线”的形式，负温度梯度采用顶、底部均为两折线的形式。温度基数T1、T2、T3、T4由梁高和铺装层类型共同确定，1.5 m梁高和10 cm厚铺装层的温度基数取值如表1所示。

新西兰规范[8]中给出的温度梯度如图1(d)所示，其中T2为梁底的温度。正温度梯度采用“顶部5次抛物线+底部直线”的形式，负温度梯度采用顶部直线的形式，温度基数T1、T2由桥梁所在地区确定，内陆地区的温度基数取值如表1所示。

美国AASHTO规范[10]中给出的温度梯度如图1(e)所示，其中T3为梁底处的温度。正温度梯度采用“顶部两折线+底部直线”的形式，但是截面下缘温度T3在未作实际调研时一般取0 ℃，最高不超过2.8 ℃。负温度梯度在未进行桥面铺装时为正温度梯度的-0.3倍，在采用沥青铺装时为正温度梯度的-0.2倍。温度基数T1、T2、T3由桥梁所在地理分区确定，分区Ⅰ的温度基数取值如表1所示。

图1 竖向温度梯度模式Fig.1 Patterns of Vertical Temperature Gradient

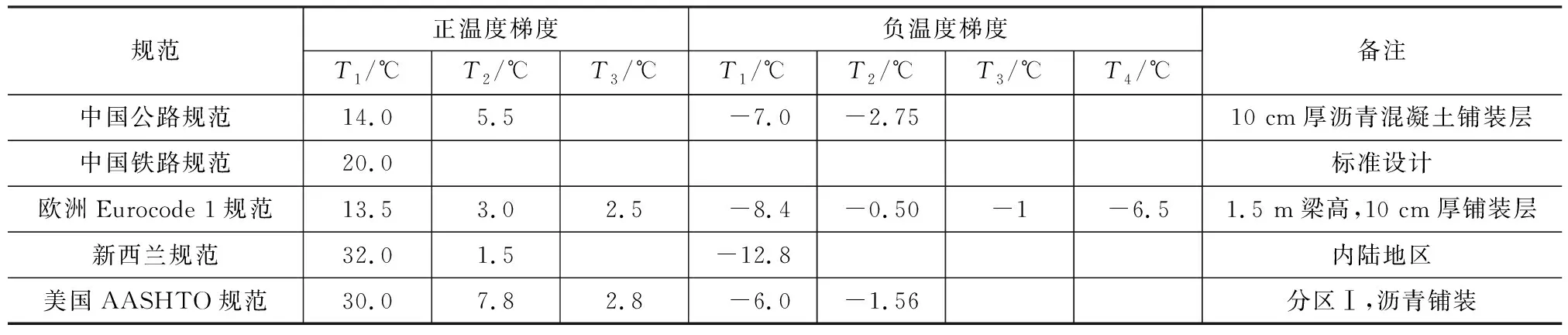
表1 温度梯度基数取值Table 1 Base Values of Temperature Gradient

通过上述分析可以看到，不同规范中温度梯度的曲线形式和温度基数取值有较大差异，这可能是测试或模拟的桥型、地域环境、分析方法以及简化思路等方面的差异所导致的。本文下节将从梯度曲线形式和温度基数取值2个方面分析它们对温度效应计算结果的影响。由于负温度梯度一般是将正温度梯度按一定比例折减考虑，折减系数不超过-0.5，因此本文后续仅对竖向正温度梯度模式和效应进行分析。

1.2 不同温度梯度模式计算效应差异的机理性分析

1.2.1 梯度曲线形式

不同国家和行业规范中给出的混凝土梁桥的竖向正温度梯度主要有4类曲线形式：两折线[12]、三折线[10,13-14]、指数曲线[16]、“5次抛物线+底部直线”[8]。为了对比梯度曲线形式对温度效应计算结果的影响，先保证温度基数一致，以顶部温差14 ℃为基准，其他的温度基数根据表1中取值按比例计算，计算的温度梯度如图2所示。从图2可以看到：①两折线和三折线中顶部温差的影响深度为0.4 m，文献[31]将距离每下降1 cm温度变化开始小于0.1 ℃的深度定义为顶部温差的影响深度，按此定义，指数曲线和“5次抛物线+底部直线”中顶部温差的影响深度约为0.8 m；②三折线和“5次抛物线+底部直线”中考虑了地面反射太阳辐射引起的截面底部升温段。

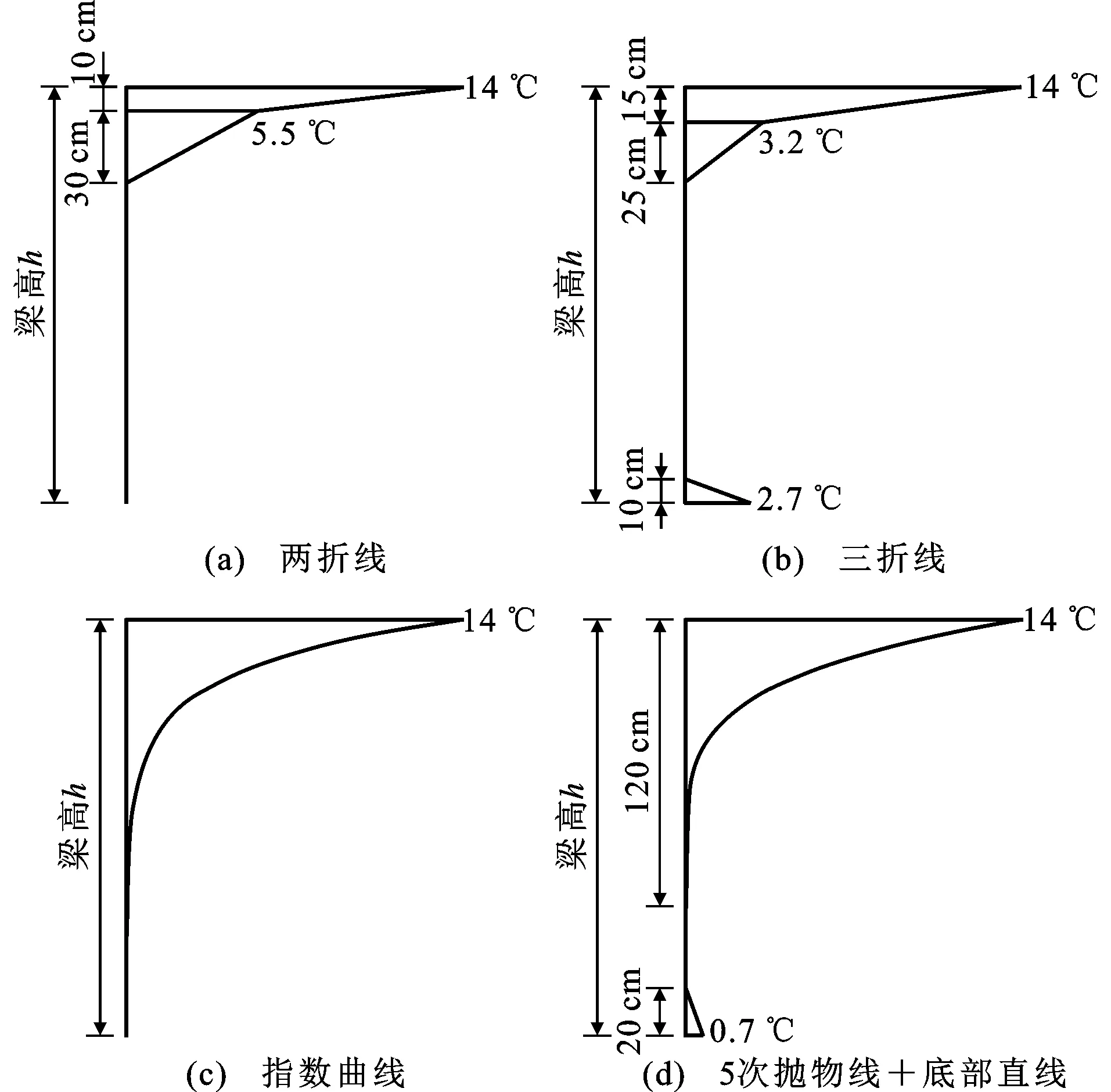
图2 不同曲线形式的竖向温度梯度Fig.2 Vertical Temperature Gradient with Different Curve Types

以40 m跨径的简支T梁桥和“67 m+122 m+67 m”跨径组合的连续箱梁桥为对象，其标准截面如图3所示，在标准截面上施加图2中的温度梯度作用，计算截面挠曲变形曲率和自约束应力[32-33]。

图3 标准截面(单位：cm)Fig.3 Standard Cross-sections (Unit:cm)

不同温度梯度曲线计算的截面弯曲变形如图4所示。从图4可以看到：无论是T梁还是箱梁，两折线与三折线引起的变形相近，指数曲线与“5次抛物线+底部直线”引起的变形相近；因为顶部温差的影响范围更深，指数曲线和“5次抛物线+底部直线”引起的弯曲变形更大，对于T梁是两折线和三折线引起变形的约1.3倍，对于箱梁是两折线和三折线引起变形的约1.5倍；对于连续梁桥，变形受到约束，指数曲线和“5次抛物线+底部直线”将引起更大的次生弯矩。

图4 不同温度梯度曲线计算的截面弯曲变形Fig.4 Bending Deformations of Cross-sections Calculated by Different Temperature Gradient Curves

不同温度梯度曲线计算的温度自应力如图5所示。从图5可以看到，各梯度曲线均在截面顶部和底部一定范围内产生自压应力，在截面中部产生自拉应力。无论是T梁还是箱梁，不同的梯度曲线计算的自应力存在一定的差异。两折线和三折线引起的截面上缘自压应力为指数曲线和“5次抛物线+底部直线”的约1.3倍；两折线和三折线引起的最大自拉应力在距截面上缘0.4 m处，指数曲线和“5次抛物线+底部直线”引起的最大自拉应力在距截面上缘约0.23倍的梁高处，“5次抛物线+底部直线”引起的自拉应力比其他曲线大0.15～0.4 MPa。因为考虑了底部升温段，三折线和“5次抛物线+底部直线”引起的截面下缘自压应力更大，三折线中底部温度基数取值较大，引起的压应力是两折线和指数曲线的2倍～3倍，“5次抛物线+底部直线”中底部温度基数取值很小，但引起的压应力也是两折线和指数曲线的1.25倍～1.8倍。

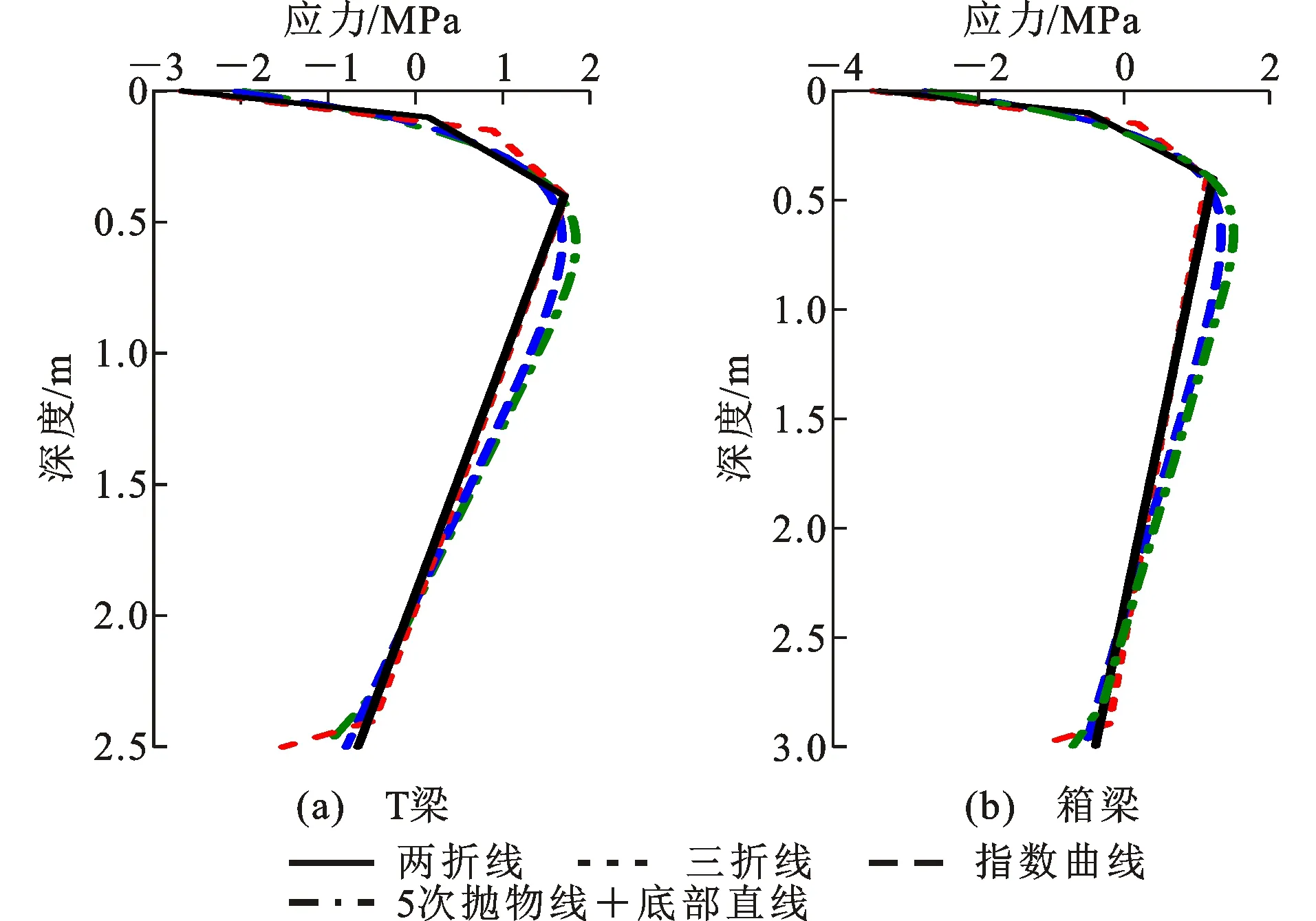
图5 不同温度梯度曲线计算的自应力Fig.5 Self-equilibrium Stresses Calculated by Different Temperature Gradient Curves

1.2.2 温度基数取值

中国公路规范JTG D60—2015中两折线形式的温度梯度根据桥面铺装层类型确定温度基数取值，如图6(a)所示，文献[9]中“5次抛物线+底部直线”形式的温度梯度根据桥梁所在中国地区确定温度基数取值，如图6(b)所示。以40 m跨径的简支T梁桥和“67 m+122 m+67 m”跨径组合的连续箱梁桥为对象，分别计算在这两类温度梯度作用下，温度基数取不同值时的温度效应。

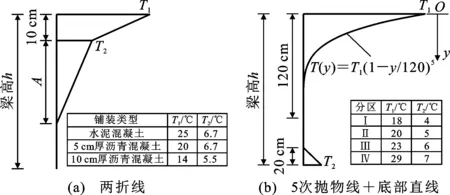
图6 不同温度基数的竖向温度梯度Fig.6 Vertical Temperature Gradient with Different Temperature Temperature Base Values

两折线形式温度梯度计算的温度效应如图7所示，连续箱梁桥墩顶截面由于梁高较高以及截面下缘自压应力和次拉应力相互抵消，所以应力很小。从图7可以看到，无论是简支T梁桥还是连续箱梁桥，随着温度基数增大，桥梁变形和截面应力均增加，其中水泥混凝土铺装下截面上缘应力为10 cm厚沥青混凝土铺装下的1.8倍～2.0倍，跨中挠度和截面下缘应力约为10 cm厚沥青混凝土铺装下的1.5倍。“5次抛物线+底部直线”形式温度梯度计算的温度效应如图8所示，可以看出，无论是简支T梁桥还是连续箱梁桥，从分区Ⅳ到分区Ⅰ随着温度基数的增大，桥梁变形和应力均增加。分区Ⅳ的温度效应约为分区Ⅰ的1.6倍，该比例与顶部温度T1在分区Ⅳ和分区Ⅰ的比值相近，表明顶部温度起主导作用。

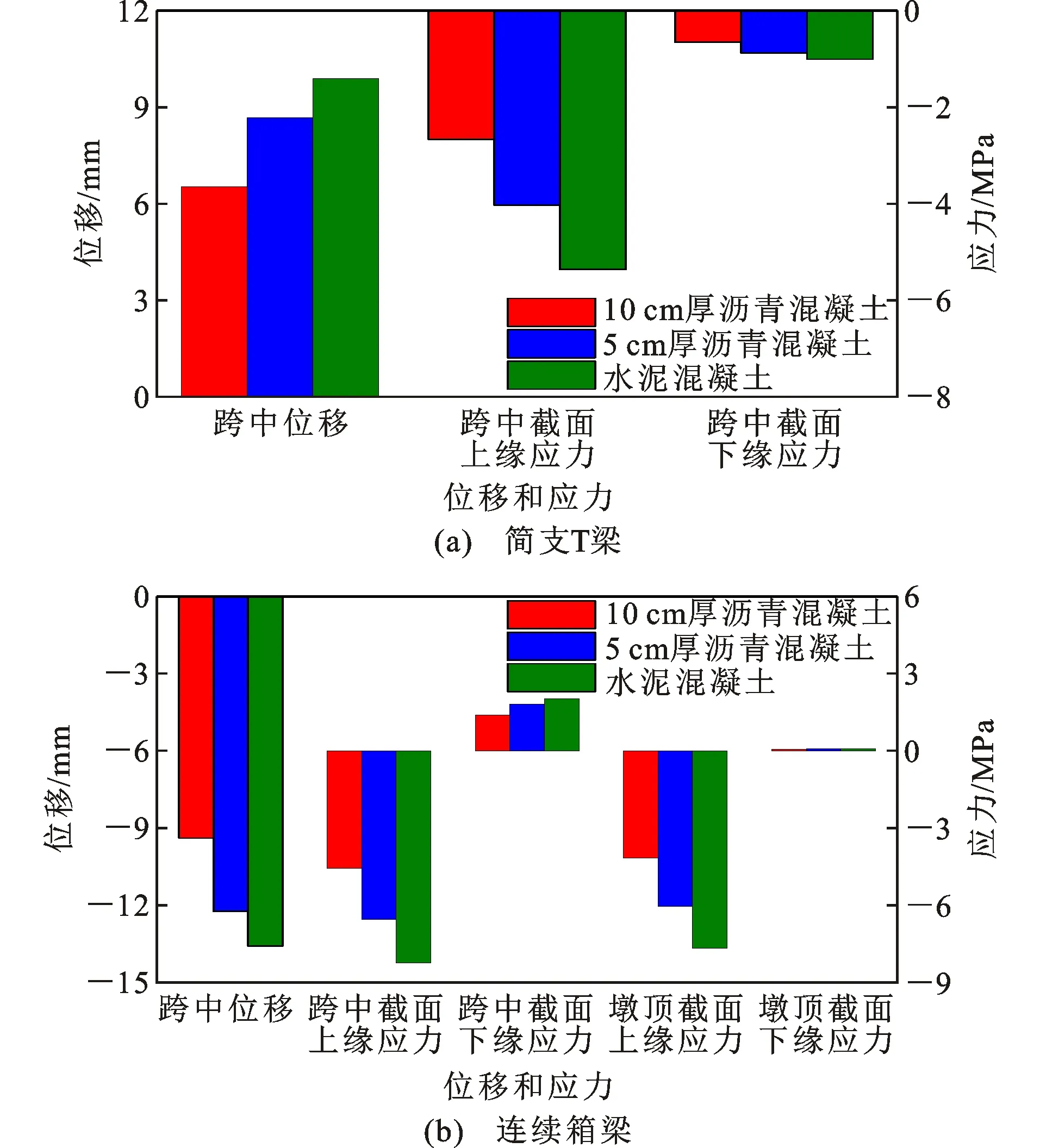
图7 两折线计算的温度效应Fig.7 Temperature Effects Calculated by Two Broken Lines

图8 “5次抛物线+底部直线”计算的温度效应Fig.8 Temperature Effects Calculated by “5th Parabola + Bottom Line”

2 作用效应比例关系

2.1 效应比例系数

2.1.1 混凝土梁桥

以2008版通用图[30]中的简支空心板、简支T梁、连续T梁、连续小箱梁作为中小跨混凝土梁桥的代表，简支空心板的跨径分别取10、13、16、20 m，简支T梁的跨径分别取20、25、30、35、40 m，连续T梁和连续小箱梁的跨径组合均取5×20 m、5×25 m、5×30 m、5×35 m、4×40 m。另外选取了3座连续箱梁桥作为大跨径混凝土梁桥的代表，桥梁概况见表2。采用MIDAS /Civil建立桥梁的有限元模型进行作用效应的计算，部分桥梁模型如图9(a)所示，采用单梁模型建模，其中空心板、T梁和小箱梁横向分别由10片、5片和4片主梁组成，以中梁为计算对象。

表2 大跨连续箱梁桥概况Table 2 General Informations of Long Span Continuous Box Girder Bridges

对于横向由多片主梁组成的桥梁结构，边梁和中梁的尺寸存在差异且横梁会产生温度变形，因此计算温度效应时需要评估空间效应的影响。为分析考虑空间效应与否对竖向温度梯度效应计算结果的影响，选取20 m跨径的简支空心板(横向10片主梁)和4×40 m跨径的连续小箱梁(横向4片主梁)建立的空间梁格模型如图9(b)所示，调整虚拟横梁的刚度使中梁在最不利车道荷载作用下按梁格模型计算的挠度与按实用空间理论简化为单梁模型计算的挠度一致。在单梁和梁格模型中施加图10所示的2种温度梯度，提取中梁的挠度和截面上缘应力，如图11所示，可以看到2种模型的计算结果相近，除在连续小箱梁挠度较小的中间两跨单梁模型的相对误差较大外，其余温度效应单梁模型的相对误差在7%以内。因此，本文将忽略空间效应的影响，采用单梁模型计算温度效应。

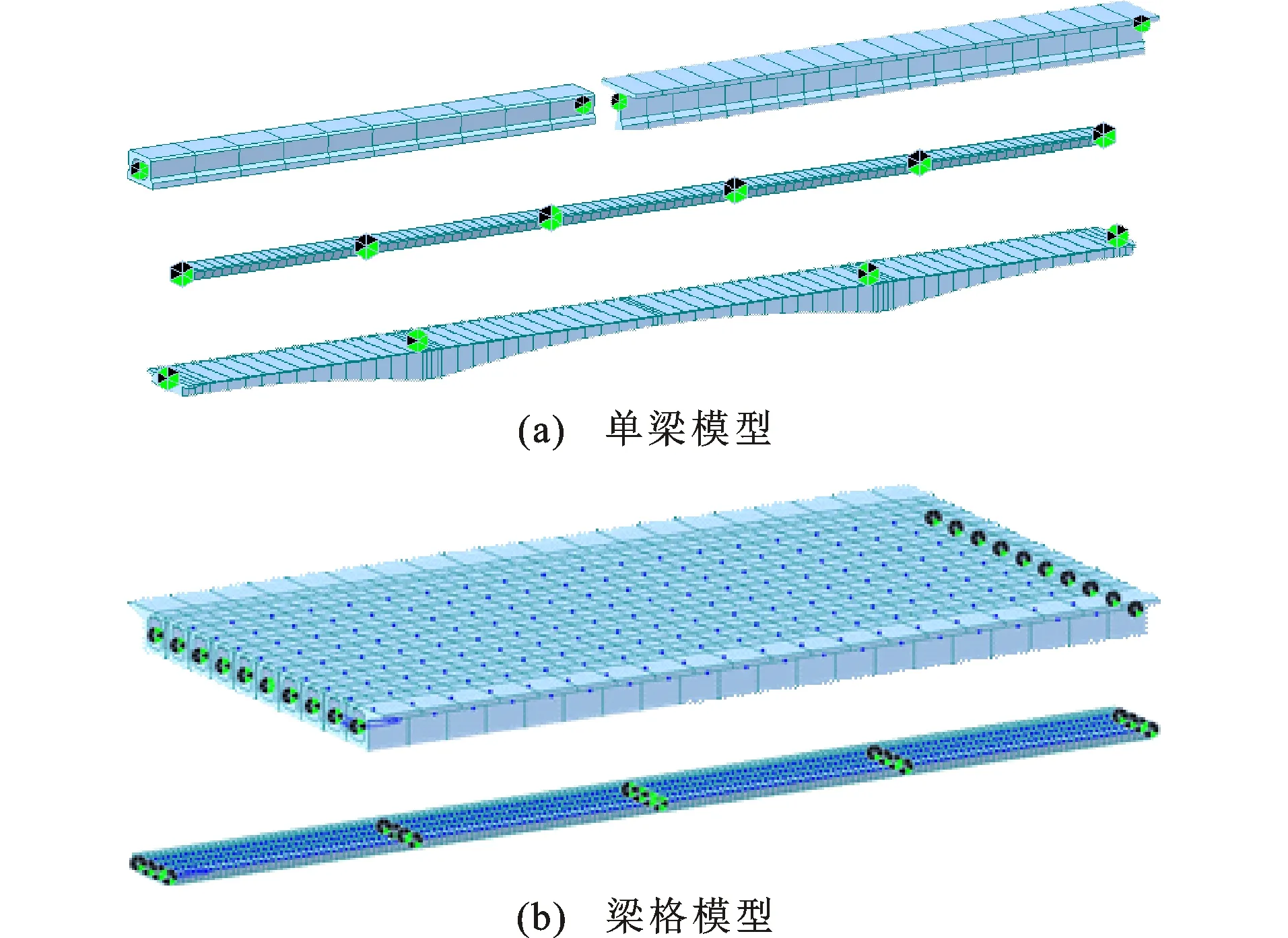
图9 桥梁计算模型Fig.9 Calculation Models of Bridges

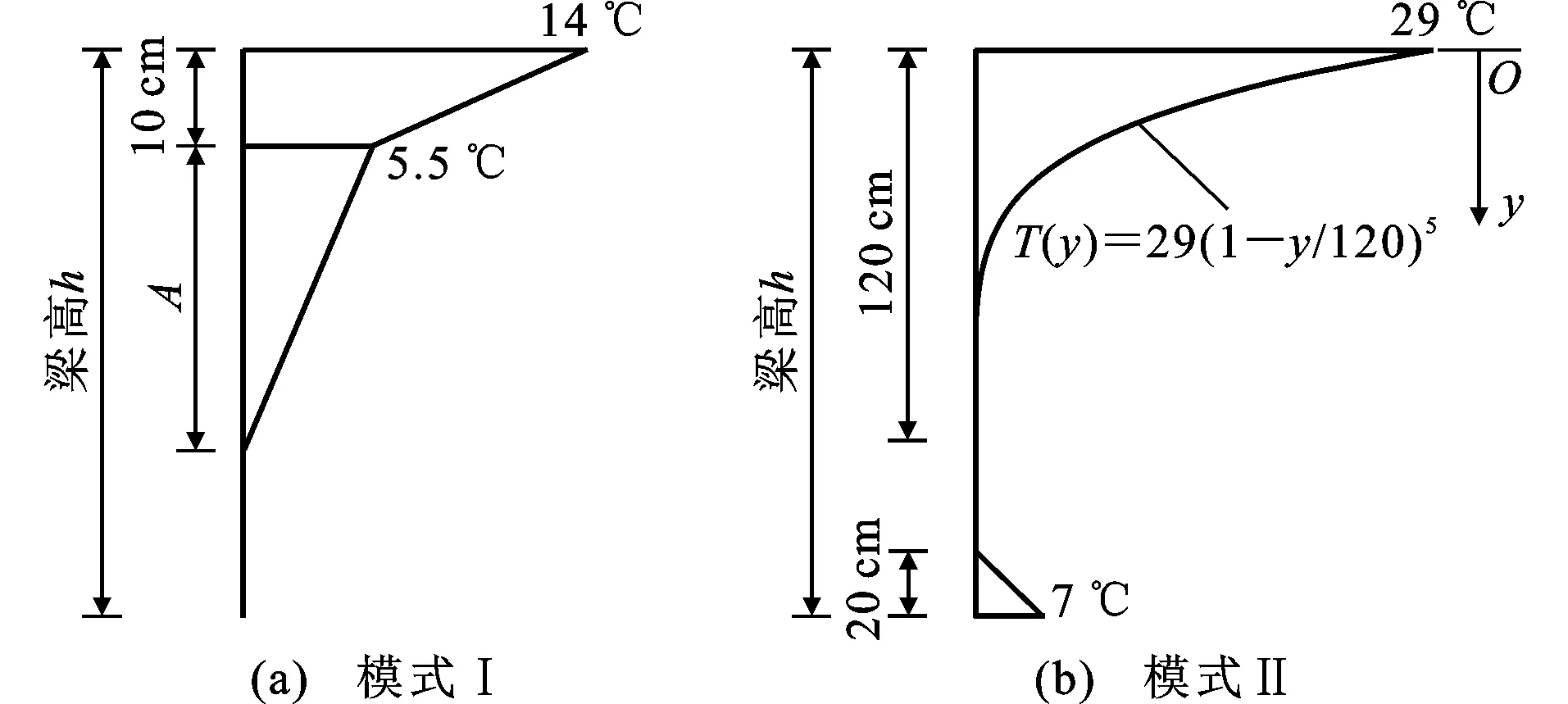
图10 竖向温度梯度Fig.10 Vertical Temperature Gradients

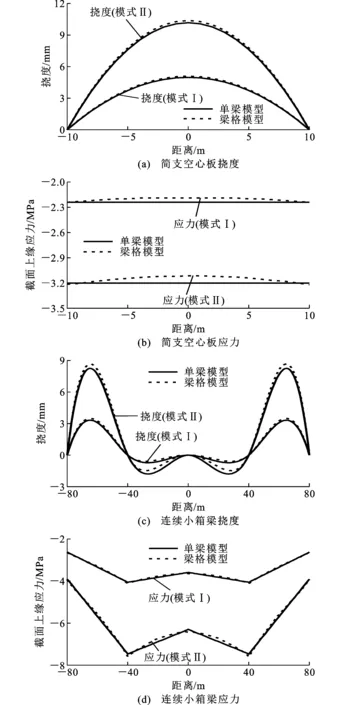
图11 不同模型计算温度效应对比Fig.11 Comparison of Temperature Effects Calculated by Different Models

2.1.2 作用及效应比例系数

结构自重包含了梁体自重以及现浇层、桥面铺装和防护矮墙等二期恒载，主梁混凝土重度取26 kN·m-3，现浇层混凝土重度取25 kN·m-3，沥青铺装重度取24 kN·m-3，一侧护栏自重集度取9.1 kN·m-1，二期恒载在横向均摊到每片主梁上。汽车荷载取公路Ⅰ级车道荷载，以最不利方式加载，荷载横向分布系数按铰接板法或刚接梁法计算，选取的桥宽均为两车道布置，横向车道布载系数为1.00，纵向折减系数由桥梁计算跨径按《公路桥涵设计通用规范》表4.3.1-6取值[12]。温度作用按2种模式施加：模式Ⅰ为中国公路规范JTG D60—2015[12]中的竖向正温度梯度，温度基数T1、T2按10 cm厚沥青混凝土铺装层取值，分别为14 ℃和5.5 ℃，如图10(a)所示；模式Ⅱ为文献[9]中的“5次抛物线+底部直线”的竖向正温度梯度，温度基数T1、T2按分区Ⅳ取值，分别为29 ℃和7 ℃，如图10(b)所示。根据第1节的分析，模式Ⅰ和模式Ⅱ分别为各类温度梯度下计算温度效应的下限和上限。

对于混凝土梁桥而言，自重、汽车和温度是3种主要的作用形式，引起的效应决定了截面尺寸、钢筋布置等设计参数以及抗裂验算和挠度验算等内容。为论证温度效应在上述设计、验算内容中的意义和重要性，本文计算了式(1)所示的3类效应的比例系数进行比较分析。在桥梁不同的验算位置，3种效应可能存在抵消作用导致总效应很小、计算的比例系数过大，因此本文采取对分效应的绝对值求和计算比例系数。式(1)比例系数的正、负号区分了挠度的方向和拉、压应力，比例系数的数值表明了作用效应所占的比重。

(1)

式中：ηG、ηQ、ηT分别为自重、汽车、温度效应的比例系数；SG、SQ、ST分别为自重、汽车、温度效应标准值。

混凝土梁桥健康监测系统记录的效应变化主要源于汽车和温度作用以及可能的结构损伤，为分析温度效应在其中可能占到的比重，本文计算了式(2)所示的温度效应比例系数γT。分析汽车和温度效应的相对比例，明确控制性的可变作用，也可为桥梁设计提供参考。

(2)

2.2 中小跨混凝土梁桥

2.2.1 简支梁桥

对简支梁桥的跨中位移和跨中截面应力进行分析，计算不同作用效应的比例系数。

温度作用引起简支空心板和简支T梁的跨中上拱位移变化范围分别为2.38～10.16 mm和3.30～16.86 mm，图12给出了跨中位移比例。从图12可知，随着跨径增大，自重位移占比ηG增加，汽车和温度位移占比ηQ、ηT减小，温度位移比例γT基本保持不变。在温度梯度模式Ⅰ和模式Ⅱ作用下，空心板ηT=12.52%～20.47%、22.63%～28.08%，γT=30.86%、44.44%；T梁ηT=10.13%～15.87%、22.54%～31.79%，γT=33.64%、56.05%。温度位移接近甚至超过汽车位移，跨径较小时与自重位移相近。相同的跨径，T梁的温度位移占比要略高于空心板。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁ηT比空心板高3.35%、9.16%，T梁γT比空心板高4.55%、9.96%。

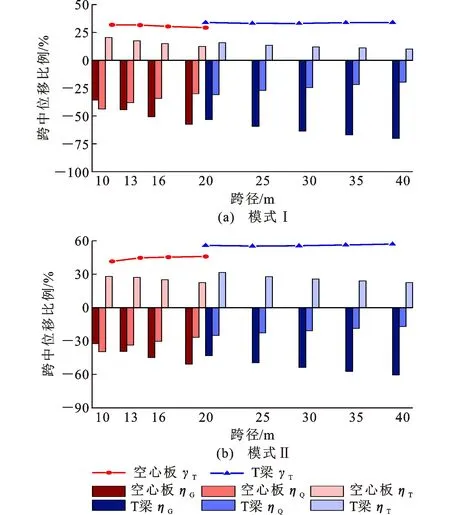
图12 跨中位移比例Fig.12 Proportions of Midspan Deflections

温度作用引起简支空心板和简支T梁的跨中截面上缘自压应力在-1.58～-3.20 MPa和-2.30～-4.06 MPa之间，图13给出了应力比例。从图13可知，随着跨径增大，自重应力占比ηG增加，汽车应力占比ηQ减小。在温度梯度模式Ⅰ和模式Ⅱ作用下，空心板ηT=-13.28%、-18.50%，γT=-20.44%～-28.62%、-28.57%～-36.42%，温度应力在跨径较小时与自重应力接近，跨径增大时逐渐接近汽车应力；T梁ηT=-17.93%～-24.67%、-24.94%～-30.76%，γT=-44.73%～-47.49%、-52.34%～-57.90%，温度应力与汽车应力相当，跨径较小时与自重应力接近。相同的跨径，T梁的温度应力占比要高于空心板。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁的ηT比空心板高-11.44%、-12.88%，T梁的γT比空心板高-16.11%、-15.92%。

图13 跨中截面上缘应力比例Fig.13 Proportions of Stresses on Top Edge at Midspan Section

温度作用引起简支空心板和简支T梁的跨中截面下缘自压应力分别在-0.67～-2.35 MPa和-0.65～-3.96 MPa之间，图14给出了应力比例。从图14可知，随着跨径增大，自重应力占比ηG增加，汽车和温度应力占比ηQ、ηT减小。在温度梯度模式Ⅰ和模式Ⅱ作用下，空心板ηT=-4.59%～-6.80%、-14.44%～-18.38%，γT=-11.14%、-29.35%；T梁ηT=-3.52%～-5.55%、-17.20%～-20.74%，γT=-12.70%、-39.26%～-46.23%。考虑底部升温段时，温度应力接近于汽车应力。相同的跨径，T梁的温度应力占比要略高于空心板。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁的ηT比空心板高-0.96%、-6.30%，T梁的γT比空心板高-1.45%、-8.51%。

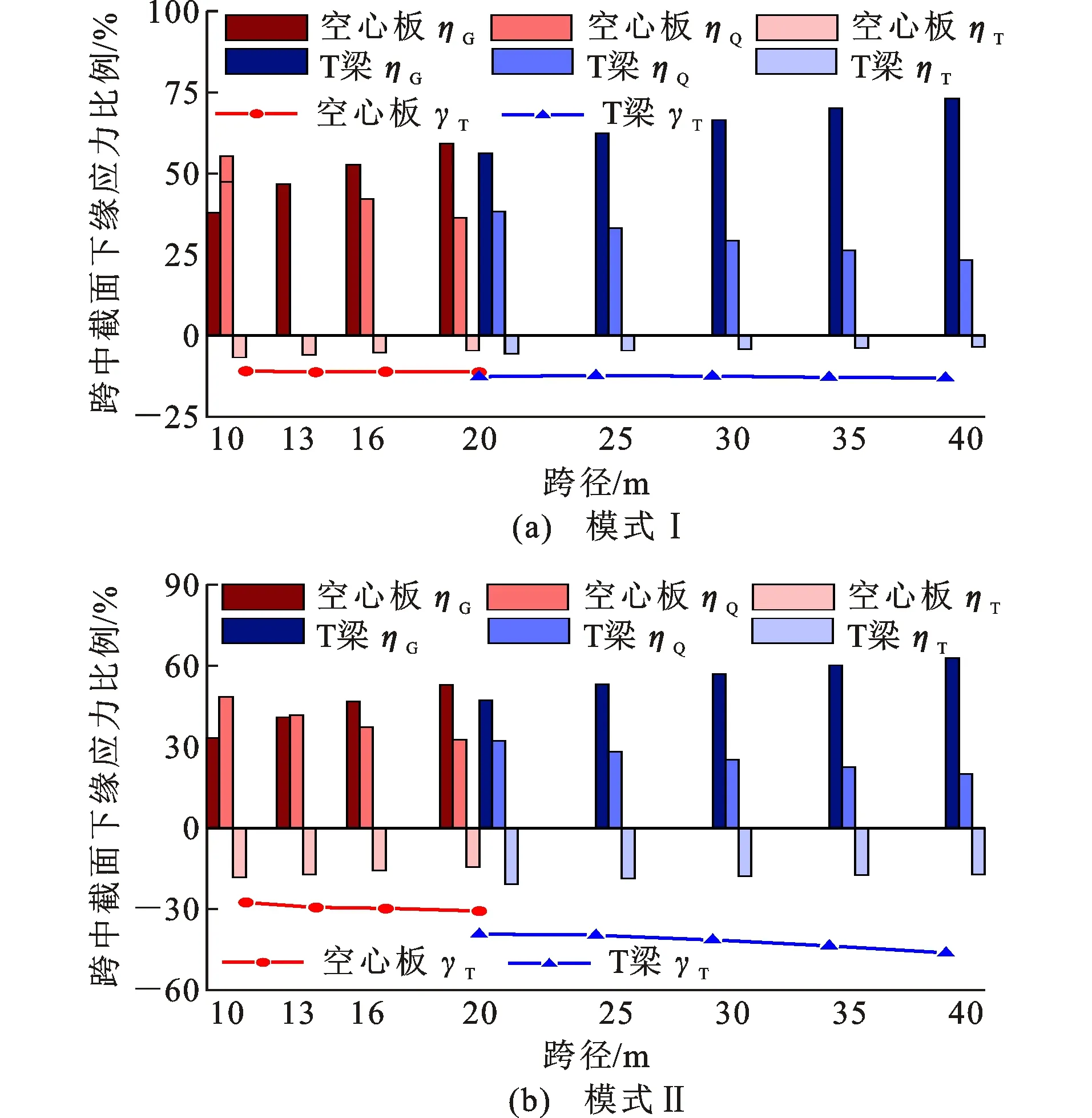
图14 跨中截面下缘应力比例Fig.14 Proportions of Stresses on Bottom Edge at Midspan Section

2.2.2 连续梁桥

对连续梁桥的边跨跨中位移、次边跨跨中截面应力和边跨-次边跨墩顶截面应力进行分析，其中次边跨跨中截面代表正弯矩区，边跨-次边跨墩顶截面代表负弯矩区。自重效应计算时考虑了结构先简支后连续的施工方法，梁体自重效应按简支梁计算，二期恒载效应按连续梁计算。

温度作用引起连续T梁和连续小箱梁的边跨跨中上拱位移在1.25～6.63 mm和1.52～8.26 mm之间，图15给出了位移比例。从图15可知：随着跨径增大，自重位移占比ηG增加，汽车和温度位移占比ηQ、ηT减小，温度位移比例γT基本保持不变。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁ηT=5.09%～8.42%、12.59%～19.48%，γT=20.97%、41.30%；小箱梁ηT=3.91%～7.52%、9.80%～17.05%，γT=17.25%、34.97%。温度位移远小于自重位移，但仍能与汽车位移接近。相同的跨径，T梁的温度位移占比要略高于小箱梁。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁的ηT比小箱梁高0.90%～1.18%、2.13%～2.79%，T梁的γT比小箱梁高2.73%～5.47%、5.10%～8.51%。

图15 边跨跨中位移比例Fig.15 Proportions of Midspan Deflections at Side Span

温度作用引起连续T梁和连续小箱梁的次边跨跨中截面上缘压应力在-3.45～-7.11 MPa和-3.57～-6.88 MPa之间，图16给出了应力比例。从图16可知，随着跨径增大，自重应力占比ηG增加，汽车和温度应力占比ηQ、ηT减小，温度应力比例γT基本保持不变。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁ηT=-30.90%～-42.23%、-45.17%～-55.81%，γT=-65.71%、-77.35%；小箱梁ηT=-25.52%～-36.43%、-38.16%～-49.36%，γT=-58.68%、-71.37%。自应力与次应力叠加产生了较大的温度应力，远超汽车应力，接近或超过自重应力，跨径较小时甚至超过两者总和。相同的跨径，T梁的温度应力占比要高于小箱梁。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁的ηT比小箱梁高-5.12%～-6.36%、-5.88%～-7.70%，T梁的γT比小箱梁高-6.39%～-7.88%、-5.50%～-6.61%。

图16 次边跨跨中截面上缘应力比例Fig.16 Proportions of Stresses on Top Edge at Midspan Section of Secondary Side Span

温度作用引起连续T梁和连续小箱梁截面下缘产生自压应力和次拉应力，叠加后次边跨跨中截面下缘拉应力在1.00～2.50 MPa和1.22～2.34 MPa之间，图17给出了应力比例。从图17可知，随着跨径增大，自重应力占比ηG增加，汽车和温度应力占比ηQ、ηT减小。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁ηT=8.31%～14.08%、7.13%～19.14%，γT=29.00%、26.26%～36.66%；小箱梁ηT=6.23%～12.52%、6.28%～17.22%，γT=23.93%、22.39%～32.93%。自应力和次应力抵消导致温度应力较小，远小于自重应力，跨径较小时能接近于汽车应力。相同的跨径，T梁的温度应力占比要高于小箱梁。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁的ηT比小箱梁高1.56%～2.08%、0.85%～2.01%，T梁的γT比小箱梁高3.35%～7.34%、3.73%～5.61%。

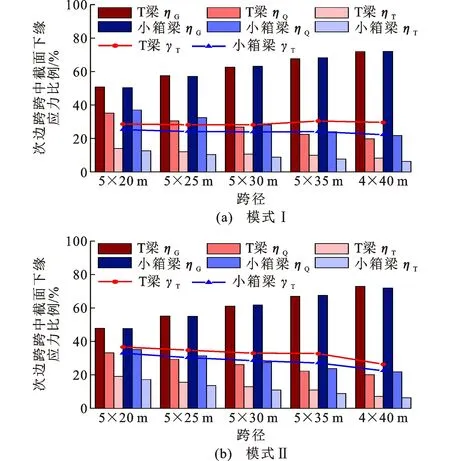
图17 次边跨跨中截面下缘应力比例Fig.7 Proportions of Stresses on Bottom Edge at Midspan Section of Secondary Side Span

温度作用引起连续T梁和连续小箱梁的边跨-次边跨墩顶截面上缘压应力在-3.61～-7.71 MPa和-3.75～-7.47 MPa之间，图18给出了应力比例。从图18可知，随着跨径增大，自重应力占比ηG增加，汽车和温度应力占比ηQ、ηT减小，温度应力比例γT基本保持不变。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁ηT=-48.52%～-55.02%、-63.98%～-68.27%，γT=-70.50%、-81.29%；小箱梁ηT=-43.75%～-51.54%、-58.86%～-64.83%，γT=-63.82%、-75.95%。考虑简支变连续的施工方法，二期恒载引起的自重应力较小，所以温度应力占比较大，接近甚至超过了自重和汽车应力的总和。相同的跨径，T梁的温度应力占比要高于小箱梁。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁的ηT比小箱梁高-2.81%～-4.77%、-2.83%～-5.12%，T梁的γT比小箱梁高-6.10%～-7.55%、-4.90%～-6.04%。

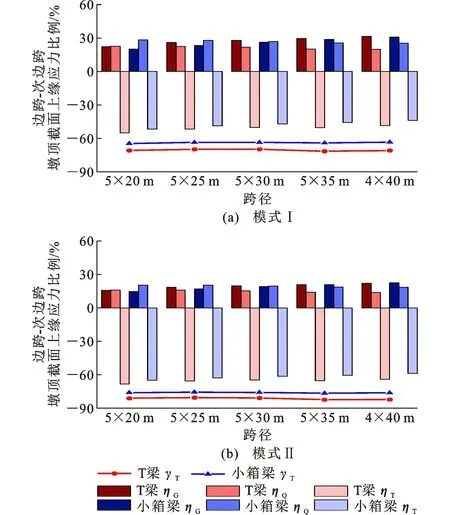
图18 边跨-次边跨墩顶截面上缘应力比例Fig.18 Proportions of Stresses on Top Edge at Pier-top Section Between Side Span and Secondary Side Span

温度作用引起连续T梁和连续小箱梁截面下缘产生自压应力和次拉应力，叠加后边跨-次边跨墩顶截面下缘拉应力在1.53～3.38 MPa和1.60～3.12 MPa之间，图19给出了应力比例。从图19可知，随着跨径增大，自重应力占比ηG增加，汽车和温度应力占比ηQ、ηT减小。在温度梯度模式Ⅰ和模式Ⅱ作用下，T梁ηT=18.93%～24.05%、22.48%～33.87%，γT=37.30%、42.87%～50.30%；小箱梁ηT=15.70%～23.36%、20.32%～32.89%，γT=31.40%、36.15%～45.71%。虽然自应力与次应力存在抵消，但是由于二期恒载应力较小，所以温度应力仍能与自重和汽车应力相当。相同的跨径，T梁的温度应力占比要高于小箱梁。在温度梯度模式Ⅰ和模式Ⅱ的作用下，T梁的ηT要比小箱梁高0.69%～3.23%、0.98%～2.45%，T梁的γT比小箱梁高4.13%～8.41%、4.59%～6.98%。

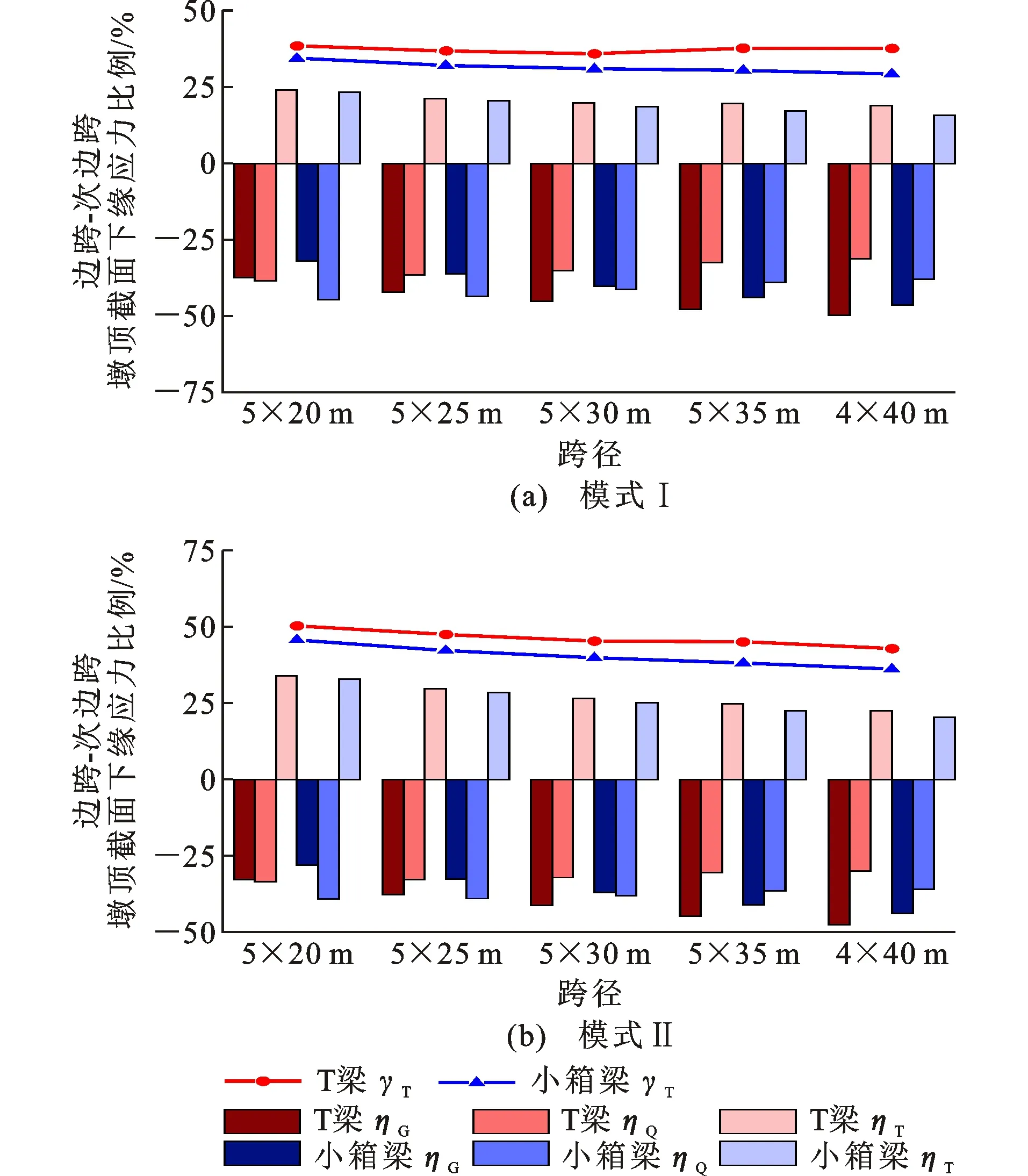
图19 边跨-次边跨墩顶截面下缘应力比例Fig.19 Proportions of Stresses on Bottom Edge at Pier-top Section Between Side Span and Secondary Side Span

2.3 大跨混凝土梁桥

对大跨连续梁桥中跨跨中位移、截面应力和边跨-中跨墩顶截面应力进行分析，其中中跨跨中截面代表正弯矩区，边跨-中跨墩顶截面代表负弯矩区。

温度作用引起大跨连续梁桥中跨下挠可达-26.82 mm，引起的截面上缘压应力可达-9.52 MPa，引起的截面下缘拉应力可达2.68 MPa，图20给出了各项效应的比例。从图20可知，大跨连续梁梁高增大导致自重效应占比ηG极大，绝大部分在60%以上，有的甚至超过90%，且随跨径增大仍有提高的趋势。温度作用在截面上缘产生的自应力和次应力叠加，导致温度应力远超过汽车应力。在温度梯度模式Ⅰ和模式Ⅱ作用下，跨中截面上缘ηT=-24.74%～-30.17%、-38.98%～-45.70%，γT=-65.02%～-73.93%、-78.36%～-84.64%；墩顶截面上缘ηT=-23.82%～-29.02%、-37.21%～-42.91%，γT=-76.92%～-81.71%、-85.97%～-89.44%。温度作用在跨中产生的位移和在截面下缘产生的应力占比较小，但仍能与汽车效应相当。在温度梯度模式Ⅰ和模式Ⅱ作用下，跨中位移ηT=-3.65%～-7.47%、-9.76%～-17.88%，γT=-25.45%～-28.86%、-47.92%～-52.69%；跨中截面下缘应力ηT=6.28%～10.67%、8.73%～15.76%，γT=33.86%～39.39%、44.52%～48.18%；墩顶截面下缘应力ηT=0.4%～1.69%、-12.41%～-18.15%，γT=5.42%～12.3%、-57.40%～-72.26%。

图20 大跨箱梁桥的效应比例Fig.20 Proportions of Effects in Long Span Box Girder Bridges

3 结语

(1)不同国家和行业规范中混凝土梁桥的温度梯度模式在梯度曲线形式和温度基数取值方面存在较大差异。温度梯度曲线中顶部温差的影响深度越大，桥梁的变形和次生弯矩越大，底部升温段使截面下缘产生更大的自压应力。不同的铺装层类型和气候条件下，桥梁温度基数存在差异，进而导致温度效应相差可能达到1.5倍～2.0倍。温度梯度曲线形式和温度基数取值对效应计算结果具有同等程度的影响，后续研究应结合桥梁温度场的实测或数值模拟结果分析各温度梯度模式的适用性。

(2)结构体系和截面形式相同的中小跨混凝土梁桥随着桥梁跨径的增大，自重效应占比增加，汽车和温度效应占比减小，而温度和汽车效应的相对比例基本保持不变；相同的结构体系和跨径，T梁的温度效应占比要高于空心板和小箱梁，高出0.6%～16.5%不等。

(3)对于中小跨简支梁桥，温度作用引起的桥梁变形和截面上缘应力在桥梁跨径较小时与自重效应接近，在桥梁跨径较大时与汽车效应相近，甚至超过汽车效应；当温度梯度中考虑底部升温段时，温度作用引起的截面下缘应力与汽车效应相近。

(4)对于中小跨连续梁桥，温度作用引起的截面上缘应力超过自重和汽车效应，甚至超过两者的总和；墩顶截面下缘应力与自重和汽车效应相当；桥梁变形和跨中截面下缘应力虽然远小于自重效应，但仍与汽车效应相近。

(5)对于大跨径连续箱梁桥，自重效应占比非常大，能达到90%以上。温度作用引起的截面上缘应力要远超汽车效应，能达到其5倍以上，且随桥梁跨径增大仍有提高的趋势；温度作用引起的桥梁变形和截面下缘应力与汽车效应相当。