考虑风速风向联合分布的双坡屋面风致疲劳研究

李寿英，曹镜韬，李寿科

(1. 湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙 410082；2. 湖南科技大学土木工程学院，湖南湘潭 411201)

0 引 言

金属屋面板造型美观、制作方便，广泛应用于各种工业、商业、民用建筑。近年来，中国沿海地区频频出现大跨度屋面风毁案例[1]，屋面系统作为围护结构，对风荷载尤其敏感，且表现出极大的不确定性。

疲劳效应往往在风致破坏中起主导作用，金属屋面疲劳损伤的累积会降低其本身的抗风承载力，加速破坏进程[1]。国际现行的金属屋面抗风揭性能检测标准较多，金属屋面静力性能的研究方法相对成熟，但针对屋面板的动态检测标准能否反映真实风荷载的作用仍存在质疑[2-4]，存在多数通过了动态性能检测的屋面板仍发生破坏的现象。Xu[5]从构件层面出发，利用跨中加载法完成了自攻螺钉固定的双跨金属屋面板的静力性能和疲劳性能研究，得到了金属屋面板的静力承载力和疲劳寿命曲线。在此基础上，Kumar等[6-7]提出了考虑长期风环境影响的金属屋面风致疲劳的基本计算流程，以位于平板屋面屋角位置的屋面板为例，在不考虑风向变化时，结合风速统计信息计算了作用在该区域的荷载循环矩阵，利用试验得到的屋面板疲劳寿命曲线估计疲劳损伤。Jancauskas等[8]以台风Winifred的基本参数为计算依据，结合平板屋面的风洞测压试验，计算了一次强台风过境期间屋面板屋角区域的风致疲劳损伤累积值，总结了金属屋面风致疲劳损伤在台风过境期间的累积规律。Xu[9-10]结合TTU模型角部分离区测点的测压结果比较了良态风、台风主控地区建筑结构在设计使用期内的疲劳损伤，基于计算结果评估了澳大利亚TR440低-高-低测试加载序列。已有研究在计算风致疲劳时均忽略了风向的变化，仅考虑最不利风向对屋面进行单点评估，存在一定的局限性。中国学者多数致力于屋面板的静力抗风承载力研究，用于指导实际工程建设，针对屋面板疲劳性能的研究较少[11-14]。

中国多数动态抗风揭检测方法直接参考国外相关标准，如《采光顶与金属屋面技术规程》参考美国UL 580标准。中国气候条件和金属屋面板样式和国外有较大差异，直接借鉴国外标准有很大的不确定性。合理评估屋面系统的疲劳损伤对制定屋面系统动态性能检测标准具有重要意义。为研究长期风荷载作用下大跨度低矮建筑金属屋面板的疲劳损伤分布规律，本文以位于厦门地区的双坡屋面为例，考虑风向变化，基于风洞试验测压结果和风速风向的实测信息，通过简化循环荷载矩阵计算，提出考虑连续变化风速和离散风向角的风致疲劳计算公式，进行良态风环境下双坡屋面50年内的风致疲劳损伤整体评估。

1 疲劳分析方法

1.1 计算方法

目前，计算随机荷载疲劳损伤的方法分为时域和频域2类计算方法。频域方法简单快捷，但是计算精度低于时域方法。时域计算主要包括循环计数和疲劳损伤线性累积计算2个部分。循环计数法中，雨流计数法可较真实地反映随机加载的全过程，因计算精度高被广泛应用。MATLAB平台提供的RainFlow函数参考美国ASTM E1049-85标准提供的雨流计数流程编写。雨流计数法得到的统计结果可通过式(1)计算随机荷载引起的疲劳损伤DF，并可利用Goodman方程考虑荷载均值的影响[5]。

(1)

式中：N为荷载循环总次数；ni为荷载幅值为Si时的荷载循环次数；Ni为荷载幅值为Si时材料或结构的疲劳寿命。

1.2 金属屋面板的选取

金属屋面板疲劳破坏形式与屋面板样式、加固措施、施工质量等因素有关。目前中国对于金属屋面板疲劳性能研究相对较少，相关检测规范多数参考国外已有检测标准。考虑到图1(a)所示的澳大利亚常用的金属屋面板在外形、尺寸、固定方式上与中国常用的自攻螺钉固定金属屋面板相似，本文基于文献[5]的试验结果进行屋面板疲劳分析。Xu[5]以双跨屋面板为研究对象进行疲劳试验，得到了屋面板的疲劳寿命曲线，且根据自攻螺钉固定金属屋面板的受力特点，Xu[5]和Kumar等[6-7]提出可直接应用屋面板的疲劳寿命曲线进行风致疲劳分析。屋面板单板宽760 mm，厚0.43 mm，波峰高度29 mm，跨长1.0 m。该金属屋面板的静力承载极限强度S为7.6 kPa，疲劳性能曲线如图1(b)所示。该金属屋面板的疲劳破坏形式主要表现为自攻螺钉固定位置屋面板的撕裂破坏或螺钉的拔出破坏[5]。

图1 澳大利亚梯形截面金属屋面板Fig.1 Australia Trapezoidal Section Metal Roof Panel

2 极值风速风向联合分布

2.1 数据来源和分析

本文选取厦门市1975年1月1日～2019年12月30日期间记录的日最大风速和相应风向作为样本数据，数据来源于中国气象数据网，总计16 437组，样本数据统计到的最大日极值风速(每日最大10 min平均风速)为36.4 m·s-1。由于数据基数较大，高风速比例较小，风速统计结果仅反映良态风出现的概率。图2(a)和图2(b)分别为由实测数据得到的风速频率分布直方图和风向玫瑰图，图2(c)为实测风速风向联合概率密度，可以看出：日最大平均风速主要集中在3～15 m·s-1，风向以东南风为主，统计结果与实际情况相符。

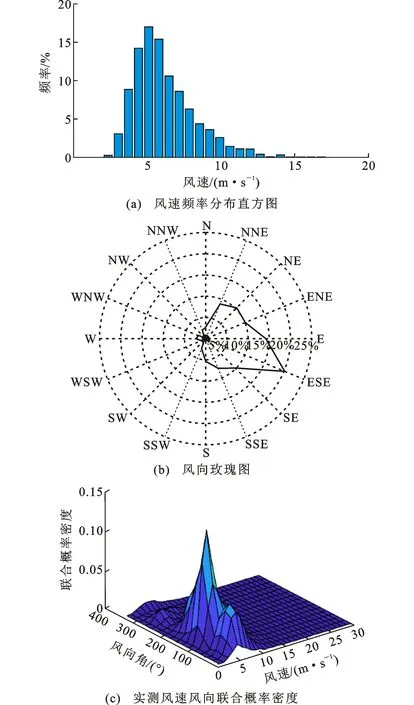
图2 厦门市实测风速风向信息Fig.2 Measured Wind Speed and Direction Information in Xiamen

2.2 极值风速分布

极值风速分布的估计主要包括选取风速样本、建立分布模型、参数估计3个方面，其中常用的极值分布模型有Gumbel分布、Frechet分布、Weibull分布、对数正态分布等，通常采用最小二乘算法、极大似然估计进行参数估计。计算建筑结构风致疲劳损伤的理想统计数据是10 min平均风速和对应风向，但对于风振疲劳寿命期为几十年的建筑结构，王钦华等[15]提出采用月极值风速作为统计样本计算风致疲劳损伤是合理的。考虑到数据来源，采用月极值风速会高估强风天气的出现概率，因此选择日极值风速作为样本数据。

采用Gumbel、Lognormal、Weibull三种分布模型拟合厦门地区日极值风速，采用最小二乘算法估计分布参数，拟合结果如图3所示，其中R2为判定系数。由图3可知：对全风向日极值风速而言，Gumbel和Lognormal分布拟合精度较高，Gumbel分布略优于Lognormal分布，Weibull分布的尾部长度属于有限有界型，这与风速有限无界特性的特点不符[16]。因此，选取Gumbel分布作为厦门市日极值风速的概率模型。

图3 风速概率密度函数拟合结果Fig.3 Wind Speed Probability Density Function Fitting Result

2.3 风向分布

中国气象站风向记录采用16方位，风洞测压试验往往间隔5°或10°。为方便利用测压结果和风向统计信息进行风致疲劳计算，采用Johnson等[17]建议的基于离散角变量的连续概率密度结构模型，避免风向角统计的不连续性问题。用于风向拟合的常用角变量分布包括谐波函数、Von Mises分布。

采用谐波函数拟合风向概率密度函数f(θ)[式(2)]形式较为复杂，函数阶次对拟合精度影响较大。采用三角函数族逼近离散数据点的问题存在惟一解，解的形式如式(3)所示。采用4～7阶谐波函数拟合风向概率密度函数的拟合结果如表1所示。

(2)

(3)

式中：α0、βi、γi均为谐波函数的待定参数；n为谐波函数阶次；θk′、f(θk′)分别为已知风向角及其出现的概率；N′为风向区间个数，N′=16；θ为离散风向角。

由表1可以看出：采用4阶谐波函数的拟合精度较低，5阶谐波函数拟合精度达0.951，继续增加谐波函数阶次到第6阶，拟合精度的提高效果并不明显。由于数据点个数有限，谐波函数拟合最高阶次理论上只能达到7阶，7阶谐波函数拟合精度为0.990。

表1 谐波函数参数拟合值Table 1 Fitted Values of Harmonic Function Parameters

Von Mises分布又被称为圆周正态分布，常用于描述方向数据，其概率密度函数f(θ)为

(4)

式中：I0(·)为0阶修正贝塞尔函数；k′为尺度参数,k′≥0；μ为位置参数，0≤μ≤2π。

多数统计结果表明，风向角变量一般具有多峰值，单一的Von Mises分布不能完整描述风向圆周分布特性，通常采用混合Von Mises分布表示风向角变量的分布，即

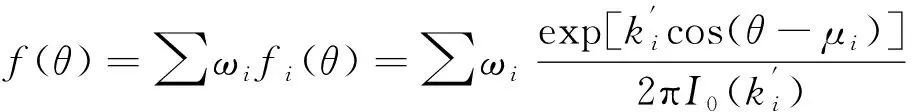
(5)

式中：ωi为组合系数，满足∑ωi=1。

采用最小二乘法进行参数估计，未知参数的初值取值会直接影响参数求解结果和求解效率。采用文献[18]中提到的方法进行参数估计，结果见表2。由表2拟合结果可知：4阶Von Mises分布的拟合精度为0.994，混合Von Mises分布的拟合精度总体高于谐波函数拟合精度。因此，采用4阶混合Von Mises分布描述风向变量。

表2 混合Von Mises分布参数拟合值Table 2 Fitted Values of Von Mises Mixture Model Parameters

2.4 风速风向联合分布

风速风向联合分布属于角度-线性分布，风速、风向并不总是相互独立的，二者之间的相关性通常不能直接忽略[16,19-21]。Copula函数最初广泛应用于统计、金融、风险管理等领域，近几年被引入水文流量分析等工程领域，是处理随机变量相关性的有效方法[22]。因此，本文结合拟合结果，选择合适的Copula函数建立风速风向联合分布模型。

Copula函数可以分别考虑变量的边缘分布和变量间的相关性，Copula函数形式多样，对正负相关性均适用，且求解方便。若计F(x)和G(y)分别为x、y的边缘分布函数，f(x)和g(y)为对应的概率密度函数，则x、y的联合分布函数L(x,y)和联合概率密度函数l(x,y)可表示为

L(x,y)=C[F(x),G(y)]

(6)

(7)

本文采用形式较为简单的4种单参数Archimedean Copula函数构造风速风向联合分布，Copula函数表达式如表3所示。可采用Kendall秩相关系数直接计算单参数Archimedean Copula函数的参数，即

表3 Archimedean Copula函数Table 3 Archimedean Copula Function

(8)

式中：sign(·)为符号函数；M为数据个数；x1i、x2j分别表示序列x1、x2中的第i个、第j个数据，τ为相关系数。

由厦门地区实测数据计算得到相关系数τ=-0.135，表示风速风向呈现弱负相关性。

根据式(9)计算矩形区域u∈[0,30]和θ∈[0°,2π]内共480个离散点的风速风向联合分布概率密度拟合值，和实测值进行比较，通过R2检验4种方法的拟合优度。

f(u,θ)=c[F(u),F(θ)]f(u)f(θ)

(9)

式中：c(·)为Copula函数的密度函数；F(u)、f(u)分别为采用Gumbel分布描述的风速分布函数和概率密度函数；F(θ)、f(θ)分别为采用Von Mises分布描述的风向分布函数和概率密度函数。

图4为采用3种Copula函数拟合的风速风向联合概率密度函数的图像，可以看出三者均可反映厦门市的主要风向，每个风向角下对应的日极值风速具有相同的变化规律。由拟合结果可知，GH、AMH、Frank三种Copula函数拟合结果均较好。虽然通过Kendall秩相关系数计算得到的GH Copula函数的参数α超出了表3中所示的参数范围，但是并未影响拟合精度。Clayton Copula函数的参数α=-0.2376<0，拟合结果较差，仅为50%。由此，本文采用Frank Copula函数描述厦门市的风速风向联合分布，根据建筑实际高度进行修正，即

图4 风速风向联合概率密度函数拟合结果Fig.4 Joint Probability Density Function of Wind Speed and Direction Fitting Result

{-0.003eα[F(u/0.871 6)+F(θ)+1](e-0.003-1)}/

{e-0.003(F[u/0.871 6)+F(θ)+1]+e-0.003-

e0.003[F(u/0.871 6)+1]-e-0.003[F(θ)+1]}2

(10)

由于无法获得Von Mises分布的积分形式，本文采用数值积分计算F(θ)的值。

3 双坡屋面风致疲劳损伤估计

3.1 风洞试验概况

本文选取尺寸为13.7 m×9.1 m×4.0 m、坡度为1/60的双坡屋面作为算例。测压试验在湖南大学HD-2风洞的高速试验段进行，试验模拟地貌为B类。模型几何缩尺比为1∶50，风速比为1∶3，相应的时间比为3∶50。屋盖表面共布置130个测点，每个测点的控制面积约为1.0 m2，详细测点布置和风向角定义见图5，测试风向角间隔5°，共计72个风向角。采样时长约30 s，采样数据点10 000个。通过式(11)计算得到相应的风压系数Cpi(t)。

图5 风洞试验模型Fig.5 Wind Tunnel Test Model

(11)

式中：Pi(t)为风压时程；P0为静压；ρ为空气密度，取值为1.225 kg·m-3；uh为屋盖最高点处的平均风速。

3.2 试验风速下屋面板疲劳损伤估计

风洞测试风速为11 m·s-1，代表实际风速33 m·s-1。图6(a)、(b)分别为135°风向角下屋面平均风压系数等值线图和脉动风压系数等值线图。在135°风向角下，平均风压系数等值线与来流屋面对角线大致呈对称锥形分布，在屋面等值线锥形的中心处其风压系数最大可达-1.5；最大脉动风压系数为0.5，出现在2个锥形涡中心位置。

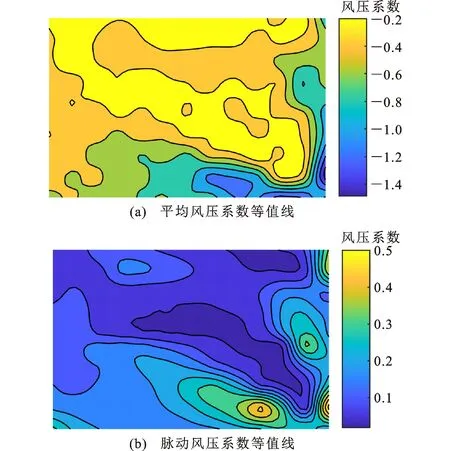
图6 135°风向角下风压系数等值线Fig.6 Contour Map of Wind Pressure Coefficient at 135° Wind Direction

以135°风向角下位于气流分离位置的62号测点测压结果为例，计算屋面板上各点在33 m·s-1的风速下约8 min内的疲劳损伤。通过雨流计数法可得到式(12)所示的循环荷载矩阵N0。

(12)

式中：N0为荷载循环总数；h为循环荷载所占比例；循环荷载均值为0.5ρu2CPmean,i，幅值为0.5ρu2CPrange,j，CPmean,i、CPrange,j分别为采用雨流计数法得到的风压系数均值、风压系数幅值。

62号测点代表区域8 min内荷载循环总数N0=2 968，图7为雨流计数法得到的循环荷载计数结果，可以看出，循环荷载主要集中在幅值较小的区域。基于循环荷载矩阵N0，可直接利用式(1)按照疲劳损伤线性累积理论计算疲劳损伤。

图7 62号测点区域循环荷载Fig.7 Load Cycle in Area of No.62 Measuring Point

图8为疲劳损伤分布等值线。图8(e)为135°风向角下金属屋面的疲劳损伤分布等值线，图8(e)与图6(b)所示的脉动风压系数具有类似的分布规律，位于气流分离屋檐位置处的金属屋面板疲劳损伤最大，屋面板疲劳损伤等值线与来流屋面对角线大致呈锥形分布，2个锥形涡分布并非完全对称。由图7可知，循环荷载的均值水平集中在-0.25ρu2～0，脉动风压对疲劳计算结果起决定性作用。可以发现除来流方向的角部气流分离区域外，大部分屋面区域的疲劳损伤很小，疲劳损伤最大值为0.003 5。

由图8可知：135°风向角下金属屋面的疲劳损伤最大区域为来流屋檐位置(62号测点)，来流屋角位置的疲劳损伤相对较小；当风向角从115°变化到135°时，屋面板易损区域由来流屋角位置逐渐转移到来流屋檐位置，疲劳损伤最大累积值同时由0.006减小到0.003 5；当风向角从135°变化到155°时，屋面板易损区域再次发生变化。因此，风向对屋面板疲劳损伤分布规律的影响不可忽视；屋面板易损区域对风向角较敏感，在考虑长期风环境计算屋面板疲劳损伤时，风向角设置不宜过于离散。

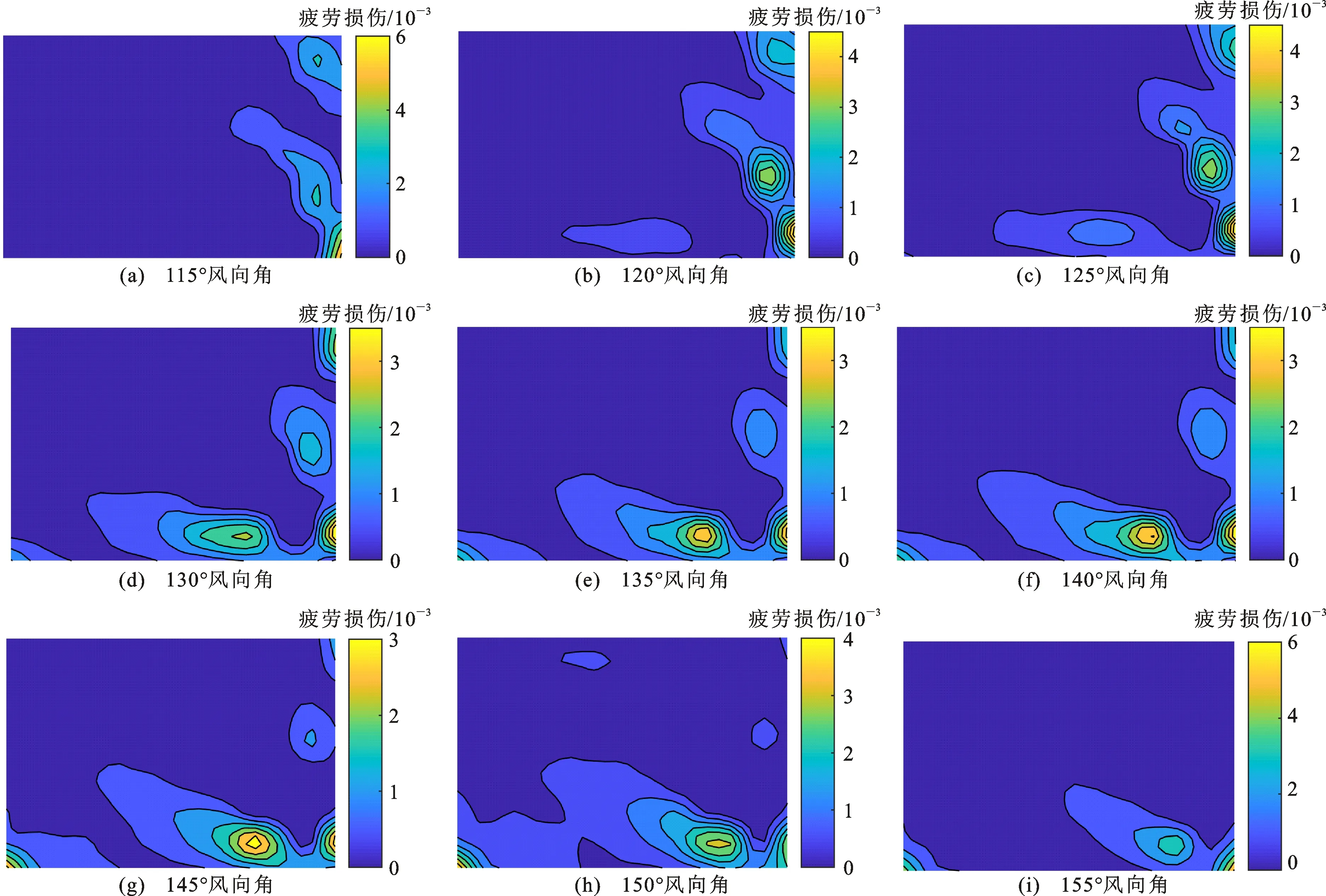
图8 疲劳损伤分布等值线Fig.8 Contour Map of Fatigue Damage Distribution

3.3 考虑风速风向的屋面板疲劳损伤估计

第3.2节得到了金属屋面板在72个风向角下，平均风速为33 m·s-1，持时约8.4 min的疲劳损伤值。文献[7]中给出了屋面板疲劳损伤的计算流程，计算流程如下：

(1)对于给定的平均风速Vi，在设计期T内屋面某测点代表区域荷载循环总次数Nvi为

(13)

(2)给定平均风速Vi对应的循环荷载矩阵Nvi为

Nvi=NviH

(14)

(3)设计期T内的总循环荷载矩阵Ntotal为

(15)

上述过程需计算测点在每个离散风向角和离散风速下的荷载矩阵，最后组成总荷载矩阵，计算过程复杂。对上述过程进行简化，提出考虑连续变化风速和离散风向角的疲劳计算公式。循环荷载总数和平均风速成正比[16]，定义风速比ks=u/u0，若计风速u0下某测点代表区域荷载循环总数为N0，则风速u下的荷载循环总数N=ksN0，循环荷载矩阵N=NH，风速u下对应循环荷载均值为0.5ρu2CPmean,i，幅值为0.5ρu2CPrange,j的荷载循环次数nij=hijksN0。

若考虑风速风向联合分布，将疲劳损伤计算扩展到整个计算时间年限，则需考虑风速变化时屋面板某一区域在同一风向角、相同时间内屋面板疲劳损伤累积变化规律。第3.2节中计算屋面板疲劳损伤时均考虑了循环荷载均值的影响，采用Goodman方程对循环荷载幅值进行修正。考虑到良态风环境下平均风速通常小于33 m·s-1，若不考虑风速变化时对循环荷载幅值修正的影响，则可推导出某测点代表区域在同样时长，特定风向角下，风速u=ksu0时的疲劳损伤值DF(ks)和风速u0时的疲劳损伤值Du0之间的关系，如式(16)所示，疲劳估计结果偏于保守。

(16)

式中：Dij为循环荷载引起的疲劳损伤，对应循环荷载均值为0.5ρu2CPmean,i，幅值为0.5ρu2CPrange,j，循环次数为nij；b为表示屋面板疲劳性能的参数；n′、m′分别为循环荷载矩阵中均值、幅值的划分组数。

由式(16)可知，金属屋面板的风致疲劳损伤随风速增加按照指数型增长，增长速度与屋面板的疲劳性能直接相关。

在时间T内某测点的疲劳损伤值Dtotal可用式(17)计算。

(17)

式中：Dθi为该测点在θi风向角下对应的疲劳损伤；fH(u,θ)为根据建筑实际高度修正得到的概率密度函数。

图9为50年内双坡屋面建筑金属屋面板的疲劳损伤分布。可以看出：除边角等气流分离区域外，屋面板大部分区域疲劳损伤累积值小于0.1。1号、61号、68号测点代表区域均有较大可能发生疲劳破坏。由于厦门地区风向主要集中在东北和东南方向，68号、61号测点代表区域疲劳损伤均大于1号测点区域(西南边角)。68号测点疲劳损伤累积值最大，为0.746，金属屋面板仅在风荷载作用下即有可能发生疲劳破坏[8]。

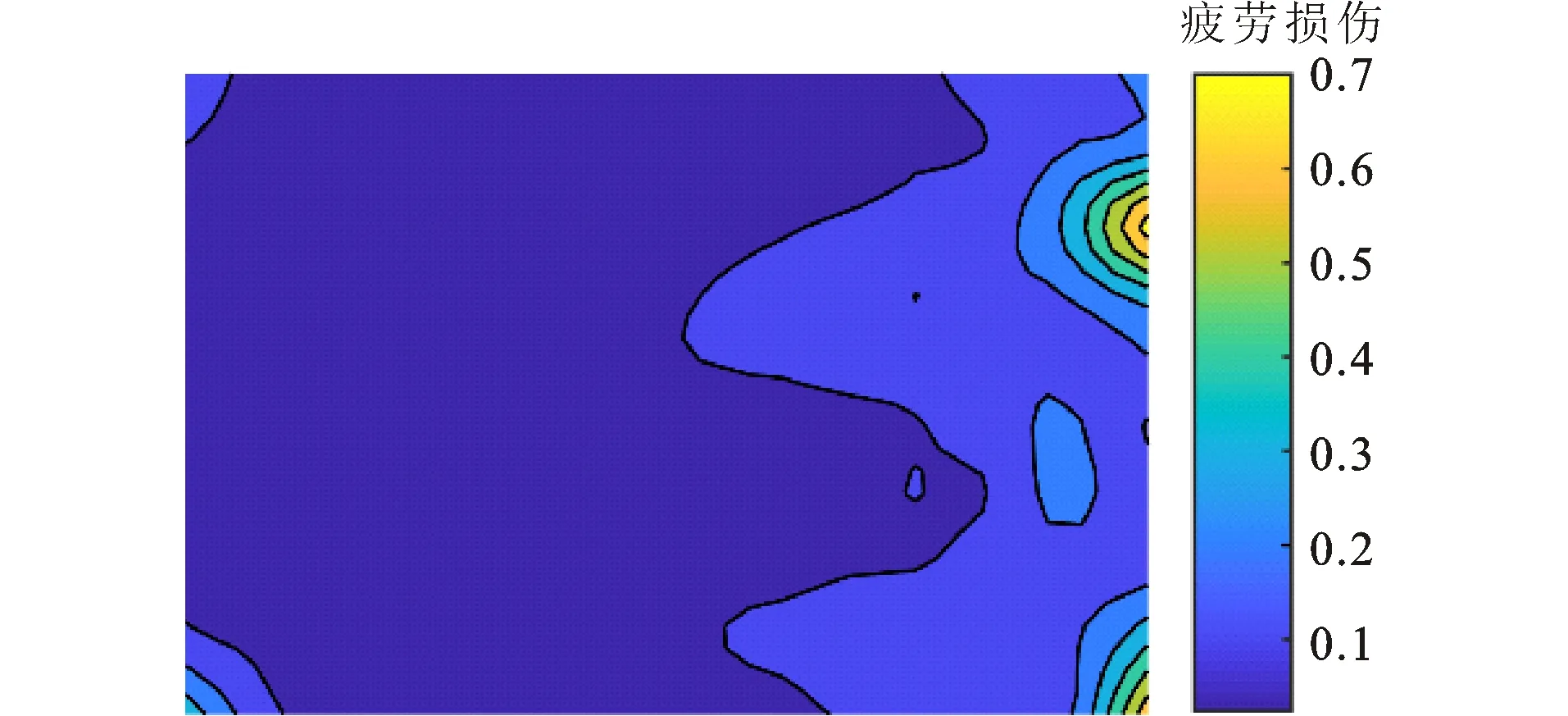
图9 双坡屋面50年风致疲劳损伤分布等值线Fig.9 50-year Wind-induced Fatigue Damage Distribution Contour Map of Double-slope Roof

为方便描述屋面各区域的易损性，并考虑到材料可能在疲劳损伤为0.3～3的区间内破坏[23]，取0.1、0.3作为界限值，将双坡屋面初步划分为3个区域。假设某区域的疲劳损伤小于0.1，则不需要采取加固措施，为安全区域；疲劳损伤在0.1～0.3之间为危险区域，可有选择地采取加固措施；疲劳损伤大于0.3的区域为重点加固区域，必须进行加固。关于各区域临界值的界定需要进一步深入研究。

图10为双坡屋面易损区域的界定。双坡屋面板易损区域的界定应综合考虑主导风向和屋面位置等因素。厦门地区主导风向为东北风和东南风，其中东北风集中在45°风向角，东南风集中在112.5°风向角。45°风向角下屋面板易损区域为来流屋檐位置(68号测点)，而112.5°风向角下屋面易损区域为来流屋角位置(61号测点)，图9中的疲劳损伤等值线同样符合以上分析结果。

图10 双坡屋面易损区域界定Fig.10 Vulnerable Area Definition of Double-slope Roof

4 结语

(1)厦门市日极值风速和风向表现为弱负相关性，可用Gumbel描述日极值风速分布，混合Von Mises分布描述风向角分布，日极值风速、风向的相关性可用GH、AMH、Frank三种单参数Archimedean Copula函数准确描述。

(2)对于双坡屋面，建筑所处地区的主导风向、屋面位置等因素会直接影响金属屋面板疲劳损伤的分布，位于主导风向处的迎风屋檐、边角等气流分离位置疲劳损伤累积值远大于屋面板的其他区域。

(3)良态风环境下，13.7 m×9.1 m×4.0 m的双坡屋面板50年内的疲劳损伤最大值为0.746，风荷载有可能引起金属屋面板发生疲劳破坏,引发风揭事故。考虑到实际情况下屋面板承受多种荷载，会加快疲劳破坏进程，因此应更加关注金属屋面板的疲劳破坏问题。