半漂浮式主梁钢管混凝土拱桥黏滞阻尼器减震设计

彭益华，毛立敏

(1. 广西财经学院管理科学与工程学院，广西南宁 530007; 2. 广西交通设计集团有限公司，广西南宁 530029; 3. 中南大学土木工程学院，湖南长沙 410075)

0 引 言

钢管混凝土拱桥因跨越能力大、施工便利、受力合理而在中国应用广泛，最大跨径已达575 m(广西平南三桥)。为了降低恒载以及单根吊杆断裂引起的主梁坠落风险，钢管混凝土拱桥主梁向轻型化、连续化方向发展[1]，即主梁采用钢格子梁与现浇混凝土板组成的钢-混组合结构。然而这种长度较大的连续主梁结构在温差作用下纵桥向变形较大，为释放这种温度变形，通常只约束主梁横桥向的位移，采用半漂浮体系。研究表明中承式拱桥采用半漂浮体系主梁，可以大幅度减小桥墩的地震响应，但主梁在地震作用下的水平位移响应较大[2]。为改善主梁的地震位移响应，应设置黏滞阻尼器等减震装置[3]。

黏滞阻尼器因性质稳定、对环境温度与激励频率的变化不敏感等优点[4-5]，目前已在斜拉桥[5-9]与悬索桥[10-13]等柔性桥梁减震中广泛应用，结果表明选择适当的设置位置与黏滞阻尼器参数能显著改善柔性桥梁结构地震响应，避免地震作用下构件碰撞而引起的局部损坏。近年来，黏滞阻尼器在一些大跨径拱桥中也逐渐得到应用，如主跨300 m的钢箱拱桥[14]为防止地震作用下的碰撞破坏，在肋间平台与主桥钢箱梁之间设置了黏滞阻尼器。对下承式钢管混凝土拱桥，在桥墩与拱脚间设置黏滞阻尼器能大幅减小在地震作用下的拱肋轴力响应[15]。减震装置全桥对称设置可以有效缓解行波效应的不利影响，使拱肋受力趋于均匀，提高材料利用率[16]。对飞鸟式钢管混凝土拱桥，在主梁与拱肋间设置弹性连接对总体控制结构地震响应不如设置黏滞阻尼器效果好。

然而，到目前为止，对大跨半漂浮体系中承式钢管混凝土拱桥黏滞阻尼器减震设计还有待系统研究，黏滞阻尼器设置位置与参数选取方法值得进一步探讨。本文以高速公路上采用半漂浮体系主梁的某跨径320 m中承式钢管混凝土拱桥为工程背景，基于MIDAS/Civil非线性动力时程分析法研究了半漂浮体系中承式钢管混凝土拱桥黏滞阻尼器减震设计，探讨了黏滞阻尼器参数的选取原则与方法，对比分析了阻尼器设置前后的地震响应，验证了方法的正确性，旨在为半漂浮体系中承式钢管混凝土拱桥黏滞阻尼器减震设计提供参考。

1 工程背景与地震动输入

1.1 工程概况

某计算跨径320 m中承式钢管混凝土拱桥的拱肋与基础固接，拱肋矢跨比为1/4，拱肋为变截面桁式钢管混凝土结构，拱肋宽3 m，拱顶截面径向高7 m，拱脚截面径向高12 m，桥面以下拱肋内横向采用缀板连接成横哑铃形，缀板内人工灌注C55补偿收缩混凝土，桥面以上拱肋内横向采用缀管连接。主梁采用钢格子梁与现浇混凝土板组成的连续钢-混组合结构，吊杆横桥向间距23.9 m，顺桥向间距13.4 m。拱上立柱上均为双向活动支座，主引桥交界墩上只有中间支座为顺桥向单向活动支座，其余均为双向活动支座，全桥无固定支座，主梁为纵桥向半漂浮体系。

1.2 有限元计算模型

采用有限元软件MIDAS/Civil建立桥梁空间有限元计算模型，如图1所示，用梁单元模拟拱肋与横撑，基于软件自带的施工阶段联合截面功能来模拟施工过程中钢管混凝土拱肋联合刚度与初应力，采用等效主梁模拟钢-混组合主梁，用只受拉桁架单元模拟吊杆，通过质量单元施加二期恒载，按实际刚度模拟支座，结构阻尼比取为0.05[16]，采用瑞利阻尼。

图1 桥梁有限元计算模型Fig.1 Finite Element Calculation Model of Bridge

1.3 地震动输入

安装了黏滞阻尼器的桥梁结构减震计算通常采用非线性动力时程分析法，这种方法以实际地震记录或人工合成地震波时程作为输入条件，在时域上求解地震响应，得到内力、位移等在时域上的时间历程。根据《公路桥梁抗震设计规范》(JTG/T 2231-01—2020)，该桥为单跨跨径大于150 m的特大桥，属于抗震A类桥梁，桥址处工程场地类别为Ⅱ类，抗震设防烈度为7度，设计基本地震动峰值加速度为0.1g(g为重力加速度)，地震动反应谱特征周期为0.35 s。由工程场地地震安全性评价报告提供的E2地震3条地震波加速度时程如图2所示，峰值加速度为1.7 m·s-2。对地震波进行反应谱分析可得到其对应的加速度反应谱，如图3所示，可见3条地震波的加速度反应谱与规范设计反应谱匹配良好，采用这3组地震波进行动力时程分析能较好地反映该工程场地地震动特征。计算时输入纵桥向与竖向地震组合，竖向地震动取水平地震动的0.6倍，按照《公路桥梁抗震设计规范》，取3组地震波计算所得结果的最大值作为动力时程分析的最终结果。

图2 地震波加速度时程Fig.2 Acceleration Time History of Seismic Wave

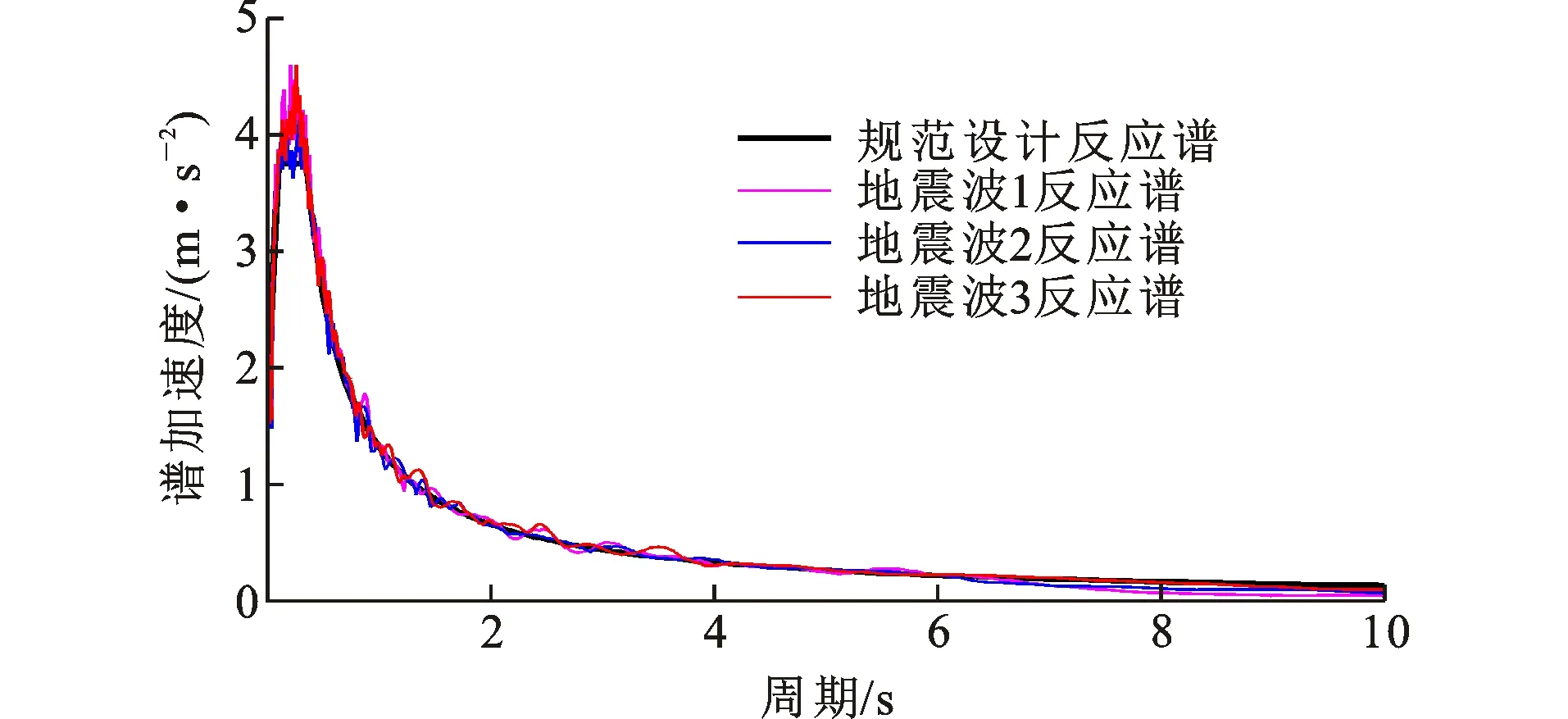
图3 地震波对应的反应谱与规范设计反应谱Fig.3 Response Spectrum Corresponding to Seismic Wave and Code Design Response Spectrum

2 动力特性分析与减震方案

2.1 动力特性分析

为了给桥梁黏滞阻尼器减震方案提供参考，采用里兹法计算结构的动力特性，表1汇总了前10阶结构自振频率、振型参与质量和振型主要特性。

表1 桥梁结构振型Table 1 Vibration Mode of Bridge Structure

由表1可知，由于桥梁跨径较大，横桥向刚度低于竖向刚度，前3阶振型均为横桥向振动。主梁纵飘振型出现在第4阶，振型参与质量达到纵桥向的45.31%，对桥梁纵桥向振动贡献较大，起主导作用，与文献[15]的结论一致，为了控制主梁在地震作用下的纵桥向位移，拟在主梁上设置黏滞阻尼器。

2.2 黏滞阻尼器减震方案设计

黏滞阻尼器利用活塞在油缸中运动时，活塞前后面的压力差产生阻尼力，活塞在油缸中往复运动来耗能。采用简化Maxwell模型对黏滞阻尼器进行模拟，阻尼器活塞运动速度和阻尼力之间的关系为

Fd=Cd|Ud|ξsgn(Ud)

(1)

式中：Fd为阻尼力；Ud为阻尼器活塞运动速度；Cd为阻尼系数；ξ为阻尼指数；sgn(·)为符号函数。

典型的黏滞阻尼器一般构造与不同阻尼指数ξ的滞回曲线形状在文献[5]中做了详细介绍，这里不再赘述。从抗震角度，阻尼指数ξ一般在0.2～1.0之间[5]，从目前已经在实际工程中安装的阻尼器来看，ξ一般取值集中在0.2～0.4[5,13-14,16]，Cd取值较为离散。比如东海大桥的黏滞阻尼器阻尼指数为0.3[5]，阻尼系数为10 000 kN·(m·s-1)-ξ；虎门二桥坭洲水道桥的黏滞阻尼器阻尼指数为0.3[13]，阻尼系数为6 000 kN·(m·s-1)-ξ；南宁大桥的黏滞阻尼器阻尼指数为0.35[14]，阻尼系数为2 000 kN·(m·s-1)-ξ。由于每一座桥梁的动力特性与所处地震环境有其独特性，因此需要对具体工程进行具体分析。

由式(1)可知，黏滞阻尼器的阻尼力与活塞运动速度有关，选择有较大相对位移的位置处安装黏滞阻尼器，既能对地震做出敏感反应，又可在足够大的位移上滞回耗能；同时，阻尼器安装处应能提供足够大的刚度，以避免在地震作用下被破坏或者随主梁一起振动，降低减震的效果。中承式钢管混凝土拱桥交界墩一般较高(本工程约22 m)，纵桥向刚度明显小于拱肋，在地震作用下拱肋纵桥向位移小，因此，主梁减震黏滞阻尼器选择安装在拱肋处，如图4所示。主梁在拱肋位置处开孔，以使主梁独立于拱肋而不与其接触，并设置4个纵桥向黏滞阻尼器与拱肋下弦相连来限制主梁地震位移，如图5所示。需要注意的是，本工程中两端节点板为单耳座，故黏滞阻尼器两端均为双耳环，阻尼器具体尺寸见图6，主要由耳环、缸体、连接筒以及防尘罩组成，其内部构造详见文献[5]。

图4 半漂浮体系中承式钢管混凝土拱桥上黏滞阻尼器立面布置Fig.4 Elevation of Viscous Dampers on Semi-floating System Half Through Concrete-filled Steel Tubular Arch Bridge

图5 支座与阻尼器平面布置Fig.5 Plane Layout of Support and Damper

图6 阻尼器示意图(单位：mm)Fig.6 Schematic Diagram of Damper (Unit:mm)

3 黏滞阻尼器参数分析与选取

抗震设计的主要目的就是控制关键构件的关键截面内力或位移不超过规范要求，对于中承式钢管混凝土拱桥，由于拱肋一般刚度较大，在地震作用下拱肋位移较小，因此控制因素主要是拱肋的内力状态、主梁的位移以及阻尼器连接构件的局部应力。拱肋的内力控制因素包括拱顶、L/4(L为拱桥纵向跨径)、拱脚等关键截面的轴力、剪力与弯矩等，主梁的位移控制因素包括梁端伸缩缝的容许位移、支座的容许位移、主梁与拱肋之间的容许相对位移以及主梁纵桥向位移引起的吊杆(一般为短吊杆)倾斜角度容许值，阻尼器连接构件的局部应力控制因素主要包括拱肋局部应力、主梁局部应力以及连接耳板的局部应力。经计算分析，各主要控制因素对应的阻尼器位移与内力容许值如表2所示，值得注意的是，根据《公路桥梁抗震设计规范》(JTG/T 2231-01—2020)第3.6.1条，表2中位移已考虑了50%的均匀温度作用效应。各类控制因素容许值的最小值即为阻尼器设计的控制值，据此确定阻尼器参数。由表2可知， 阻尼器纵桥向位移容许值为40 mm，而阻尼器内力控制值为900 kN，同时满足位移与内力容许值要求的参数范围为黏滞阻尼器参数的可选范围。

表2 阻尼器设计的主要控制因素Table 2 Main Control Factors for Damper Design

为了获得满足结构位移与内力要求的黏滞阻尼器参数，参考前文所述已经在工程中实际使用的阻尼器参数，对阻尼指数ξ与阻尼系数Cd进行参数分析。选取阻尼指数ξ试算值为0.2、0.3、0.4，选取阻尼器阻尼系数Cd试算范围为500～4 000 kN·(m·s-1)-ξ，可以计算得到地震作用下的桥梁位移与内力响应时程，由于控制因素往往为绝对值最大值，将阻尼指数为0.2、0.3、0.4时的梁端纵桥向位移与阻尼器轴力绝对值最大值结果分别汇总，结果如图7～9所示。

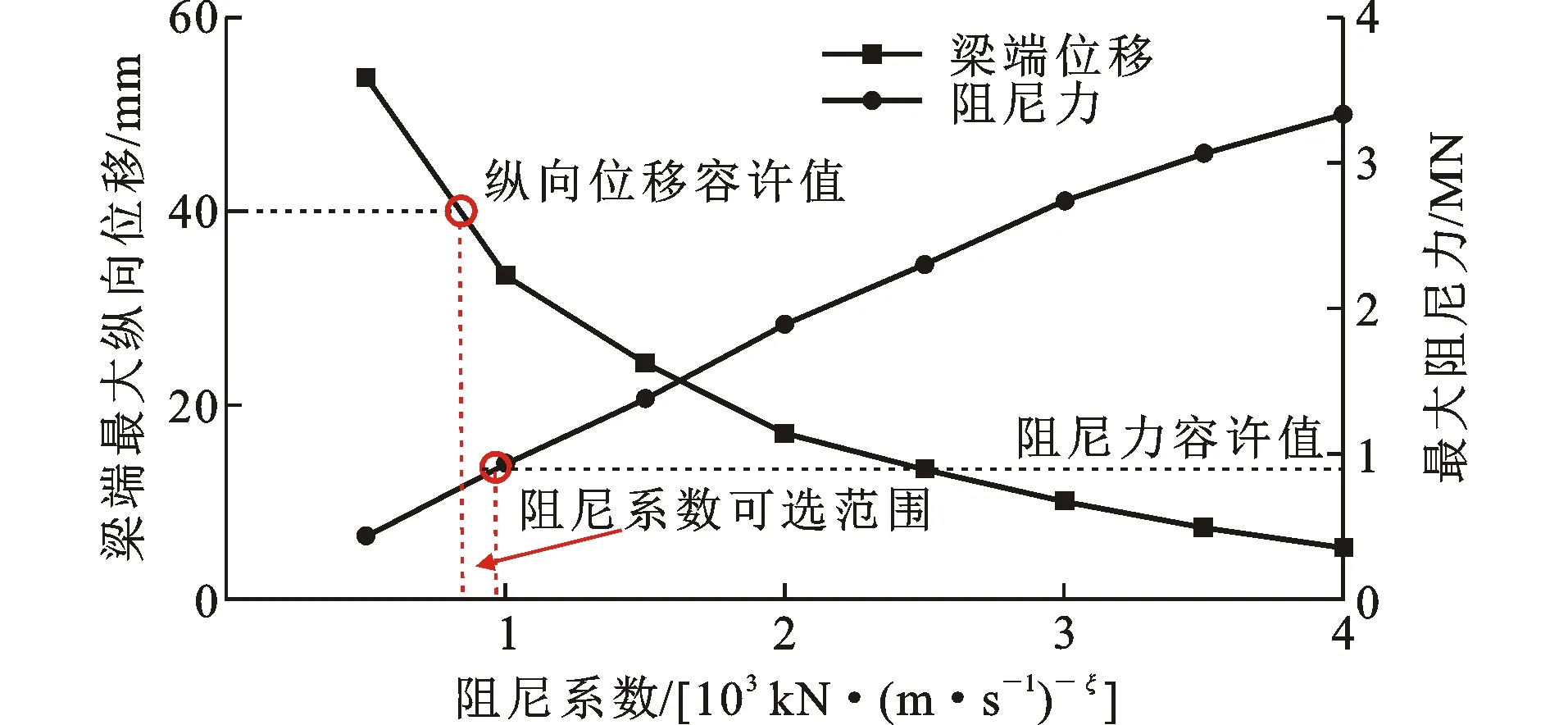
图7 阻尼指数ξ=0.2时阻尼系数Cd可选范围Fig.7 Optional Range of Damping Coefficient Cd when Damping Index ξ=0.2

图8 阻尼指数ξ=0.3时阻尼系数Cd可选范围Fig.8 Optional Range of Damping Coefficient Cd when Damping Index ξ=0.3

图9 阻尼指数ξ=0.4时阻尼系数Cd可选范围Fig.9 Optional Range of Damping Coefficient Cd when Damping Index ξ=0.4

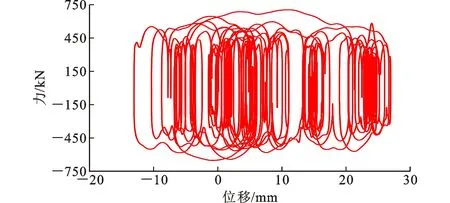
从图7～9可以看出：阻尼指数与阻尼系数会显著影响梁端最大纵桥向位移响应与阻尼器轴力响应；对相同的阻尼指数，梁端最大纵桥向位移响应随着阻尼系数的增大呈非线性减小，最大阻尼力响应随着阻尼系数的增大几乎呈线性增大。阻尼指数越大(ξ变化范围为0.2～0.4)，同时满足梁端位移与阻尼力要求的阻尼系数可选范围越大。图7～9水平方向虚线表示的是梁端纵桥向位移容许值或阻尼力容许值，即水平黑色虚线下方的阻尼系数可满足纵桥向位移要求或阻尼力要求，而图7～9竖直方向虚线之间的阻尼系数同时满足纵桥向位移要求与阻尼力要求，即为该阻尼指数条件下的阻尼系数可选范围。阻尼指数ξ=0.2时，阻尼系数Cd可选范围为800 kN·(m·s-1)-ξ

4 减震效果分析

将选定的阻尼器参数输入MIDAS/Civil有限元模型中的Maxwell黏滞阻尼器参数，经计算分析可得设置阻尼器后的桥梁地震响应，与未设置阻尼器时的地震响应结果进行对比，可以分析得到黏滞阻尼器对半漂浮体系中承式钢管混凝土拱桥的减震效果。图10与图11分别为梁端纵桥向位移响应与拱顶纵桥向位移响应时程对比，表3列出了桥梁关键部位位移时程响应最大值结果。

图10 梁端纵桥向位移时程对比Fig.10 Time History Comparison of Longitudinal Displacement of Girder End

由图10、图11以及表3可知：设置阻尼器前梁端纵桥向位移为76.8 mm，远大于伸缩缝处主梁纵桥向位移限值40 mm，设置黏滞阻尼器是十分必要的；设置阻尼器以后，梁端纵桥向位移显著减小为32.1 mm(减少了约58%)，满足梁端纵桥向位移要求，这说明本文提出的黏滞阻尼器设置方案与参数能起到很好的减震效果。同时，由于黏滞阻尼器将主梁的地震力传递给拱肋，导致阻尼器处拱肋纵桥向位移由5.7 mm变化为8.0 mm，增大了约40%，L/4处拱肋纵桥向位移增大约20%，拱顶纵桥向位移增大约17%，而拱顶竖向位移略有减小，减小了约3.0%，但由于拱肋刚度较大，拱肋位移响应的绝对值变化相对于恒载与其他活载效应来说较小。

图12为地震作用下黏滞阻尼器的阻尼力时程，最大阻尼力为700 kN，小于阻尼器连接件的容许值900 kN，验证了本文所用方法选取的阻尼器参数满足最大阻尼力要求。表4汇总了拱肋关键截面(拱顶、L/4处、阻尼器位置处与拱脚)的最大内力响应。

图12 黏滞阻尼器阻尼力时程Fig.12 Damping Force Time History of Viscous Damper

由表4可知：在地震作用下，设置黏滞阻尼器以后，除拱顶处拱肋轴力略有减少外，其余各处拱肋轴压力有所增加(增幅为6%～22%)，其中拱脚上弦轴力增加最多(约22%)； 各处拱肋的剪力响应均有所增大(增大10%～41%)；各处拱肋的弯矩响应均增大(增大16%～43%)，其中拱脚下弦增加最多，增大约43%，但弯矩绝对值不大，地震弯矩响应引起的拱肋钢管应力约为12.3 MPa。经验算，偶然作用组合下拱肋钢管的最大应力为173.5 MPa，小于钢材Q345的容许应力。

表4 拱肋关键截面最大内力响应比较Table 4 Comparison of Maximum Internal Force Response of Key Sections of Arch Rib

黏滞阻尼器的滞回曲线越饱满，耗能效果越好。以地震波1为例，选取的黏滞阻尼器的滞回曲线如图13所示，可以看出黏滞阻尼器的耗能效果良好。

图13 黏滞阻尼器滞回曲线Fig.13 Hysteretic Curve of Viscous Damper

5 结语

(1)半漂浮体系中承式钢管混凝土拱桥的纵飘振型出现较早，振型参与质量所占比重大，应设置黏滞阻尼器控制主梁地震位移，黏滞阻尼器参数选取范围由主梁端纵桥向容许位移、阻尼器连接构件所能承受的容许阻尼力共同确定。

(2)对相同的阻尼指数，梁端最大纵桥向位移响应随着阻尼系数的增大呈非线性减小，最大阻尼力响应随着阻尼系数的增大几乎呈线性增大。

(3)阻尼指数越大(ξ变化范围为0.2～0.4)，同时满足梁端位移与阻尼力要求的阻尼系数可选范围越大。

(4)对本工程案例，设置黏滞阻尼器以后，梁端纵桥向位移响应显著减少(约58%)，拱顶纵桥向位移有所增加(约17%)， 除拱顶处拱肋轴力略有减少外，其余各处轴力、剪力与弯矩均有所增加，但内力响应绝对值不大。