肼及其衍生物与HNO2反应的定量构效关系

聂 江，杨舒茗，李明明，杨雅雅，刘晓娟，欧阳应根，肖松涛

中国原子能科学研究院 放射化学研究所，北京 102413

U/Pu分离是PUREX流程共去污循环的关键步骤，此步骤通过选择合适的还原反萃试剂对Np、Pu价态进行调整，实现U、Pu的分离，控制Np的走向。广泛使用的U(Ⅳ)/肼还原剂存在一定的不足，开发新型有机无盐还原剂成为PUREX流程改进的一个重要方向。中国原子能科学研究院何辉等[1]基于N,N-二甲基羟胺/单甲基肼体系发展的PUREX二循环流程是较典型的无盐化改进流程。

强放射性条件下HNO3分解等过程使体系中存在HNO2[2]。HNO2影响料液中Np、Pu以及部分裂片元素的价态和形态，从而影响Pu的收率、Np的走向以及净化效果。普遍采用向还原剂体系中引入HNO2清扫剂来消除这些影响。最常用的HNO2清扫剂是肼，但肼与HNO2反应会生成叠氮酸[3]。因此，寻找新的HNO2清扫剂[4]、降低叠氮酸的生成量，对于进一步优化PUREX流程，有着十分重要的意义。

Perron等[5]在高氯酸介质中研究了肼过量时HNO2和肼反应的产物和反应动力学，认为肼与HNO2之间的反应是N-亚硝化反应；Phelan等[6]用质谱分析了15N标记的肼和过量HNO2反应生成的N2和N2O中15N的分布情况，提出了一种环状的叠氮酸作为中间产物的反应机理；Stedman等[7]对HNO2和苯肼的反应动力学及反应机理进行了研究，认为该反应是由[NO]+或者[H2NO2]+与芳基肼鎓离子控制的亚硝化反应。上述工作对肼及其衍生物与HNO2之间的反应机制进行了研究，但未讨论肼及其衍生物的分子结构与其反应活性之间的关系。

定量构效关系(quantitative structure activity relationship, QSAR)是定量描述有机物结构和活性之间相互关系的一种方法，通过选择表征反应活性的参数以及分子结构描述符，结合数理统计方法揭示化合物活性与其物理化学特征或者分子结构之间的定量变化规律，被广泛应用于药物设计、环境科学、化学等领域[8-15]。

本工作拟利用分光光度法测量肼及其衍生物与HNO2的半反应时间，结合肼及其衍生物量化计算的结果，建立肼及其衍生物与HNO2反应的定量构效关系模型，以期为新的HNO2清扫剂的选择提供指导。

1 实验部分

1.1 试剂与仪器

所有试剂均为市售分析纯。

SFA-20 Rapid Kinetics Accessory流动注射装置，HI-TEC公司，示意图示于图1；UV Power紫外可见分光光度仪，北京莱伯泰科仪器股份有限公司；恒温水浴槽，宁波新艺超声设备有限公司。

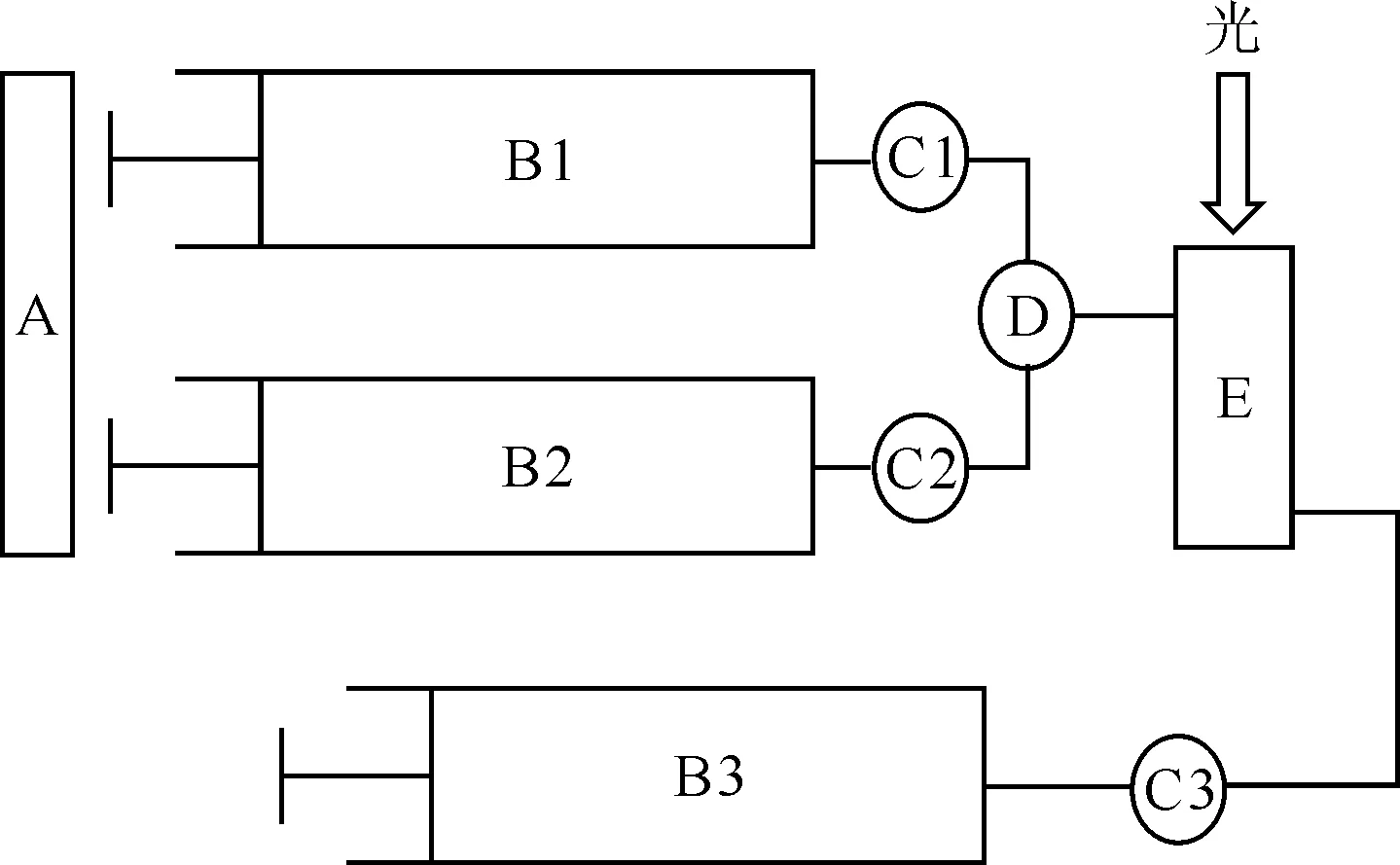
A——泵，B1、B2、B3——注射器，C1、C2、C3——阀门，D——混合器，E——比色皿图1 流动注射装置示意图Fig.1 Schematic diagram of stopped-flow injection device

1.2 实验方法

利用恒温水浴槽控制反应温度为(1.0±0.5) ℃。利用流动注射装置将肼和NaNO2快速混合，并用分光光度仪测量一段时间内HNO2的吸光度随时间的变化。实验过程以及数据处理方法如下：

(1) 配制Ⅰ、Ⅱ 两种反应溶液，其中，反应溶液Ⅰ为0.01 mol/L NaNO2溶液；反应溶液Ⅱ为0.1 mol/L肼(溶于1.2 mol/L HClO4)；

(2) 将Ⅰ、Ⅱ两种溶液置于温度为1 ℃的水槽中恒温15 min；

(3) 用两支注射器分别取Ⅰ、Ⅱ两种反应液各20 mL，利用流动注射装置，每间隔几秒向比色皿中等体积注射Ⅰ、Ⅱ两种液体(混合后肼的浓度为0.05 mol/L，NaNO2浓度为0.005 mol/L，HClO4浓度约为0.6 mol/L)，与此同时分光光度仪在371 nm处对HNO2的吸光度开始动力学测量；

(4) 由动力学测量得到吸光度(A)随时间(t)的变化，绘制A-t曲线。根据A-t曲线中HNO2的起始吸光度A0和HNO2的标准曲线确定HNO2起始浓度c0(实验中出现A0超出HNO2标准曲线范围的情况，考虑是溶液混合不均匀引起的，此时将标准曲线外推确定c0)，再由标准曲线确定1/2c0所对应的吸光度，并结合A-t曲线求出半反应时间t1/2。最终得到的半反应时间为多次测量的平均值。

1.3 计算方法

利用GaussView构建肼及其衍生物的初始结构(图2)，使用Gaussian09的密度泛函B3LYP方法、6-311+(3d，3p)基组对化合物进行结构优化和能量计算，得到能量最低的稳定结构及各分子的偶极矩。计算振动频率，所有分子的振动频率计算值均无虚频，说明获得的是最稳定构型。考虑到溶剂对反应物分子的几何构型、电子结构、稳定性等方面均会产生一定的影响[16-17]，为了更真实地反映溶液中分子的真实行为，在此基础上增加关键词scrf(SMD，solvent=water)，即选择水作为溶剂，用基于极化连续介质模型的自洽场方法对计算进行修正。

使用Gaussian09和HyperChem进一步计算结构优化后的分子的轨道跃迁能、疏水性参数、水合能、分子体积、分子表面积(估算)、分子表面积(网格化)和折射系数等结构参数。

综上，利用Gaussian09和HyperChem计算获得了肼及其衍生物的分子总能量、偶极矩、轨道跃迁能、疏水性参数、水合能、分子体积、分子表面积(估算)、分子表面积(网格化)和折射系数等结构参数。

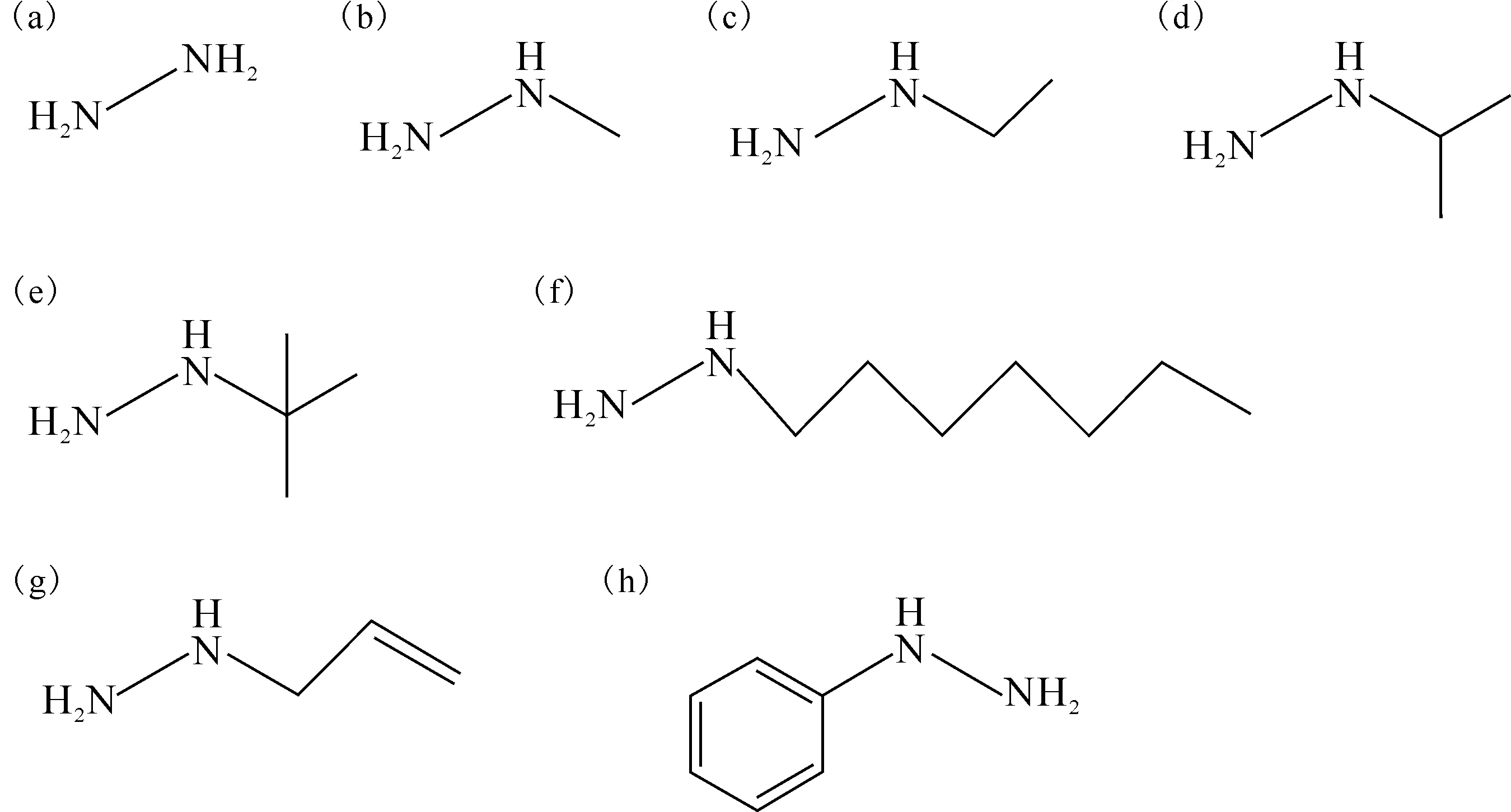
(a)——肼，(b)——甲基肼，(c)——乙基肼，(d)——异丙基肼，(e)——叔丁基肼，(f)——正庚基肼，(g)——烯丙基肼，(h)——苯肼图2 肼及其衍生物的结构式Fig.2 Hydrazine and its derivatives’ structures

2 实验结果与模型建立

2.1 半反应时间

通过实验测量得到HNO2吸光度随时间的变化曲线示于图3，标准曲线示于图4。HNO2与肼及其衍生物的半反应时间列入表1。从表1可以看出：

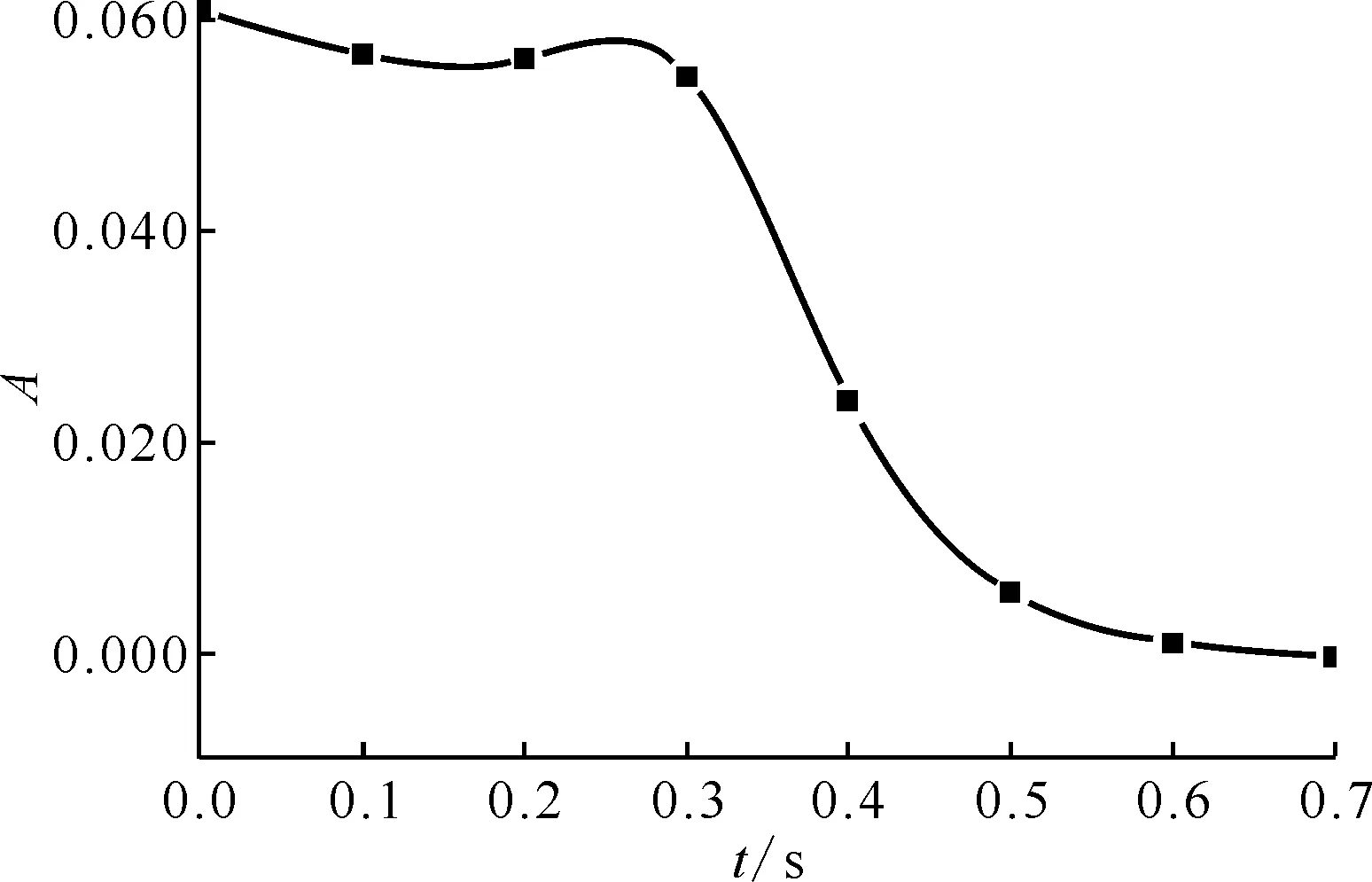
图3 HNO2的吸光度随时间的变化(与肼反应)Fig.3 Absorbance of HNO2 changing over time (reaction with N2H4)

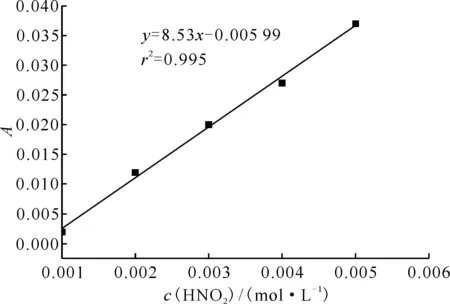
图4 HNO2标准曲线Fig.4 Standard curve of HNO2

(1) 正庚基肼与HNO2的半反应时间远远大于其它几种衍生物的，这可能是由于其水溶性较差，仅仅通过流动注射装置难以使其与HNO2在短时间内均匀混合，导致测得的半反应时间远远大于其它衍生物的；

(2) 对比肼、甲基肼、乙基肼、异丙基肼及叔丁基肼与HNO2的半反应时间可知，对于含饱和支链的衍生物，半反应时间随着支链碳原子数的增加而增加；

(3) 对比异丙基肼和烯丙基肼与HNO2的半反应时间可知，具有不饱和支链的衍生物能与HNO2更快反应。

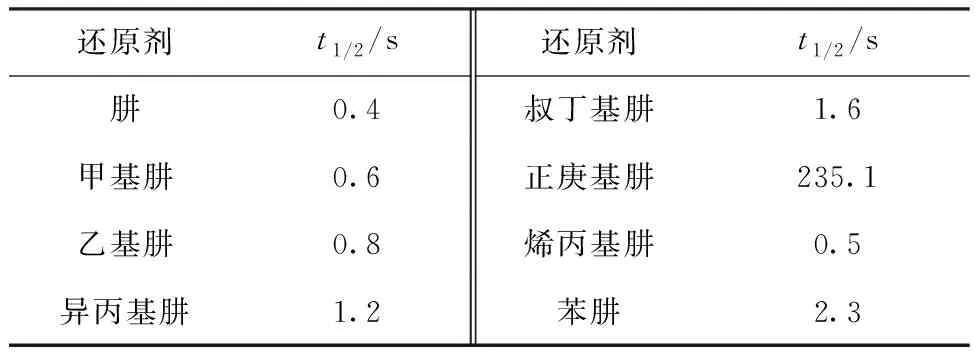
表1 肼及其衍生物与HNO2反应的半反应时间Table 1 Half-reaction time of hydrazine and its derivatives with HNO2

2.2 量化参数

利用Gaussian09 的密度泛函B3LYP方法、6-311+(3d，3p)基组，同时考虑水作为溶剂对分子的影响，对肼、甲基肼、乙基肼、异丙基肼、叔丁基肼、正庚基肼、烯丙基肼和苯肼共8种化合物进行结构优化，计算分子总能量(E)、偶极矩(μ)、最高占据轨道能(EHOMO)、最低未占据轨道能(ELUMO)以及轨道跃迁能(ΔE)。在对输出文件进行频率检查时发现，肼和乙基肼的频率出现负值，即出现虚频，此时所得的构型并不是能量最低的稳定构型，为了消除虚频，添加关键词opt=calcall(表示每一步优化都计算力矩阵，力矩阵可以指引优化的方向，虽然在一定程度上增加了计算负担，但有效消除了虚频)。进一步使用HyperChem软件计算经Gaussian09 进行结构优化后的各化合物的疏水性参数(lgP)、水合能(EH)、分子体积(V)、分子表面积(估算)(A)、分子表面积(网格化)(G)、折射率(R)以及相对分子质量(Mr)。将从上述两个软件中取得的结构参数汇总列于表2。

2.3 统计回归建模

正庚基肼由于水溶性较差，测得的半反应时间远远大于其它衍生物的，在模型建立阶段将其从样本中剔除。在去掉正庚基肼所对应的数据后，使用SPSS软件对上述各结构参数与半反应时间进行相关性分析，得到Pearson相关系数矩阵列于表3。

为了分析各结构参数与半反应时间之间可能存在的其它相关关系，以半反应时间为因变量，分别对其余变量作散点图，结果示于图5。

由相关系数矩阵和散点图可知，最低未占据轨道能、水合能、分子表面积(估算)、轨道跃迁能、最高占据轨道能与半反应时间之间的相关性较差，考虑将它们剔除。

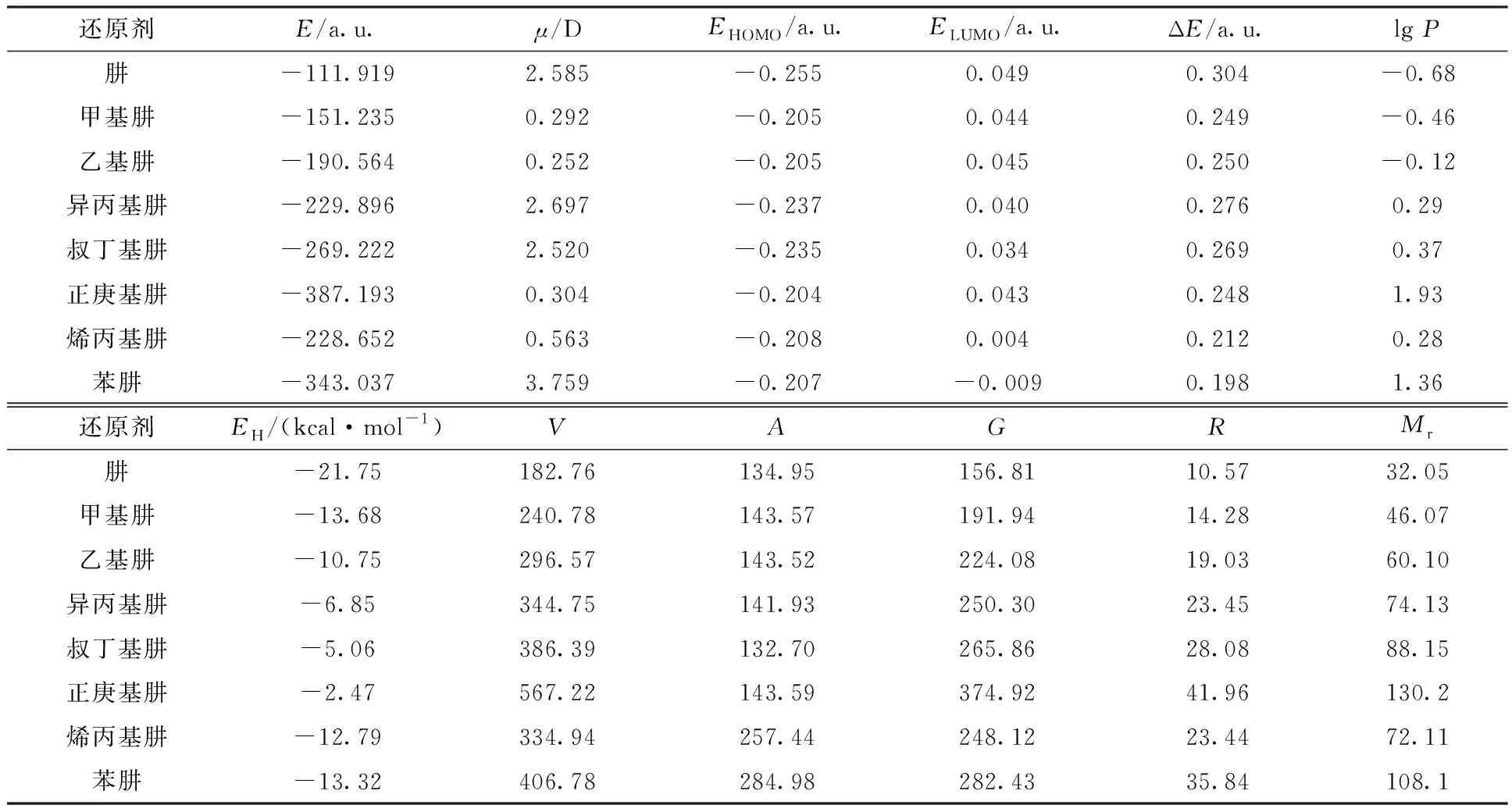
表2 肼及其衍生物的量化参数Table 2 Quantization parameters of hydrazine and its derivatives

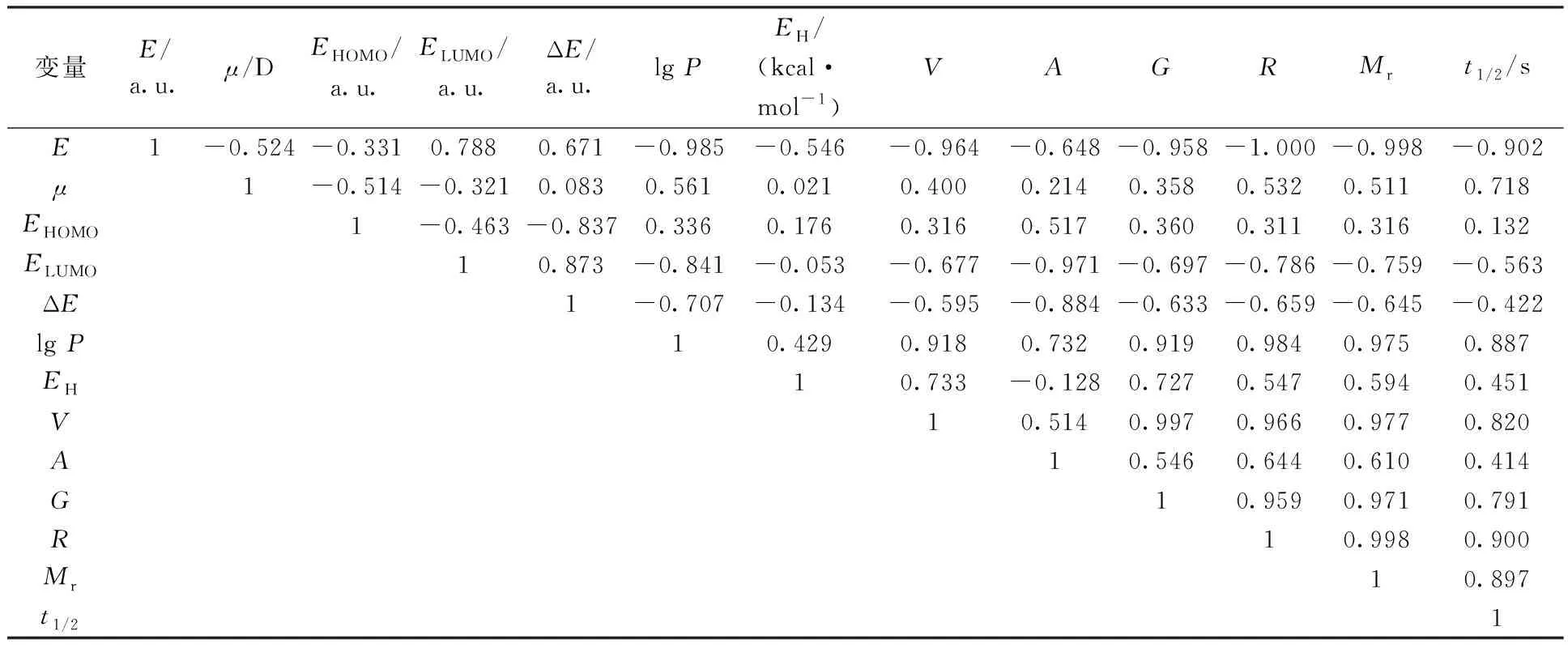
表3 Pearson相关系数矩阵Table 3 Pearson correlation matrix

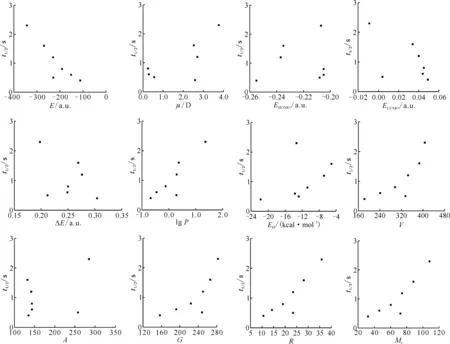
图5 量化参数与半反应时间之间的散点图Fig.5 Scatter plots of quantization parameters and half-reaction time

将其余变量与半反应时间之间的相关系数按照绝对值从大到小的顺序排列，结果列于表4。由表4可见，分子总能量与半反应时间之间的线性相关性最强，考虑其它几个变量与分子总能量之间的相关性(表5)可知，折射率、相对分子质量、疏水性参数、分子体积、分子表面积(网格化)与分子总能量之间均存在很强的线性关系，即可以用分子总能量代替这部分变量，故将这些变量剔除。经上述操作后，最终将初始的12个变量筛选至2个变量：分子总能量E和偶极矩μ。

表4 其余变量与半反应时间之间的相关系数Table 4 Pearson correlation between half-reaction time and other variables

表5 其余变量与分子总能量之间的相关系数Table 5 Pearson correlation between E and other variables

根据偶极矩对半反应时间的散点图，考虑在模型中增加μ2项，使用分子总能量E、偶极矩μ和μ2作为自变量，调用Matlab R2021a统计工具箱中的“regress()”命令对半反应时间进行多元线性回归(置信水平α=0.05)，得到以下两个模型列于表6、表7。

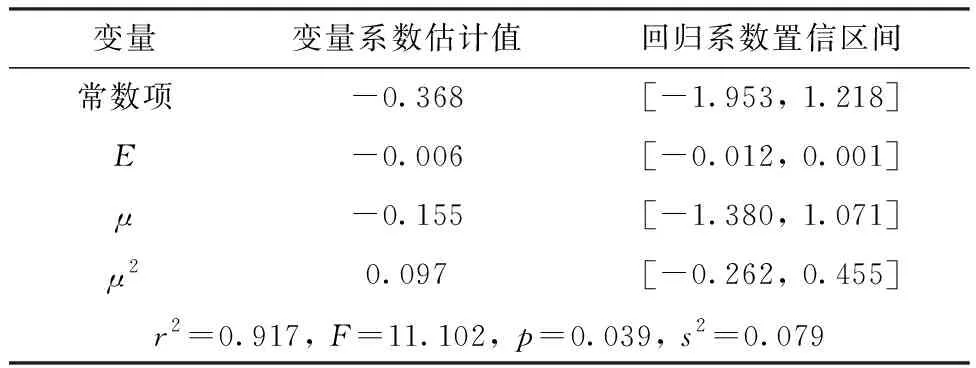
表6 模型1计算结果Table 6 Results of model 1

表7 模型2计算结果Table 7 Results of model 2

由表6、7可知，这两个模型的r2均大于0.9，但是μ和μ2项的回归系数的置信区间均包含零点，即这两项对半反应时间的影响不显著，为此考虑用E单独进行回归(表8)。该模型的残差分析示于图6。由图6可知，除了烯丙基肼外，其余肼及衍生物的残差均离零点较近，且残差的置信区间均包含零点，说明此模型能对原始数据进行较好地解释，但是不能较好地预测烯丙基肼。

表8 模型3计算结果Table 8 Results of model 3

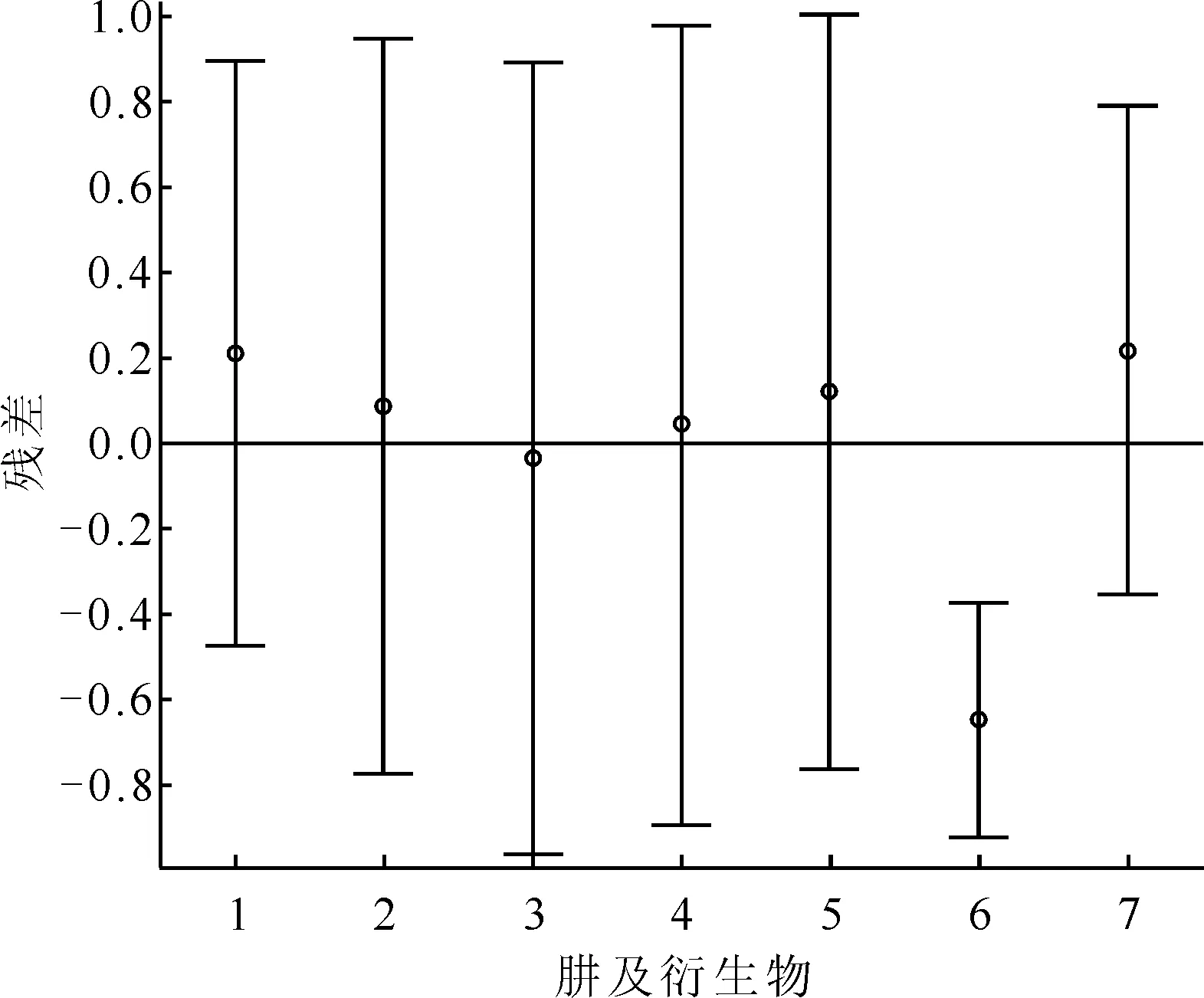
1——肼，2——甲基肼，3——乙基肼，4——异丙基肼，5——叔丁基肼，6——烯丙基肼，7——苯肼图6 模型3的残差分析图Fig.6 Residual analysis plot of model 3

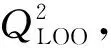
表9 留一法交叉验证结果Table 9 Results of leave-one-out method

3 结 论

对肼及其衍生物与HNO2的反应进行研究可以为其在PUREX流程中的进一步应用提供指导。本工作借助流动注射装置，使用分光光度法测定了肼及其衍生物与HNO2反应的半反应时间，结合量化计算的结果，构建了肼及其衍生物与HNO2反应的定量构效模型，经过检验，所得到的模型具有良好的内部预测能力和稳定性。模型显示，分子总能量E是该反应最重要的影响因素，半反应时间大致随E的增加而增加。