风电场自动电压控制中风机和静止无功发生器的无功分配研究
朱建华 何卓林 闫伟军 姜继琛 杨海峰
风电场自动电压控制中风机和静止无功发生器的无功分配研究
朱建华1何卓林1闫伟军2姜继琛3杨海峰4
(1. 润电能源科学技术有限公司,郑州 450000;2. 国网伊犁伊河供电有限责任公司特克斯县供电公司,新疆 特克斯 835599; 3. 华润新能源(唐河)有限公司,河南 唐河 473400;4. 华润新能源(临颍)有限公司,河南 临颍 462600)
自动电压控制(AVC)系统的投入对保证风电场的电压稳定有重要作用,现有研究对风电场的自动电压控制无功分配策略缺乏深入分析。本文在现有自动电压控制无功分配模式的基础上,采用含有静止无功发生器(SVG)和风力发电机的小干扰模型,分析自动电压控制无功分配策略对风电场稳定性的影响。该方法计及自动电压控制系统中无功分配模式对风电动态稳定性的影响,可指导实际生产。通过对某实际风力发电机的算例分析,验证了方法的有效性。
自动电压控制(AVC);静止无功发生器(SVG);风力发电机;无功分配
0 引言
自动电压控制(automatic voltage control, AVC)对保证风电场电压稳定有重要意义,在风电场得到广泛应用[1-4]。目前,国内对风电场自动电压控制的研究主要分为两个方向:①从电力系统稳定角度分析风电自动电压控制的意义;②风电场场站级别的自动电压控制研究。文献[5]将模型预测控制应用到自动电压控制策略中,为实际自动电压控制策略提供了一种可行的技术路线。文献[6]研究新能源场站的自动电压控制策略,为解决高比例可再生能源系统电压控制提供了一种解决方法。文献[7]研究风机和静止无功补偿快慢系统协调控制,为实际风电场的无功调节提供了良好的技术范例。文献[8]研究了静止无功补偿器(static var compensator, SVC)在风电场自动电压控制中的应用。文献[9]介绍风电场自动电压控制系统的架构和内部逻辑,为风电场自动电压控制的工程研究提供了可供参考的技术框架。
近年来,由于接入电力系统的新能源容量不断增大,其对系统电压稳定的影响也随之变大。为改善风电并网影响系统电压稳定的问题,静止无功发生器(static var generator, SVG)构成风电场无功配套电源的重要组成部分,自动电压控制进而重新成为研究热点。文献[10]研究了风电场中静止无功发生器的参数测试和整定,但目前对风电场自动电压控制的研究多集中在与电网稳定相关的课题,关于风电场的风机和静止无功补偿的协调问题鲜有涉及。实际上两者的协调对于风电场经济运行和稳定分析都有重要影响,因此,需要对该问题进行深入分析,并提出相应的解决方案,进而为风电场日常运行提供有效的技术指导。
针对上述问题,本文采用包含自动电压控制的风机和静止无功发生器模型,分析自动电压控制分配策略对风电场稳定性的影响。在研究过程中,考虑到风电场电压控制的主要环节是自动电压控制、风机、静止无功补偿环节,将模型中的稳定约束作为计算边界条件,完成包含自动电压控制环节的风电场稳定计算。分析结论可为风电场自动电压控制确定无功分配策略提供参考。
1 自动电压控制模型
一种常见的风电场自动电压控制模型如图1所示。
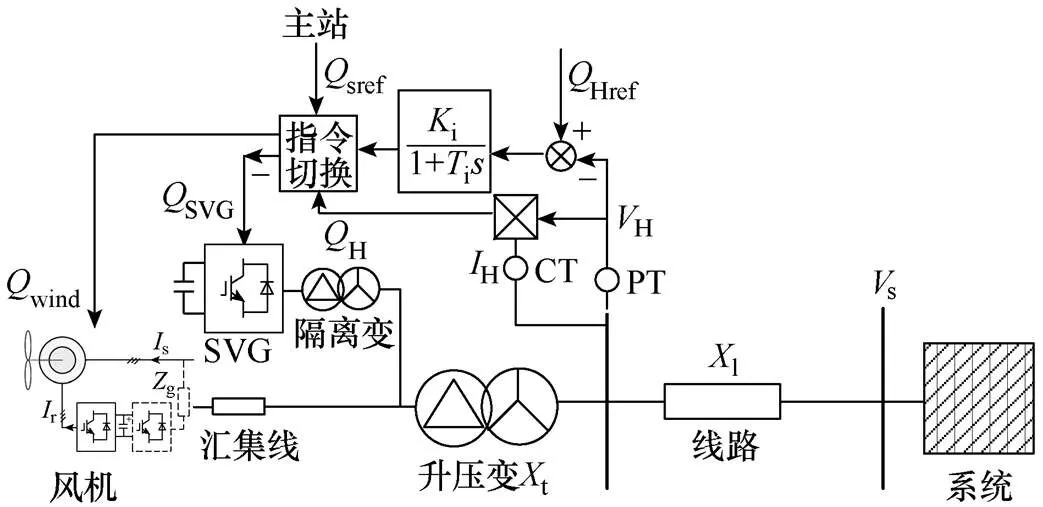
图1 风电场自动电压控制模型
从图1可以看出,风机自动电压控制环节主要包含两种控制模式:高压侧定电压控制模式和主站定无功控制模式。
第一种模式为高压侧定电压控制模式,控制输入信号为高压母线电压s,指令信号为高压侧电压参考值sref,i为电压控制环节放大倍数,i为电压环节采样时间常数,输出为无功信号参考指令。l为线路电抗,t为升压变压器电抗。H为高压侧电流,H为高压侧电压,Href为高压侧无功参考值。CT为电流互感器,PT为电压互感器。SVG为SVG输出的无功,wind为风机输出的无功,H为高压侧无功,sref为主站无功参考值。
第二种控制模式为主站定无功控制模式,在该控制模式下,无功指令由上一级主站给定,无功参考值直接与高压侧无功H相减,输出无功偏差值作为输入进入无功控制环节。
风电场自动电压控制系统计算出所需的无功量后,需要在风机和静止无功发生器之间进行分配,分配模式有三种:风机优先、静止无功发生器优先、风机和静止无功发生器均半。
对于风电场自动电压控制系统而言,可将静止无功发生器直接连接在升压变的低压母线上视为就地控制;而风机通过汇集线连接在升压变低压侧母线上,且风机分散在不同地理位置上,可视为远端分散控制。因此,不同的无功分配模型即为不同的控制策略,对风电场的动态稳定有重要影响。
2 小干扰模型
2.1 SVG模型
SVG的机电模型一般包含检测模块、控制运算模块及补偿输出模块。本节保留PI控制环节,对应的模型为
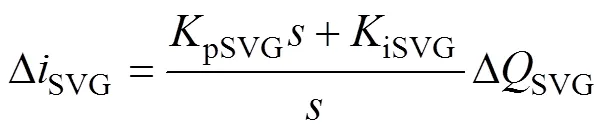
2.2 单台风机模型
风力发电机的模型比较复杂,本节模型忽略定子和转子电流动态部分、直流电压控制环节。单台风力发电机的电气相量图如图2所示。
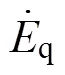
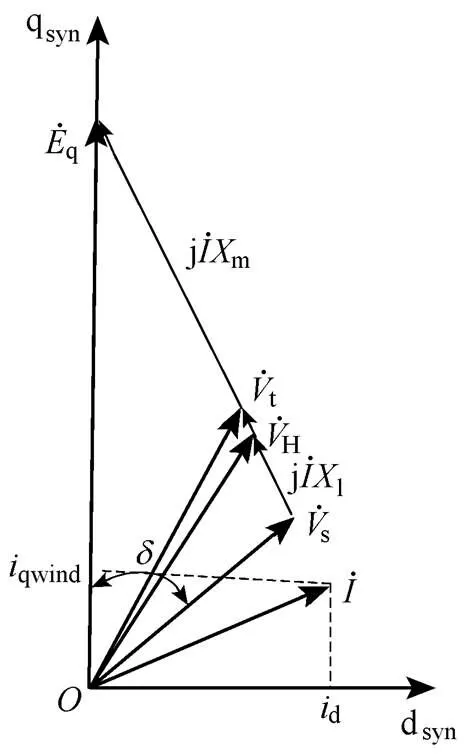
图2 单台风力发电机的电气相量图
根据图1,风机定子d轴和q轴电流可由下式计算,即


式中:s为系统母线电压;e为系统电抗和线路电抗之和;t为变压器电抗。
根据式(2)和式(3)对d和qwind进行线性化可得
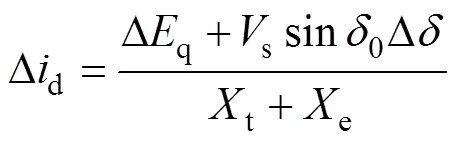
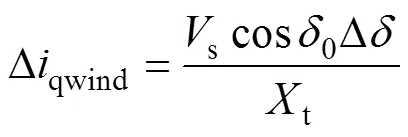
式中,带0的下角标表示该状态量在某稳态时的值,下同。
根据图2,可以得出机端电压q轴分量tq和d轴分量td分别为
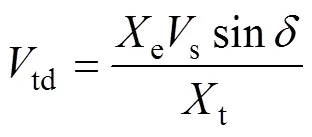
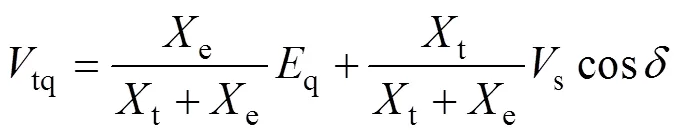
将式(6)和式(7)线性化可得
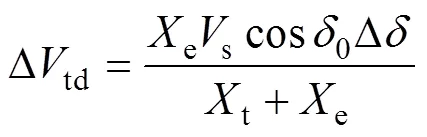

无功控制环模型[11]为
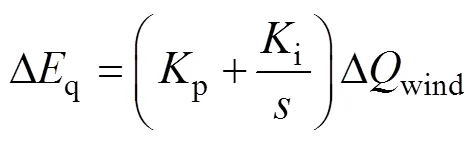
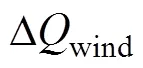
2.3 多台风机模型
将多台风力发电机等效为单台同步发电机,机端电压等效为升压变低压侧电压,汇集线和箱变都等效为等效发电机的内电抗。
等效的原则为:等效机的功率等于被等效发电机的总和;惯量等于各台风机的惯量之和;m为风机的等效电抗,即各台风机定子暂态电抗并联之后的电抗;PI控制环的参数等效前后保持一致。
等效的模型采用和单台风机一致的模型,对应模型电气相量图如图2所示。
2.4 高压侧模型
将风电场的多台风机等效为一台风机后,根据图1可以得出系统高压侧母线电压H和机端电压t关系为

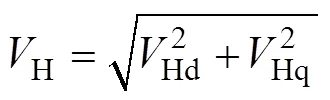
式中,qSVG为静止无功发生器q轴电流。
根据式(7)~式(12)对高压侧母线电压H进行线性化可得

其中
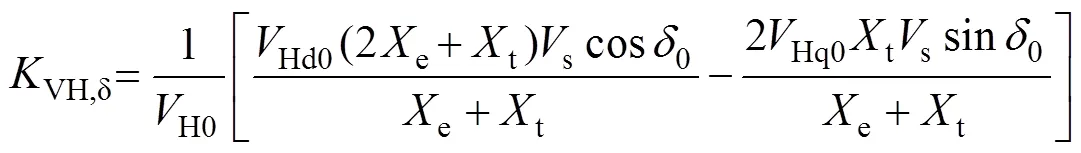
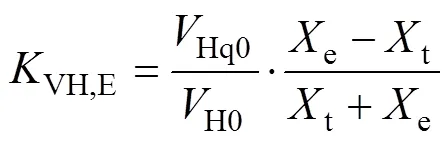
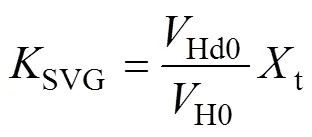
2.5 AVC模型
AVC的主要作用是将电压增量转化为无功,然后将无功分配给SVG和风机。
AVC的模型为

AVC中无功分配策略为
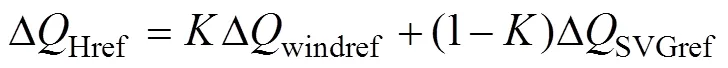
静止无功发生器输出无功的表达式SVG为
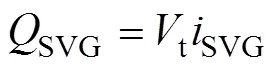
式中,SVG为静止无功发生器电流。
综合式(7)、式(9)和式(19)对静止无功发生器输出的无功进行线性化可得
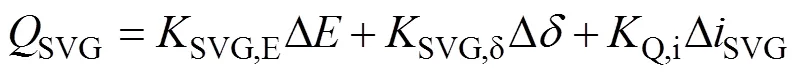
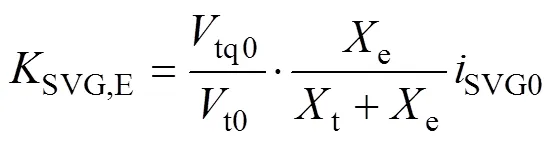
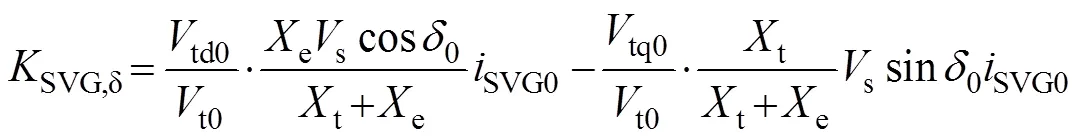

风机无功的表达式为

对风机无功进行线性化,可得
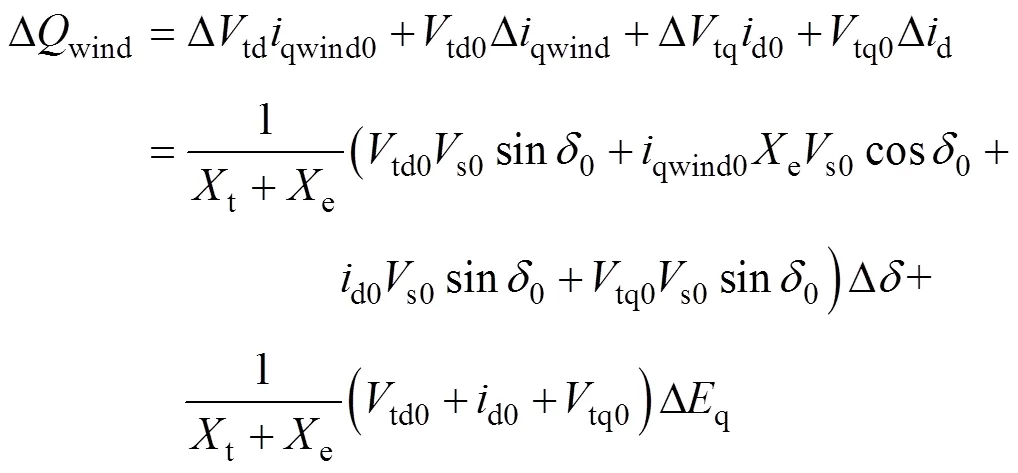
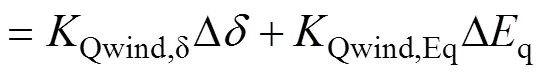
根据式(2)、式(10)、式(13)、式(17)、式(18)和式(25)建立包含AVC和SVG的风电场小干扰模型如图3所示。
图3中,当=1时,代表风机优先;若=0,则代表静止无功发生器优先;=0.5时,代表风机和静止无功发生器均半。
研究不同无功分配模式下稳定性的区别,采用如下方式计算图3所示模型的稳定性。

图3 含风机和静止无功发生器的小干扰模型
1)计算含风机和静止无功发生器的代数模型初值,计算出对应的稳态值。
2)根据式(1)~式(23)和稳态值计算出小干扰系数,搭建如图3所示的小干扰模型。
3)计算图3所示的小干扰模型的所有特征值,提取所有特征值中最大实部。
4)改变含风机和静止无功发生器的代数模型初值,重复步骤1)~3),得出风电场主要运行工况及对应主要运行工况的特征值最大实部。
3 仿真分析
为验证本文理论的有效性,在软件平台ANDES上建立仿真模型[12],模型参数如下:静止无功发生器容量为30Mvar,风电场容量为100MW,基准容量为100MV∙A,风机通过箱变从690V升压至35kV,然后通过升压变接入110kV电网,风机的等效电抗m=1.5p.u.;风机无功控制环节p=30,i=80,静止无功发生器的模型用PI控制器表示,pSVG=10,iSVG=30。
3.1 风机优先策略
设置AVC策略在风机优先模式下,即风电场主要运行在风机控制模式。风电场在运行过程中,有功出力受到风速的影响极大,所以有必要对风电场运行过程的主要出力工况进行模拟,以验证主要运行工况对自动电压控制系统的影响。图4为风机优先策略下风电场主要工况的特征值最大实部分布图。
从图4可以看出,在风机优先策略下,在风电场主要运行区域内,风电场系统基本上保持稳定。在无功恒定的前提下,稳定性随着有功出力的增多而逐渐变弱,稳定极限随着有功出力的增多先上升后下降,在0.5倍额定有功出力下系统最为稳定。在风电场有功恒定的前提下,从进相运行到滞相运行时,系统稳定性变弱。
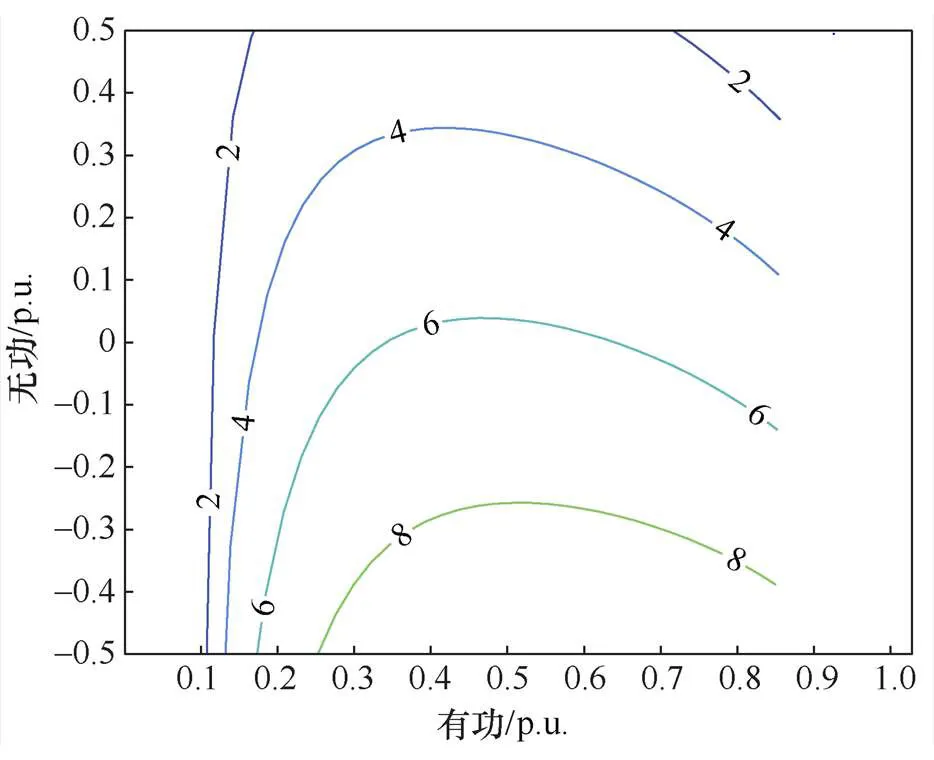
图4 风机优先策略下的特征值最大实部分布图
3.2 静止无功发生器优先策略
设置自动电压控制策略在静止无功发生器优先模式下,即风电场主要运行在静止无功发生器控制模式。计算条件与3.1节保持一致。图5为静止无功发生器优先策略下风电场主要工况的特征值最大实部分布图。
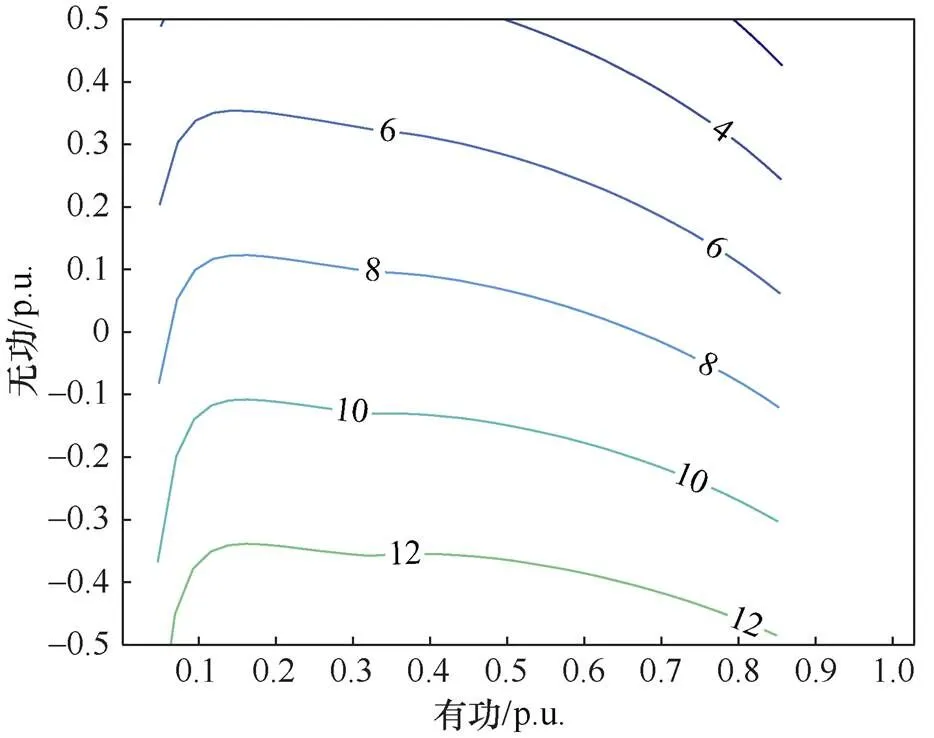
图5 静止无功发生器优先策略下的特征值最大实部分布图
从图5可以看出,在静止无功发生器优先策略下,在风电场主要运行工况,系统基本上保持稳定。与风机优先策略的特征值对比,静止无功发生器优先策略的稳定性更强,主要原因是静止无功发生器与高压侧母线电气距离更近,且为集中调控。在无功恒定的前提下,稳定性随着有功出力的增多先上升后下降,风电场系统在0.13倍额定有功时最为稳定。在有功恒定的前提下,从进相运行到滞相运行变化时,系统稳定性变弱。
3.3 风机和静止无功发生器均半策略
设置自动电压控制策略在静止无功发生器和风机均半模式下,即风电场运行在风机和静止无功发生器同时调整模式。计算条件与3.1节保持一致。图6为静止无功发生器和风机均半控制策略下风电场主要工况的特征值最大实部分布图。
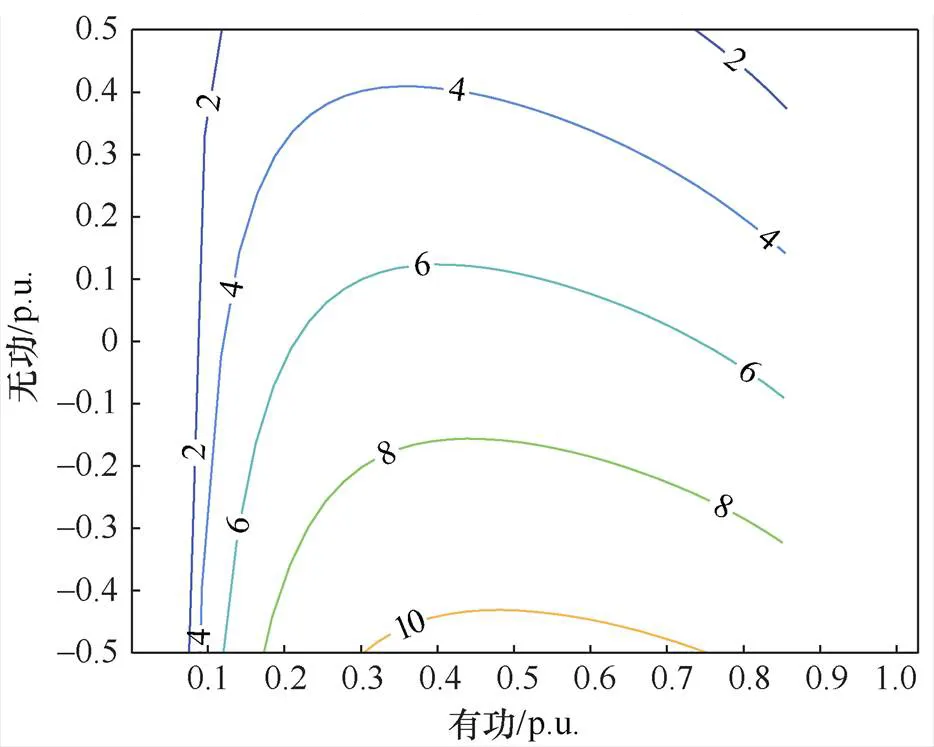
图6 静止无功发生器和风机均半策略下的特征值最大实部分布图
从图6可以看出,在静止无功发生器和风机均半策略下,在风电场主要运行区域内,全场基本上保持稳定。与其他两种控制策略的特征值对比,静止无功发生器和风机均半策略的稳定性居中。在无功恒定的前提下,稳定极限随着有功出力的增多先上升后下降,风电场系统在0.35倍额定有功时最为稳定。在有功恒定的前提下,从进相运行到滞相运行变化时,系统稳定性变弱。
3.4 系统参数对稳定性的影响
风电场接入系统的强度对于风电场的稳定有着重要影响。为讨论该参数对风电场系统稳定性的影响,设置系统短路阻抗在0.13p.u.、0.2p.u.和0.1p.u.,无功策略设置为静止无功发生器和风机均半策略,设置有功发生0.05p.u.阶跃激励,记录不同系统短路阻抗参数下的高压母线电压响应如图7所示。
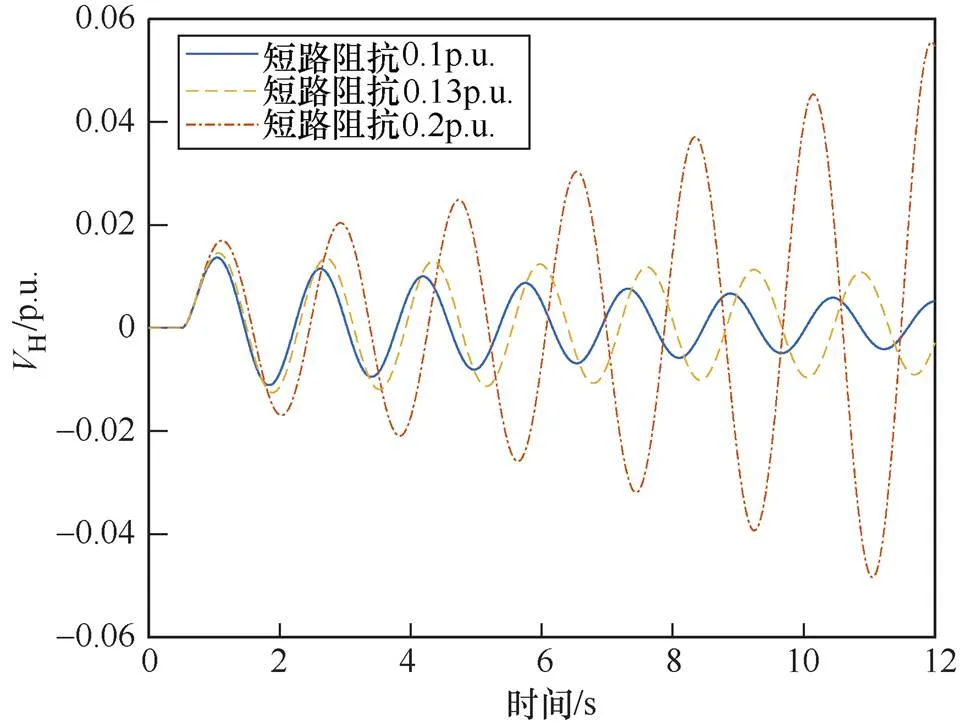
图7 不同系统短路阻抗下的高压母线电压响应
从图7可以看出,系统的短路阻抗越大,即系统网架越弱,阶跃激励后的振荡越强烈。在0.2p.u.下系统在阶跃激励下已经失稳,而在0.1p.u.时系统保持稳定,在12s波动后振荡逐渐恢复稳态。
4 结论
本文研究了风电场自动电压控制模式下无功分配的问题,得出以下结论:
1)三种不同的无功分配模式均能保证风电场稳定运行。
2)三种模式下,静止无功发生器优先策略稳定性最好,对半策略次之,风机优先策略最差,实际运行时可以考虑静止无功发生器优先的控制模式。
下一步,需进一步研究不同汇集线距离和风机地理距离对风力发电场稳定性的影响。
[1] 孙惠, 翟海保, 吴鑫. 源网荷储多元协调控制系统的研究及应用[J]. 电工技术学报, 2021, 36(15): 3264- 3271.
[2] 汪伟, 黄太贵, 王松, 等. 电网调控云平台设计与实现[J]. 电气技术, 2020, 21(12): 92-96, 101.
[3] 朱宏毅, 沈渭程, 董开松, 等. 风电机组高电压穿越技术研究及现场实测[J]. 电气技术, 2020, 21(11): 46-49.
[4] 刘华志, 李永刚, 王优胤, 等. 无功电压优化对新能源消纳的影响[J]. 电工技术学报, 2019, 34(增刊2): 646-653.
[5] 徐峰达, 郭庆来, 孙宏斌, 等. 基于模型预测控制理论的风电场自动电压控制[J]. 电力系统自动化, 2015, 39(7): 59-67.
[6] 于汀, 蒲天骄, 刘广一, 等. 含大规模风电的电网AVC研究与应用[J]. 电力自动化设备, 2015, 35(10): 81-86.
[7] 于海洋, 由楚, 李彦吉. 基于双电压控制子系统的风电场自动电压快速控制系统[J]. 电气技术, 2016, 17(9): 30-33.
[8] 刘永丽, 唐建宇, 曹洋, 等. SVC装置在风电并网中的应用及其自动电压控制[J]. 大功率变流技术, 2016(2): 62-66.
[9] 刘彦峰, 刘宏兵, 魏艳琴. 浅析风电AGC有功控制及AVC电压无功控制应用的优缺点[C]//2020年电网节能与电能质量技术论文集, 2020.
[10] 拜润卿, 宋磊, 郑伟, 等. 10GW级风电基地SVG控制参数优化研究[J]. 电力电子技术, 2012, 46(9): 13-15.
[11] 李治艳. 双馈风力发电机降阶模型研究[D]. 北京: 华北电力大学, 2014.
[12] CUI Hantao, LI Fangxing, TOMSOVIC K. Hybrid symbolic-numeric framework for power system modeling and analysis[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1373-1384.
Research on reactive power distribution of wind turbine and static var generator in automatic voltage control of wind farm
ZHU Jianhua1HE Zhuolin1YAN Weijun2JIANG Jichen3YANG Haifeng4
(1. Rundian Energy Science and Technology Co., Ltd, Zhengzhou 450000;2. Tekes County Power Supply Company, State Grid Yili Yihe Power Supply Co., Ltd, Tekes, Xinjiang 835599;3. China Resources New Energy (Tanghe) Co., Ltd, Tanghe, He’nan 473400;4. China Resources New Energy (Linying) Co., Ltd, Linying, He’nan 462600)
At present, there is a lack of in-depth analysis on the automatic voltage control (AVC) strategy of wind farm, which plays an important role in improving the voltage stability of wind farm. On the basis of considering the existing reactive power distribution mode of automatic voltage control, the small signal model with static var generator (SVG) and wind turbine is adopted to analyze the influence of AVC system on the stability of wind farm. This method takes into account the influence of reactive power distribution mode on dynamic stability in automatic voltage control system, and has good guidance for actual production. The effectiveness of the method is verified by an example of a real wind turbine.
automatic voltage control (AVC); static var generator (SVG); wind turbine; reactive power distribution
2021-09-29
2021-11-10
朱建华(1986—),男,河南洛阳人,硕士,高级工程师,主要从事电力系统分析和仿真工作。

