一种改进的SIR网络谣言传播预警模型研究

侯学慧，冯玉花

(新疆警察学院 信息安全工程系，乌鲁木齐 830001)

0 引言

网络谣言是人们为了实现某一目的或者引起社会关注，通过网络介质(社交平台、网络论坛、微博等)散播未经证实的公众难辨真伪的闲话、传闻或舆论[1]。网络谣言的广泛传播会扰乱社会秩序，甚至影响社会稳定。因此，研究者有必要发现社交网络中网络谣言的传播规律，建立符合实际情况的网络谣言传播模型，了解网络谣言传播的动力学过程[2-3]，并发现其传播过程的影响因素，提供有效的网络谣言传播预测模型、算法及决策依据，以便更好地引导和控制网络谣言的传播走势，有效控制网络舆情的发酵[4-5]。

1 基于传染病模型的网络谣言传播

根据网络谣言传播的特征，研究者发现它与传染病模型非常相似[6]。本文首先按照网络谣言的传播规律建立模型，逐步深入研究；然后对网络谣言的案例数据进行挖掘和分析，将时间轴按照每天(或每小时)为单位划分，绘出相应的真实数据散点图，建立改进的传染病SIR模型；再通过Matlab软件进行非线性参数拟合，得到与网络谣言传播的动态演化最贴近的连续曲线的分段函数，并得到预测的函数表达式，分析其演化特征；最后利用最小二乘法，计算决定系数R2，分析拟合模型的预测值与真实值之间的相关性，对网络谣言传播预测模型进行评估。

1.1 模型一：基于改进的SIR网络谣言传播模型

假设在网络谣言的传播过程中，网络中的活跃网民总数为N(N是个变量，取决于某一时刻网络中的活跃网民总数)。本文将活跃网民群体分为两类人群：一类是相信谣言的传播者I类，另一类是不信谣言的易感染者S类。设在t时刻，网络中信谣传播者I类人群占总数N的比例为I(t)，不信谣的S类易感染人群占总数N的比例为S(t)，则有：I(t)+S(t)=1。根据现实的网络谣言传播情况，当网络中的谣言传播者达到最高值时，在谣言传播群体中会产生淡忘者R类人群，即由于一些正面的辟谣措施等，使得谣言传播者不再相信谣言，从而不再传播谣言，从I类转化为S类。网络中群体分布示意图如图1所示。

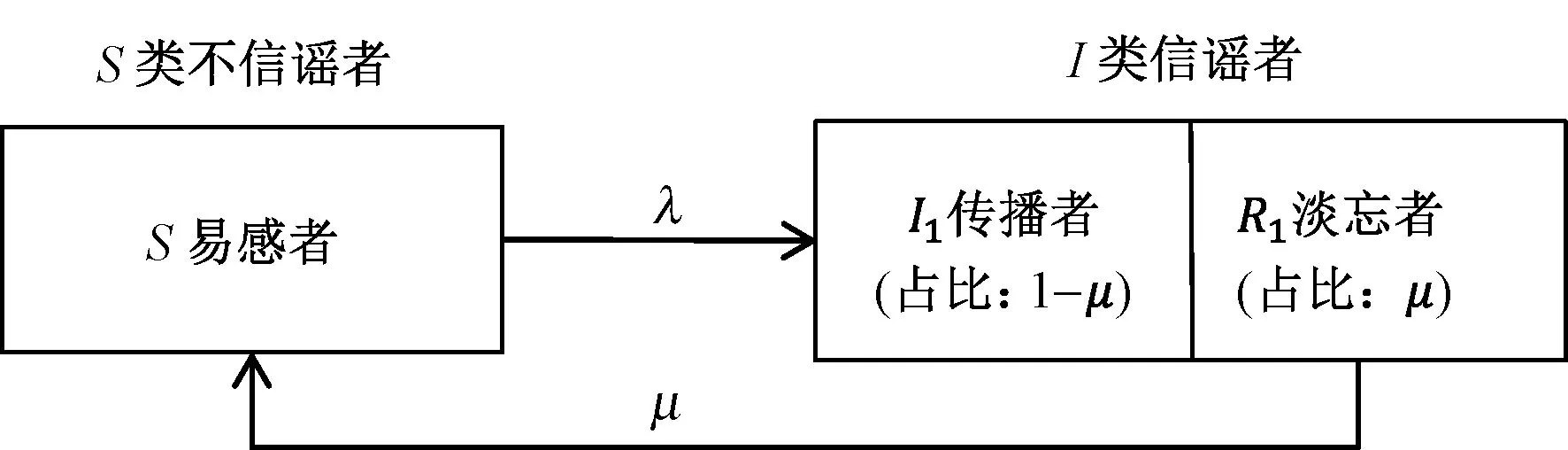
图1 网络中信谣与不信谣群体分布(SIR模型)Fig.1 Distribution of Groups Who Believe in Rumors and Groups Who Don't Believe in Rumors in the Network(SIR Model)

假设在单位时间内，每个谣言传播者接触易感者S群体可有效传播的人数为λ。μ为淡忘率(0<μ<1)，即单位时间内谣言淡忘者占信谣群体的比例。在改进的SIR模型中，淡忘者R类来自I类，R1类淡忘者进入S类不信谣人群，有效的传播则来自I1类传播者，其占比为1-μ。则在t到t+Δt时刻内，网络谣言传播者的人数增加量为

I(t+Δt)×N-I(t)×N=(1-μ)×I(t)×

λ×N×S(t)×Δt-μ×I(t)×N×Δt。

(1)

由式(1)可得

(1-μ)×I(t)×λ×(1-I(t))-μ×I(t) 。

(2)

假设在t=t0时，网络中的谣言传播者人数占比为I(t0)=I0，解微分方程式

(3)

根据伯努利微分方程的通解公式，解得

(4)

其中，n=λ×(1-μ);m=λ-λ×μ-μ。

由I(t0)=I0可以求解出C0，网络中t时刻谣言传播者的函数表达式为

(5)

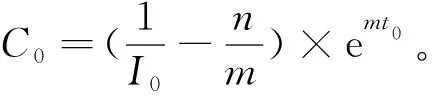
式(5)表明，网络谣言传播者I(t)×N的函数模型为Logistic模型，图像呈现S曲线型。

若网络谣言按自然规律传播，在无其他因素干扰的情况下，谣言传播将在很短时间内到达最高值，可假设在这段时间内网络中并没有淡忘者，或者R在I中的比例μ非常小，谣言传播随时间的变化呈现上升趋势；当网络中的淡忘者逐渐增多，R在I中的比例μ逐渐增大，谣言传播随时间的变化呈现下降趋势。考虑到传播率λ与淡忘率μ之间的关系，我们将网络谣言传播模型视为这两种情况的分段函数，在谣言传播过程中，无论是上升阶段还是下降阶段，均遵循改进的SIR模型。

1)网络谣言传播量上升阶段(m>0)

情形1：μ=0,m>0,m=λ。

当谣言开始散布时，网络中群体分布如图2所示。

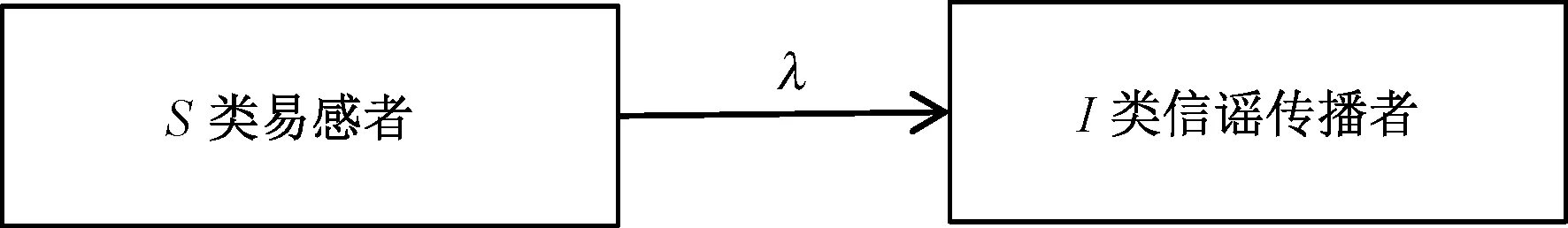
图2 网络中信谣与不信谣群体分布(SI模型初始时)Fig.2 Distribution of Groups Who Believe in Rumors and Groups Who Don't Believe in Rumors in the Network (Initial Stage of SI Model)

当网络中不存在淡忘者或者淡忘者数量很小时，则μ趋近于0；根据谣言传播量表达式 (5)，假设μ=0，得到谣言传播量上升期的函数表达式为

(6)

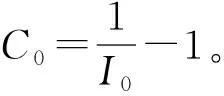
因此，网络中t时刻谣言传播量随时间变化的函数为

(7)

式(7)表明，网络谣言传播量表达式完全符合传染病SI模型[6]。在谣言传播初期，网络中不存在淡忘者，谣言的传播速度非常快，即使出现淡忘者，人数也非常小，这种情况就是μ趋近于0时的极限情况。根据与真实数据的拟合结果显示，网络谣言传播上升期的函数图像非常符合传染病SI模型。

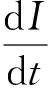
根据Logistics非线性回归方程的图像特征，我们可以预测出谣言传播量的最大值，以及达到最大值的时间周期，为建立正确的网络谣言传播预警应对机制，提供有效的数据保障和支持。

情形2：μ>0,m>0,m=λ-λ×μ-μ。

在实际问题中，相关部门可采取有效手段抑制谣言传播，如可以通过控制传播率λ与淡忘率μ，降低谣言传播量的最大值，以及缩短达到最大值的时间。

2)网络谣言传播量下降阶段(m<0)

情形3：μ>0,m<0,m=λ-λ×μ-μ。

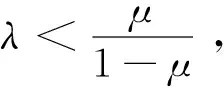
情形3适用于网络谣言传播量处于下降和消减阶段，即在谣言传播过程中，谣言发酵达到最大值后，由于淡忘者的不断增加，导致网络谣言传播量下降，直至消亡。

根据本文分析得出的Logistics函数表达式(5)，可以对网络谣言真实案例的传播数据做非线性参数拟合，从而得到网络谣言传播量随时间变化的预测值。网络谣言传播的整个过程，可以看作是改进的SIR模型中情形1和情形3交替变换的分段函数，谣言传播量不断上升的过程遵循情形1或情形2。拐点又称反曲点，指改变曲线向上或向下方向的点，即连续曲线的凹弧与凸弧的分界点。传播量在拐点后下降、消减直至消亡的过程遵循情形3，这也解释了谣言的形成、高潮、消减和消亡的4个阶段。谣言的传播是不断波动的，主要由事件发展过程中的民众主观态度、政府机关的有效干预和监管以及案件转折等众多因素决定，因此这是一个分段函数，要根据具体变化情况，调整相应的影响参数λ和μ等，而不能用某一确定的单一函数表达式来做拟合。

1.2 模型二：基于SR2IR1网络谣言传播模型

在网络谣言传播中，将活跃网民N划分为信谣群体I和不信谣群体S。在不信谣群体S中，不是所有人都是易感人群，而是存在免疫人群R2类[7]，即由于知识结构、个人素质及工作环境等原因，使部分网民已明确知晓网络谣言的虚假性，从而选择不信谣，因此网络中群体分布示意图如图3所示。

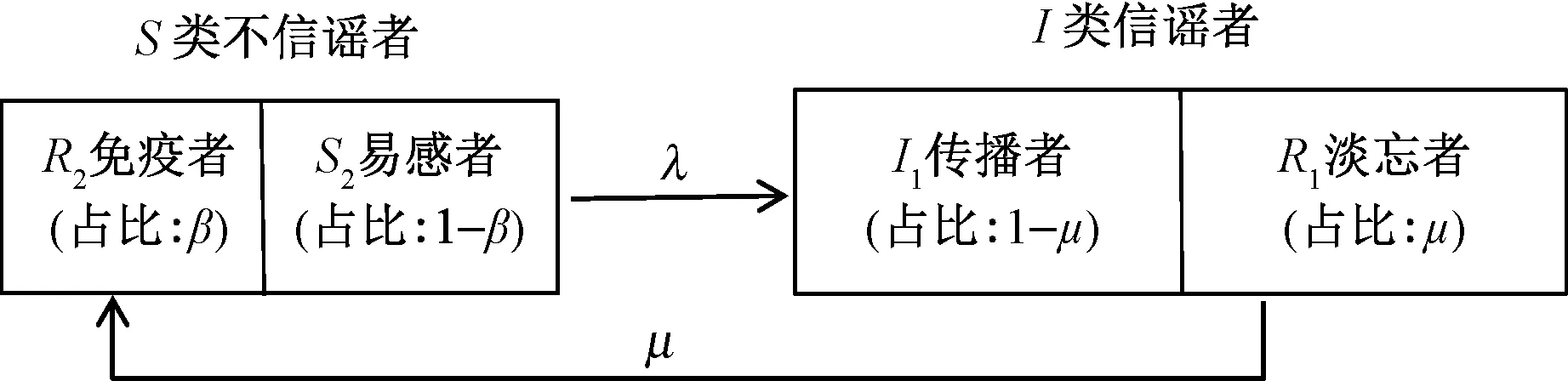
图3 网络中信谣与不信谣群体分布(SR2IR1模型)Fig.3 Distribution of Groups Who Believe in Rumors and Groups Who Don't Believe in Rumors in the Network (SR2IR1 Model)

假设β(0<β<1)为单位时间内谣言免疫者占不信谣群体的比例。R2的组成包括两部分：一是初始状态时S内的免疫人群，二是I类信谣者中淡忘人群R1的加入，使得免疫人群不断增加，直至达到网民总数，即网络谣言的消亡状态。

在改进的SR2IR1模型中，仍有I(t)+S(t)=1。免疫者R类来自S类和I类的转化，R1淡忘者进入S类不信谣人群，有效的传播则来自I1传播者，其占比为1-μ，可感染的范围是S2类易感人群，其占比为1-β。在t到t+Δt时刻内，网络谣言传播者的人数增加量为

I(t+Δt)×N-I(t)×N=(1-μ)×I(t)×λ×

N×(1-β)×S(t)×Δt-μ×I(t)×N×Δt。

(8)

假设在t=t0时，网络中的谣言传播者占比为I(t0)=I0，解微分方程式

λ×(1-μ)×(1-β)×I2。

(9)

根据伯努利微分方程的通解公式，解得网络谣言传播量随时间t变化的函数表达式为

(10)

网络中不信谣S类人群随时间变化的函数表达式为

(11)

除了参数发生改变之外，表达式的形式保持不变，与模型一中的式 (5)一致。根据参数的大小关系，网络谣言在上升阶段遵循SI模型(情形1)，在下降阶段，遵循改进的SIR模型(情形3)。

2 数据仿真

2.1 案件一

2.1.1案件背景

某地曾发生的“抢购食盐”网络谣言，在部分门户网站和搜索引擎上传播，其中，腾讯微博的转载量如图4所示。

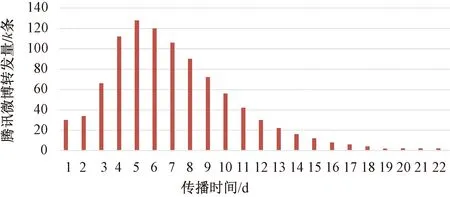
图4 “抢购食盐”网络谣言的腾讯微博转载量Fig.4 The Number of Reposts about the Case of Rush-to-buy-salt Network Rumors on Tencent Weibo

2.1.2数值模拟及结果分析

本文使用Matlab软件对建立的数学模型进行仿真实验，根据网络谣言真实案例的传播量数据，进行非线性参数拟合，得到与网络谣言传播的动态演化最贴近的连续曲线的分段函数，建立合理的数学模型，分析其演化特征。

网络谣言传播在上升阶段遵循SI模型，到达拐点后，下降阶段遵循改进的SIR模型。利用Matlab软件，根据真实数据非线性回归拟合得到Logistic模型函数表达式，即从谣言传播开始的第1～22 d，设网络中t时刻谣言传播者的人数为y(t)，则非线性参数拟合方程为

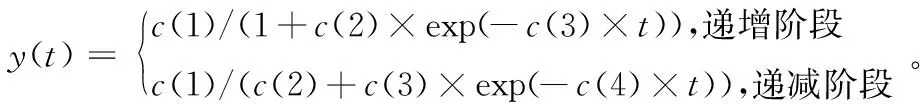
(12)

网络谣言传播上升阶段遵循SI函数模型，函数表达式如式(7)所示，由图4的初始数据，计算初始量C0，用非线性参数拟合网络谣言传播量上升阶段的预测函数表达式为

(13)

由此得到，y预测最大值=165 074，y真实最大值=127 924。

网络谣言传播下降阶段遵循改进的SIR函数模型，函数表达式如式(5)所示，由图4当中的第5～22 d的数据，计算初始量C0，用非线性参数拟合网络谣言传播量下降阶段的预测函数表达式为

(14)

由此得到，y预测最大值=151 490，y真实最大值=127 924。

综上所述，在网络谣言从形成、扩散，逐步到达高峰直至消减的传播过程(1≤t≤22)中，谣言传播量I(t)×N随时间变化的拟合预测函数图像如图5所示。

图5 “抢购食盐”网络谣言传播的拟合函数示意图Fig.5 Fitting Function Image of Transmission of Rush-to-buy-salt Network Rumors

对模型进行非线性函数拟合后，须评价回归模型的拟合优度。根据决定系数的计算公式，利用Matlab软件进行求解，得到实际值与预测值之间的差异为

(15)

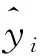
因为S(t)×N=N-I(t)×N，由此我们也可以得到网络中不信谣人群随时间变化的预测函数图像，如图6所示。Smin=21 589，说明在不信谣S类群体中，存在免疫群体R的人数至少是21 589人。

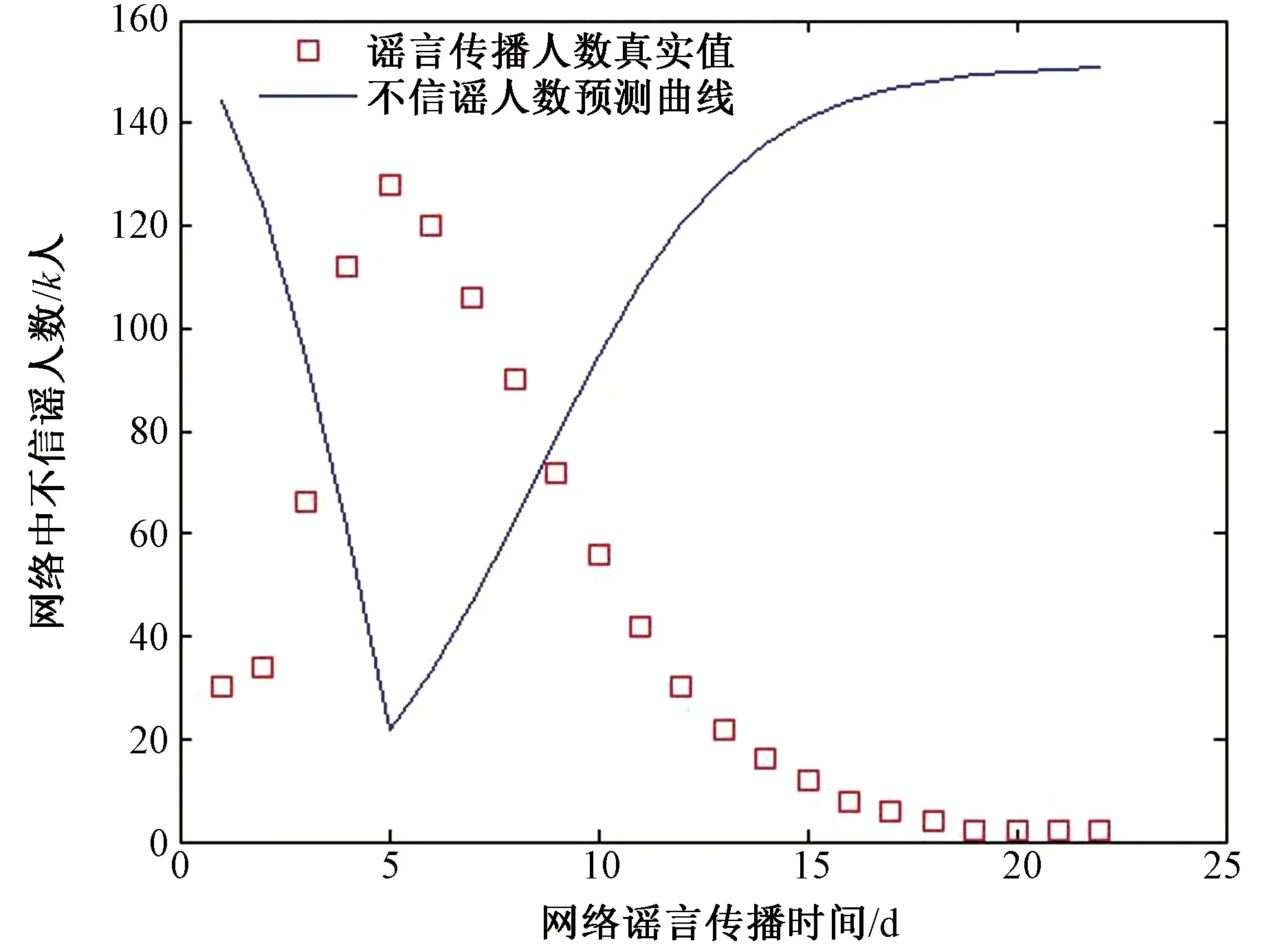
图6 “抢购食盐”网络传播中不信谣人群的拟合函数示意图Fig.6 Fitting Function Diagram of People Who Do not Believe in the Rumors in the Transmission of Rush-to-buy-salt Network Rumors

2.2 案件二

2.2.1案件背景

某知名演员在经济合约纠纷案中，其个人银行账户流水未经本人授权被提供给第三方，个人信息被侵犯，该事件引发舆论关注。在大数据环境下，通过舆情监测平台得到一周之内各新闻网站和大型媒体对该舆情的传播情况，如图7所示。

图7 舆情传播量随时间变化图Fig.7 Image of Transmission of Network Public Opinion over Time

2.2.2数值模拟及结果分析

由于分析方法类似，本文只模拟了两次舆情高峰及下降过程，即在0～55时，设网络中t时刻舆情传播者的人数为y(t)，非线性拟合方程为

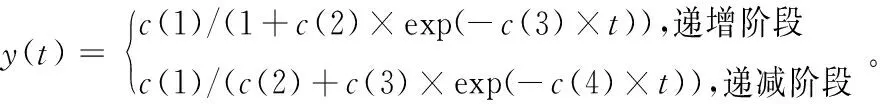
(16)

对于第一波递增，根据SI函数模型，计算得到拟合预测函数为

(17)

由此得到，y预测最大值=15 354，y真实最大值=13 800。

对于第一波递减，根据SIR函数模型，计算得到拟合预测函数为

(18)

网络舆情传播的预测值是分段函数，舆情从形成、扩散、第一次到达高峰直至消减(0≤t≤30)的函数图像包括两部分，分别如图8和图9所示。

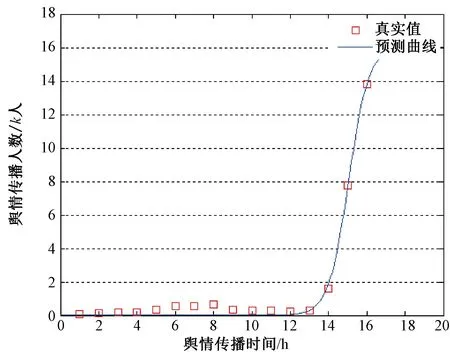
图8 第一波舆情上升图像(基于SI模型)Fig.8 The First Stage of Public Opinion Rising (Based on SI Model)

图9 第一波舆情下降图像(基于SIR模型)Fig.9 The First Stage of Public Opinion Declining (Based on SIR Model)

对于第二波递增，根据SI函数模型，计算得到拟合预测函数为

(19)

由此得到，y预测最大值=25 712，y真实最大值=16 479。

对于第二波递减，根据SIR函数模型，计算得到拟合预测函数为

(20)

网络舆情传播从第二次扩散到达高峰值，直至消减(30≤t≤54)的函数图像同样包括两部分，分别如图10和图11所示。

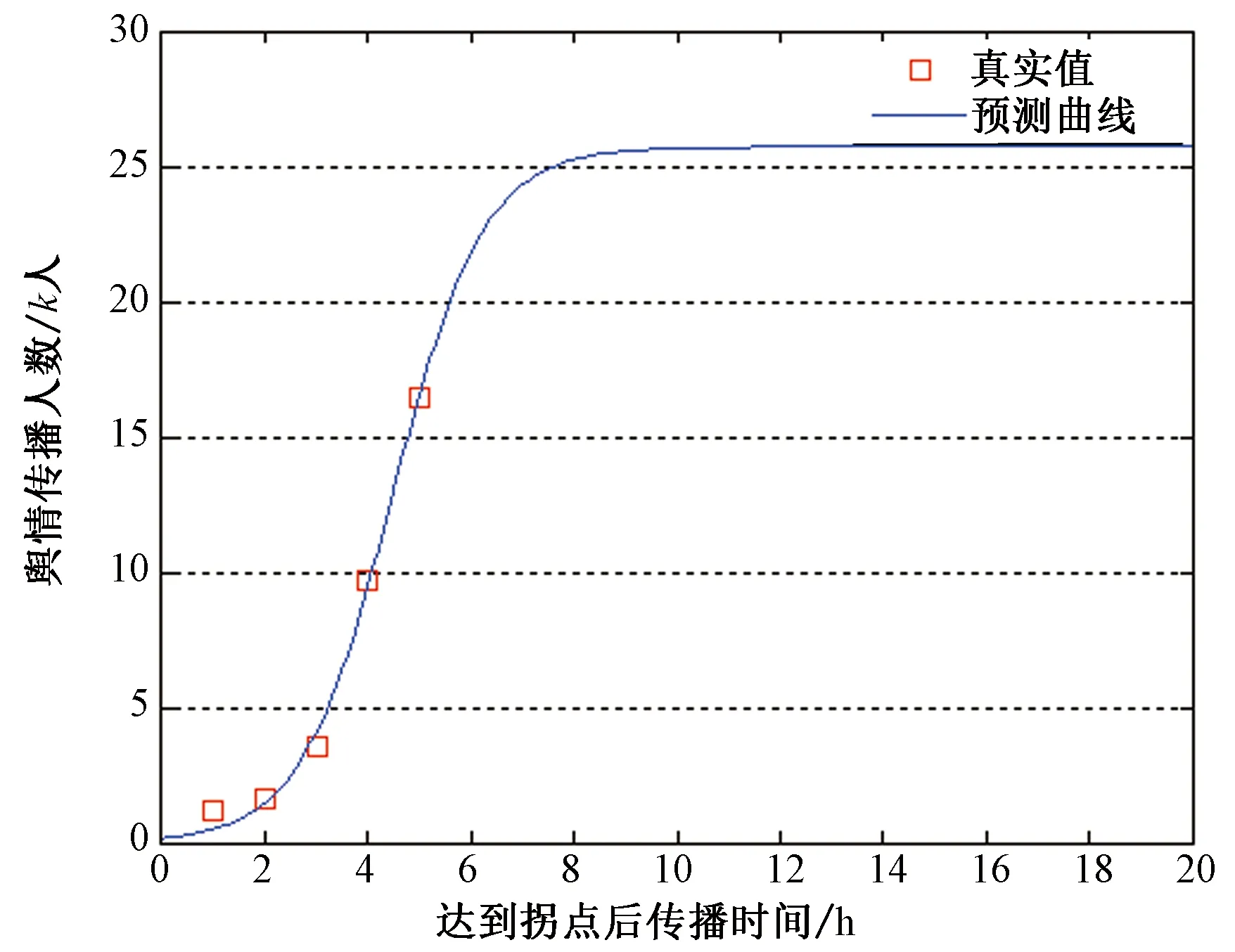
图10 第二波舆情上升图像(基于SI模型)Fig.10 The Second Stage of Public Opinion Rising (Based on SI Model)

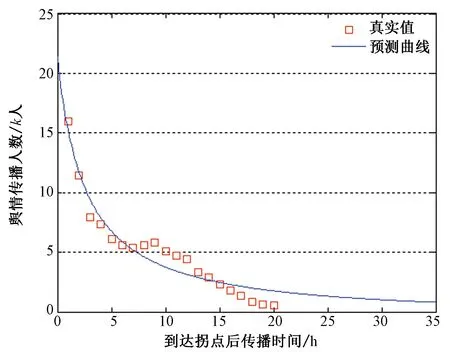
图11 第二波舆情下降图像(基于SIR模型)Fig.11 The Second Stage of Public Opinion Declining (Based on SIR Model)

通过分析0～54时刻舆情传播随时间的变化情况，可以预测舆情每一次上升可能到达的最高值，并预测舆情传播周期，为控制和引导网络舆情提供数据支持。舆情传播从形成、扩散，到达高峰直至消减(0≤t≤54)的函数图像，如图12所示。

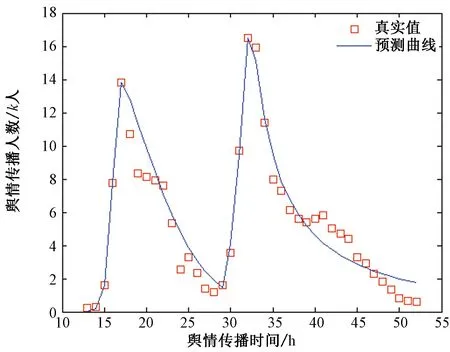
图12 舆情传播过程随时间拟合的函数图像Fig.12 Fitting Function Image of Public Opinion Transmission over Time

对模型进行非线性函数拟合后，须评价回归模型的拟合优度。经计算得出，此分段函数的残差R2=0.936 9，说明用此模型拟合效果较好。

3 结束语

网络谣言传播是遵循规律性变化的。网络谣言传播在上升阶段时，由于在很短时间内就能达到高峰值，假设信谣I类群体中不产生R类淡忘群体，那么谣言传播遵循传染病SI模型，该模型的图像呈现S型曲线特征。我们从每一次谣言上升开始的前几个小时就能分析出可能达到的高峰值和发酵周期，从而可及时采取有效措施，控制和引导谣言走势。由于网络中民众的主观态度、政府采取的有效手段、客观事件的影响力等随谣言传播的时间而发生变化，所以整个谣言传播过程是分段函数。谣言传播在下降阶段时，在谣言传播I群体中产生了淡忘者，遵循改进的SIR模型，我们利用Matlab软件对真实数据做非线性参数拟合，得到该模型的图像呈下降趋势，直至谣言消亡。以此可得到谣言传播量随时间变化的预测函数，为建立网络谣言传播预警和导控机制提供了数据预测和量化支持。