基于城市遥感卫星影像对的立体匹配

赵 杰，陈小梅*，侯玮旻，韩嘉威

（1.北京理工大学 光电学院，北京100081；2.北京理工大学 光电成像技术与系统教育部重点实验室，北京100081）

1 引 言

城市三维重建对于城市规划、智慧城市构建具有非常重要的意义，三维重建的核心技术是立体匹配［1］。研究人员提出了大量的立体匹配算法，其4个步骤主要包括：（1）匹配代价计算；（2）代价聚合；（3）视差计算；（4）视差细化［2］。

在匹配代价计算中，学者们提出了绝对值差之和（Sum of Absolute differences，SAD）、平方差之和（Sum of Squared differences，SSD）、归一化互相关系数（Normalized Cross Correlation，NCC）、基于互信息的匹配代价计算方法以及基于Census变换的匹配代价计算方法等。其中，基于Census变换的匹配代价计算方法由于它对于光照度变化不敏感以及计算效率高得到了广泛的使用［3-4］。但是Census算法对于噪声非常敏感且在弱纹理区域匹配精度不足，城市卫星遥感影像上存在大量的噪声以及弱纹理区域，因此该算法对于城市区域卫星遥感影像无法取得非常好的效果［4］。

根据代价聚合方法的不同，立体匹配算法可分为局部立体匹配算法与全局立体匹配算法［2］。局部立体匹配算法通过设定一邻域窗口的形式，利用像素局部的信息来表征当前像素的匹配特征，增加了可靠性与稳定性。全局立体匹配算法在进行像素点匹配时利用了图像的所有信息，因此在处理具有噪声、重复纹理以及遮挡现象的图像时表现更为出色［5］。不过，全局立体匹配算法的计算效率低于局部立体匹配算法［6］。2008年，Hirschmuller提出了半全局匹配算法（Semi-Global Matching，SGM）［7］，使用动态规划算法作为代价聚合的方法，通过多个在一维方向上的优化来代替二维图像整体代价优化策略，该算法兼顾了局部匹配算法的效率和全局匹配算法的效果［8］。但在以动态规划思想作为代价聚合的过程中，为保护视差的连续性，对视差不连续的区域进行了惩罚，这导致视差突变的物体边缘区域的视差值准确度下降［9］。对于视差细化部分，子像素拟合、一致性检查、唯一性约束以及剔除小连通域等方法是常用的视差优化方法，但是城市遥感影像具有大量的建筑阴影以及弱纹理的建筑屋顶，上述方法对这些较低信噪比的区域难以产生值得信赖的视差值［7］。

综上所述，本文设计了一个基于改进的Census变换的匹配代价函数，它保持了Census变换对光照变化不敏感的特性，同时具有较强的抗噪能力，对匹配点相似度的刻画更加细腻。代价聚合时，在动态规划优化方法的基础上，增强了物体边缘保护能力；在常规视差细化方法的基础上，针对城市区域卫星遥感影像中存在的大量建筑阴影、弱纹理建筑屋顶等区域导致的匹配视差不准确现象提出了针对性的细化策略。

2 基于改进Census变换的匹配代价

基于Census变换的匹配代价计算通过利用邻域像素相对于中心像素的亮度关系作为该中心像素的局部特征信息，利用汉明距离作为衡量左右两幅图像中对应像素的相似度度量［10］。Census变换的步骤为取中心像素p的一邻域M，邻域内的像素值若是大于中心像素值便记为1，否则记为0。表达式如下：

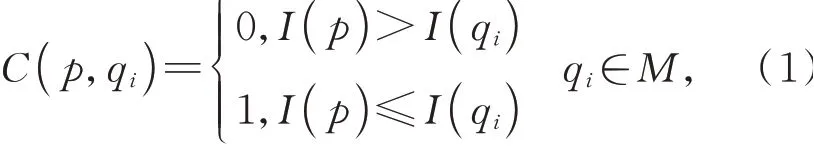
其中：C表示变换结果；p表示中心像素；qi表示邻域像素；I(p)和I(qi)分别表示对应的灰度值。

将中心像素p与邻域每一像素点进行比较得到反映p点局部特征的二进制串。通过比较左右两幅图像对应像素点的二进制串的亦或关系得到这两点的相似度，即匹配代价。

该方法简单迅速，利用相对亮度作为特征，因此对于两幅匹配图像之间的光照变化并不敏感。但是该方法只将中心点邻域像素划分为两种情况，并且划分过程过于依赖中心点像素，若中心像素灰度值因为噪声等影响发生较大变化，变换结果会产生较大的偏差［11］。例如，某一中心像素灰度值略大于所有邻域像素的灰度值，因此变换后的二进制串结果应是一串0，若噪声使得中心像素灰度值小于邻域像素灰度值，则会得到一串1的二进制串。此外，该方法能够区分的视差层级完全局限于所取邻域的大小，若取5×5则只能分辨25个层级，不能得到非常细腻的视差值。

本文提出一种n阶加权的Census变换算法，以适应城市卫星遥感影像大量噪声及弱纹理区域的问题。n阶加权Census算法的思想依旧沿用Census变换中利用相对亮度作为特征以应对光照变化，但不再以中心像素作为标准，而是以整个邻域内亮度均值作为比较标准，利用邻域内像素灰度值的最大值、最小值以及设置的n个阈值将整个邻域划分为n个状态。计算方法如下：

其中：Imin与Imax分别代表p点邻域像素内的最小灰度值与最大灰度值；n代表n个状态；Ith1，Ith2，Ith(n-1)分别代表第1个阈值、第2个阈值以及第n-1个阈值。

由于整个邻域像素被划分为n种状态，所获得的匹配代价比两匹配点的相似性度量更加细腻。

基于越靠近中心像素，越能代表中心像素局部信息特征的事实，对n阶Census变换得到的数串进行相似度度量时，加入距离权重信息。两匹配像素在分别经过n阶Census变换之后得到两数串，两数串内对应数值之差的和越小，两像素越相似，因此定义以n阶加权Census变换为基础的匹配代价计算为：

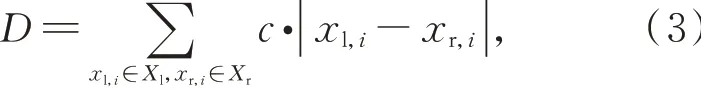
其中：Xl为左图像素p点经n阶Census变换之后的数串，Xr为右图匹配点经n阶Census变换之后的数串，xl，i与xr，i分别为Xl与Xr内一数值，c为对应邻域像素与p点之间的距离。

3 边缘引导优化的匹配代价聚合

匹配代价计算通常使用邻域像素的灰度信息来计算两像素之间的匹配程度，这很容易受到图像噪声、弱纹理或重复纹理等因素的影响［12］。代价聚合则是通过建立像素之间的联系，以一定的准则，例如相邻像素应该具有连续的视差值，来优化第一步得到的匹配代价矩阵，使匹配代价值能够准确地反映像素之间的相关性。SGM算法［7］采用在多个一维方向的优化代替在二维图像整体进行优化的思想，兼顾了局部匹配算法的效率和全局匹配算法的效果，因此得到了广泛的应用［13-14］。

SGM算法的匹配代价聚合方法通过动态规划优化的能量函数为：

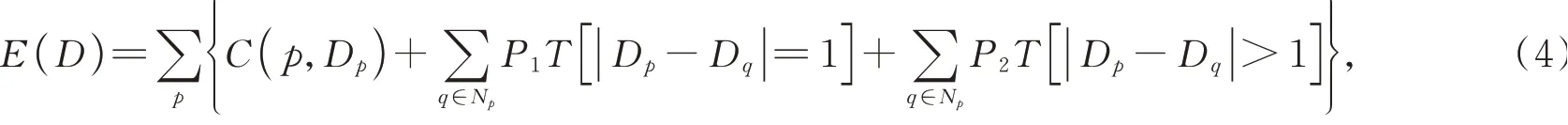
其中：第一项为视差为D的所有像素的匹配代价之和；第二项表示对于像素p邻域N p内的所有像素q，若其视差相对于p点视差变化为1，则加一惩罚值P1，第三项表示对于像素p邻域N p内的所有像素q，若其视差相对于p点视差变化大于1，则加一惩罚值P2。

该能量函数基于这样一个假设，即某像素邻域内的视差值应与该像素视差值相等或相差很小，因此对于视差变化较大的区域加一较大的惩罚项P2。当一个匹配使得所有匹配点对应的匹配代价和最小时，得到最优匹配。但是城市区域遥感影像包含大量的建筑分布，因此存在视差变化较大的区域，若通过式（4）优化则建筑边缘处的匹配效果较差。

若能够提前知道图像中视差变化较大的位置，则可以对这些位置设置一个较小的P2惩罚值，从而解决视差变化区域难以得到较小匹配代价问题。视差变化较大的区域一般发生在建筑屋顶的边缘位置。图像的梯度信息一定程度上体现了图像的边缘信息，梯度较大的位置较有可能位于物体边缘位置，因此可以通过求解图像梯度的方法获得建筑的边缘，进而根据梯度幅值设置合理的P2惩罚值。P2的取值原则如下：

其中：P2c为大视差惩罚值，g为该像素位置处的梯度幅值，P1为式（4）中的惩罚值。

4 基于场景的视差优化

视差细化时，通常使用子像素拟合的方法使当前获得的整像素级视差精度提高到子像素精度，使用一致性检测和唯一性约束来提高匹配结果的置信度，通过剔除小连通域来减小错误视差区域［7］。对于大多数场景，这些方法能够达到较好的视差细化效果，但是由于城市区域卫星遥感影像存在大量的建筑阴影和建筑屋顶的弱纹理，上述方法无法在阴影区域取得准确的视差，并获得建筑屋顶的完整视差。因此，针对城市区域需要进行阴影去除和提高屋顶视差的完整度。

4.1 阴影检测及去除算法

建筑阴影区域的信噪比非常低，几乎无法获得有助于匹配的信息。阴影与非阴影的边缘区域因为像素亮度变化大，容易被认为是视差不连续区域，从而导致误匹配。因此，通过检测图像中的阴影区域，进而对视差图中阴影区域进行处理可减小阴影带来的影响。

本文采用双峰阴影检测法。城市卫星遥感影像的直方图具有明显的双峰现象，如图1所示，其中小于峰谷的像素值可认为是场景中的阴影区域［15-16］。双峰法阴影检测结果如图2所示。

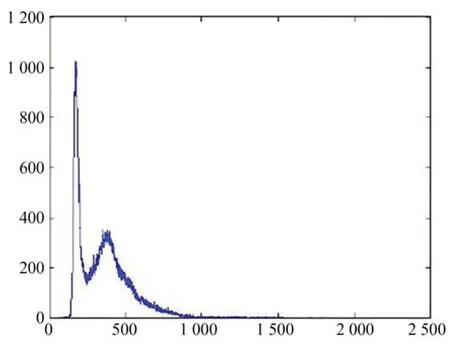
图1 城市卫星遥感影像直方图Fig.1 Histogram of urban satellite remote sensing image

图2 双峰法阴影检测结果Fig.2 Shadow detection result of double peak method

阴影一般是由太阳光照射到建筑表面投影到地面或者较低的建筑屋顶造成的，因此阴影区域的视差值应与其邻域内高程值较小的视差值相同。本文使用阴影周围其他像素点的视差信息对阴影区域视差值进行合理推断，并进行填充修正。阴影区域视差值修正填充流程如下：

（1）获取阴影区域周围邻域像素。首先，基于形态学的方法对检测到的阴影连通域进行膨胀操作；然后，使用膨胀之后的阴影连通域减去原始阴影连通域，由此得到阴影区域周围邻域像素M。计算公式如下：

其中：A为阴影连通域，B为3×3矩阵模板，⊕为形态学膨胀操作，M为阴影区域周围邻域像素。

（2）分析统计阴影邻域区域像素的视差数值。由式（1）获得M阴影邻域统计视差信息相同的相邻像素的个数，其中具有相同视差的连续像素点个数占比超过一定阈值ε（本文设置为0.25），且高程信息较小的高程值即是合理的阴影区域填充视差值。图3为阴影邻域区域视差示意图。图4为去除阴影影响的图像，由此可以看出该步骤对减小阴影影响具有非常好的效果。

图3 阴影邻域区域视差示意图Fig.3 Disparity diagram of shaded neighborhood area

图4 阴影区域视差修正结果Fig.4 Results of disparity correction in shadow area

4.2 基于建筑区域提取的建筑屋顶视差优化

由于城市内建筑物屋顶大多为弱纹理区域，该区域像素值变化不大，可提供给立体匹配算法的可用信息较少，造成视差图中屋顶区域存在一些空洞，并且邻域内视差分布不平整。这种情形下，可采用基于区域生长的分割算法。由于建筑屋顶大多为矩形，因此在分割算法中辅以直线段检测算法，进一步分割边缘位置，得到较为精确的建筑屋顶分割区域。城市中大多数的建筑屋顶都是水平平面，同一建筑屋顶具有相同的高程，也即拥有相同的视差。因此，以区域分割辅以直线段检测的方法得到建筑屋顶区域；平均建筑屋顶区域视差得到平整的屋顶视差［17］。分割算法可以准确地检测建筑屋顶区域，得到完整的建筑屋顶视差。

基于区域分割，辅以直线段检测的建筑屋顶分割算法和建筑区域视差平整算法分别用伪代码Algorithm 1，Algorithm 2表示，如图5所示。

图5 算法伪代码Fig.5 Algorithm pseudocode

5 实验及分析

本文提出的立体匹配算法以基于n阶Census变换的匹配代价为代价计算方法，以保留物体边缘信息动态规划方法为代价聚合，并以WTA策略作为代价计算方法，同时针对城市阴影以及建筑屋顶进行视差优化。首先在Middle-Bury实验数据集上对本算法的通用性及准确性进行了验证，然后在真实的城市遥感影像对上进行了实验。

5.1 算法代价计算及代价聚合改进效果的实验

MiddleBury实验数据数据集是2001年Schaestein等为统一评价已有的各种立体匹配算法的效果而创建的数据集。该数据集包含多个场景，每个场景包含左视图和右视图，以及对应的左视差图和右视差图［2］，可以方便对算法得到的视差图与真实视差图进行比较，因此在立体匹配算法的效果评价中得到了广泛的应用。MiddleBury实验数据集可在https：//vision.middlebury.edu/stereo/data/获得。本文使用Middle-Bury实验数据数据集中多个场景对本文算法的效果进行了验证，并与网站中SGM算法的实验结果进行比较。

MiddleBury实验数据集中Piano场景的实验结果如图6所示。相较于SGM，本文提出的算法可得到更完整的物体轮廓和精准的物体边缘视差图。

图6 MiddleBury数据集Piano场景图像的实验结果Fig.6 Experimental renderings of Piano scene images in MiddleBury dataset

在MiddleBury实验数据集的网站中默认展示了各种立体匹配算法（包括SGM算法）误差大于2的像素占总像素数的百分比。因此，这里将视差误差小于2的像素认定为匹配正确，统计正确匹配像素占总像素数的比例作为准确率（acc），以反映计算所得视差和真实视差之间的差异性，计算方法如下：其中：cond Small(S，T，a，b)表示若S小于T为真，则取a，否则取b；d表示计算得到的视差；d G表示真实视差；M表示图像像素个数。

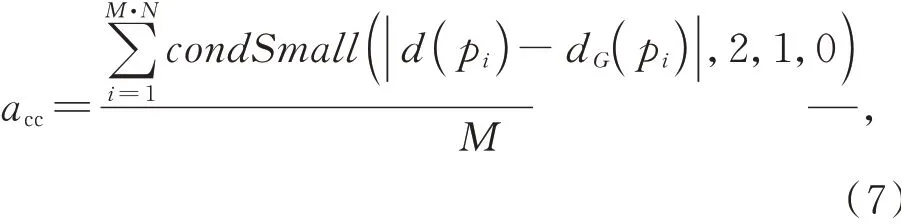
表1展示了本文算法与SGM算法在Middle-Bury实验数据多个场景下准确率的统计结果。由表1可知，在改进匹配代价函数以及代价聚合优化函数之后，本算法在多个场景下都取得了更高的准确率。在各场景下本算法的准确率平均值相较SGM算法提升了4.43%。

表1 Middlebury实验数据集上算法的准确率Tab.1 Accuracy rate of algorithms on Middlebury experimental dataset （%）

5.2 真实遥感影像实验

World View-2于2009年10月发射，是第一颗高分辨率8波段多光谱商业卫星，能够提供0.5 m分辨率的立体影像产品。为了检验该算法在城市区域卫星遥感影像对上进行立体匹配的可行性，实验使用的WorldView-2卫星遥感影像对如图7所示。

图7 World View-2国家图书馆区域遥感影像对Fig.7 WorldView-2 national library regional remote sensing image pair

为展示本文算法在应对场景亮度变化方面的效果，使用WorldView-2卫星拍摄的国家图书馆区域遥感影像对进行了实验，该场景中包含明显的亮度变化，严重影响立体匹配算法的准确性，实验结果如图8所示。

由图8可以看出，以基于n阶加权Census算法作为匹配代价函数以及保留物体边缘的代价聚合策略的立体匹配算法，可以很好地应用于城市卫星遥感影像对的立体匹配中，同时本文算法比SGM算法具有更少的误匹配点，图像边缘更细腻。

图8 WorldView-2遥感影像对上不同算法的效果图Fig.8 Algorithm renderings on WorldView-2 remote sensing image pair

为验证本文所提的在建筑屋顶区域的视差优化方法，使用与图7同一景影像中建筑密度以及复杂程度更高的场景进行了实验，实验原图如图9所示，该场景中还包含大量的阴影区域。建筑屋顶视差优化的实验结果如图10所示，可以看出，经过优化后的视差图更加平滑，建筑屋顶完整度更高。

图9 建筑屋顶视差修正实验原图Fig.9 Original images of building roof parallax in correction experiment

图10 建筑屋顶区域视差优化效果图Fig.10 Disparity optimization images of roof area of building

由于遥感影像对没有标准的Ground Truth视差图作为比较，对于城市区域遥感影像对的匹配结果只从主观视觉进行了分析。为了定量分析其效果，本文利用基于有理函数的三维重建方法，由本文算法获得的视差图10（b）计算对应的数字 高 程 模 型（Digital Elevation Model，DEM）图［18］，结果如图11所示。

由先验知识可知，城市建筑的屋顶大多为水平平面，其高程一致，因此可通过计算建筑屋顶平面的高程方差来评价算法的准确度。选取图11中不同高程、不同建筑的a，b，c 3个区域进行分析，分别计算3个区域内的高程均值以及高程方差，结果如表2所示。

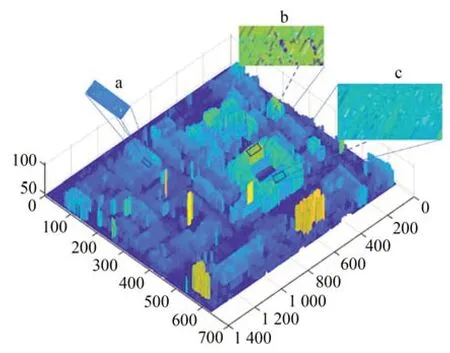
图11 基于WorldView-2卫星遥感影像视差图的DEM图Fig.11 DEM map based on disparity map of WorldView-2 satellite remote sensing image

由表2可知，a区域的高程方差为1.739 0，b区域的高程方差为0.009 8，c区域方差为0.37，3个区域的方差平均值为0.71，这表示本算法可以得到比较平整的建筑屋顶重建效果，准确性较高。

表2 建筑屋顶高程数据统计信息Tab.2 Statistical information of building roof elevation data

6 结 论

本文为解决城市遥感影像多建筑阴影以及建筑屋顶无纹理导致立体匹配效果不理想的问题，提出了适用于城市遥感影像对的立体匹配方法。首先，提出了基于改进Census变换的代价计算方法。然后，利用建筑边缘信息强化了算法在屋顶边缘处匹配的稳定性。最后，给出了建筑阴影区域以及建筑屋顶区域的视差修正方法。实验结果表明：在MiddleBury数据集上，本文算法的准确率比经典SGM算法高4.43%；在城市区域WorldView-2立体影像对上，建筑屋顶的高程方差为0.71。该方法满足基于城市卫星遥感影像对获取高精度视差图的要求，能够为城市三维重建提供良好的条件。