武汉典型城市交通因素对COVID-19传播的影响研究*

彭 然, 王竞钊, 刘业浩, 刘学良

引言

2020年COVID-19疫情肆虐全球，其最早被发现于湖北武汉，因传染能力强，全球已有数亿人被感染。现代城市因人的流动而繁荣，交通是流动的保障，但也必然成为疫情传播的桥梁，因此在疫情防控中明确城市交通对于疫情传播的影响特征十分必要。

当前部分学者已针对COVID-19进行了交通领域的研究，如Kutela等[1]对400多篇有关COVID-19的文献进行地理分布统计，发现美国、中国、日本和英国对于该类研究最多，且大部分与交通领域息息相关。多元主体网络技术、SEIR模型以及CGE模型被应用于COVID-19疫情经由城市交通的传播特征研究，并由此得出了交通管制有利于控制疫情的结论[2-5]。Jizhou Huang、Xin Li、G Matosevic等基于COVID-19感染大数据进行了定量研究并提出了相应的解决方案[6-9]。根据世界各地不同的疫情传播特征，各国学者还开展了相应的地域性研究[10-12]，如Zilin Bian等[13]以美国西雅图和纽约为例，将COVID-19大流行时期主管部门所采取的行动在交通系统中的时滞效应进行量化研究，得出当时的“居家令”和“解封政策”对城市流动性有着主导性影响力的结论，此外还发现COVID-19的大流行使城市居民尤其是贫困人群的出行风险加剧。又如Jessie Pinchoff等[14]对肯尼亚内罗毕的5个贫民窟进行了实地调查，发现贫民窟居民特别是男性居民公共交通出行时所面临的风险更高，因此认为必须采取必要的防护措施以降低人群在城市公共交通中发生感染的几率。

目前关于城市驱动因素对COVID-19传播影响的研究中，基于感染数据分析城市中商业、交通、土地利用混合度、老龄化以及容积率等因素对COVID-19疫情传播影响的研究证实了城市交通驱动因素对疫情传播产生了显著影响，但是对其影响特征还未进行深入讨论[7]。本文延续该研究，以2020年初全球首先受到COVID-19重创的武汉为例，基于空间异质性视角构建最小二乘模型（OLS, Ordinary Least Squares）和地理加权回归模型（GWR, Geographically Weighted Regression）进一步对城市各区域路网密度、道路可达性、轨道交通站点分布以及公交站点分布等4个典型交通驱动因素对于疫情传播的影响特征进行深究，以期为该类传染病防控中的交通策略制定提供参考。

1 数据来源与研究方法

1.1 研究区域概况

武汉作为华中中心城市和中国重要的综合性交通枢纽，全市常住人口约1121.2万人。武汉是全球最早通报疫情，也是中国唯一受到疫情严重冲击的特大城市，累计确诊病例超过5万例。当时人类面对未知病毒疏于防范，使得在较长时期内病毒处于自由扩散的状态，因此武汉是研究城市交通对于疫情传播影响特征的最适宜对象。

本文的研究区域为江岸、江汉、硚口、汉阳、武昌、洪山、青山等7个武汉传统中心城区（图1），去除江河、湖泊等水域后面积共计约804km2，是武汉人口分布最为密集的区域。

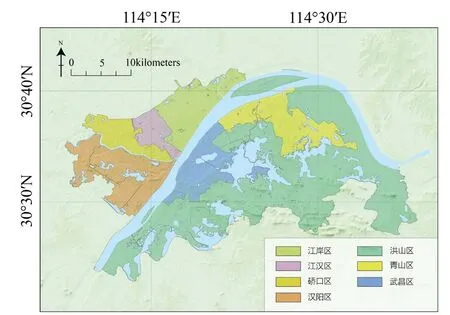
图1 武汉中心城区行政区划

1.2 数据来源

本文数据包括武汉7个中心城区的街道区划矢量数据、道路网络矢量数据、轨道交通站点POI数据以及公交站点POI数据等，此外还爬取中国疾病预防控制中心和腾讯集团联合发布的感染病例实时分布地图，汇总了截至2020年2月15日武汉市内3,397个居住区内的25,244个确诊病例数据。当时武汉已处于疫情爆发的后期，累计确诊病例达到了37,914例，占武汉2020年全年确诊人数的75.29%。本文的数据有效汇总率为66.58%，感染病例分布数据存在部分缺失主要是疫情初期武汉市部分街道和社区统计的混乱和不及时所致，但是本文已基本汇总了当时官方平台所通报的全部病例，其样本量较为充足，数据的全面性可以有效支撑本次研究。

虽然本文数据汇总的截止日期距离武汉封城以及由此导致的市内交通停摆已达到24天，但是由于疫情爆发初期检测手段的严重滞后以及COVID-19感染后存在较长的潜伏期，由此本文的研究病例绝大多数依然为2020年1月23日武汉封城前市内交通正常运行且人口自由流动状态下被感染的，其完全可以被用于分析城市正常运转状态下各类交通驱动因素对于疫情传播的影响问题。

根据武汉市确诊病例核密度分布图（图2）可知武汉高密度感染区呈块状分散分布，其中位于江汉区的华南海鲜批发市场周边感染密度最高，而该市场正是全球首先发现疫情之地。其他如光谷、徐东、沌口、钟家村、王家湾和中南路等交通便捷且人口流动性较大的城市中心地段感染密度也同样较高，整体而言当时武汉的疫情呈现出典型的社区传播状态[15]。

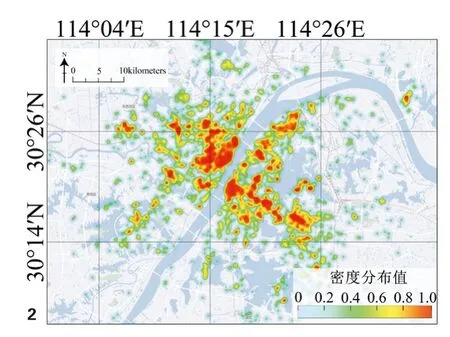
图2 武汉确诊病例核密度分布

街道作为中国基层行政单元，具有一定的功能完整性和交通一体性，因此本文将研究区域进一步细分为93个街道，该划分方式较之于常见的网格划分法能够更好保证每一个基本研究单元人口结构平衡，从而有效提高所求得数据的准确性与稳定性[8]。基于ArcGIS10.7将疫情数据进行处理，可得出反映各街道感染人数与其占地面积之比的COVID-19感染密度分布图（图3），由此可见具备更便捷交通条件的城市中心区域感染密度较之城市外围区域更高。

图3 武汉COVID-19感染密度分布

1.3 交通驱动因素的选取与处理

本文选取武汉中心城区93个街道的路网密度（图4）、道路可达性（图5）、轨道交通站点分布（图6）和公交站点分布（图7）等四个交通驱动因素作为研究变量。

图4 a 武汉城市路网核密度分布

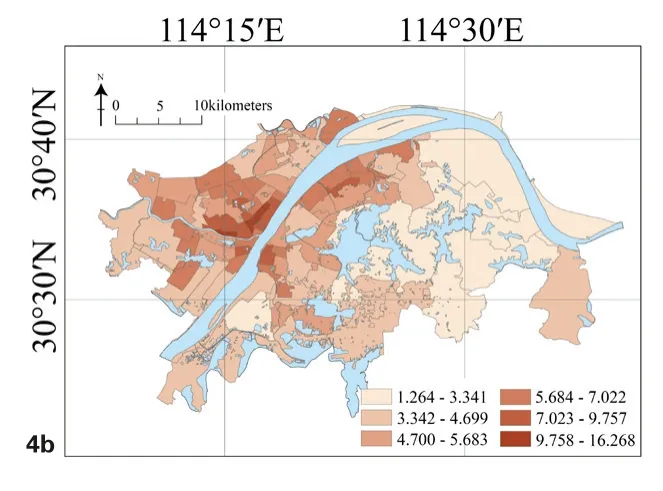
图4 b 武汉各街道路网密度Dk分布

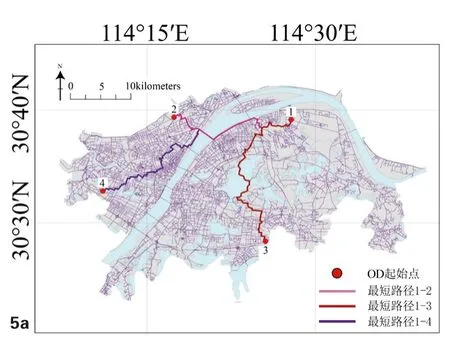
图5 a 武汉道路可达性计算示意

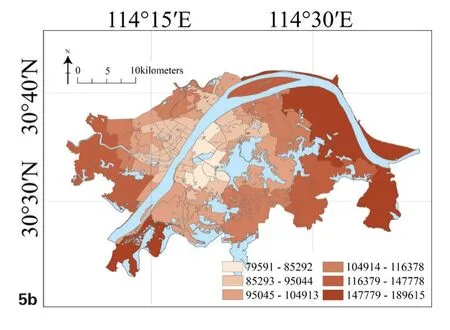
图5 b 武汉各街道道路综合可达性Ak分布

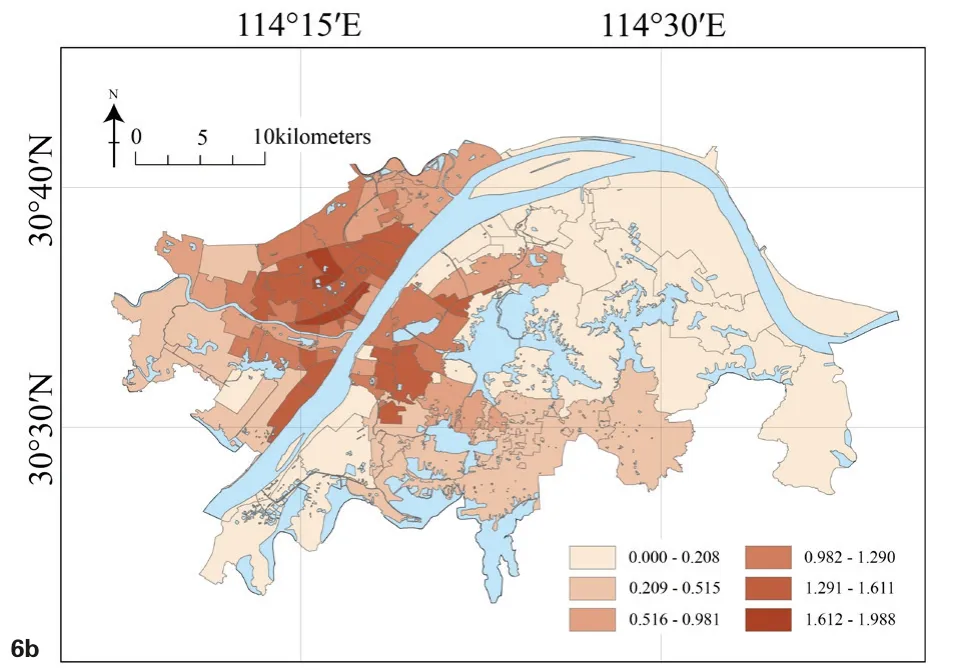
图6 b 武汉各街道轨道交通站点覆盖度Bk分布

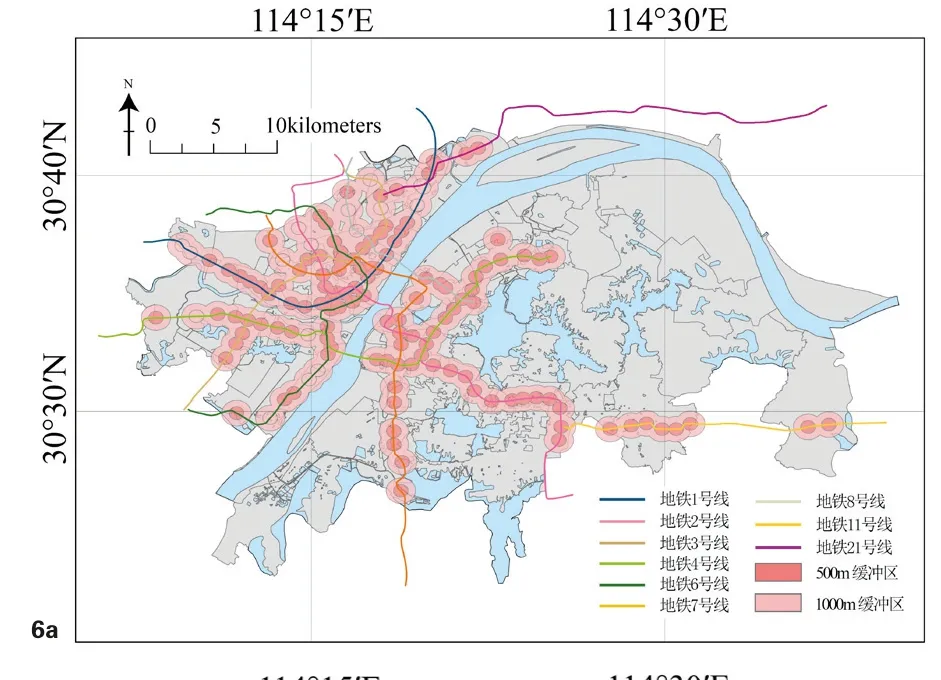
图6 a 武汉轨道交通站点缓冲区分布

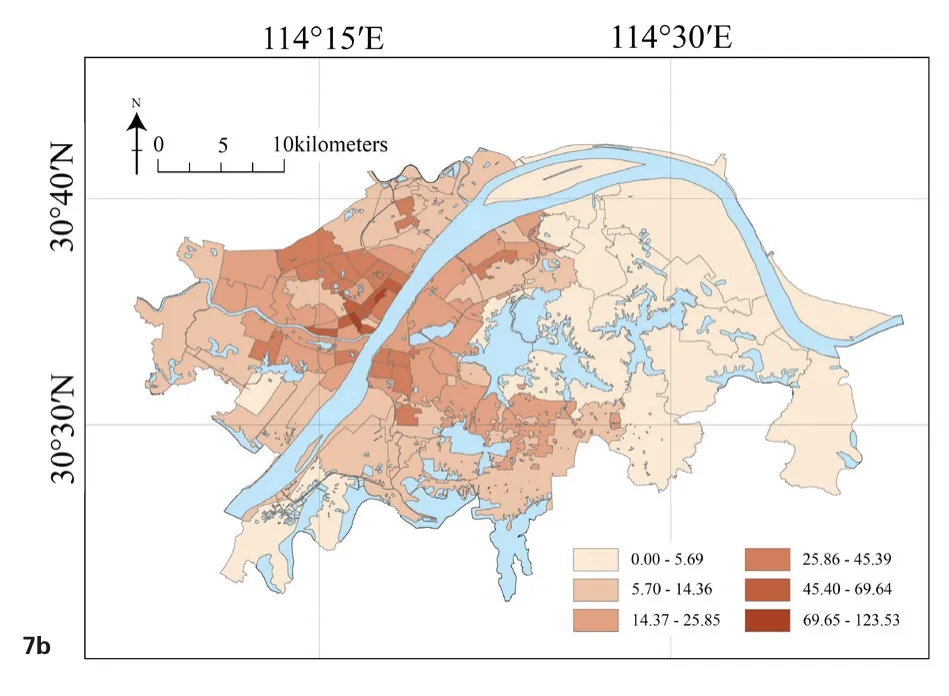
图7 b 武汉各街道公交站点分布密度Sk分布

图7 a 武汉公交站点核密度分布

（1）路网密度

路网密度反映某区域的道路密集程度，路网密度值越高表示该区域居民出行时享有道路资源越多。本文各街道路网密度值Dk的计算公式如下：

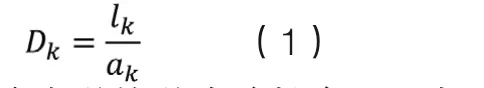
其中lk表示该街道的道路总长度，ak表示该街道的占地面积。

（2）道路可达性

道路可达性反映城市居民机动出行的便捷程度。本文对武汉不同等级道路赋予不同的车辆行驶速度，其中绕城高速100km/h，快速路80km/h，主干道60km/h，次干道40km/h，支路以及各类小路20km/h。然后基于ArcGIS10.7对武汉的城市道路进行网络分析，首先以城市中的全部道路交叉口为节点进行时间成本的OD矩阵计算[16，17]，然后求得该街道的道路综合可达性值Ak，其计算公式如下：

其中Tij为城市中i、j两点间的时间成本，dij为i、j两点间的距离成本，vij为i、j两点间的平均速度，Ai为i点处的单点可达性值，n为该街道所包含的道路交叉口节点数量。

（3）轨道交通站点分布

轨道交通多位于城市的地下封闭空间，单车客运量较大，人流的聚集程度很高，可能容易导致疫情的快速传播。此外轨道交通主要承担了城市的远距离跨区域客运，表现出的是“出行距离导向”，即乘客选择轨道交通出行主要在于出行距离的考虑，某一站点的客流量主要取决于该站点辐射范围内有相关出行需求的居民数量。一般而言城市中距离轨道交通站点500m范围内的住房被称为“地铁房”，而1000m范围内的住房则被称为“准地铁房”[15]，原因在于距离轨道交通站点500～700m，即10min以内的步行距离较容易被乘客所接受[18]，而Wibowo等在对于新加坡案例的研究中发现90%的乘客最大可承受步行距离约为1000m[19]，且Hyungun Sung等发现距离轨道交通站点500m以内的客流量约为距离站点500～1000m范围内客流量的2倍[20]。由此本文考虑“地铁房”和“准地铁房”内居民出行受到轨道交通站点影响较大，从而以研究区域内的全部轨道交通站点为中心设置双重缓冲区，第一重为500m缓冲区，第二重为1000m缓冲区，赋予500m缓冲区双倍于1000m缓冲区的面积权重，然后计算每个街道的双重缓冲区加权面积之和，并将其与街道占地面积的比值定义为该街道的轨道交通站点覆盖度Bk。该指标可反映武汉居民乘坐轨道交通出行的便捷程度，其计算公式如下：

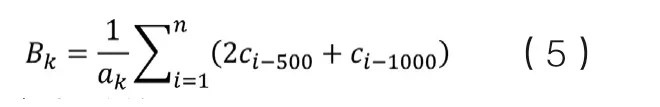
其中ak为该街道的占地面积，ci-500为该街道中第i个轨道交通站点周边500m缓冲区面积，ci-1000为该街道中第i个轨道交通站点周边1000m缓冲区面积。

（4）公交站点分布

城市公交虽然与轨道交通同为城市中最为常规的公共交通工具，但是两者在运输距离、客流强度和空间封闭程度等方面均存在显著差别，这也使得两种交通工具对于疫情传播可能具有不同的影响特征，因此城市公交与轨道交通应当作为不同的影响因素被予以分开考虑。城市公交出行以短程或轨道交通覆盖盲区为主，表现为“线路选择导向”，即乘客选择城市公交出行主要在于该公交线路契合自己的出行需求，公交线路丰富的站点可能吸引更多的乘客[21，22]，由此本文对公交站点本身的分布密度以及每个站点的公交线路数量进行了叠加考虑，计算城市各街道单位面积内每个公交站点的公交线路数量之和，并将其值定义为该街道的公交站点分布密度Sk，其指标可反映武汉居民乘坐公交出行的便捷程度。计算公式如下：

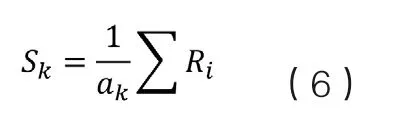
其中Ri为该街道内经过第i个公交站点的公交线路数量，ak为该街道的占地面积。

1.4 研究方法

本文采用OLS模型和GWR模型进行统计检验以分析上文所述的路网密度、道路可达性、轨道交通站点分布和公交站点分布等4个交通驱动因素对于武汉疫情传播的影响特征。其中OLS模型主要用于分析单一因变量和多个自变量之间的关联问题，该模型能够对参数进行平均或全局意义上的估计，并基于估计结果进行因子筛选。而GWR模型则是Brunsdon等人对OLS模型的延伸[23]，其能够将自变量发生点的空间位置加入回归参数中，使得变量间的关系也跟随空间位置的变化而改变，并以每个样本空间位置间的衰减函数为权重进行回归分析，然后赋予不同样本以相应的权重，从而能有效处理空间相关性和空间异质性问题[24，25]。在本文中由于路网密度、道路可达性、轨道交通站点分布和公交站点分布等自变量和作为因变量的感染密度均是以坐标数据的形式呈现并由此具有一定的空间属性，因此应用GWR模型能够更好的进行变量空间异质性的线性回归分析。但由于GWR模型对变量间多重共线性较为敏感，使得其选用的变量不宜过多，所以常在进行GWR分析前首先采用OLS模型进行回归分析，以剔除干扰因子，从而确保GWR模型分析的准确性[26]。

OLS模型和GWR模型的表达式分别如下式（7）和（8）所示：

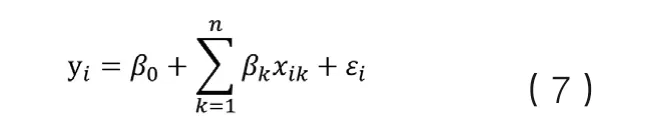
其中yi为第i个样本的因变量，β0为线性回归方程的截距，βk为第k个自变量的回归系数，xik为第k个自变量在i上的取值，εi为算法残差。

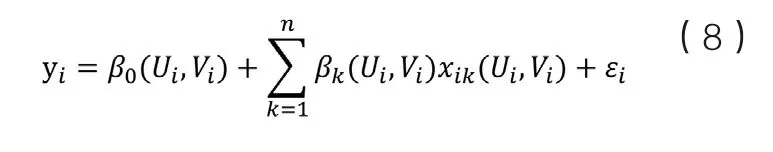
其中β0(Ui，Vi)为(Ui，Vi)空间位置的GWR截距，βk(Ui，Vi)为第k个自变量在(Ui，Vi)空间位置上的加权回归系数，xik(Ui，Vi)为第k个自变量在(Ui，Vi)上的取值，εi为算法残差。

GWR模型的关键在于空间权重矩阵的设置，本文基于ArcGIS10.7选择高斯函数作为GWR模型分析的核函数，核函数类型为固定型，其表达式为：

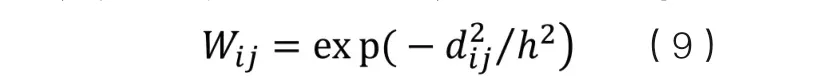
其中dij为样本i和样本j的空间距离，h为最优带宽。GWR模型对于带宽的选择较为敏感，带宽过大或过小都可能对模型拟合精度产生影响。由此基于ArcGIS分析平台，选择赤池信息量准则（Akaile Information Criterion，AIC）法确定最优带宽，当模型的AICc 值最小时即可确定最优带宽[27]。

2 结果分析

2.1 空间相关性验证

通过空间相关性全局统计分析以及相应的局部统计分析，本文对武汉COVID-19分布的空间相关性以及集聚程度进行了检验[24，28]。

空间相关性全局统计分析包括空间自相关性分析与高/低聚类分析，其结果（表1）拒绝了武汉各街道的感染密度不具有空间相关性的假设。在空间自相关性分析中，全局莫兰指数为0.375，表明武汉各街道的感染密度存在空间正相关，而高/低聚类分析的z值为4.389则表明该空间相关性在感染比例较高的区域更为明显。

表1 武汉疫情分布的空间相关性全局统计结果

在局部统计分析中，首先通过局部莫兰指数分析（图8）武汉中心城区各街道存在的感染密度高—高集聚、低—高异常和低—低集聚等3种类型。其中高—高集聚主要出现在汉口、武昌、汉阳的临江核心地带，该地区为武汉传统中心城区，人口分布密集且各类交通设施发达；低—低集聚出现在武汉东北部，主要分布钢铁、化工等重型工业企业，区域内社会生活自成体系，居民跨区域出行需求较低，且远离武汉中心城区，对外交通较为不便；低—高异常则主要出现在武汉二环线以内的地区，且与高—高集聚交错分布，该地区同样为武汉市人口较多且交通较为便利的区域。此外进一步利用热点分析对统计显著性高值区域和低值区域分别进行空间聚类识别，从而验证了前文所述的各街道感染密度分布特征（图9）。以上验证结果仅能说明在武汉城市中心区域COVID-19感染密度的空间相关性更为显著，但是不同交通驱动因素对于疫情传播的具体影响特征尚无法明确，对此本文进一步引入OLS模型和GWR模型对该问题进行分析。

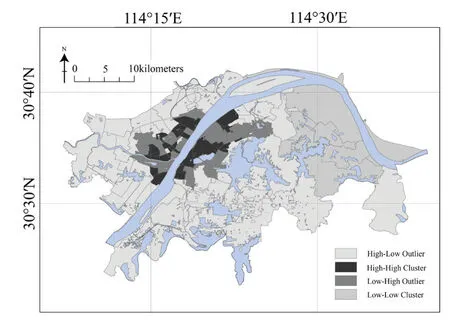
图8 武汉疫情分布的局部莫兰指数分析

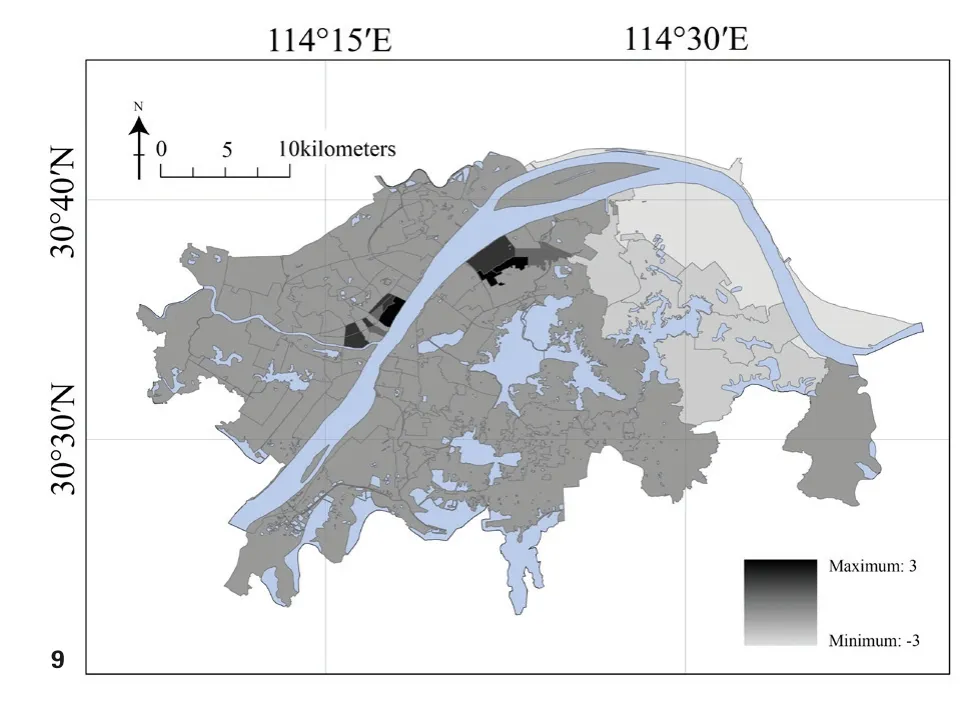
图9 武汉疫情分布的热点分析

2.2 OLS模型分析

为了减少变量间多重共线性对GWR模型带来的影响，首先利用OLS模型进行整体线性回归拟合分析，以获得较为准确的变量组合。将变量的数据标准化后，OLS模型分析结果如表2所示，作为城市交通驱动因素的各变量VIF值均低于7.5，因此变量不存在冗余现象。各变量中道路综合可达性值Ak、轨道交通站点覆盖度值Bk以及公交站点分布密度值Sk通过了稳健p值≤0.05的显著性检验。其中公交站点分布密度与轨道交通站点覆盖度的回归系数为正值，尤其轨道交通站点覆盖度的回归系数值达到了7.998，是各有效变量中的最高值，也说明在本文所述的各类交通驱动因素中轨道交通站点分布对于武汉COVID-19分布的影响最大。此外道路综合可达性的回归系数为负值，而路网密度作为变量之一未能通过显著性检验，说明其与疫情分布之间的关联性较弱，如继续使用GWR模型进行分析可能会导致不可知的错误产生，故为了降低GWR模型的复杂度，之后的GWR模型分析中将该变量予以排除。

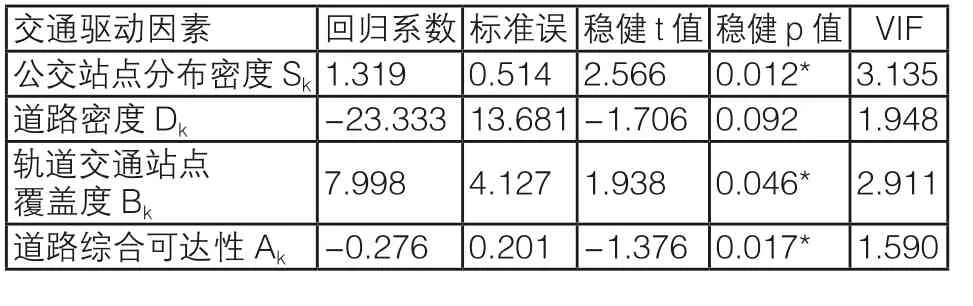
表2 武汉疫情分布的OLS模型分析结果

为了比较OLS模型和GWR模型的分析有效度，本文将对这两个模型的调整R2和赤池信息准则进行对比。在OLS诊断中R2值为0.359，而调整后的R2值为0.331，表示OLS模型能够拟合和解释因变量总变异的约33.1%，此外在ArcGIS10.7中基于高斯函数以及交叉验证法确定OLS模型的最优带宽后AICc值为1054.49。上述诊断结果可与下文的GWR模型进行分析有效度对比。

2.3 GWR模型分析

基于上述的OLS模型分析结果，在GWR模型分析时将道路密度因素剔除。在对于影响武汉各街道感染密度的交通驱动因素识别中GWR模型具有更高的稳定性，其R2值为0.631，较之于OLS模型的R2值提高了75.77%。此外本文中GWR模型的AICc值为1049.45，较之于OLS模型的AICc值减小了5.04，而一般情况下AICc值减小3.00即可认为该模型的分析有效度显著提升[29]。由此可见GWR模型较之于OLS模型分析有效度更高，因此下文将基于GWR模型分析各交通驱动因素对于武汉COVID-19传播的影响特征。

在GWR模型中标准化残差以随机分布为宜，可据此判断模型有效性。根据标准化残差分布可知（图10），武汉各街道仅有钢花村街道一处标准化残差大于2.5倍标准化残差，表明该街道可能存在数据偏差，但相比于全部的93个研究单元，该误差对整体不产生较大影响，即通过残差检验。此外基于莫兰指数的模型扩展检验（表3）显示该GWR模型的标准化残差置信度大于99%，不存在空间集聚或离散，基本符合随机分布的特征。

表3 GWR模型的标准化残差莫兰指数检验

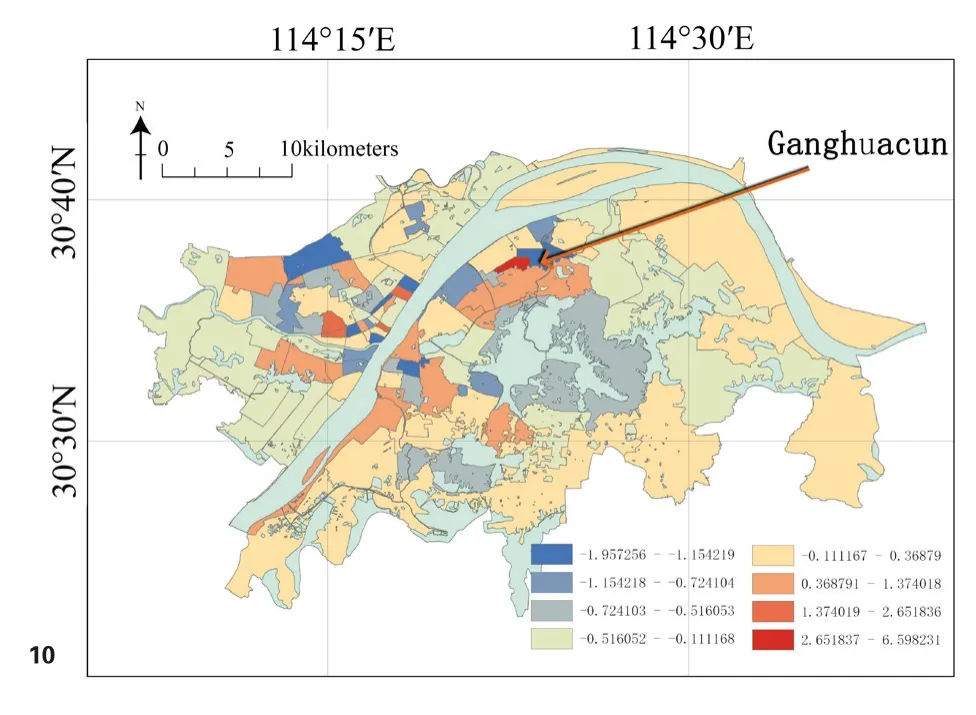
图10 GWR模型的标准化残差分布

在剔除了作为前文所述干扰因素的城市路网密度Dk后，城市道路综合可达性Ak、轨道交通站点覆盖度Bk以及公交站点分布密度Sk的回归系数如表4所示，可知在地理加权回归分析中武汉各街道的轨道交通站点覆盖度以及公交站点分布密度依然与其感染密度呈现正相关，而道路综合可达性则继续与感染密度负相关。由此可见地铁、公交等城市公共交通明显加剧了疫情的传播，尤其轨道交通站点覆盖度这一指标在GWR模型中的回归系数高达7.464，说明其与COVID-19的传播具有极强相关性。轨道交通的人流量明显大于城市公交，也因此其更易导致病毒的快速传播[30]，这也是武汉轨道交通与疫情分布的相关性较之于城市公交更强的主要原因。道路综合可达性作为影响疫情分布的另一个驱动因素主要反映了城市居民机动出行的便捷程度，在GWR模型中武汉的道路综合可达性与感染密度呈现负相关，这说明采用非公共交通的方式机动出行大幅度减少了人群之间的接触，因此疫情的传播有所减缓。

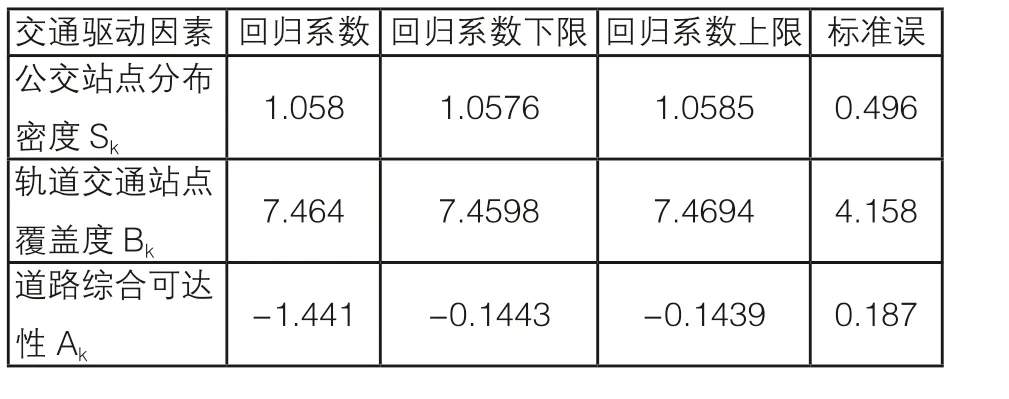
表4 GWR模型分析结果

武汉各街道公交站点分布密度的GWR回归系数分布如图11所示，可见回归系数值呈现“南北高中间低”的态势，城市最为核心区域的回归系数值明显较低，而回归系数值最低处则出现在远离长江主轴的城市远郊地带。较之于城市中心，武汉南、北两大区域的轨道交通覆盖度较低，仅部分郊区线路能够通达，如位于武昌南部的7号线、位于汉阳南部的6号线以及位于汉口东北部的阳逻线等。这两大区域在轨道交通线路稀缺的同时居住却较为密集，武昌南部的白沙洲片区和南湖片区、武昌北部的青山片区、汉阳南部的四新片区以及汉口东北部的后湖片区等都是武汉规模较大的集中性居住区域，因此居民的公共交通出行多数仅能依靠城市公交，从而导致了这两大区域的疫情传播可能与公交站点分布有着较为密切关系。反之武汉城市中心区域轨道交通网络已经成熟，居民出行可以较多依赖于轨道交通，因此公交站点分布对于疫情传播的影响偏弱，而远离长江主轴的城市远郊地带人口居住分散且城市公交线路稀少，此类区域的公交站点分布显然无法对疫情传播造成有效影响。由以上分析可知武汉轨道交通覆盖尚未完善的区域城市公交对于疫情传播有着更为明显的影响，而在轨道交通覆盖已完善的中心城区城市公交对于疫情传播的影响程度则明显减弱。

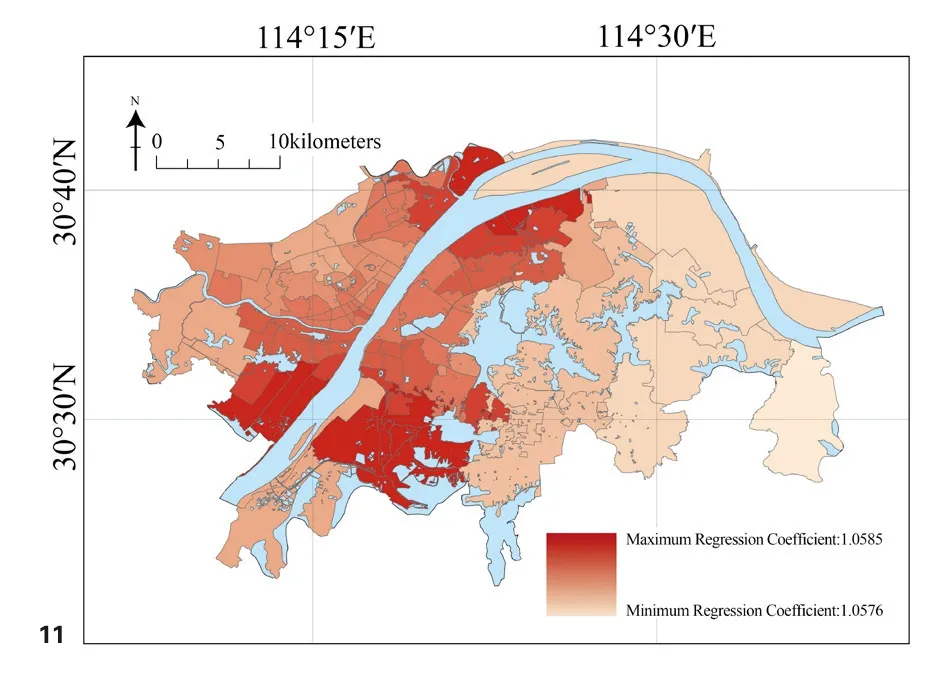
图11 武汉各街道GWR回归系数（公交站点分布密度）分布

武汉各街道轨道交通站点覆盖度的GWR回归系数分布如图12所示，可见回归系数值较高的区域正好位于城市中心，并由西北向东南呈带状分布，而回归系数值最低的区域则是位于武昌北部的青山区。武汉中心城区轨道交通线网密集且客流量大，其中作为武汉城市主动脉的2号线自西向东几乎贯穿了全部回归系数高值区域，该线路单日客运量长期超过100万人次，远高于武汉其他任何线路，武汉大量高校、商圈、金融中心、客运枢纽以及高新产业园区等皆由2号线所串联，也由此形成了疫情期间横贯武汉东西的“感染桥梁”。2号线是武昌中心城区唯一的东西向轨道交通线路，该路段的客流强度长期居于整个2号线的最高位，这导致了其周边区域的回归系数值更高。武昌GWR回归系数值最高的区域为武昌的中南部地区，而这一区域正是2号线与7号线、4号线的换乘区域，2、4、7号线是武昌客流量最大的3条线路，且该区域也是武昌轨道交通站点分布最为密集的地区。此外1号线、3号线等其他客流大线周边的回归系数值也较高，而回归系数值最低的青山区尚未运行任何轨道交通线路，且该行政区内就地置业的工业人口居多，跨区域通勤需求量不大，从而导致轨道交通对于疫情传播的影响不明显。由以上分析可知武汉轨道交通在线网密集的情况下对于疫情传播可造成极为显著的影响，甚至易于由此形成疫情传播的“高速走廊”。

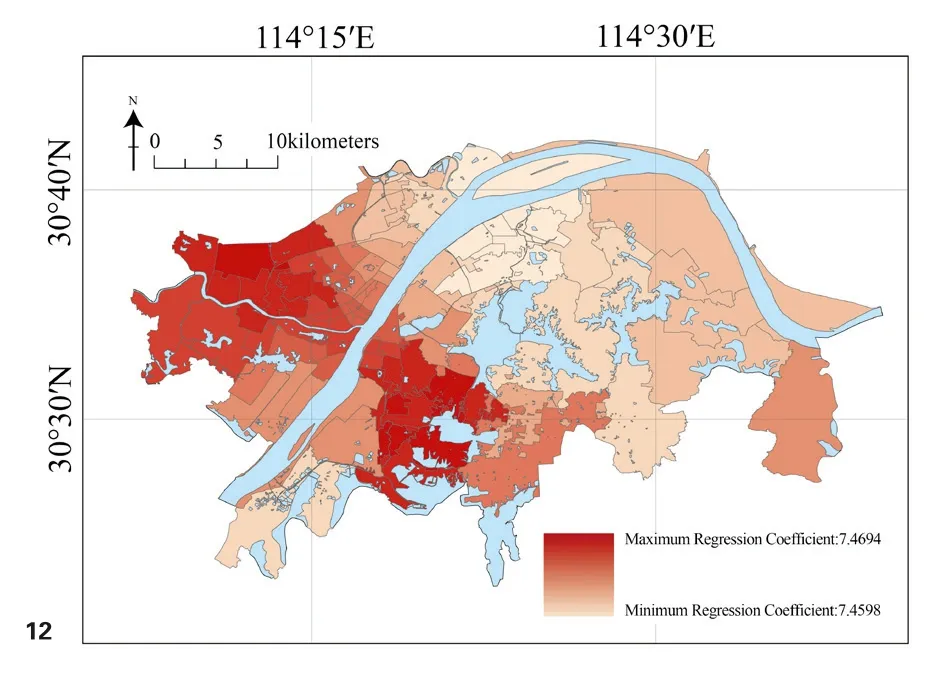
图12 武汉各街道GWR回归系数（轨道交通站点覆盖度）分布

武汉各街道道路综合可达性的GWR回归系数分布如图13所示，研究区域内全部93个街道的回归系数皆为负数，说明各街道的道路综合可达性均与疫情传播负相关。图中回归系数的绝对值呈现北高南低态势，说明武汉南部区域道路可达性对于疫情传播的影响更小，其主要包括武昌东湖、沙湖以南的大部分地区以及汉阳的部分地区，武汉的大中专院校及高新技术企业多聚集于此，因此人口结构较之于武汉北部地区更为年轻化且外来人口更多。COVID-19疫情爆发后武汉于2020年1月23日正式封城，此时临近中国传统春节，绝大多数大学生和外来人口均已返乡，导致武汉南部区域感染密度的统计数据可能略偏小。此外大学生及外来人口的汽车保有率明显不及武汉当地居民，该类人群日常出行只能以公共交通为主，所居住区域的道路通达情况难以影响其对于出行方式的选择，这进而导致该区域道路可达性对于疫情传播的影响程度也有所减弱。而武汉北部如汉口、青山等地多为当地居民，因此道路可达性对于疫情传播有着更为明显的影响。由以上分析可知武汉各区域的道路可达性对于疫情传播有一定程度的负向影响，但是在人群过于依赖公共交通的区域道路可达性对疫情传播所形成的影响可能并不显著。

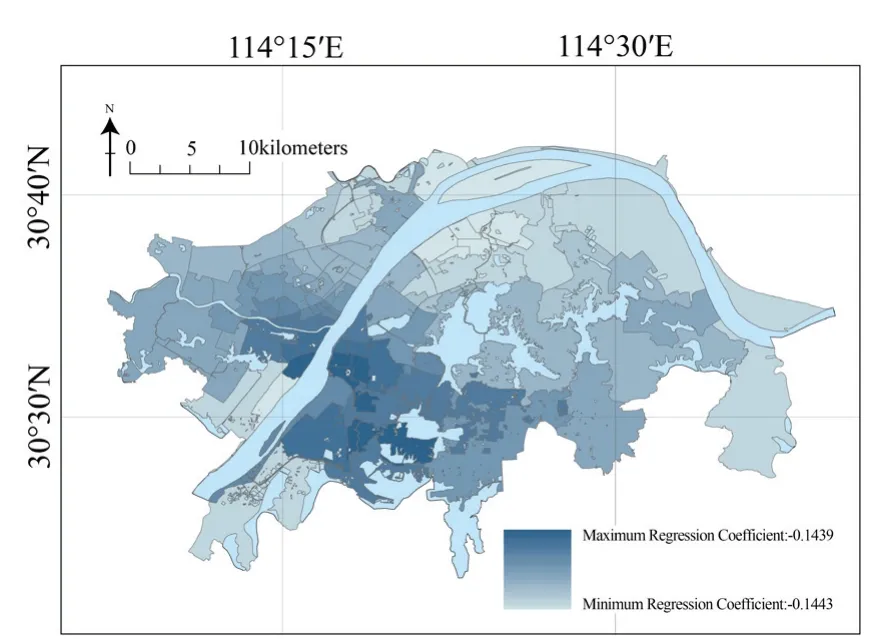
图13 武汉各街道GWR回归系数（道路综合可达性）分布

3 结论与建议

3.1 结论

基于上述以湖北省武汉市为例的研究，本文认为城市交通对于疫情传播可能存在如下影响特征如下：

（1）在城市各区域的路网密度、道路可达性、轨道交通站点分布以及公交站点分布等4个典型交通驱动因素中，路网密度因素对于疫情传播的影响最不显著，而道路可达性、轨道交通站点分布以及公交站点分布等3个驱动因素均可能对于疫情传播造成影响，其中轨道交通站点分布和公交站点分布与疫情传播正相关，而道路可达性与疫情传播负相关。

（2）轨道交通站点分布因素与疫情传播之间存在显著的正相关性，部分客流量大的线路甚至可能成为疫情传播的“高速走廊”。公交站点分布因素与疫情传播之间也存在一定的正相关性，但是相关度低于轨道交通站点分布因素，此外在轨道交通覆盖尚未完善的区域公交站点分布对于疫情传播有着更为明显的影响，但是在轨道交通覆盖完善的区域其影响程度则明显减弱。

（3）道路可达性因素与疫情传播之间存在负相关性，但是在人群过于依赖公共交通出行的区域道路可达性对疫情传播所造成的影响可能并不显著。

3.2 交通优化建议

基于本文结论，人口聚集型城市可构建有效的城市交通“平疫转换”体系，并基于此加强城市的韧性交通建设，以作为应对如COVID-19等呼吸道传染病的交通优化措施[31]。

如前文所述，轨道交通对于疫情传播的正向作用最为显著，其次为城市公交，而由于道路可达性对于疫情传播存在负向作用，这表明自驾车出行可有效延缓疫情的传播速度。虽然高强度的公共交通出行总体上并不利于疫情防控，但是人口的聚集与流动本是城市繁荣的标志，而完善且高效的公共交通体系则是现代城市运转的有利保障，因此不应“因噎废食”，由此便机械性限制城市公共交通发展并迫使人群采取更高能耗的自驾车方式出行。正所谓“润物细无声”，完善的秩序往往建立于未觉之处，城市交通“平疫转换”体系的构建亦是为了对疫情防控期间的居民出行施以柔性引导。

对此在城市交通规划中可制定应对疫情的分级预案，根据整个城市或城市中特定区域的疫情风险级别将交通运行划分为轨道交通出行限制、公共交通出行限制（进一步包含公交、轮渡等出行限制）、机动车出行限制（进一步包含自驾车出行限制）、车辆出行限制（进一步包含非机动车出行限制）和完全出行限制等由高至低的不同限制等级。通过制定不同限制等级的相应预案，当其中某一项限制等级触发时，城市能够在这一区域内立即启动以次一等级出行方式为主的交通补偿措施，从而在未来分区、分级、精准开展疫情常态化防控的指导思想下尽可能兼顾城市的有效运转以及居民的正常生活。完成该分级预案的核心在于城市不同区域出行方式的脆弱性识别，对此需进一步抽样统计城市各区域居民的日常出行方式、出行路线与出行距离，由此判定对每一等级出行方式存在刚性依赖的人群比例及其主要流动方向，从而得以对特定出行方式存在较高脆弱度的区域提前制定补偿措施，如向受到轨道交通出行限制影响较大的区域调度定向接驳公交，向受到公共交通出行限制影响较大的区域科学分配私家车路权，向受到机动出行限制影响较大的区域调度额外的共享单车等非机动交通工具，以及向受到车辆出行限制影响较大的区域开放更多的步行路权等，最终在疫情发生之时实现“空间换时间”的防疫效果，延缓病毒传播的速度。以上工作也是城市韧性交通体系建设的重要组成部分。

除此之外应当高度重视城市慢行交通体系的建设，尽可能将“城市绿道”模式从临水、临山、临田等风景区引向城市内部，并使其成为城市交通体系的一部分，以引导更多居民采取非机动形式健康出行，从而在疫情发生之时能够更高效完成平疫转换。当前还应以交通大数据助力于城市的智能化管理，在交通运行中不仅着眼于现状监测，更应强调动态预警，利用流动数据甄别高风险的区域与人员，据此指导城市交通防疫策略的制定。

图、表来源

图1～13：均为作者根据数据结果绘制。表1～4：作者基于分析结果整理绘制。