织物结构对拉伸性能的影响有限元分析
孙一万,张学文,蔡利海,邵伟光,刘文言
(1.中国矿业大学(北京) 机电与信息工程学院, 北京 100083; 2.军事科学院 系统工程研究院军事新能源技术研究所, 北京 102300; 3.北京航天发射技术研究所, 北京 100076)
随着可扁平输送软管在油料输送、消防应急、排水排涝、农业灌溉等领域的广泛应用[1-2],对承压强度高、单位质量轻的可扁平输送软管的需求逐渐增加。可扁平输送软管的管体为织物增强柔性复合材料,主要由内胶层、织物增强层和外胶层组成,其中织物增强层为承压结构,是由圆织机编织的平纹或斜纹织物,研究增强层的纱线粗细和间距、图案的组织结构与力学性能的关系对优化增强层的受力状态、提升可扁平输送软管的承压强度有重要意义[3]。
有限元模拟是研究织物力学性能的常用方法。刘倩楠等[4]、李瑛慧等[5]分别对三原织物的拉伸过程进行了模拟,研究了三原组织织物的拉伸性能;Su等[6]建立了6种混纺织平纹织物和斜纹织物模型,并对6种织物拉伸过程中的应力应变和收缩率进行了分析;Valter等[7]研究了单丝平纹织物的单轴拉伸和双轴拉伸的宏观力学响应。以上研究的织物对象主要是已经商业化生产的织物,对结构参数与织物拉伸性能的关系研究得不够系统。为了解决这一问题,本文主要基于可扁平输送软管增强层的结构参数进行实验设计,系统研究了织物结构参数与拉伸性能的关系,并就织物结构对可扁平输送软管承压强度的影响进行了分析。首先对现有可扁平输送软管增强层进行拉伸试验和有限元模拟,通过对比拉伸试验和模拟的结果验证了模拟方法的准确性,然后根据现有增强层的结构参数建立了不同经纱间距、不同纬纱粗细的平纹和斜纹织物的三维模型,并通过有限元模拟系统地研究了经纱间距、纬纱粗细和组织图案和纬向织缩率对织物拉伸性能的影响,最后结合仿真结果分析了织物结构对可扁平输送软管承压强度的影响。
1 有限元模拟准确性验证
1.1 增强层拉伸试验
本文仅对织物增强层纬向拉伸过程进行探讨。首先将可扁平输送软管织物增强层从软管胶层中剥离出来,然后从织物中间区域沿纬纱方向裁剪出尺寸为300 mm×20 mm的矩形布条,最后从试样左右两边各扯掉1根纬纱,得到图1(a)中包含5根纬纱的试样。将试样固定在图1(b)所示的AI-7000M伺服控制拉力试验机中(Gotech公司),原始标距200 mm,试验过程中拉力试验机的下夹具固定,上夹具以100 mm/min的恒定速度向上运动,直到试样断裂。

单位:mm。图1 增强层试样和拉伸试验Fig.1 Specimen of enforcement layer and tensile test. (a)Specimen of enforcement layer;(b)Tensile test
1.2 增强层拉伸有限元模拟
1.2.1 增强层的几何模型
为了得到织物增强层结构参数的准确值,首先使用显微镜对增强层织物的横截面进行拍照,图2为织物增强层横截面照片,可以看出纱线的横截面为椭圆,w和t分别为纱线横截面的长轴和短轴,p为纱间距,k为纱线卷曲高度,下角标1和2分别表示经纱和纬纱[8-9]。然后利用图像测量软件测量结构参数,测量得到的结构参数列在表1中。根据中心线法则和表1中的结构参数,以正弦函数作为纱线中心线的轨迹函数[10],使用三维建模软件SOLIDWORKS建立增强层的三维模型,图3为增强层的三维模型。
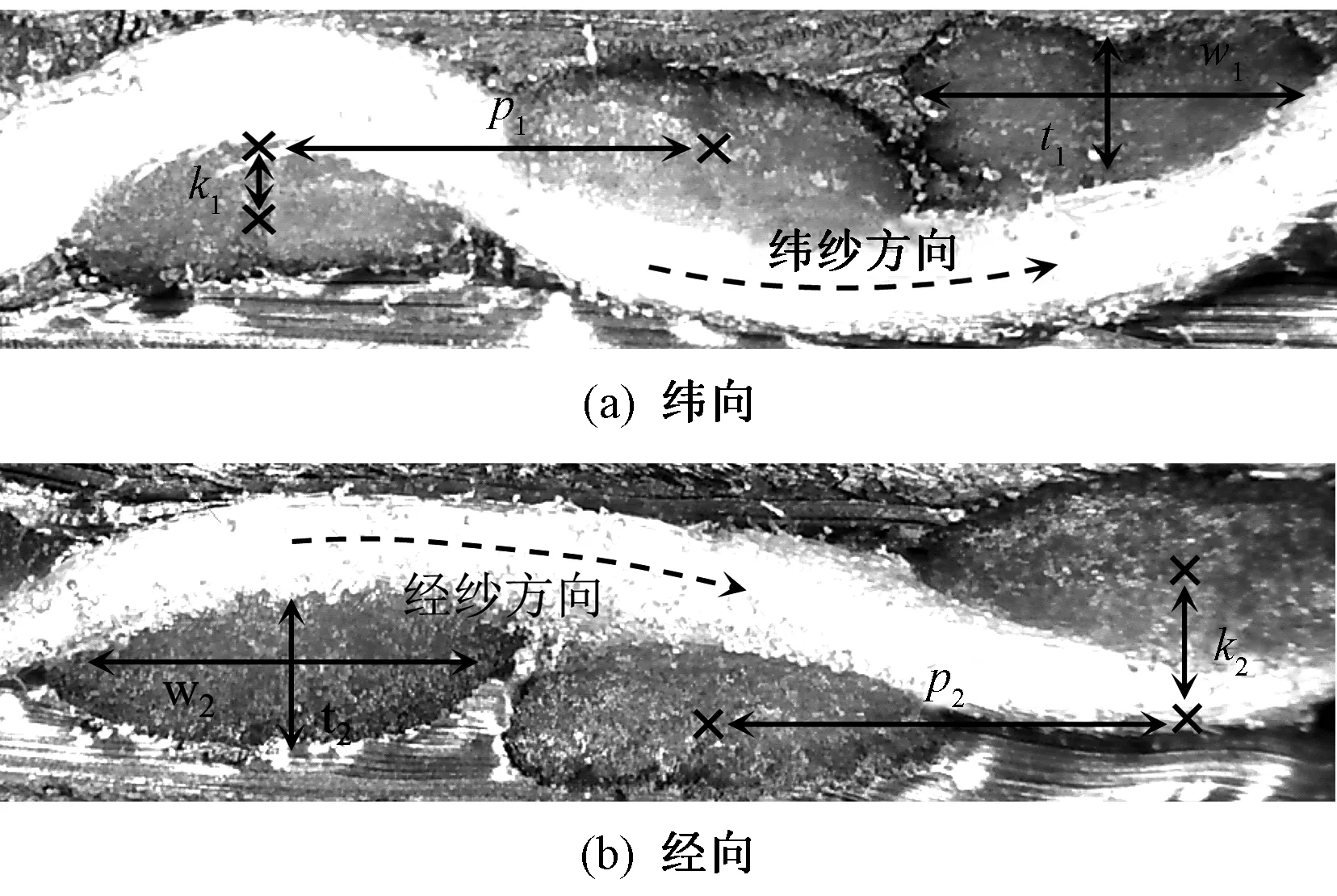
图2 增强层横截面(×30)Fig.2 Cross-section of enhancement layer.(a)Weft section;(b)Warp section

表1 增强层的结构参数Tab.1 Structural parameters of enforcement layer mm

图3 增强层的三维模型Fig.3 Three-dimensional model of enhancement layer
1.2.2 纱线材料行为定义
为了得到纱线的力学数据,使用伺服控制拉力试验机进行纱线拉伸试验,原始标距100 mm,拉伸速度100 mm/min,经纱和纬纱分别进行5次拉伸测试。图4为经纱和纬纱的拉伸应力-应变曲线。可以看出,经纱和纬纱表现出模量随应变逐渐增加的超弹性材料力学行为[11],因此在将经纱和纬纱的拉伸试验数据导入ANSYS Workbench后,通过调用材料库中的超弹性材料本构模型来拟合经纱和纬纱的拉伸试验数据,从而定义经纱和纬纱的力学行为。
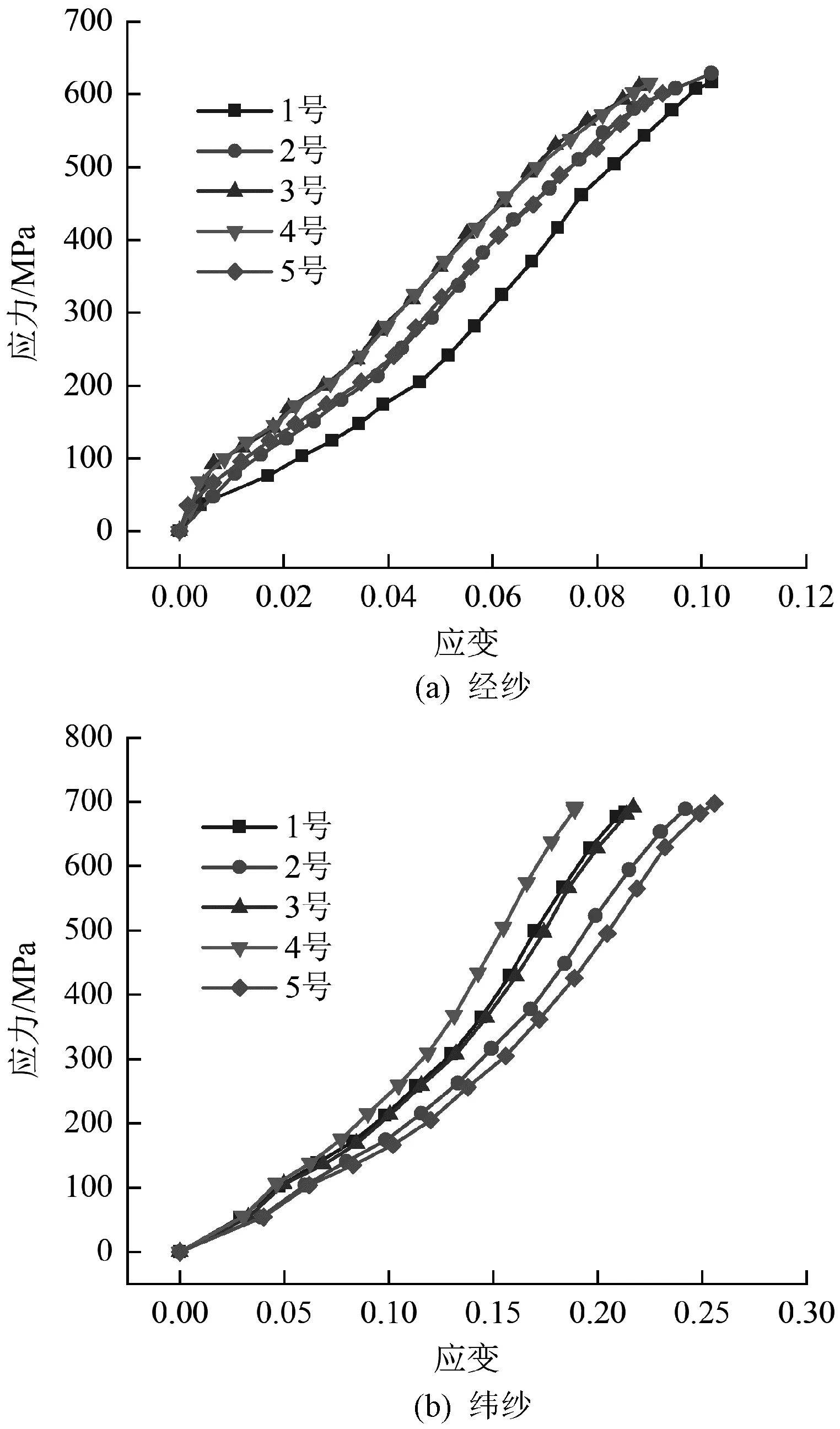
图4 经纱和纬纱的拉伸应力-应变曲线Fig.4 Warp and weft tensile stress-strain curves.(a)Warp;(b)Weft
1.2.3 接触定义
接触类型设置为Frictional,摩擦因数设置为0.38[12]。因为经纱和纬纱的表面性质相同,所以目标面和接触面的采用软件默认设置。接触算法设置为Pure Penalty,接触产生的穿透会导致计算结果的准确度下降,甚至得到没有任何物理意义的计算结果,而Pure Penalty在每一对接触面内增加了一个接触刚度,通过调整接触刚度可以保证在较小的穿透下就能得到收敛的计算结果。
1.2.4 网格划分
为了保证模型大变形时仍然能够得到收敛且准确的计算结果,模型划分网格时需要选择对大变形具有较好适应能力的单元。经过一系列尝试计算,选择Solid185单元进行网格划分。
1.2.5 边界条件
图5描绘了纬向拉伸时对增强层施加的边界条件。织物平面与Z轴垂直,纬纱与X轴方向平行,经纱与Y轴方向平行。约束经纱上端面和下端面Z方向的位移,对纬纱左端面施加固定约束,约束纬纱右端面Z和Y方向的位移。根据增强层的拉伸试验数据,在每根纬纱右端面施加1 193 N沿X轴正方向的拉力。
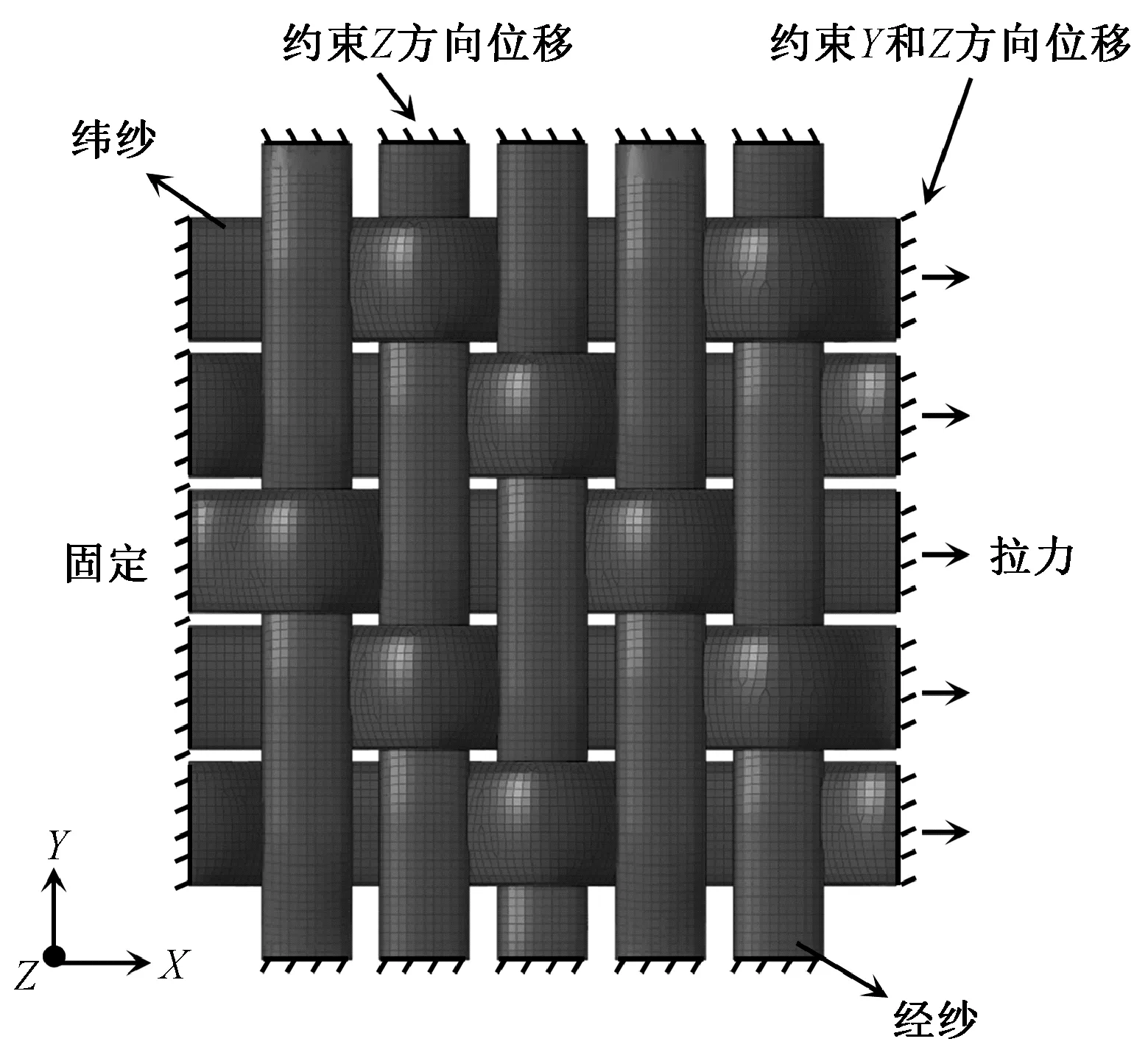
图5 纬向拉伸边界条件Fig.5 Boundary condition in weft tension
1.2.6 分析设置
将牛顿-拉普森选项设置为非对称,载荷步设置为100,最小载荷子步和最大载荷子步分别设置为1和100,打开大变形开关,然后计算求解。
1.3 有限元模拟准确性分析
为了验证有限元模型的准确性,将增强层纬向拉伸试验和有限元模拟的应力-应变曲线在图6中进行对比。可以看出,有限元模拟和拉伸试验的结果基本吻合,证明本文使用的模拟方法可以很好地预测增强层承受纬向拉伸载荷时的力学性能。织物的模量随应变的增加逐渐增加是由于纱线在织物中的轨迹包括曲线段和直线段,在低应变区,纱线中的曲线段随着织物应变的增加逐渐被拉直,所以拉伸模量低,而在高应变区,织物应变的增加主要来自纱线的伸长,所以拉伸模量高。图7展示了织物增强层拉伸有限元模拟的等效应力分布云图。红色指示应力最大区域,最大应力出现在经纱和纬纱的交叉点,说明织物承受拉伸载荷时在交叉点处更容易产生应力集中现象。
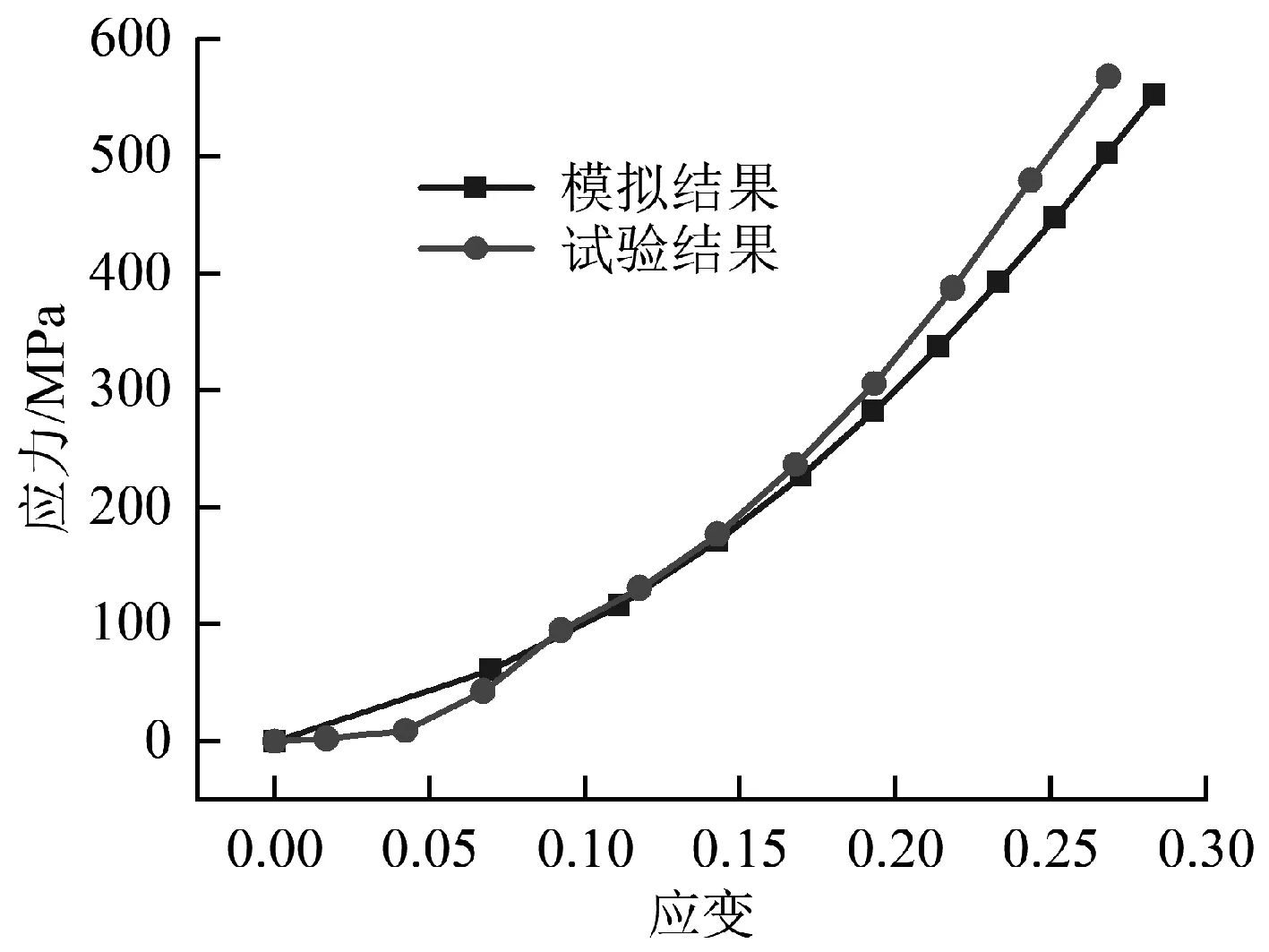
图6 增强层纬向拉伸试验与有限元模拟应力-应变曲线Fig.6 Stress-strain curves of tensile test and FEA simulation of enforcement layer

图7 增强层纬向拉伸有限元模拟等效应力分布云图Fig.7 Contour of equivalent stress distribution of FEA simulation of enforcement layer in weft tension.(a)Contour of equivalent stress distribution of enforcement layer;(b)Contour of equivalent stress distribution of weft
2 不同结构的织物拉伸有限元模拟
2.1 织物的三维模型
纱线横截面积的大小决定了纱线的粗细,纱线横截面长轴与短轴比值恒定时,可以用纬纱横截面短轴的长度表示纬纱的粗细。根据表1中增强层的结构参数,保持纬纱横截面长轴与短轴的比值为2.75,仅改变纬纱横截面短轴长度,分别建立图8、9中纬纱短轴长度t分别为1.0、0.8、0.6 、0.4、0.2 mm的平纹和斜纹织物的三维模型;同样根据表1中的数据,仅改变经纱间距,建立图10、11中经纱间距p分别为2.6、3.4、4.2、5.0、5.8、6.6 mm的平纹和斜纹织物的三维模型。

图8 纬纱粗细不同的平纹织物的3D模型Fig.8 Three dimensional-models of plain fabrics consist of weft with different thickness

图9 纬纱粗细不同的斜纹织物的3D模型Fig.9 Three dimensional-models of twill fabrics consist of weft with different thickness
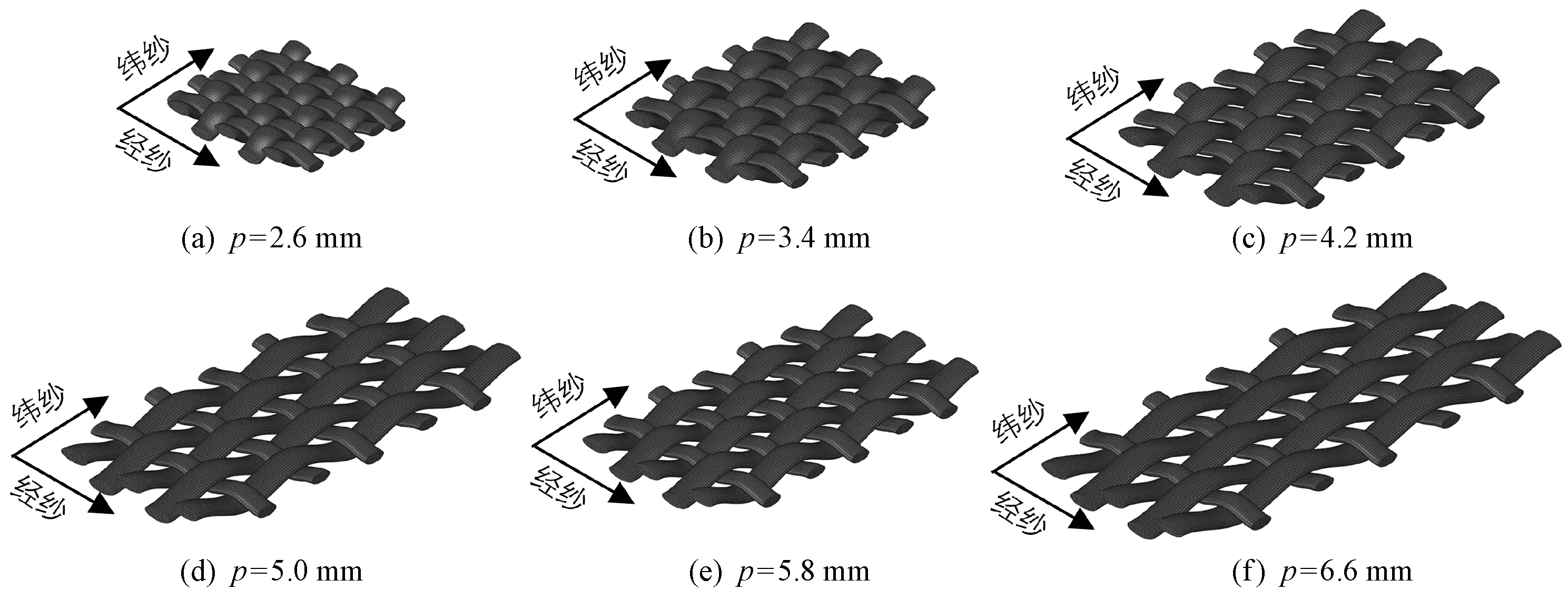
图10 经纱间距不同的平纹织物的3D模型Fig.10 Three dimensional-models of plain fabrics with different warp spacing

图11 经纱间距不同的斜纹织物的3D模型Fig.11 Three dimensional-models of twill fabrics with different warp spacing
2.2 有限元模拟
按照1.2所描述的方法对不同结构的织物进行纬向拉伸有限元模拟,根据图7显示的应力分布,以等效应力达到2 031.6 MPa作为计算终止的条件。
3 结果与分析
3.1 经纱间距对纬向拉伸性能的影响
根据表1织物增强层的结构参数,仅改变经纱间距,建立不同经纱间距的织物模型并对其进行纬向拉伸有限元模拟。图12为经纱间距p不同的织物纬向拉伸应力-应变曲线。可以看出,产生相同应变时,织物的纬向拉伸模量随经纱间距的增加而增加,并且逐渐接近单根纬纱拉伸的模量。其中,经纱间距在2.6~4.2 mm之间时,经纱间距的变化对织物的纬向拉伸模量影响较大,经纱间距在4.2~6.6 mm之间时,改变经纱间距,织物的纬向拉伸模量变化不大。

图12 经纱间距不同的织物纬向拉伸应力-应变曲线Fig.12 Stress-strain curves of fabrics with different warp spacing in weft tension. (a)Plain fabric;(b)Twill fabric
3.2 纬纱粗细对纬向拉伸性能的影响
根据表1织物增强层的结构参数,保持纬纱横截面长轴与短轴的比值为2.75,仅改变横截面短轴长度,建立了纬纱横截面短轴长度分别为1.0、0.8、0.6、0.4、0.2 mm的织物模型并对其进行了纬向拉伸有限元模拟。以横截面短轴长度t代表纬纱粗细,图13为纬纱粗细不同的织物纬向拉伸应力-应变曲线。可以看出,产生相同应变时,织物的纬向拉伸模量随纬纱变细而增加,并且逐渐接近单根纬纱拉伸的模量。纬纱横截面短轴长度在0.2~0.6 mm之间时,纬纱粗细的变化对织物的纬向拉伸模量影响较大,纬纱横截面短轴长度超过0.6 mm后,改变纬纱横截面短轴长度,织物的纬向拉伸模量变化不大。

图13 纬纱粗细不同的织物纬向拉伸应力-应变曲线Fig.13 Stress-strain curves of fabrics consist of weft with different thickness in weft tension.(a)Plain fabric;(b)Twill fabric
3.3 组织图案对纬向拉伸性能的影响
图14、15分别描绘了相同经纱间距和相同纬纱粗细的织物纬向拉伸应力-应变曲线。从中可以看出,相同结构参数的平纹和斜纹织物被拉伸至相同应变时,斜纹织物的纬向拉伸模量大于平纹织物;经纱间距处于4.2 ~6.6 mm之间时,平纹织物和斜纹织物的宏观力学响应差别明显,而经纱间距处于2.6~4.2 mm之间时,平纹织物和斜纹织物的宏观力学响应差别不大;纬纱横截面短轴长度处于0.6~1.0 mm之间时,平纹织物和斜纹织物的宏观力学响应差别明显,纬纱横截面短轴长度处于0.2~0.6 mm之间时,平纹织物和斜纹织物的宏观力学响应差别不大。
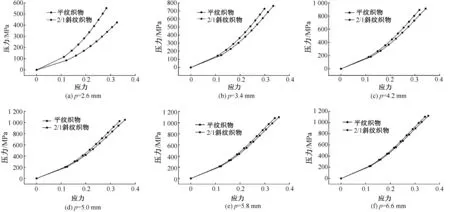
图14 经纱间距相同的平纹织物和斜纹织物纬向拉伸应力-应变曲线Fig.14 Stress-strain curves of plain and twill fabrics with the same warp spacing in weft tension.
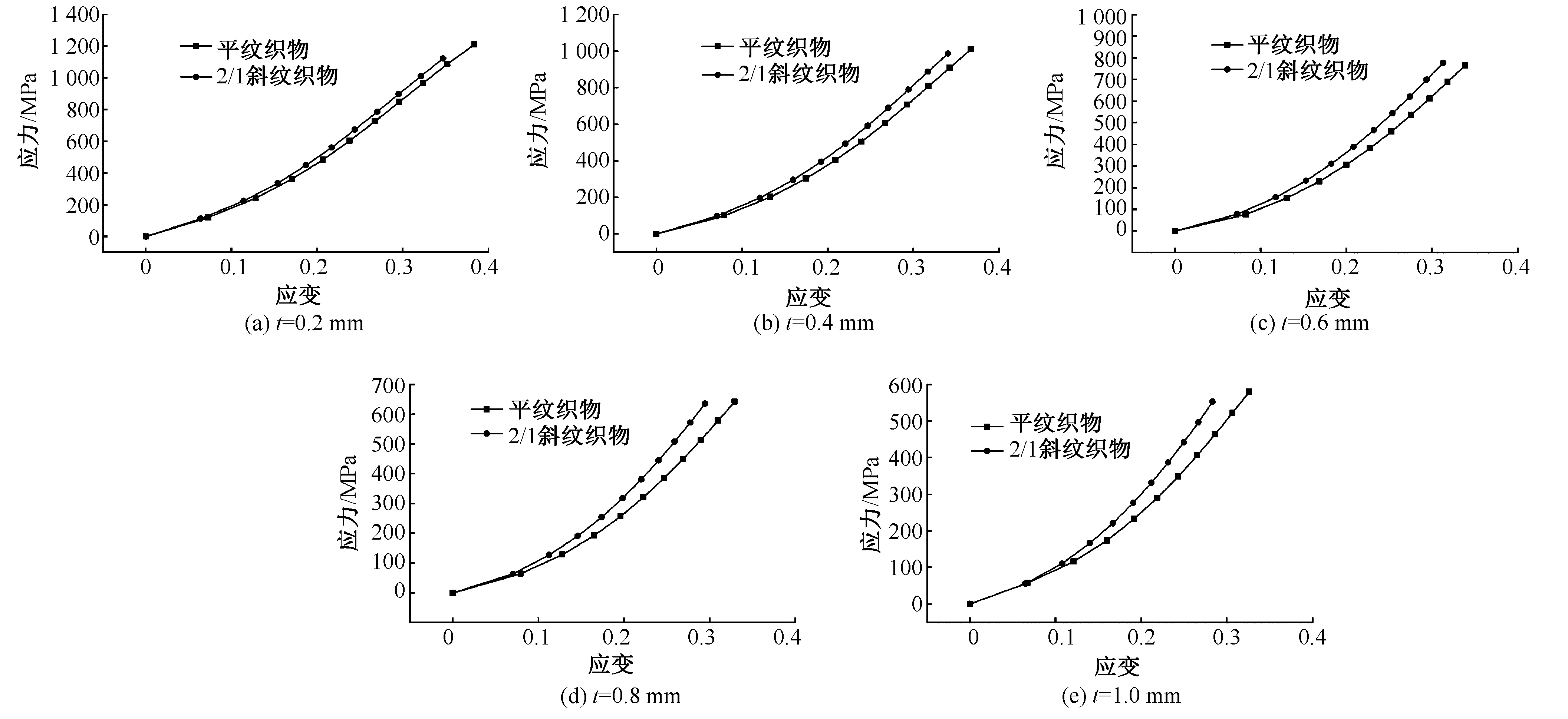
图15 纬纱粗细相同的平纹织物和斜纹织物纬向拉伸应力-应变曲线Fig.15 Stress-strain curves of plain and twill fabrics consist of weft with the same thickness in weft tension.
3.4 纬向织缩率对纬向拉伸性能的影响
以上分析表明,经纱间距、纬纱粗细和组织图案对织物的纬向拉伸性能具有重要影响,但是当织物的经纱间距或纬纱粗细处于不同大小区间时,改变经纱间距或纬纱粗细对织物纬向拉伸性能的影响却不同。为了探究导致这种现象的原因,对结构与织物拉伸性能的关系进行了进一步探讨。将织物的纬向织缩率(纬向织缩率=1-织物纬向长度/纬纱长度[13])列在表2中。可知,织物的经纱间距越长、纬纱越细则纬向织缩率越小,斜纹织物的纬向织缩率比平纹织物小;经纱间距越长、纬纱越细,平纹织物和斜纹织物的纬向织缩率越接近;在经纱间距处于2. 6~4.2 mm之间时,经纱间距的变化对纬向织缩率影响更大,纬纱横截面短轴长度处于0.2~0.6 mm之间时,纬纱粗细的变化对纬向织缩率的影响更大。结合图12~15可以看出,纬向织缩率越小,产生相同应变时,织物的纬向拉伸模量越大,越不容易拉伸变形;纬向织缩率越接近,织物纬向拉伸的宏观力学响应越相似。图16对比了纬向织缩率相同的织物纬向拉伸的应力-应变曲线,可以看出,这些织物的宏观力学响应完全一致。以上分析表明,纱间距、纱线粗细和组织图案共同决定了织物的织缩率,对于由相同纤维组成的织物,沿拉伸方向的织物织缩率决定了织物拉伸过程中的宏观力学响应。
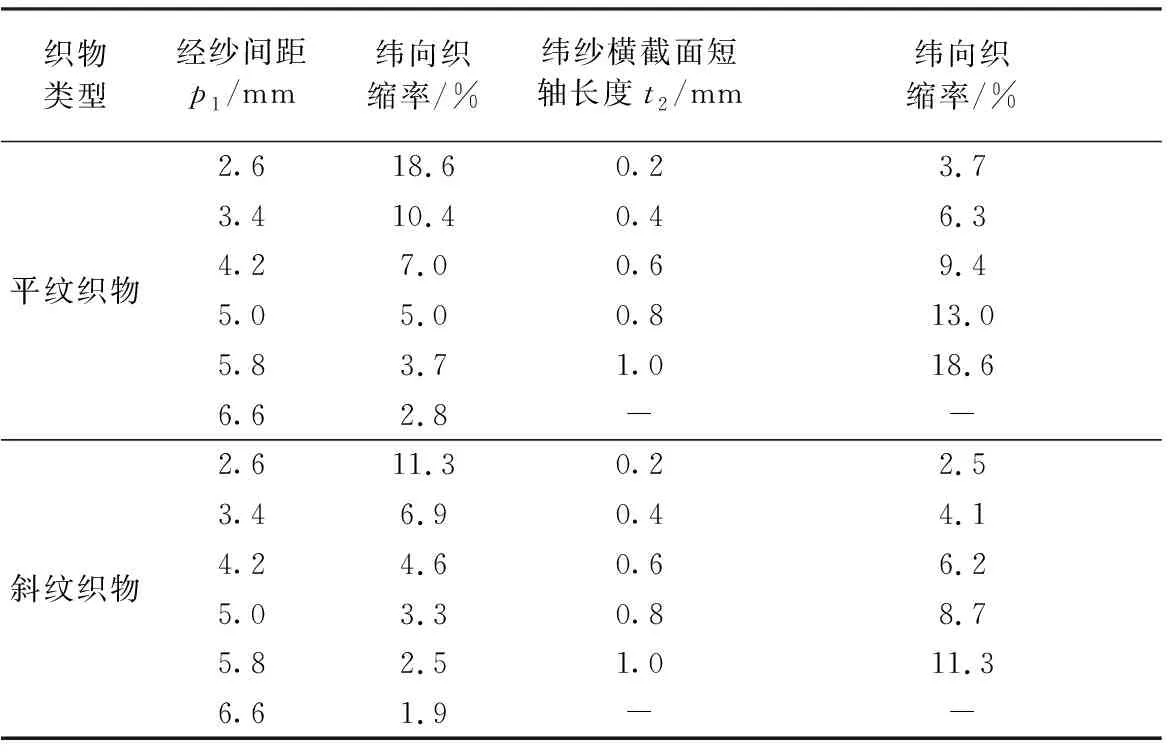
表2 织物纬向织缩率Tab.2 Weft weaving shrinkage of fabrics

图16 相同纬向织缩率的织物纬向拉伸应力-应变曲线Fig.16 Stress-strain curves of fabrics with the same weft crime rate weaving shrinkage in weft tension.(a)Plain fabrics with weft crime rate shrinkage of 37%;(b)Twill fabrics with weft crime rate shrinkage of 25%
4 织物结构对软管强度的影响
在实际应用中,单位体积纱线含量相同时,与单层平纹或斜纹织物相比,可扁平输送软管的增强层为双层斜纹织物时承压强度更高[14]。在输送液体的过程中,可扁平输送软管的承压强度会由于体积发生膨胀而降低,结合前面的分析可知,因为双层斜纹织物中的织物织缩率比单层平纹或斜纹织物小,拉伸模量更高,所以在承压输送过程中软管直径变化更小,承压强度更高。
5 结 论
本文通过对经纱间距在2.6~6.6 mm之间的平纹和斜纹织物以及纬纱横截面短轴长度在0.2~1.0 mm之间的平纹织物和斜纹织物进行纬向拉伸有限元模拟,探究了经纱间距、纬纱粗细、组织图案和纬向织缩率对织物拉伸性能的影响,分析了织物结构对可扁平输送软管承压强度的影响,得出如下结论。
①经纱间距越大,织物纬向拉伸模量越高,越不容易拉伸变形,经纱间距在2.6~4.2 mm时,经纱间距的变化对织物纬向拉伸模量的影响较明显。
②纬纱短轴长度越小,织物纬向拉伸模量越高,越不容易拉伸变形,纬纱短轴长度在0.2~0.6 mm之间时,纬纱粗细的变化对织物纬向拉伸模量的影响较明显。
③织物的纬向织缩率越小,则纬向拉伸模量越高,越不容易拉伸变形。织物的经纱间距越大,纬纱越细,则纬向织缩率越小。
④斜纹织物的拉伸模量高于平纹织物。经纱间距越小,纬纱越粗,纬向织缩率越大,平纹织物和斜纹织物拉伸模量的差异越明显。
⑤单位体积纱线含量相同时,双层斜纹织物的织物织缩率比单层平纹织物或斜纹织物的织物织缩率小,增强层为双层斜纹织物的可扁平输送软管在承压输送过程中直径变化更小,承压强度更高。

