微分求积法分析平面接头应力奇异性*
葛仁余,张佳宸,马国强,刘小双,牛忠荣
(1.安徽工程大学 力学重点实验室,安徽 芜湖 241000;2.合肥工业大学 土木与水利工程学院,合肥 230009)
引 言
不同材料的连接是机械工程和材料科学中经常遇到的一种情况.由于组成材料的弹性性质不同,连接点是产生结构破坏失效的薄弱部位和损伤源.结构在这些薄弱部位产生强应力集中,以至于在弹性力学意义上应力趋于无穷大,这种弹性力学范围内应力趋于无穷大的特性称为应力奇异性.当外载荷作用时,在结构的这些薄弱部位会产生很高的应力集中,会导致结构在V 形切口或接头连接点处出现龟裂等多种破坏形式.由于接头应力场的奇性指数对结构强度有决定性的影响,因此,获取奇性指数对确保结构服役的可靠性和安全性具有重要意义[1-2].
接头连接点处应力奇点研究方法有若干种,每种方法都有各自的特点,例如,Mellin 变换法是一种计算应力奇性指数简便而十分有效的方法[3-5].Williams[6](1952年)用直接的Airy 应力函数法研究了幂应力奇异性.England[7](1971年),Stern 和Soni[8](1976年),以及Carpenter 和Byers[9](1987年)使用了简单的复势方法来研究幂应力奇异性.Paggi 和Carpinteri[10]对含切口结构和多材料接头应力奇异性进行了广泛的研究,从数学上证明了特征函数展开法、复变函数法和Mellin 变换法在求解应力奇性指数方面的等价性.
为了确定和降低材料微观结构中的应力奇性指数,人们开始关注不同材料组成的接头结构的应力奇异性问题[11-13].例如,张金轮和葛仁余等[14]运用插值矩阵法分析了平面接头与界面裂纹的应力奇性指数;Sator等[15]从特征方程出发,获得了平面接头应力奇性指数实数解的精确值,用Newton 法获得了应力奇性指数复数解的数值解;在假设特征值为复数的前提下,Carpinteri 等[16]运用特征函数展开的方法研究了多材料连接点处的应力奇异性问题;Cho 等[17]利用复势方法以及复根的概念,研究了双材料V 形切口裂纹的幂对数应力奇异性问题.
1971年,Bellman 和Casti[18]提出了微分求积法(DQM)基本理论,在求解微分方程特征值和边值问题时,由于该理论不依赖于变分原理,具有公式简单、编程方便、高效、精度高等特点,是一种有吸引力的直接求解微分方程的数值计算方法,并且能以较少的网格点求得微分方程的高精度数值解,所以其在振动工程领域得到了广泛应用,主要用来求解工程结构的自由振动和强迫振动问题.本文创新性地将该方法运用到工程断裂力学的研究领域.根据弹性力学基本理论,将异质双材料平面接头连接点处应力奇性指数的计算转化为一组常微分方程组(ODEs)的特征值问题,再由DQM 基本理论将其转化为标准型广义代数方程组特征值问题,最后,一次性地计算出异质材料平面接头连接点处应力奇性指数及其相应的位移和应力特征函数.
1 平面接头应力奇性指数及其DQM 计算
图1为各向同性双材料平面接头模型,Γ1和 Γ3为 两自由楔边,Γ2为两种不同材料的交界边.在接头连接点O处同时定义一个直角坐标系xOy和 一个极坐标系rOθ,交界 Γ2与x轴重合,θ逆时针方向为正,顺时针方向为负.对于一个平面接头构件,基于Williams 渐近展开理论[6],将接头连接点处的位移场表达成关于径向r的级数渐近展开形式:
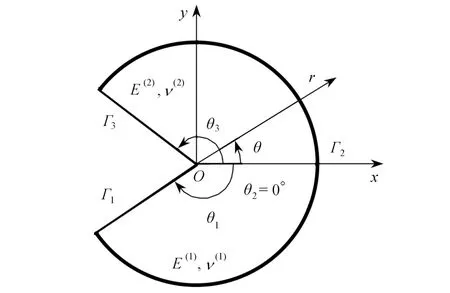
图1 两相材料平面接头模型Fig.1 The 2-phase isotropic multi-material junction model

关于平面应力问题,将式(1)代入各向同性材料本构方程,获得接头连接点处应力分量如下:

式(1)和(2)中,λk为应力奇性指数,Ak为位移幅值系数(k=1,2,3,···,M),M是截取的级数项数;上标m=1,2分别表示材料域1和材料域2,(θ)(i=r,θ)为相应材料域的径向和周向位移特征函数,(θ)(ij=rr,θθ,rθ)为相应材料域的应力特征函数,(θ)为(θ)的线性组合,即
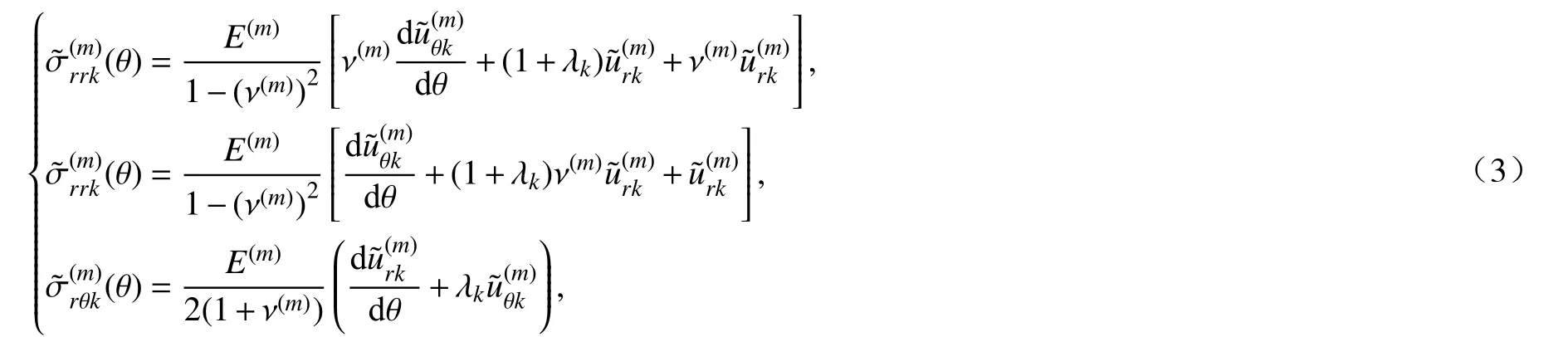
式中,E(m)和 ν(m)分 别为相应材料域的弹性模量和Poisson 比.考虑平面应变问题时,只需将式(3)中的E(m)用替换,用替换.在极坐标系下,无体力的弹性力学平面问题平衡方程为

为了便于编程计算,引入归一化变量ξ,0 ≤ξ≤1.在区间[θ1,θ2]中,归一化变量ξ 为

在区间[θ2,θ3]中,归一化变量ξ 为

将式(2)、(5)代入平面问题的平衡方程(4)中,得

其中,矩阵列向量L,M和N为(ξ),(ξ)及其第1 阶、第2 阶导数的线性组合(m=1,2),即
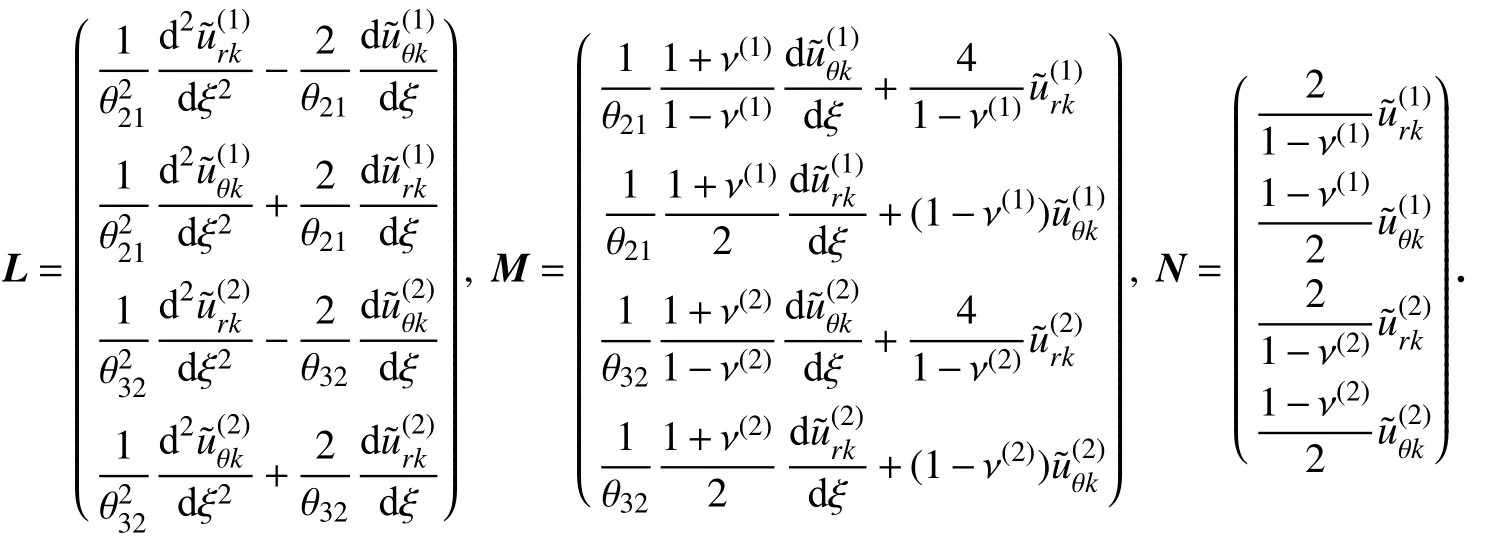
图1平面接头两自由楔边 Γ1和 Γ3上的面力为零,则边界条件可表示为


图1平面接头交界 Γ2上位移连续、面力相等,则交界条件可由下式表示:

至此,平面接头应力奇性指数的分析变成了求解在边界条件(7)和交界条件(8)下,ODEs(6)的特征值问题.这里,运用DQM 计算平面接头结构的应力奇性指数.图1平面接头的两个楔形圆弧区间θ1≤θ≤θ2和θ2≤θ≤θ3上的离散单元总数皆为N,离散节点总数皆为N+1,即,其中 ξ0=0,ξN=1.离散节点分布方式采用等步长均匀网格模式,即

DQM 的基本思想是:将归一化的位移特征函数(ξ),(ξ)(0 ≤ξ≤1)及其r阶导数在其求解域中任意离散节点上的近似值,表示为所有离散节点上值的线性加权和.即

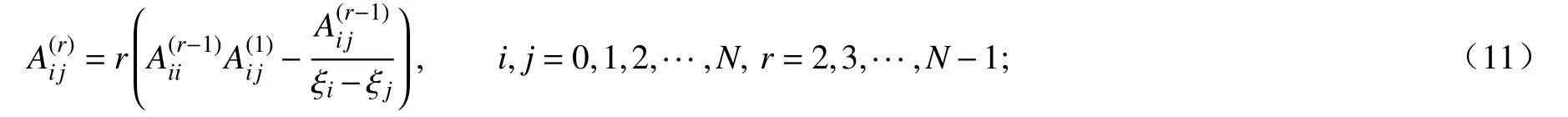
当i=j时,有
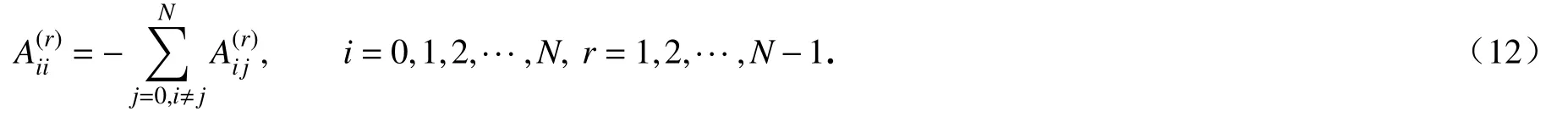

式中,R(1)为

将式(10)中表示的DQM 规则应用于ODEs(6),从而得到关于平面接头应力奇性指数 λk为特征值的一组代数方程组为

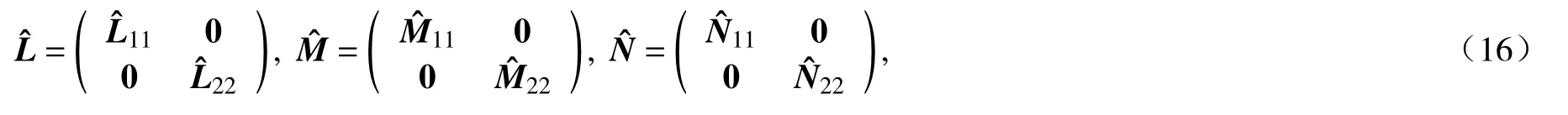
其中
最后,再将边界条件(7)和交界条件(8)中关于E(m)和 ν(m)的常系数表达式替换式(15)矩阵,和中相应的首行和末行.根据以上公式,笔者用FORTRAN 语言编写了通用程序DQMEI 用于DQM 计算平面接头应力奇性指数 λk及其相应的位移特征函数(θ)和 应力特征函数(θ).
2 数值算例及问题讨论
2.1 算例1:平面接头模型1
图2为平面接头模型1,α=180°是 一定值,β角是变化的.考虑平面应变情况,并且假定两种材料的Poisson 比ν(1)=ν(2)=0.2 ;离散单元总数分别取N=4,6,8,10,12,离散节点分布形式采用等步长均匀网格模式,运用DQM 求解ODEs(6)、边界条件(7)和交界条件(8),获得两相材料接头连接点处应力奇性指数随材料的弹性模量比值 η =E(2)/E(1)以及楔角 β 变化的计算值,如表1~3 所示.从表1~3 可知,在离散单元总数N=4 和N=6 时,DQM 计算值与实际值误差较大,随着N逐渐增加,DQM 计算值加速收敛.当N=12 时,DQM 计算值与文献[14]的计算结果至少有5 位有效数字相同,表明了本文数值方法计算平面接头应力奇性指数的有效性和精确性.

图2 平面接头模型1Fig.2 Plane junction model 1
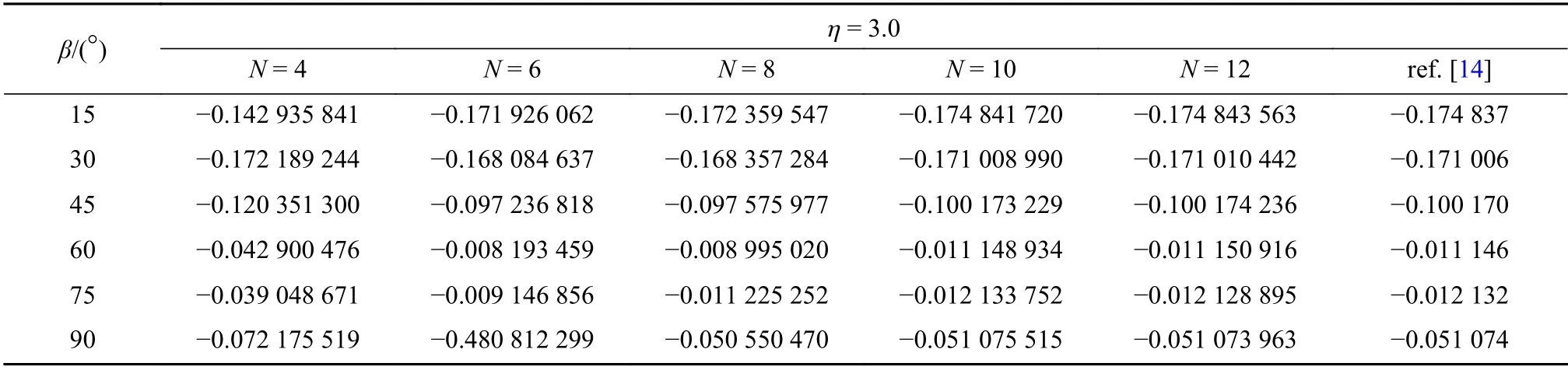
表1 η = 3.0 时,平面接头模型1 的第1 阶应力奇性指数λ1 计算值随离散单元数N 的变化Table 1 Variation of the 1st-order stress singularity index of plane joint model 1 with number of discrete elements N for η = 3.0
当 β=90°和 β=15°时,平面接头模型1 连接点处应力奇性指数随材料的弹性模量比值η =E(2)/E(1)的变化曲线如图3、4 所示.本文DQM 计算值与文献[15]的解析解及Newton 迭代法计算结果一致,同时,DQM 计算结果还表明:图3中,β=90°,0.001≤η≤10 000 时,接头仅存在一个实数奇性指数;图4中,β=15°,0.001<η≤1时,R e λ=0 平面接头模型1 连接点处无应力奇异性,1 <η≤511.9时,连接点处存在1 个实数奇性指数,5 11.9<η≤851.3时,连接点处存在2 个实数奇性指数,尤其当 8 51.3<η≤10 000时,由于材料的相互不匹配性,平面接头模型1 连接点附近区域应力奇性指数是复数,而不是实数,产生振荡应力奇异性[23].
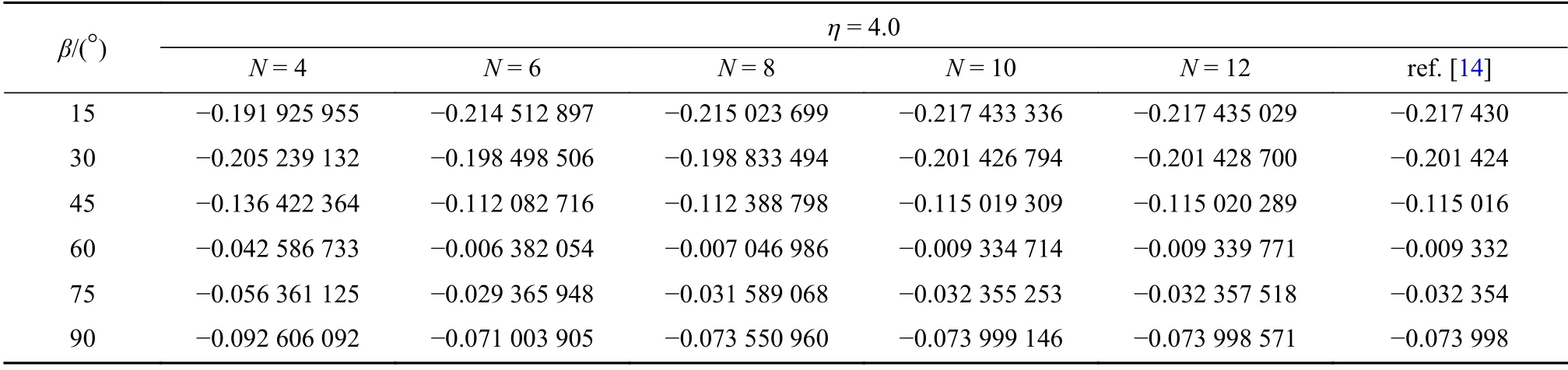
表2 η = 4.0 时,平面接头模型1 的第1 阶应力奇性指数λ1 计算值随离散单元数N 的变化Table 2 Variation of the 1st-order stress singularity index of plane joint model 1 with number of discrete elements N for η = 4.0
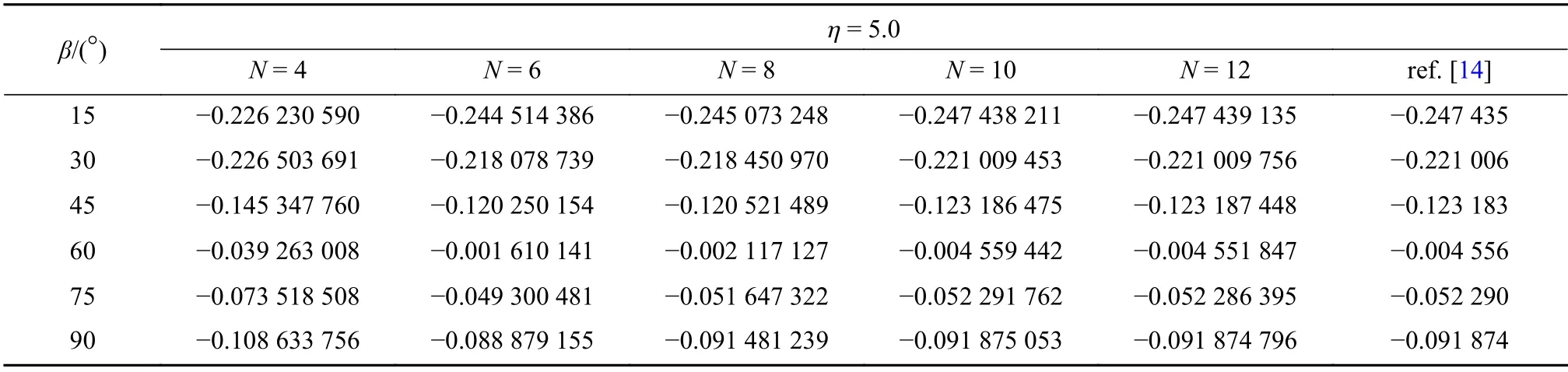
表3 η = 5.0 时,平面接头模型1 的第1 阶应力奇性指数λ1 计算值随离散单元数N 的变化Table 3 Variation of the 1st-order stress singularity index of plane joint model 1 with number of discrete elements N for η = 5.0
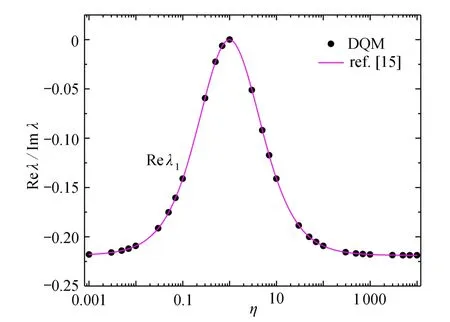
图3 当β = 90°时,平面接头模型1 的应力奇性指数Fig.3 The singular index of stress in plane joint model 1 for β = 90°
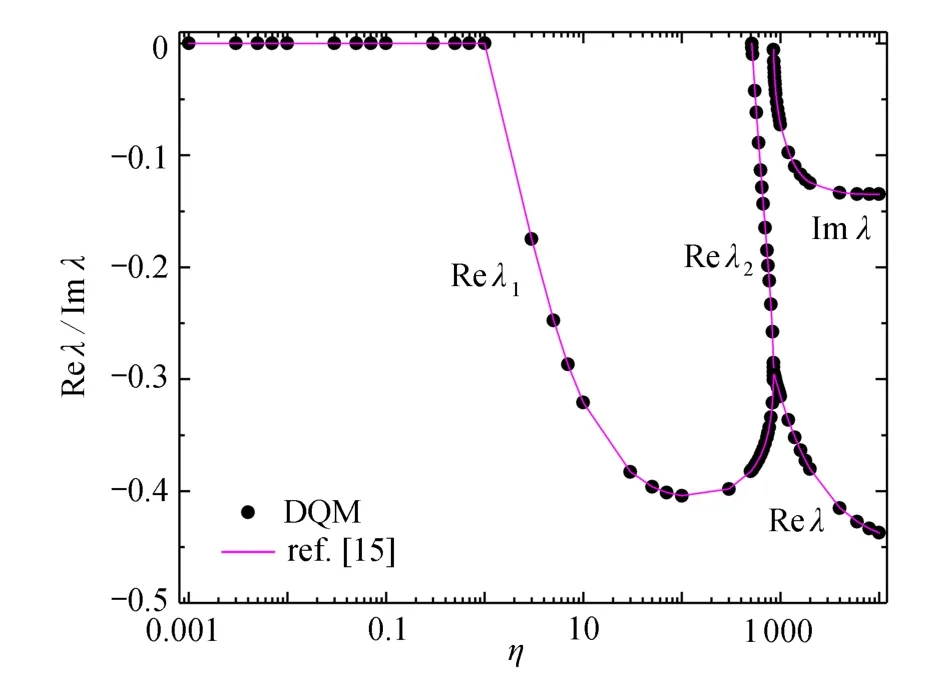
图4 当β = 15°时,平面接头模型1 的应力奇性指数Fig.4 The singular index of stress in plane joint model 1 for β = 15°
图2中,在平面应变条件下,当 β=90°、离散单元总数N=12 时,在η =E(2)/E(1)=0.01和 η =E(2)/E(1)=0.1两种情况下,由本文DQM 获得连接点处的第1 阶应力奇性指数分别为 λ1=−0.209 247 37、 λ1=−0.141 009 68,它们对应的位移特征函数和应力特征函数分布曲线如图5、6 所示.从计算结果中看出,位移分量和在粘接界面上虽然连续,位移特征函数曲线却出现转折,两种材料的弹性模量相差越大,转折越明显,而且,径向应力特征函数在粘接界面上出现突变,弹性模量相差越大突变越激烈,这就是接头连接点处发生开裂破坏的 主要原因.但是,另外两个应力特征函数和在粘接界面上连续,无明显的转折.

图5 E(2)/E(1) = 0.01 时,平面接头模型1 第1 阶应力奇性指数λ1 对应的位移和应力特征函数曲线图Fig.5 Displacement and stress characteristic function curves corresponding to 1st-order stress singular index λ1 of plane joint model 1 for E(2)/E(1) = 0.01
2.2 算例2:平面接头模型2
图7为平面接头模型2,设交界面两侧分属不同的均质弹性体材料,材料Poisson 比为ν(1)=ν(2)=0.2;α=180°是一定值,β角是变化的.在平面应变条件下,两个区间 [−α,0°]和[0°,β]上离散单元总数取N=12时,由DQM 计算获得以下结论:① 如图8所示,当 β=180°时,平面接头模型2 退化为双材料界面裂纹模型,当0.001≤η≤10 000 时,界面裂纹尖端应力奇性指数是一对复数,实部值 Re λ=−0.5,虚部值 Im λ很小.② 如图9所示,当 β=135°和 0 .17<η<2.82 时,平面接头连接点处应力场存在2 个实数奇性指数;当 0 .001≤η≤0.17和2.82≤η≤10 000时,平面接头连接点处为2 个复数奇性指数,产生振荡应力奇异性[23].根据图8、9 可知,本文DQM 计算值与文献[15]计算结果一致,再次证明本文DQM 对分析一般平面接头应力奇性指数是一种有效且准确的手段.
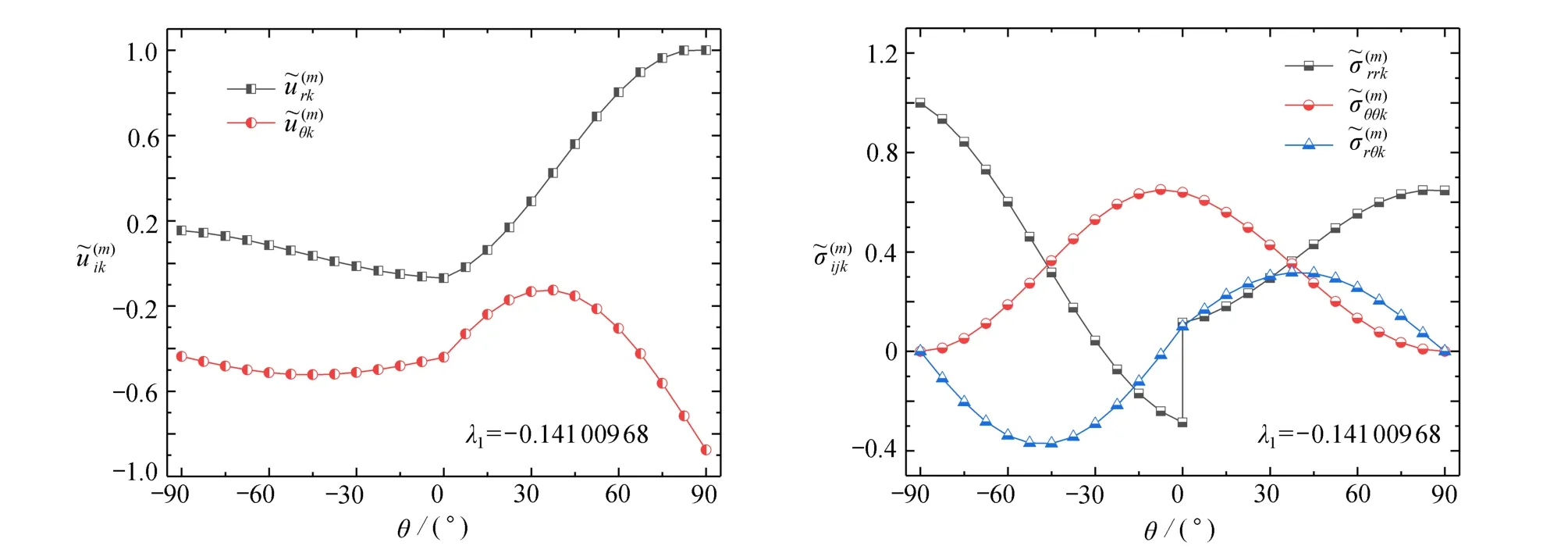
图6 E(2)/E(1) = 0.1 时,平面接头模型1 第1 阶应力奇性指数λ1 对应的位移和应力特征函数曲线图Fig.6 Displacement and stress characteristic function curves corresponding to the 1st-order stress singular index λ1 of plane joint model 1 for E(2)/E(1) = 0.1
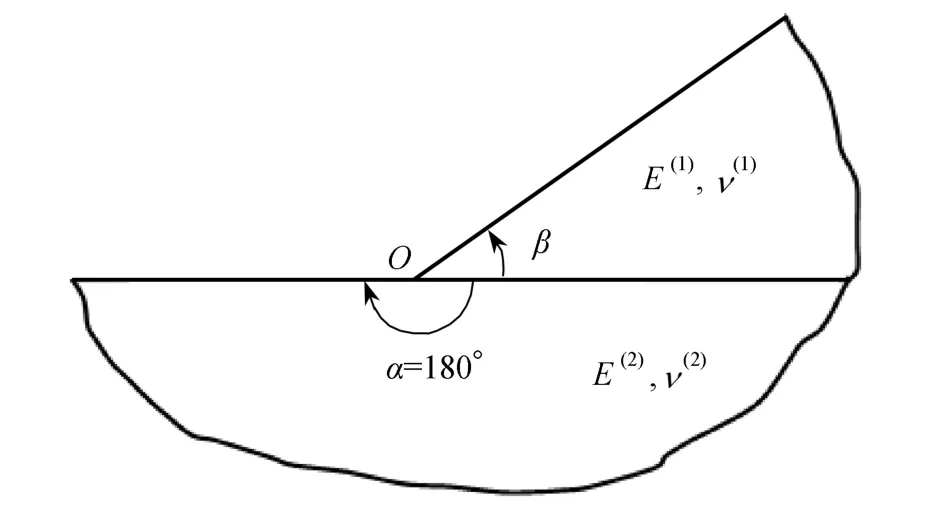
图7 平面接头模型2Fig.7 Plane junction model 2
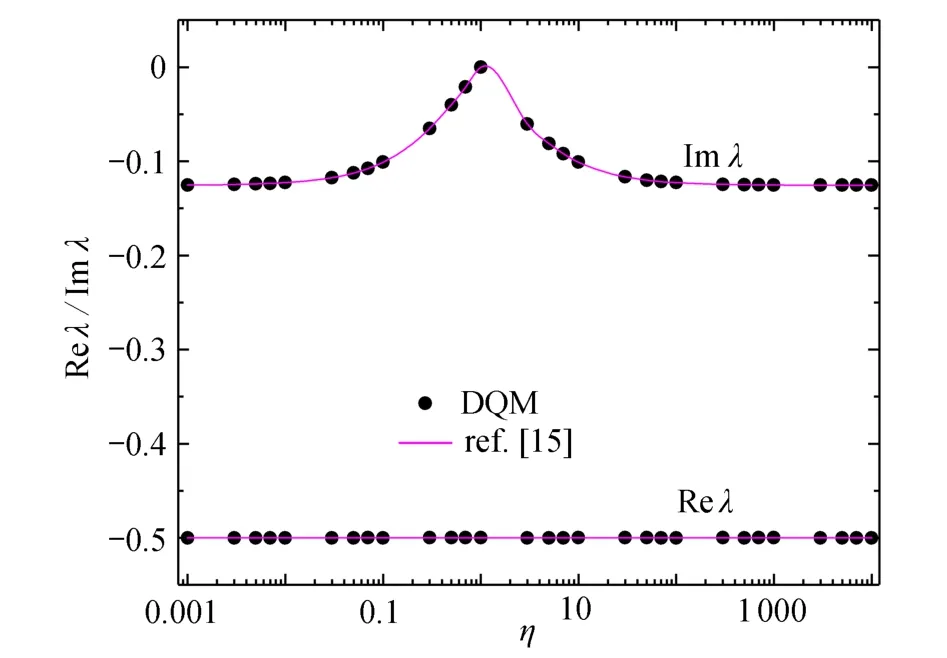
图8 当β = 180°时,平面接头模型2 应力奇性指数Fig.8 The singular index of stress in plane joint model 2 for β = 180°
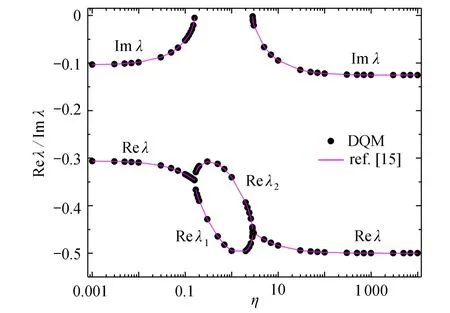
图9 当β = 135°时,平面接头模型2 应力奇性指数Fig.9 The singular index of stress in plane joint model 2 for β = 135°
图7中,在平面应变条件下,当 β=90°,η =E(2)/E(1)=3时,由本文DQM 计算获得平面接头的前2 阶应力奇性指数分别为 λ1=−0.498 701 52和 λ2=−0.222 442 62,它们对应的位移和应力特征函数分布曲线如图10、11 所示.从图11 中看出,第2 阶应力奇性指数 λ2对 应的位移特征函数分布曲线和在粘接界面上连续且转折,径向应力特征函数分布曲线在粘接界面上出现突变,与图10 第1 阶应力奇性指数 λ1对应的特征函数曲线分布规律一致.

图10 E(2)/E(1) = 3 时,平面接头模型2 第1 阶应力奇性指数λ1 对应的位移和应力特征函数曲线图Fig.10 Displacement and stress characteristic function curves corresponding to the 1st-order stress singular index λ1 of plane joint model 2 for E(2)/E(1) = 3
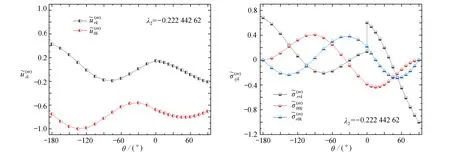
图11 E(2)/E(1)=3 时,平面接头模型2 第2 阶应力奇性指数λ2 对应的位移和应力特征函数曲线图Fig.11 Displacement and stress characteristic function curves corresponding to the 2nd-order stress singular index λ2 of plane joint model 2 for E(2)/E(1)=3
2.3 算例3:平面接头模型3
图12 为两个材料完全粘接在一起的平面接头模型3,其中材料1 和材料2 均为各向同性材料,材料Poisson 比为 ν(1)=ν(2)=0.2,α=270°,β=90°.在每个材料域上离散单元总数皆取N=12 时,图13 给出了η=E(2)/E(1)从0.001 至10 000 时,DQM 计算的应力奇性指数的变化曲线,表明了两相材料属性关系对奇异性应力状况的影响情况,本文计算值与文献[16]的结果完全一致.
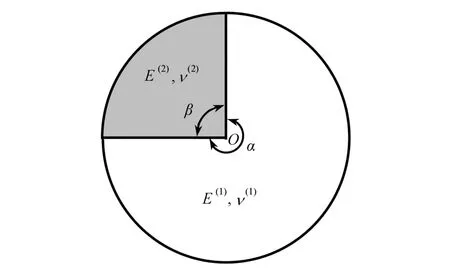
图12 平面接头模型3Fig.12 Plane junction model 3
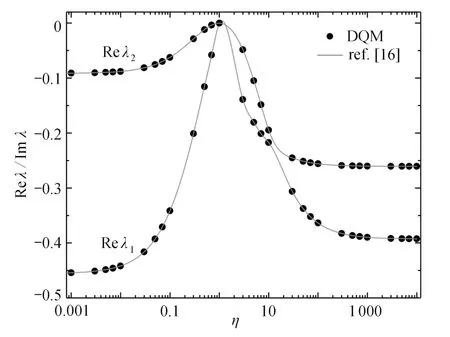
图13 当β = 90°时,平面接头模型3 应力奇性指数Fig.13 The singular index of stress in plane joint model 3 for β = 90°
3 结 论
DQM 在振动工程领域应用比较广泛,主要用来求解结构的自然频率及振型,本文创新性地将该法运用到弹性力学和工程断裂力学的研究领域.基于平面接头连接点处位移场和应力场的Williams 渐近展开式,将其典型项代入平面问题平衡方程中,将平面接头的线弹性理论微分方程转换成一类ODEs 特征值问题,根据DQM 理论的计算列式,用 FORTRAN 编制了一个新求解器DQMEI 用于求解一般ODEs 特征值问题.最后应用DQMEI 分析了平面接头的应力奇性指数,同时,也一并求出了平面接头连接点处对应的位移和应力特征函数,这些特征函数在分析平面接头完整应力场和应力强度因子时是不可或缺的物理量.文中给出数值算例的DQM 计算值与已有文献结果完全一致,证明了求解一般平面接头连接点处应力奇性指数时,DQM 是一种有效且准确的手段.

