基于深度学习与SAE 网络的火箭推力下降故障诊断

陈海鹏， 闫 杰， 符文星

（西北工业大学无人系统研究院， 西安 710072）

1 引言

推力下降故障为运载火箭典型非致命动力系统故障类型，因此，及时的故障诊断能够及时预警，为后续的控制提供更有效的分配策略，避免任务的失败。 传统的故障诊断方法多基于模型实现，对解析模型的依赖较大，实际应用中建模的精确度高低是故障诊断准确与否的关键。 运载火箭本身是一个高复杂度的非线性系统，难以精确建模，即使精确建模也难以直接在卡尔曼滤波器法、鲁棒观测器法等方法中应用，需要进一步简化，且这一过程又会带来一定程度的误差。

基于知识的方法可以避免被控对象建立精确模型困难的问题，又能充分利用诊断对象特性的信息。 深度学习作为一种能够深度提取数据特征的方法，在故障诊断领域具有较大潜力。 基于深度置信网络（Deep Belief Network，DBN）的故障诊断适用于分类器以及特征的提取与识别。 蒋丽英等将主元分析与DBN 结合，用于航空发动机气路系统故障诊断，并利用实测数据验证该方法的准确性；Yang 等提出了一种基于改进DBN 的故障诊断方法，摆脱了传统机器学习方法对样本特征提取的依赖，有效克服了梯度消失、局部极值等问题，应用于滚动轴承数据的实验中。 基于卷积神经网络（Convolutional Neural Network，CNN）的故障诊断更适合处理大型数据，从中获取与故障相关的信息。 Gu 等提出了一种基于时间模态特征提取的经验模式分解变换方法，与结合卷积神经网络，应用于轴承故障诊断中；Xie 等提出了一种基于离散小波变换和卷积神经网络的滚动轴承故障诊断特征提取新方法，CNN所提取的特征反映原始信号的特征，并被训练成Softmax 分类器，用于旋转机械故障诊断。与DBN、CNN 相比，堆栈自编码器（Stacked Au⁃toencoder，SAE）能够在相对少的样本数据下，结合特征提取与分类技术实现较优的故障诊断结 果。 Pang 等提 出 了 一 种 基 于 优 化结构的多隐层极限学习机的航空燃气轮机气路部件故障诊断方法，应用于手写识别数据集和燃气轮机诊断应用；Wang 等提出了一种堆栈监督自动编码器来对深度网络进行预训练，并从原始输入数据中获取深度故障相关特征，提高了分类器的分类精度。

目前还未有研究将基于深度学习的方法用于运载火箭推力下降的故障诊断中，本文利用运载火箭运动学模型，生成样本数据，采用堆栈自编码器训练网络，对推力下降故障进行检测与估计，并通过数字仿真验证在线故障诊断效果。

2 数学模型

考虑运载火箭飞行过程中受到的气动力、控制力、推力、引力及附加力，在发射坐标系下建立运载器的质心运动方程如式（1）所示。

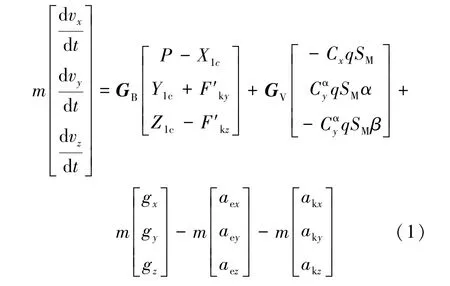
式中，为火箭质量，v、v、v为发射坐标系下各轴速度分量，为发动机推力，、、为滚转通道、偏航通道、俯仰通道的控制力，′、′为箭体坐标系下偏航、俯仰通道的附加哥氏力，C为运载火箭轴向力系数，为法向力系数对攻角的偏导，为当前飞行条件下的动压，为运载火箭最大横截面积，为攻角，为侧滑角，g、g、g为引力加速度各轴的分量，、、为离心惯性加速度各轴的分量，、、为哥氏惯性加速度各轴分量，为箭体系到发射系的坐标转换矩阵，为速度系到发射系的坐标转换矩阵。

质心动力学运动方程如式（2）所示。

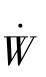
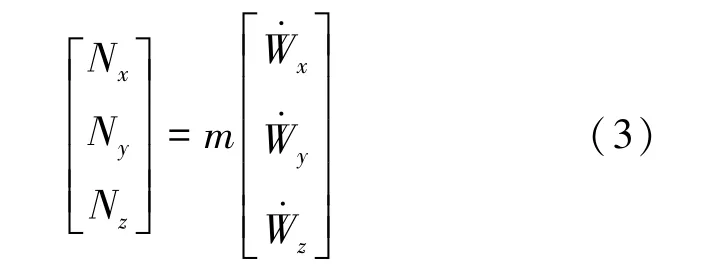
将过载与运载器质量及重力加速度乘积的比值定义为过载系数，如式（4）所示。

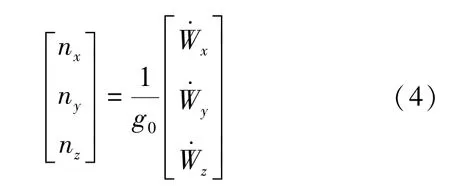
式中，n为轴向过载系数，n为法向过载系数，n为横向过载系数。

3 堆栈自编码器

自编码器（Autoencoder，AE）本质为一个单隐含层的神经元网络，属于无监督学习算法的一种，包含编码与解码2 个过程。 目的是通过寻求最优的权重与偏差参数，使得输出尽可能地重构输入，因此每次训练需要在获得输出时将误差反向传播，以优化输出结果。 编码过程数据维度不断降低，解码过程数据维度逐渐恢复，因而输出可视为输入降维后的低维特征。 图1 为自编码器示意图。

图1 自编码器示意图Fig.1 Schematic diagram of the autoencoder

单个自编码器包含输入层， 维数为， 隐含层，维数为；输出层＾，维数为。 选择sig⁃moid 函数作为神经元激活函数。

编码过程中，利用激活函数() 将输入投影到隐含层，公式如式（5）所示。

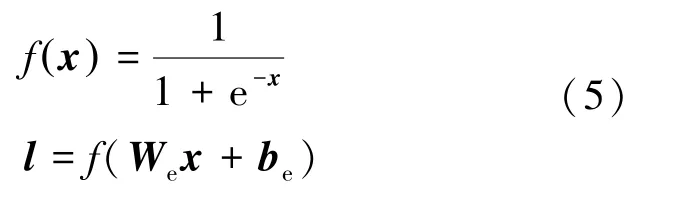
式中，为输入层到隐含层权重矩阵，维数为×；为偏差向量，维数为。

解码过程中，利用映射函数() 将隐含层投影到输出层，公式如式（6）所示。

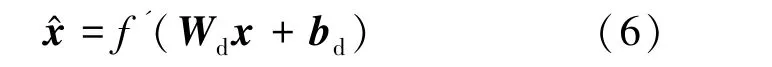
式中，为隐含层到输出层权重矩阵，维数为×；为偏差向量，维数为。

根据上述2 个过程，每个训练样本x都被投影到隐含层表示l， 然后被映射到重构数据＾。为了获得参数、、、，采用均方重构误差最小化的计算方式来重构误差损失函数，如式（7）所示。

式中，为训练样本总数。 自编码器采用梯度下降法训练网络参数，使损失函数（7）最小化。

堆栈自编码器包含无监督预训练过程和有监督微调训练过程。 堆栈自编码器由多层自编码器组成，预训练过程中，从第一层开始，每个AE 单独训练，目的是使输入输出间的误差最小，每一层AE 训练后的输出作为其下一层AE 的输入，继续训练下一层，直至训练到最后一层。 监督微调过程中，SAE 的初始权重与偏差值取预训练过程获得的输入层与隐层之间的权重和偏差。 使用BP算法计算各层误差，并使用梯度下降法完成各层权重和偏置的调节。

4 故障诊断

运载火箭动力系统发动机发生故障后，运载火箭推力表示如式（8）所示。

式中，为正常情况下推力， P为故障后推力，为推力下降程度，∈［0，1） 。

堆栈自编码器学习网络的输入样本应包含运载火箭推力下降故障的特征。 在可获取的运载火箭外部信息中，推力变化直接影响过载的变化，因此利用过载n、n信息作为网络的输入。 样本包含故障时刻与故障程度信息。 以0.5 s 为时间间隔、10%为推力下降间隔，存储每次六自由度模型仿真的弹道过载信息，作为样本数据，不同故障时刻下故障特征在样本中得以体现。

SAE 网络用于推力下降故障诊断的过程分为以下5 步：

1）获取运行器不同时刻、不同推力下降程度的过载信号，作为网络输入；

2）确定训练网络的层数、学习率、迭代次数以及各层的节点数；

3）逐层训练AE 网络，得到训练好的特征编码，用于网络微调环节；

4）微调整个网络，对网络准确率进行判断，如果准确率满足要求，即结束训练，否则从第3 步重复训练；

5）训练好的网络在仿真模型中实时调用，针对实时过载信息进行前向训练，根据训练结果判断故障的发生及推力下降程度的大小。

运载火箭推力下降故障诊断的流程如图2所示。

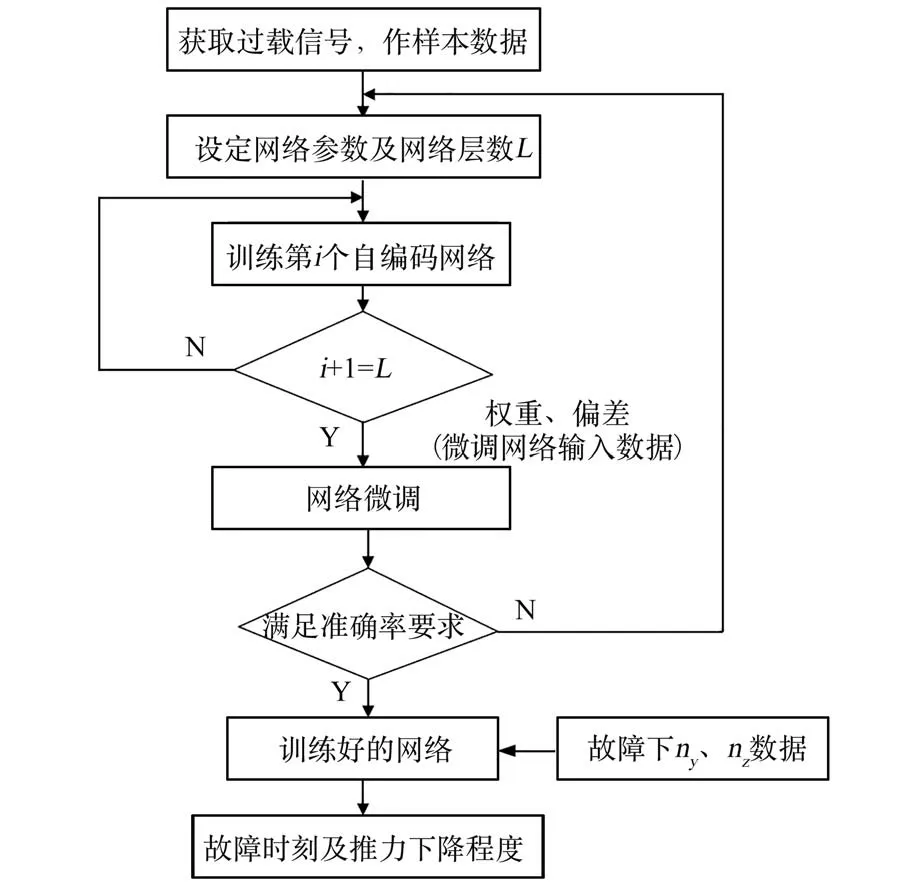
图2 动力系统推力下降SAE 网络训练及故障诊断流程图Fig.2 Flowchart of SAE network training and fault diagnosis for power train thrust drop

5 仿真验证

输入数据包含弹道的状态数据与标签数据。训练样本包含故障，并非利用重构误差。 数据标签为不同推力下降程度，范围为0 ～1，如发生30%的推力下降，标签记为0.7。

5.1 网络层数

设运载火箭30 s 发生30%推力下降故障，保持相同的学习率，每层隐含层设置节点数100，分别对包含3 层、4 层、5 层、6 层隐含层的SAE 网络进行训练，并用于故障诊断，经过多次训练，测试错误率如表1 所示。 可以看出，网络层数对训练结果的影响较小，为简化计算，缩短计算时间，选用3 层网络（即1 层隐含层）即可。

表1 不同网络层数下的故障诊断结果Table 1 Fault diagnosis results of different network layers

5.2 隐含层节点数

设运载火箭30 s 发生30%的推力下降故障，以10 个节点为间隔，分别对10 ～300 隐含层节点数下的网络进行故障诊断仿真。 将每次的测试错误率存储并绘制成曲线，如图3 所示。 可以看到，节点数小于160 时，测试错误率处于平稳小值水平，且足够节点数保证错误率最小，因此本次仿真采用100 节点数。

图3 不同隐含层节点下的测试错误率Fig.3 Test error rate under different hidden layer nodes

5.3 学习率

在合适的学习率区间内，损失函数会突降，过小的学习率导致损失函数减小速度缓慢，过大的学习率导致损失函数震荡甚至发散。 因此，最好的学习速率对应损失函数下降曲线最陡峭的部分。 为分析损失函数下降曲线的坡度，图4 给出了学习率与损失函数的关系曲线。 可以看出，坡度最抖的区域在0.2 以内，随着学习率继续增大，损失函数不断震荡最后发散。 因此将学习率设置为0.1。

图4 学习率与损失函数的关系曲线Fig.4 Relationship between learning rate and loss function

5.4 离线仿真验证

后续仿真中，深度学习网络设置为3 层，隐含层节点数为100，学习率设置为0.1。 无故障情况下的诊断结果理论上为标准值1，利用本文方法的诊断结果如图5 所示。 由图可见，无故障情况下诊断结果与标准值1 非常接近，误差在10以内，因此可将检测结果小于10的诊断值视为无故障发生。

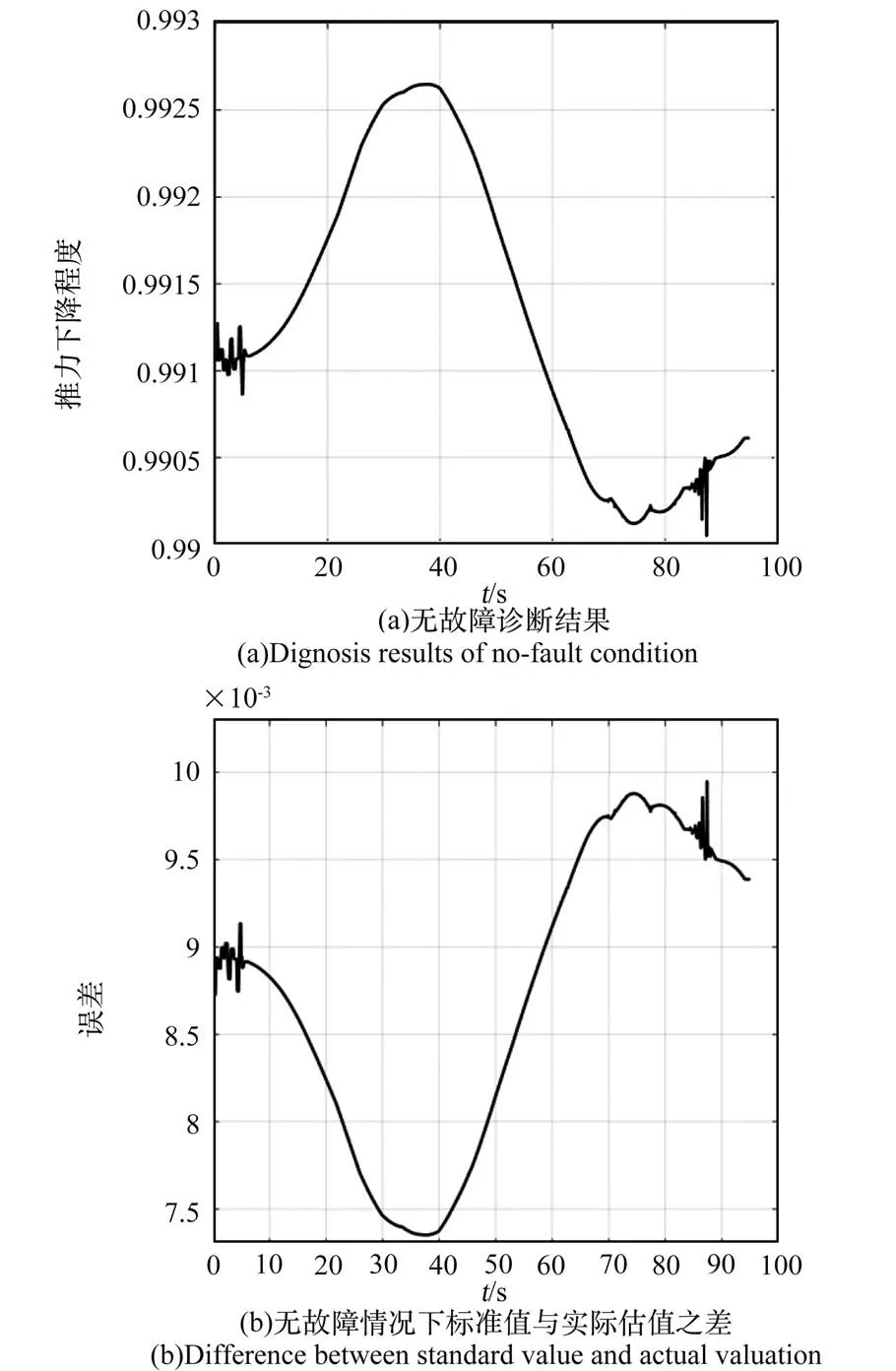
图5 无故障情况诊断结果Fig.5 Diagnosis results of no⁃fault condition

同一推力下降程度（下降30%）不同时刻的外部过载情况如图6 所示，普通神经网络方法与深度学习及SAE 网络方法诊断结果如图7 所示。

图6 30%推力下降下不同时刻的外部过载Fig.6 Overload of 30%thrust drop at different times

图7 可得，同一推力下降故障下，不同时刻的故障能够被准确检测。 与普通神经网络方法诊断结果相比，该方法更加平滑，且推力下降程度较普通神经网络法精确20%。 两种方法均可检测出非因推力故障所引起的过载突变，新方法受该突变影响较小，神经网络方法对该突变较为敏感，检测到的推力下降程度处于波动状态。

图7 30%推力下降下不同时刻故障的诊断结果Fig.7 Diagnosis results of 30% thrust drop fault at different times

同一时刻（20 s）不同程度推力下降的外部过载情况如图8 所示，其诊断结果如图9 所示。

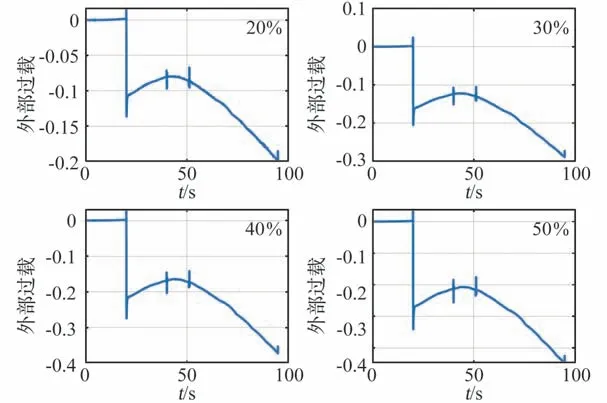
图8 20 s 下不同程度推力下降的外部过载Fig.8 Overload of different thrust drop at 20 s

图9 20 s 下不同程度推力下降故障的诊断结果Fig.9 Diagnossis results of different degrees of thrust drop at 20 s

图9 可得，故障发生后，推力下降程度有一个大于给定推力下降程度的突变，并在较短时间内达到接近给定的推力下降程度值，因此能够实现对不同推力下降程度的估计。 不同推力下降程度下，2 种方法均能对故障情况进行检测，随着故障程度增加，普通神经网络的诊断结果存在较大波动，说明深度学习SAE 网络能更好地适应推力下降程度较大的情况。

5.5 在线仿真验证

将训练好的网络加载到弹道中实时调用，随机时刻和随机程度推力下降的外部过载情况如图10 所示，其诊断结果如图11 所示。

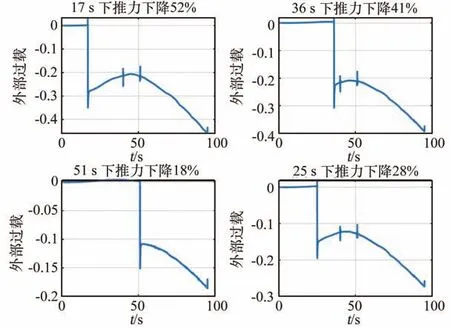
图10 随机时刻及随机程度推力下降的外部过载Fig.10 Overload of random time and random thrust drop

图11 随机时刻及随机程度推力下降故障的诊断结果Fig. 11 Diagnossis results of random time and random thrust drop fault

由于训练样本以10%的推力下降程度为间隔，且本文采用的自编码网络目的是使输出接近输入，因此在线仿真中，设定随机推力下降故障的诊断结果存在一定误差。 在此误差范围内，能够实现故障的判断以及推力下降程度的诊断。 故障时刻越滞后，普通神经网络方法对于故障程度的诊断误差越大，故障程度越大，诊断结果的波动更加明显，而深度学习SAE 网络则能更好地适应以上2 种情况，能够在多种故障条件下完成对故障的精确检测。

6 结论

本文实现了仿真条件下对运载火箭推力下降故障的辨别以及推力下降程度的准确估计，并结合离线与在线2 种方式验证了该方法的可行性：

1）离线仿真中，推力下降程度有一个大于给定推力下降程度的突变，并在较短时间内达到接近给定的推力下降程度值。

2）在线仿真中，设定随机推力下降故障的诊断结果存在一定误差。 故障时刻越滞后，普通神经网络方法对于故障程度的诊断误差越大，故障程度越大，诊断结果的波动更加明显，而深度学习SAE 网络则能更好地适应以上2 种情况，在此误差范围内，能够实现故障的判断以及推力下降程度的诊断。

3）不同推力与时刻的下降故障能够被准确检测。 与普通神经网络方法诊断结果相比，该方法精度提升20%，且更加平滑。