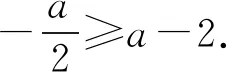从2021、2020两年高考试题看不等式选讲解题方略

游少华

(贵州省遵义市第四中学 563000)

课标卷中的两道选作题，学生如何选择，如何解答非常重要，甚至决定学生考试的成败.这两道题都体现数学的核心素养——数形结合的思想.但对不等式而言，无论是有变量问题还是定量不等式问题，学生都习惯分类讨论求解.分类讨论除分类不清外，还存在求交集错误问题，不等关系其本质上是函数图象的上下关系.如果能作图象解不等式，不但直观展现大小关系，更能方便看出不等关系的变量范围.

2021年与2020年两年的考题都体现这一解题思想.

题1 (2021年全国文理甲卷)已知函数f(x)=|x-2|,g(x)=|2x+3|-|2x-1|．

(1)在图1中画出y=f(x)和y=g(x)的图象；

(2)若f(x+a)≥g(x)，求a的取值范围．

图2

g(x)=|2x+3|-|2x-1|

画出函数图象如图3：

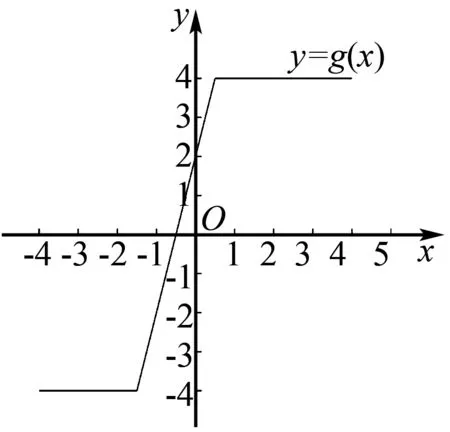
图3

(2)f(x+a)=|x+a-2|，

如图4，在同一个坐标系里画出f(x),g(x)图象，

图4

y=f(x+a)是y=f(x)平移了|a|个单位得到，

则要使f(x+a)≥g(x)，需将y=f(x)向左平移，即a>0.

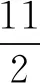
题2(2020年全国文理Ⅰ卷)已知函数f(x)=|3x+1|-2|x-1|．

(1)在图5中画出y=f(x)的图象；

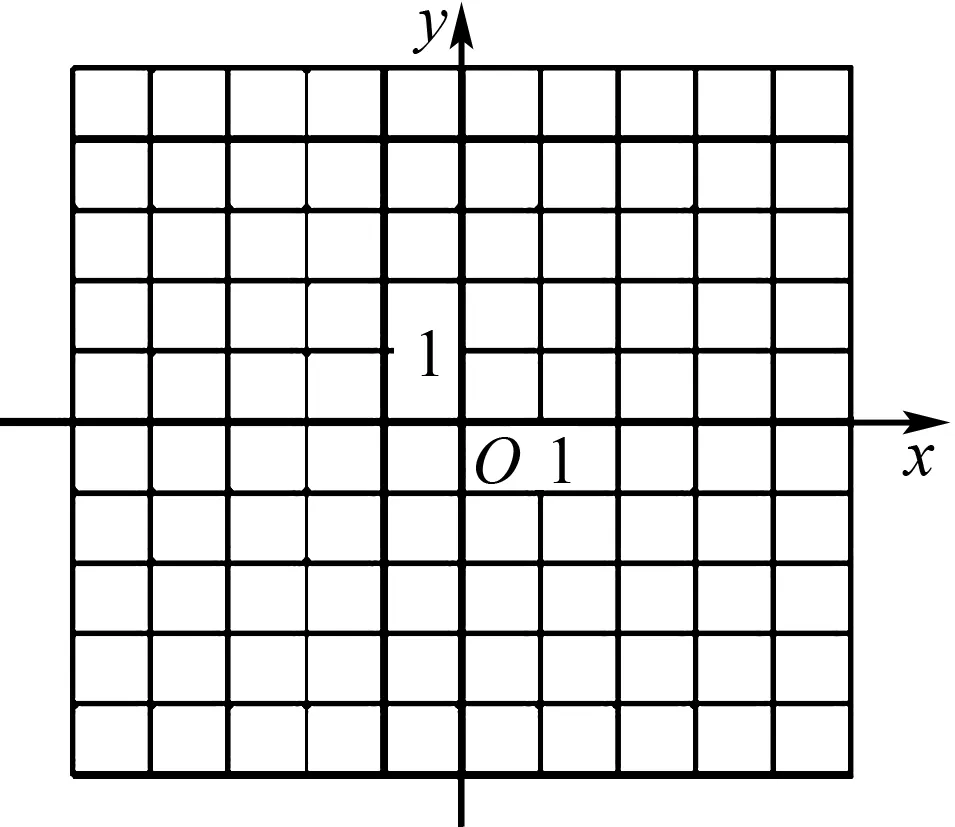
图5

(2)求不等式f(x)>f(x+1)的解集．

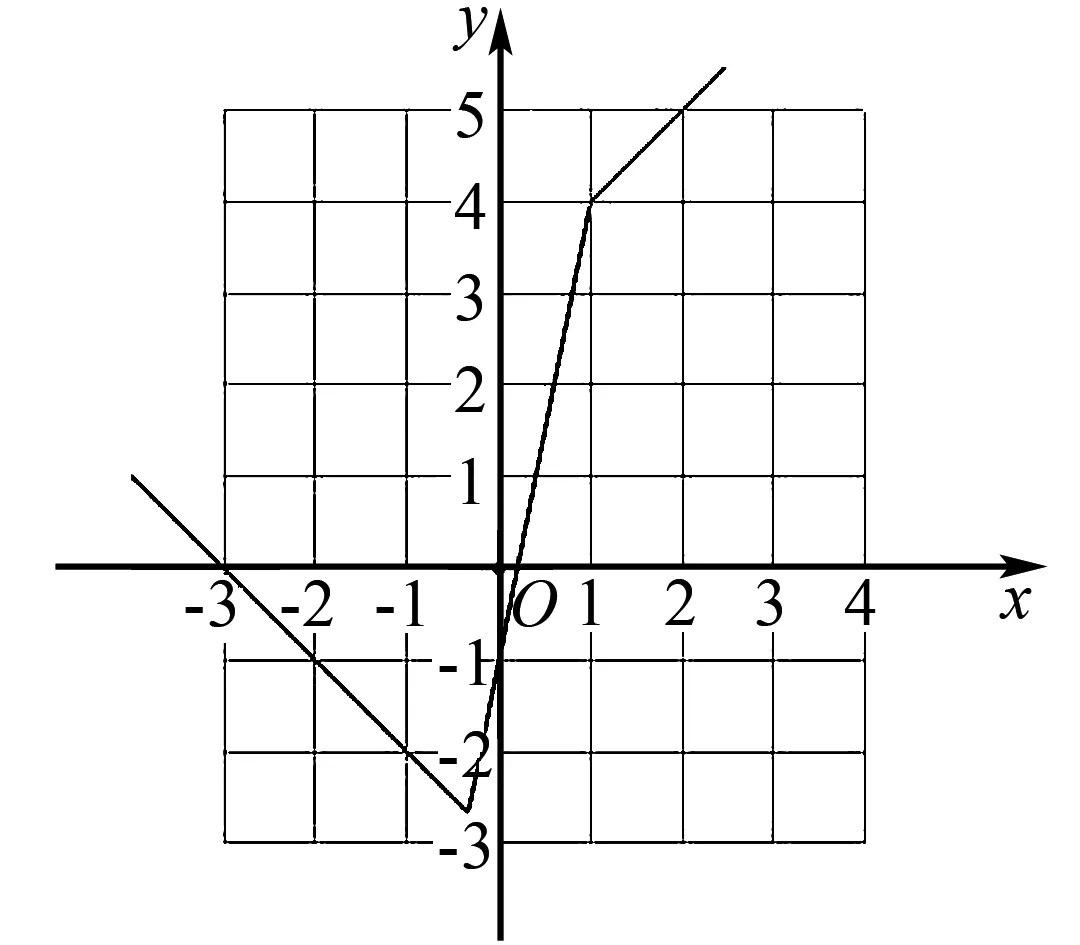
图6

(2)将函数f(x)的图象向左平移1个单位，可得函数f(x+1)的图象，如图7所示：

图7

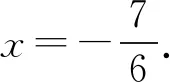
这两年考题都是平移折线图看变量范围，若改为分类讨论求解，就很难计算，用图象能非常直观地求解.在教学中应引导学生多作图，多从图象的上下关系去理解不等关系，学生就能从图象移动中找到不等关系存在时的变量范围.其实这种考题不仅在2021年与2020年出现，我们再看前些年考题，其方法都一样，利用作图可直接方便求解.

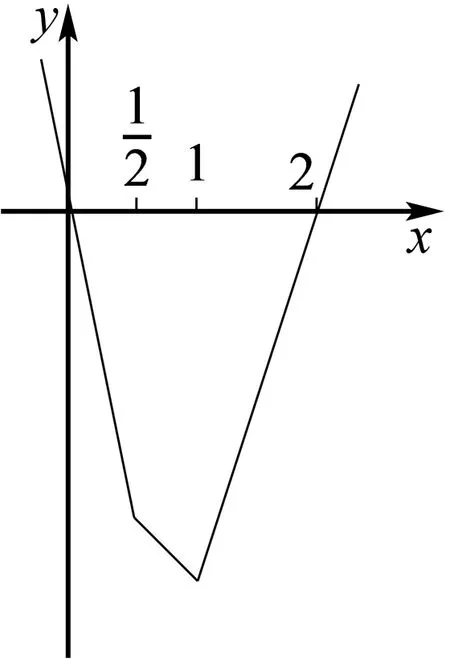
题3 (2018年全国Ⅲ卷文理)设函数f(x)=|2x+1|+|x-1|．

(1)在图8中画出y=f(x)的图象；

图8

(2)当x∈[0,+∞)时，f(x)≤ax+b，求a+b的最小值．

y=f(x)的图象如图9所示．

图9

(2)由(1)知，y=f(x)的图象与y轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3.

故当且仅当a≥3且b≥2时，

f(x)≤ax+b在[0,+∞)成立，

因此a+b的最小值为5．

题4 (2013年全国Ⅰ卷文理)已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.

(1)当a=-2时，求不等式f(x)

解析(1)当a=-2时，不等式f(x)

设函数y=|2x-1|+|2x-2|-x-3,

其图象如图10所示，从图象可知，当且仅当x∈(0,2)时，y<0.

图10

所以原不等式解集是{x|0