2022年高考模拟试题(四)
巨小鹏 赖 杰
(陕西省汉中市龙岗学校 723102)
第Ⅰ卷
一、选择题(本小题共12小题,每小题5分,在每小题给出的4个选项中,只有一项符合题目要求.)

A.i B.-i C.-1 D.1
2.设x,y∈R,则“x≠1或y≠1”是“x+y≠2”的( ).
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件



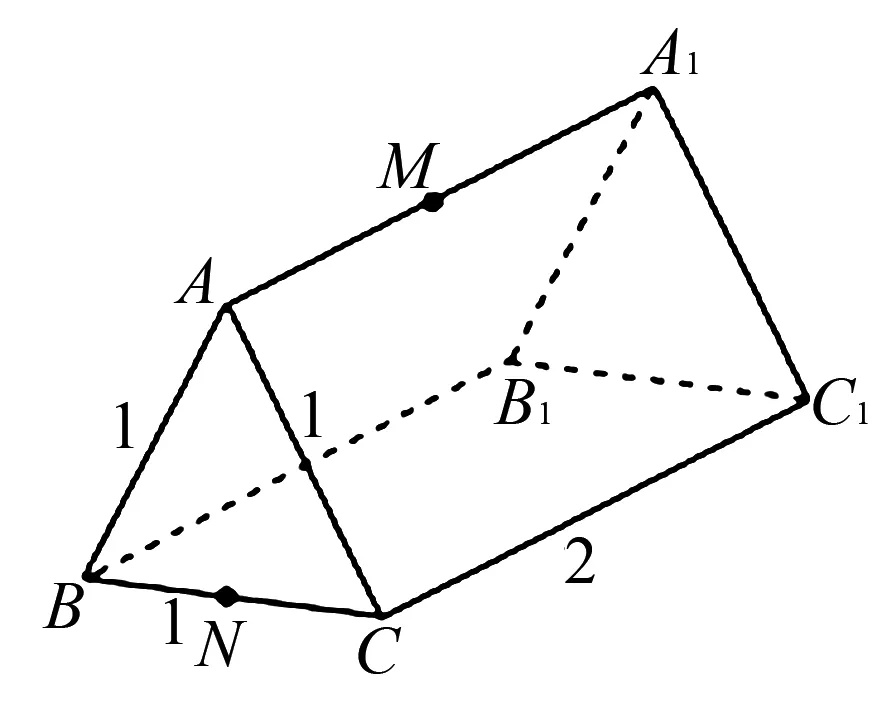
A.b 7.把5名志愿者分配到三个不同的社区,每个社区至少有一个志愿者,其中甲社区恰有1名志愿者的分法有( ). A.14种 B.35种 C.70种 D.100种 A.(-∞,7) B.(-∞,7] C.(-∞,8) D.(-∞,8] 10.某几何体的三视图如图1所示,图中两个点M为直观图中的同一个点M,两个点N也为直观图中的同一个点N,且分别为所在棱的中点,则在此几何体表面上,从点M到点N的路径中,最短路径的长度为( ). 图1 图1 11.卡西尼卵形线是1675年卡西尼在研究土星及其卫星的运行规律时发现的.在数学史上,同一平面内到两个定点(叫做焦点)的距离之积为常数的点的轨迹称为卡西尼卵形线.已知卡西尼卵形线是中心对称图形且有唯一的对称中心.若某卡西尼卵形线C两焦点间的距离为2,且C上的点到两焦点的距离之积为1,则C上的点到其对称中心距离的最大值为( ). 第Ⅱ卷 本卷包含必考题和选考题两部分,第13~21题为必考题,每个试题必须作答。第22~23为选考题,考生根据要求作答. 14.在数列{an}中,若a1=1,a2=3,an+2=an+1-an(n∈N+),则该数列的前2021项之和为____. 15.不等式(x2-2)log0.5x<0的解集是____. (1)求角A; 18.如图2,在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD为长方形,且PD=CD=1,E是PC的中点,作EF⊥PB交PB于点F. 图2 (1)证明:PB⊥平面DEF; (1)求椭圆C的方程; 20.已知各项均为正数的等差数列{an}与等比数列{bn}满足a2=b2=4,又a1,a3,a7+30成等比数列且b5=b1b4. (1)求数列{an},{bn}的通项公式: (2)若cn=anbn-nan-kbn(k∈R),数列{cn}是严格递增数列,求k的取值范围. (1)若a<0时恒有f(x)≥0,求实数a的取值范围; (1)求曲线C1,C2的极坐标方程; 23.已知函数f(x)=|2x+3|-|x-a|(a∈R). (1)当a=1时,解不等式f(x)≥2; (2)若关于x的不等式f(x)≥|x-3|的解集包含[3,5],求a的取值范围. 参考答案 2.B.若x≠1或y≠1,则x+y≠2的逆否命题为:若x+y=2,则x=1且y=1,①当x=4,y=-2时,满足x+y=2,所以充分性不成立,②当x=1且y=1时,x+y=2,所以必要性成立,所以x+y=2是x=1且y=1的必要不充分条件,即x≠1或y≠1是x+y≠2的必要不充分条件, 因为l与OM的斜率的乘积等于2, 所以2a2=c2-a2. 图3 10.B.该三视图对应的几何体是正三棱柱,如图4所示.仅考虑以下三种情况即可: 图4 (3)经侧面、底面到点N,将底面ABC沿AB,BC剪开,并展开至和ACC1A1在同一平面上,则 11.B.设左、右焦点分别为F1,F2,以线段F1F2的中点为坐标原点,F1,F2所在的直线为x轴建立平面直角坐标系,则F1(-1,0),F2(1,0).设曲线上任意一点P(x,y),则 化简得该卡西尼卵形线的方程为 (x2+y2)2=2(x2-y2). 显然其对称中心为(0,0). 由(x2+y2)2=2(x2-y2),得 (x2+y2)2-2(x2+y2)=-4y2≤0, 14.2.由an+2=an+1-an=(an-an-1)-an=-an-1=-(an-2-an-3)=-(an-3-an-4)+an-3=an-4,得{an}是周期为6的周期函数.又a3=a2-a1=3-1=2,a4=2-3=-1,a5=-1-2=-3,a6=-3+1=-2,因为2021=336×6+5,所以S2021=336×(1+3+2-1-3-2)+(1+3+2-1-3)=2. 由不等式(x2-2)·log0.5x<0,得 18.(1)因为PD⊥面ABCD,BC⊂面ABCD,所以PD⊥BC.因为底面ABCD为长方形,所以CD⊥BC.因为PD∩CD=D,所以BC⊥平面PCD.因为DE⊂平面PCD,所以DE⊥BC.因为PD=CD,E为PC的中点,所以DE⊥PC. 因为PC∩BC=C,所以DE⊥平面PBC,所以DE⊥PB.又EF⊥PB,DE∩EF=E,所以PB⊥平面DEF. 图6 20.(1)设数列{an}的公差为d,数列{bn}的公比为q,则由条件有 又q>0,d>0,解得a1=1,d=3,b1=2,q=2. 所以an=3n-2,bn=2n. 又x2+y2=ρ2,y=ρsinθ,所以曲线C2的极坐标方程为ρ=4sinθ. 23.(1)当a=1时,不等式f(x)≥2,即|2x+3|-|x-1|≥2, 解得x≤-6或0≤x≤1或x>1. 所以不等式f(x)≥2的解集为(-∞,-6]∪[0,+∞). (2)关于x的不等式f(x)≥|x-3|的解集包含[3,5],即|2x+3|-|x-3|≥|x-a|在x∈[3,5]时恒成立,即x+6≥|x-a|在x∈[3,5]时恒成立,即-6≤a≤2x+6在x∈[3,5]时恒成立,则-6≤a≤12,所以a的取值范围是[-6,12].

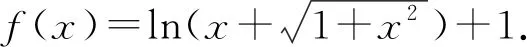



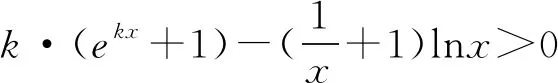


二、填空题(本小题共4小题,其中13~15题每小题5分,16题第一空2分,第二空3分.)
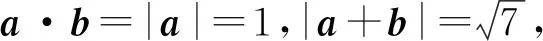

三、解答题(解答题写出文字说明、证明过程或演算步骤,17~21每题12分,选做10分.)

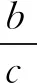







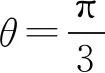

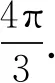
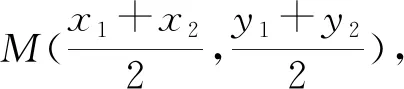
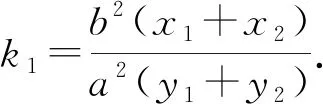



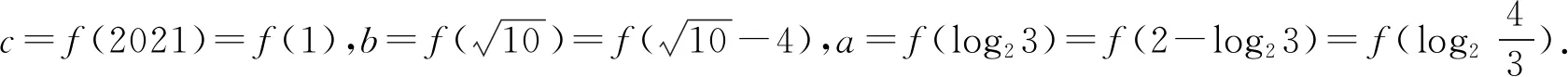




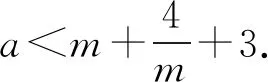

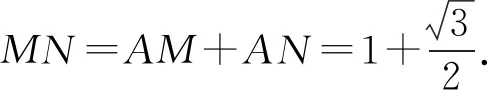
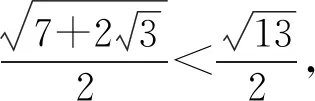

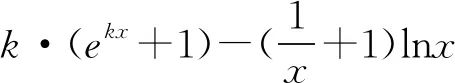
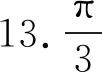





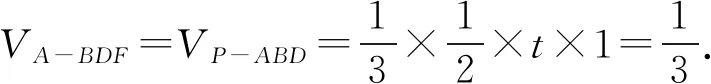






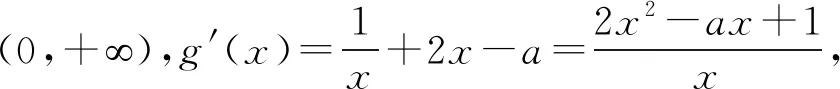
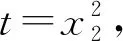

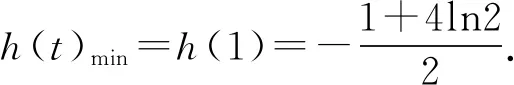


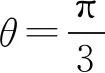

——奇妙的蛋

