矮塔斜拉桥斜拉索不平衡力影响因素分析*

龙平江 杜 镔 唐 志 张剑锋

(1.贵州高速公路集团有限公司 贵阳 550025； 2.贵州省交通规划勘察设计研究院股份有限公司 贵阳 550081)

所谓矮塔斜拉桥，是因为其外形类似斜拉桥，外观上既有塔又有斜拉钢索，但在结构性能上，斜拉索仅分担部分荷载，还有相当部分的荷载由梁的受弯、受剪来承担，“矮塔斜拉桥”即源于斜拉桥的斜拉程度。

有较多学者对矮塔斜拉桥的受力状况进行了分析研究，许磊[1]对矮塔斜拉桥的索梁荷载分担比例进行了分析探讨，并提出曲线矮塔斜拉桥的索梁荷载分担比例公式；文望青等[2]对双幅同步转体矮塔斜拉桥进行了设计研究，验算了结构的各项性能指标，均满足规范要求；鲍英基等[3]通过有限元对PC矮塔斜拉桥的拉索索力、预应力、桥面铺装层厚度及混凝土徐变系数等构件参数进行敏感性分析，得到各项参数变化对主梁位移应力的影响规律；唐双林等[4]采用有限元分析施工阶段大跨非对称矮塔斜拉桥拉索体系的受力性能；蔡小杨等[5]研究柔梁密索体系矮塔斜拉桥的构造特征及受力特点，并对斜拉索布置形式、塔及主梁刚度等敏感参数进行系统分析；彭彬等[6]分析参数变化对车辆荷载作用下主梁内力和变形的影响,得出主梁在活载作用下合理的无索区长度及分布的范围；在矮塔斜拉桥施工与运营阶段，同一根斜拉索在主塔两侧出现不平衡力的情况很多，拉索不平衡力跟桥梁的结构体系、边中跨比及主梁的设计有关[7]，有必要从结构体系、边中跨比及均布荷载布置等方面分析矮塔斜拉桥拉索不平衡力。

1 工程概况

本文以龙井河大桥为研究背景，通过有限元建模计算分析，对矮塔斜拉桥拉索不平衡力的影响因素进行研究。桥型布置图及拉索编号情况见图1。

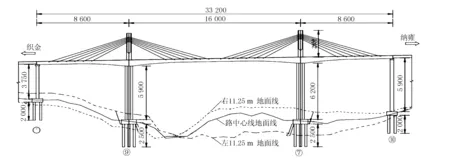
图1 桥型布置图(尺寸单位：cm)

该桥位于厦蓉高速公路贵州境内织金至纳雍段，大桥为跨越山间“V”形河谷而设。龙井河大桥为刚构体系(塔、墩、梁固结)的双塔单索面预应力混凝土曲线矮塔斜拉桥，跨径布置为86 m+160 m+86 m，箱梁中心线处平曲线半径为852.75 m，根据文献[8-9]计算公式，采用刚构体系时本桥索梁活载比(即斜拉索和主梁分别承担的竖向活载百分比)约为0.335。主桥为3跨曲线预应力混凝土矮塔斜拉桥方案，主塔采用独柱型塔柱，采用C50钢筋混凝土；采用双排单索面形式，斜拉索采用低松弛高强度的钢绞线，采用3层防护，每个上塔柱上共12对拉索，全桥共24对拉索；主墩高度分别为59.11 m(8号)和62.11 m(9号)，采用C50钢筋混凝土。7号与10号过渡墩采用薄壁空心墩，群桩基础，桩基为钻孔桩。引桥桥墩采用双柱式圆形实心墩，桩基础，桥台采用扩大基础。桥梁全宽28 m。

2 有限元模型建立

本文采用桥梁结构专用分析软件对本桥进行有限元仿真分析；结构计算采用空间梁单元模型，以主梁轴线为基准划分结构离散图，主塔、主梁和主墩为空间梁单元，斜拉桥拉索为平面桁架单元，边墩按刚性计算；主梁悬臂浇注区段按每个施工节段并兼顾主梁斜拉索锚固位置划分单元，全桥模型共有271个节点，划分234个单元，其中主梁划分为122个单元，主塔与主墩各划分为20，44个单元，斜拉索划分为48个单元。模型构件材料参数见表1。

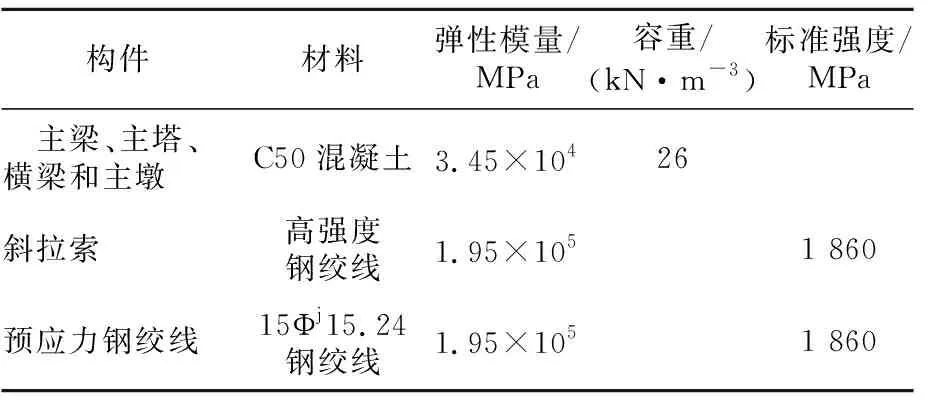
表1 材料参数表

由于结构主梁的有限元模拟采用的是“单梁”模式，所以未对主梁顶板横向预应力及腹板竖向预应力进行模拟。有限元分析模型见图2。

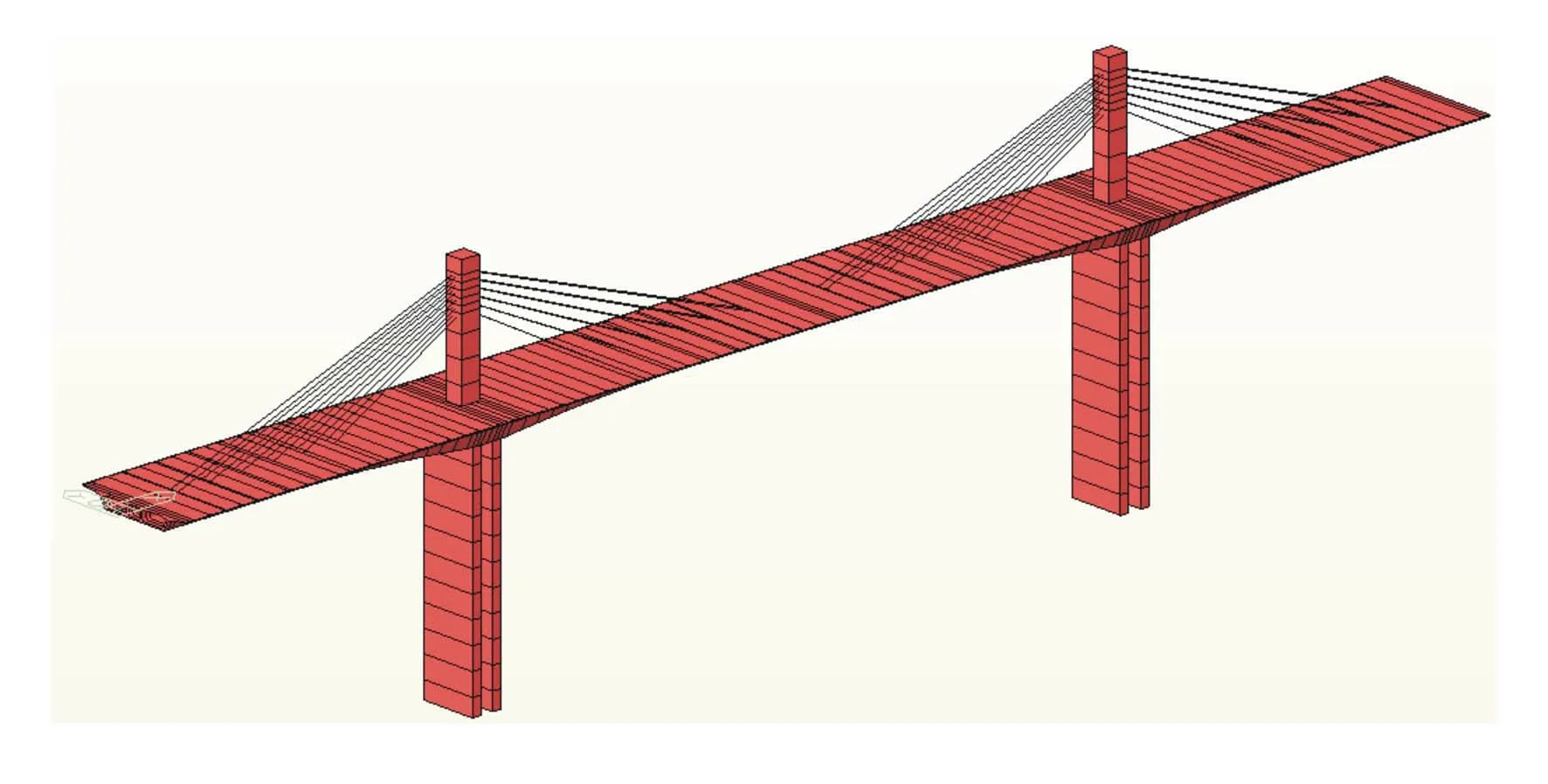
图2 矮塔斜拉桥有限元模型

3 结构体系对拉索不平衡力的影响

由于该桥为对称结构，取织金段方向一半桥梁为研究对象。选取3种结构体系(刚构体系、半漂浮体系和塔梁固结体系)作为分析工况，施加荷载为桥梁自重+均布荷载+预应力作用，计算桥梁边中跨对称拉索织金塔1号～6号的索力值及拉索不平衡力，结果见表2。

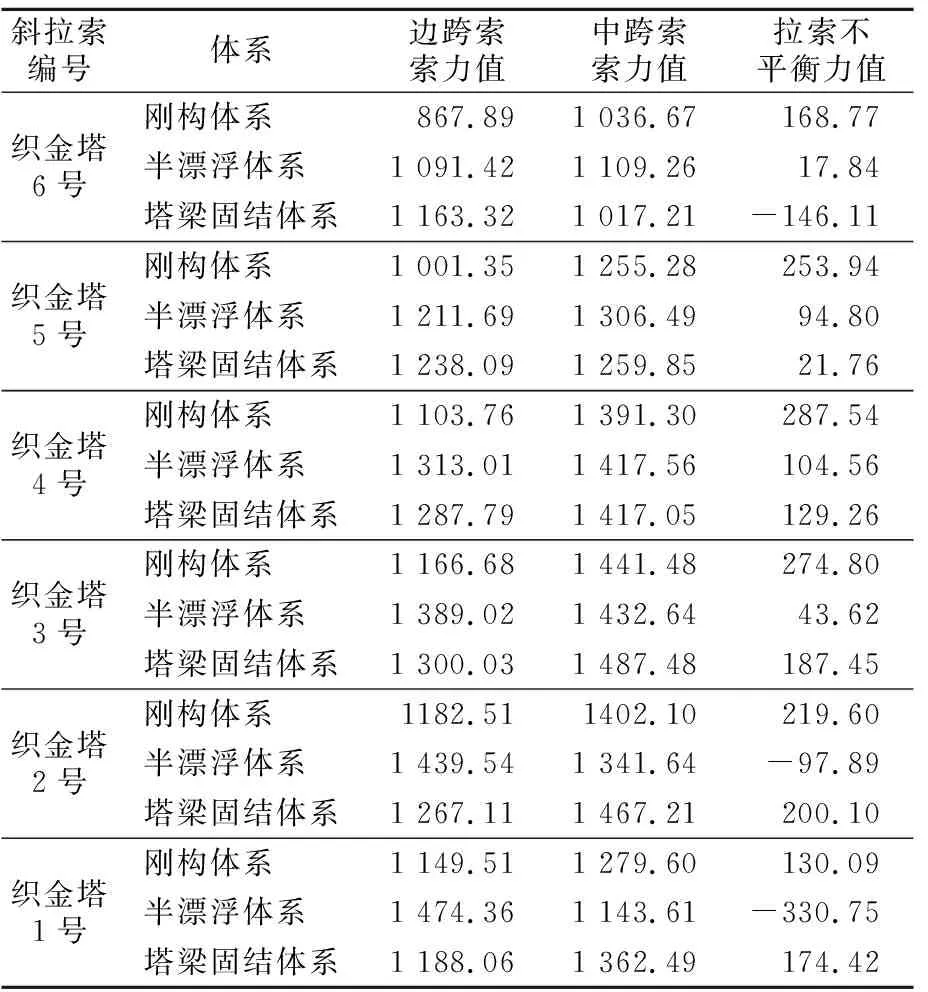
表2 矮塔斜拉桥不同体系下拉索织金塔1号～6号索力及拉索不平衡力 kN

由表2可见，无论哪种结构体系，同一根拉索在索塔两端的拉索内力均不相等。

通过分析比较，在仅改变结构体系，保持全桥荷载和边中跨比不变的前提下，3种体系对应的拉索不平衡力程度稍有差别，3种结构体系下织金塔各拉索不平衡力的变化规律见图3。

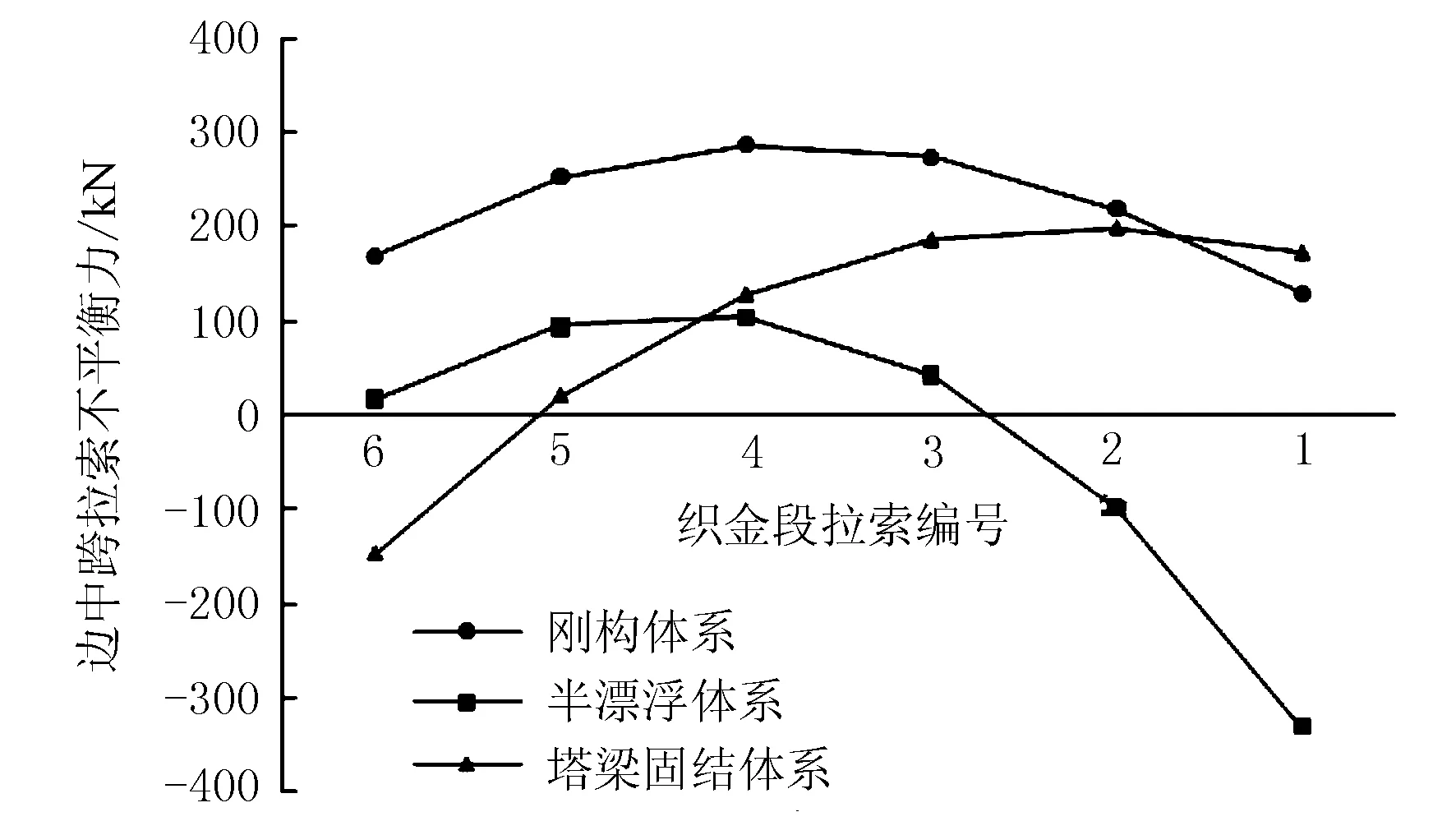
图3 3种结构体系下织金塔各拉索不平衡力的变化规律

由表2和图3可见：①刚构体系下，织金塔1号～6号拉索的拉索不平衡力普遍超过100 kN，最大为织金塔4号拉索，接近300 kN；②半漂浮体系下，靠近塔根的织金1号拉索的拉索不平衡力最大，绝对值超过300 kN，织金塔6号拉索的拉索不平衡力最小，不超过20 kN，织金塔2号、4号和5号拉索不平衡力绝对值接近，均在100 kN附近；③塔梁固结体系下，织金塔5号拉索不平衡力最小，仅21.76 kN，织金塔2号、3号拉索不平衡力接近于200 kN，织金塔4号和6号拉索不平衡力则接近150 kN。由此可见，刚构体系下各拉索不平衡力较大，各拉索不平衡力变化较均匀。半漂浮体系和塔梁固结体系下部分拉索不平衡力表现出较大的差异性，半漂浮体系下对跨中附近拉索最大，塔梁固结体系下5号拉索不平衡力最小。

4 边中跨比对拉索不平衡力的影响分析

选取对各拉索不平衡力最为显著的结构体系之一——刚构体系为研究对象，拟定了边中跨比分别为0.5、0.525、0.55、0.575和0.6共5种工况，人为给定全桥均布荷载100 kN/m，计算拉索的索力，限于篇幅，仅给出织金塔1号～6号拉索的不平衡力，结果见表3，5种边中跨比条件下织金塔1号～6号拉索不平衡力变化规律图见图4。

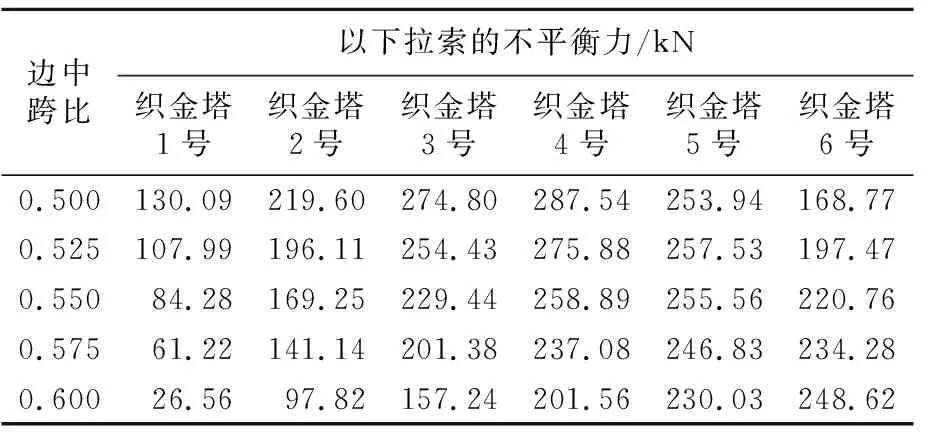
表3 矮塔斜拉桥不同边中跨比下拉索

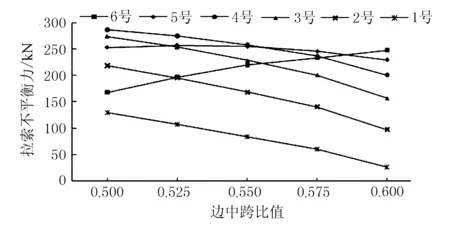
图4 5种边中跨比条件下织金塔1号～6号拉索不平衡力变化

由表3和图4可见，织金塔1号～4号拉索的不平衡力基本随着边中跨比增大呈近似线性递减趋势， 5号拉索的不平衡力随边中跨比增大变化不明显，而6号拉索的不平衡力则随边中跨比的增大呈现近似线性递增的趋势。究其原因主要是由于中跨一端无墩塔约束，而边跨两端均有墩塔约束，使得边中跨主梁刚度出现较大差别，从而导致塔根附近织金塔1号～4号拉索不平衡力最大，中跨织金塔6号拉索不平衡力最小，织金塔5号拉索因为正好介于两类拉索之间，出现随边中跨比增加变化不明显的情况。

5 荷载布置对拉索不平衡力的影响分析

以本文研究对象为例，由于矮塔斜拉桥边跨拉索两端有墩约束，而中跨拉索仅一端有墩约束，体系存在一定差异，因此，本节考虑2种荷载变化情况进行分析。

5.1 中跨荷载不变，改变边跨荷载

以刚构体系矮塔斜拉桥为研究对象，给矮塔斜拉桥边、中跨提供初始均布荷载100 kN/m，不断增加边跨均布荷载，计算出拉索的索力。限于篇幅，本文仅给出织金塔1号～6号拉索的不平衡力结果见表4，拉索不平衡力随边跨荷载的变化规律见图5。

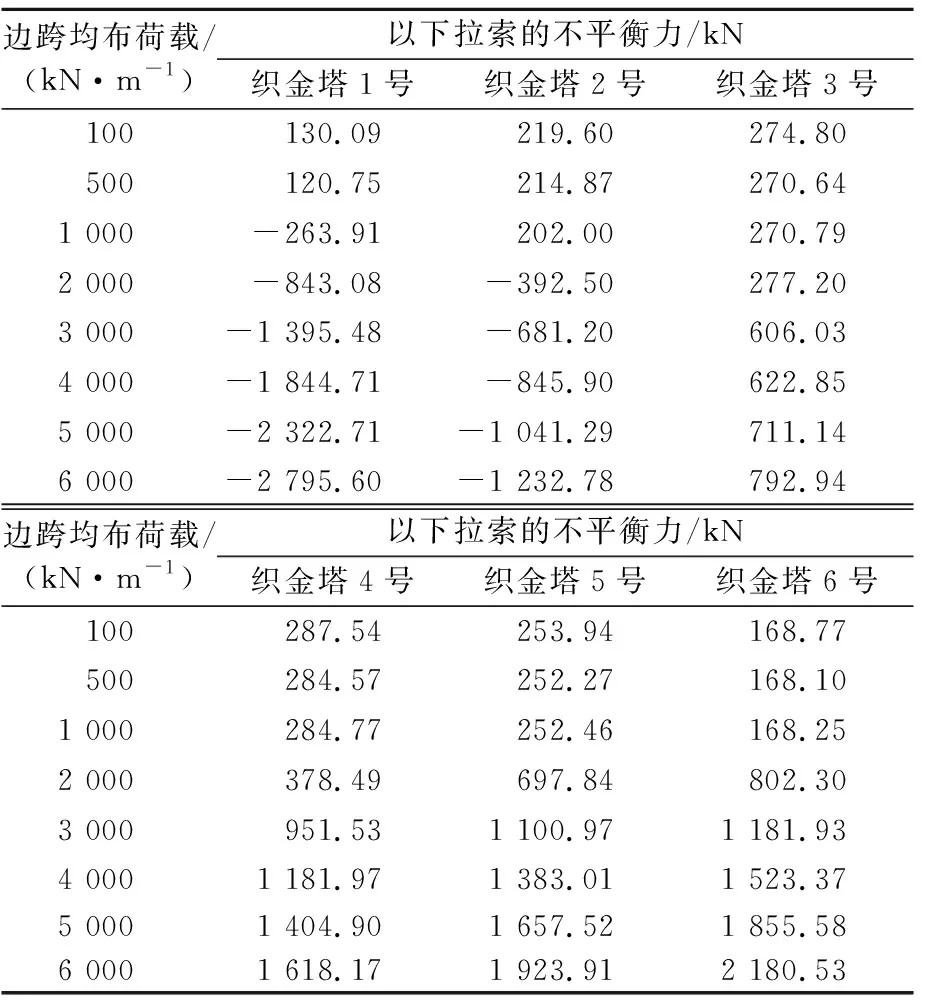
表4 矮塔斜拉桥边跨不同均布荷载下

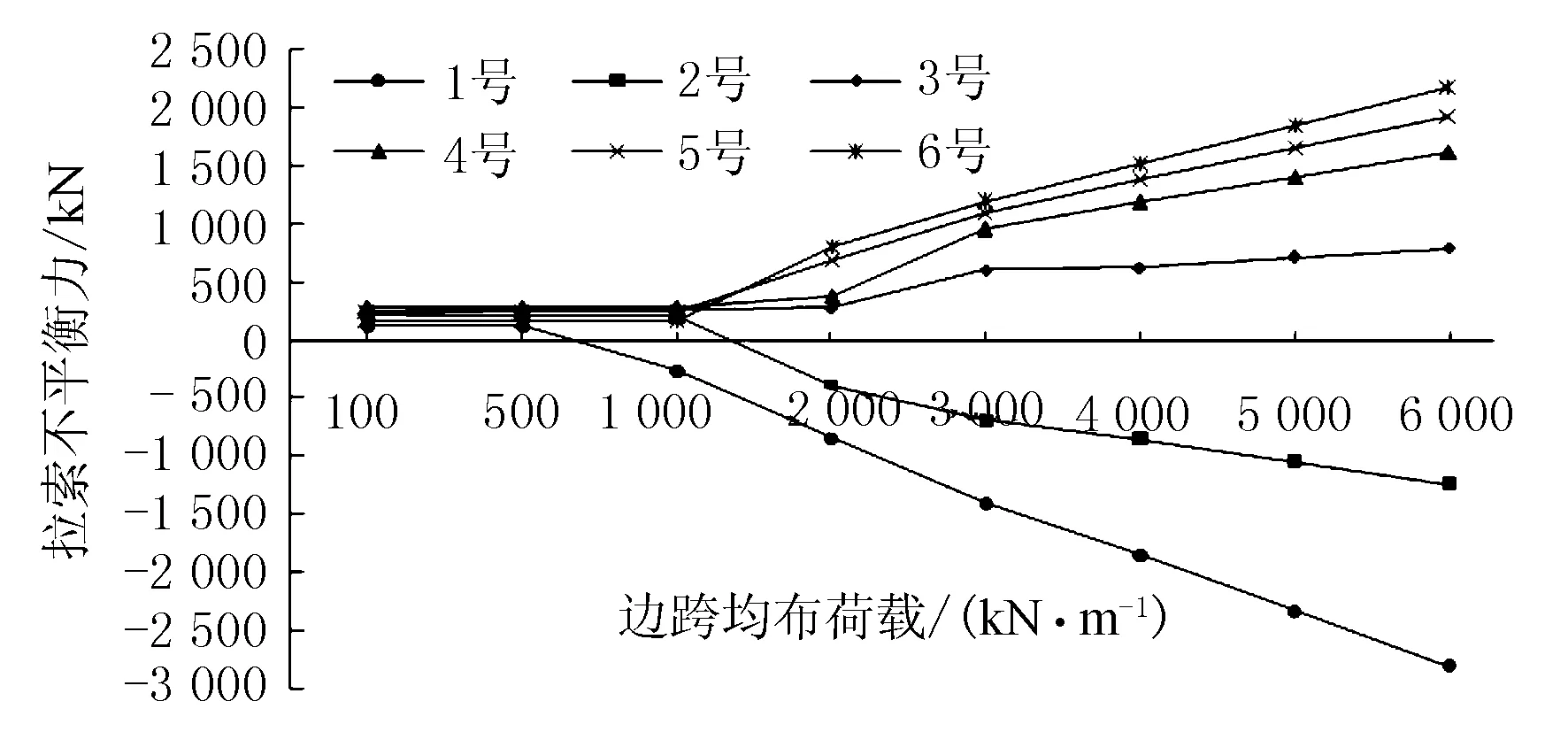
图5 织金塔1号～6号拉索不平衡力随边跨荷载的变化规律

由表4和图5可见：①织金塔1号、2号拉索不平衡力在边跨荷载从100 kN/m增加到500 kN/m (2号拉索1 000 kN/m)时变化不明显，但从500 kN/m (2号拉索1 000 kN/m)增加到6 000 kN/m时呈现明显递减趋势。②在保持中跨荷载不变仅改变边跨荷载时，织金塔3号～6号拉索不平衡力在边跨均布荷载从100 kN/m增加到1 000 kN/m时变化不大，但从1 000 kN/m增加到6 000 kN/m时，明显呈现线性递增规律。

5.2 边跨荷载不变，改变中跨荷载

同样以刚构体系矮塔斜拉桥为研究对象，对矮塔斜拉桥边、中跨提供初始均布荷载100 kN/m，不断增加中跨均布荷载，计算拉索的索力。限于篇幅，本文仅给出织金塔1号～6号拉索不平衡力计算结果见表5，拉索不平衡力随中跨荷载的变化规律见图6。

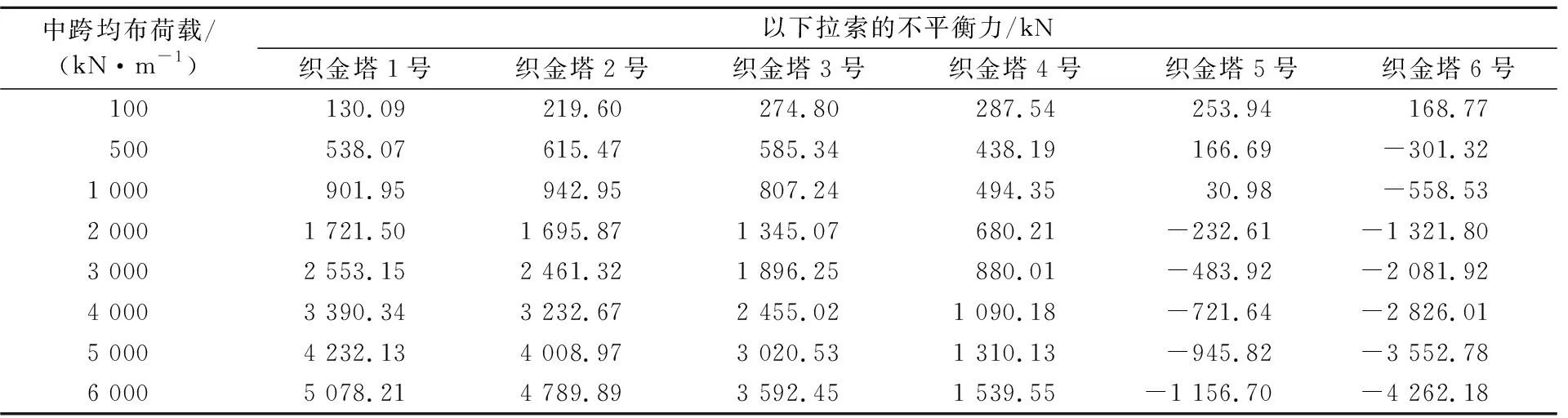
表5 矮塔斜拉桥边跨不同均布荷载下织金塔侧1号～6号拉索不平衡力

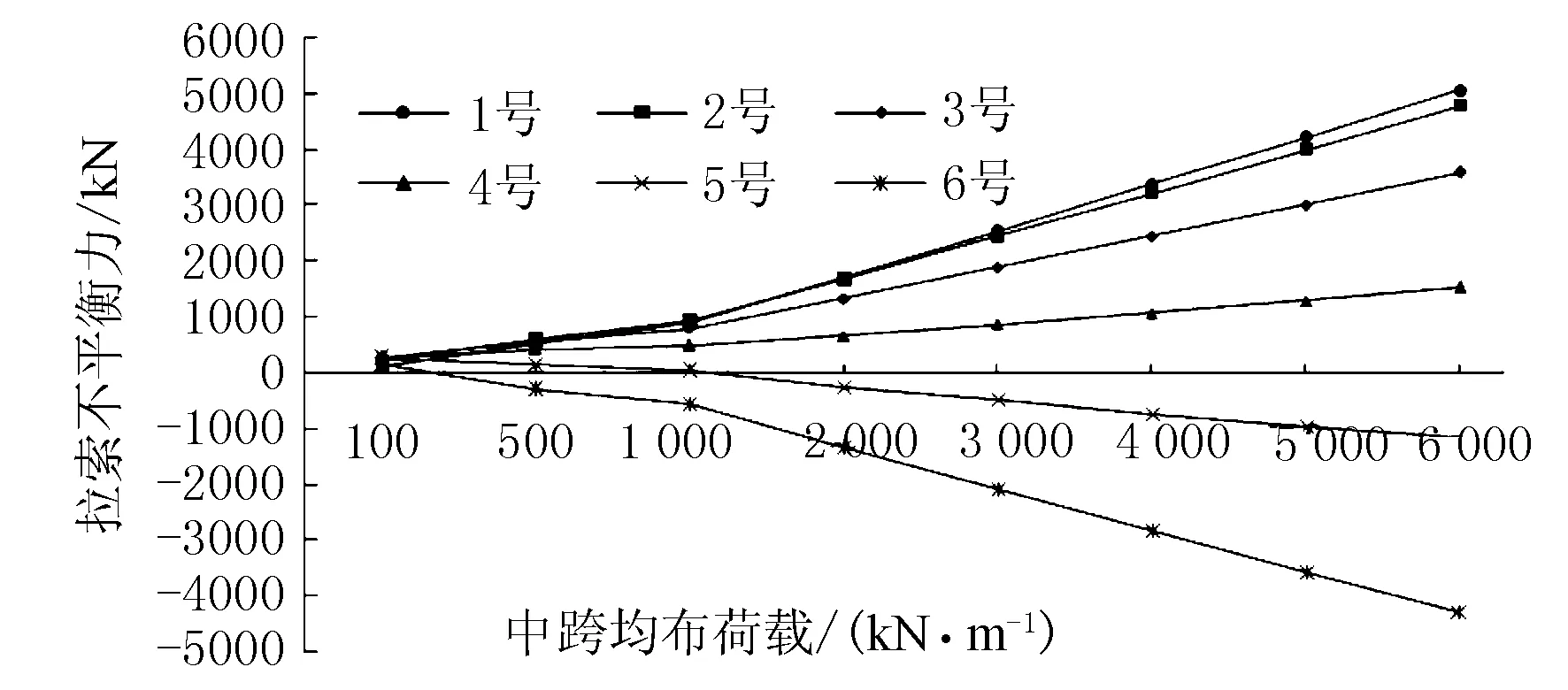
图6 织金塔1号～6号拉索不平衡力随中跨荷载的变化规律

由表5和图6可见，当保持边跨荷载不变，逐步增加中跨均布荷载时，织金塔1号～6号拉索不平衡变化趋势相比于仅改变边跨荷载要稳定得多，织金塔1号～4号拉索不平衡力随中跨荷载增加呈现线性递增的趋势，织金塔5号和6号拉索不平衡力呈现先线性递减后反向递增的趋势。

6 结论

针对矮塔斜拉桥拉索不平衡力现象，本文采用数值模拟手段并结合矮塔斜拉桥相关的研究成果，对矮塔斜拉桥拉索的不平衡力的影响进行了计算和分析，得到以下结论。

1) 刚构体系下各拉索不平衡力较大，各拉索不平衡力变化较均匀，半漂浮体系和塔梁固结体系下部分拉索不平衡力表现出较大的差异性。

2) 边中跨比对拉索不平衡力有一定的影响，1号～4号拉索的不平衡力变化随边中跨比呈线性递减，5号拉索影响不明显，6号拉索的不平衡力变化随边中跨比呈线性递增。

3) 荷载布置对拉索不平衡力有很大的影响，荷载布置对靠近跨中和塔根处的拉索(1号、6号拉索)拉索影响最大，对于中间拉索的影响相对较小，且中跨荷载布置的影响明显大于边跨荷载的布置。