基于机器学习的路表温度预估方法研究*

杨书杰 彭 嫣

(同济大学道路与交通工程教育部重点实验室 上海 201804)

路面结构处于复杂的环境变化中，在与外界环境进行热交换的过程中，路面温度也随之发生变化。路面材料的使用性能直接受到温度影响。例如，路表温度过高易使车辆轮胎内气压升高进而有爆胎的危险、路表温度过低则易结冰降低路面安全性能。因此，对中短期时间尺度内的路表温度进行预测具有重要的社会经济价值。现有的路面温度预估方法主要有理论法与统计法两类。

严作人[1]依据热传导理论建立了层状体的温度场问题求解方法。理论法基于传热学原理，建立并求解了路面温度场偏微分方程，得到了未来某时刻的路面温度。该方法物理意义明确、普适性强，然而需要的参数较多，在实际运用中，方程中的热工参数也难以准确获取，这些因素限制了模型的应用。

传统的统计法在对路面温度进行长期监测后采集到大量的相关数据，基于数理统计的原理，建立了路面温度与各种气象因素之间的多元回归模型，该方法所需参数较少且较易获得。李伊[2]、张曦[3]等采用多元回归模型建立了路面温度与气象参数之间的回归方程，但由于不同研究人员在方程的形式、参数等关键问题处理上均有一定的差异，限制了模型的推广使用。

近年来，机器学习理论广泛运用于各学科中，由于其具有数据处理效率高、解决非线性问题能力强的特点，在预估路面温度的课题当中得到了一定的应用,取得了良好的效果[4-6]。

1 数据来源

依托于山西大同国家气象观测站，在站点内铺设了水泥、沥青2种路面结构试验区，利用温度传感器采集路表温度，传感器于路面结构层施工时埋设，埋设位置位于结构表面中心处，采集频率为10 min/次，精度为±0.5 ℃，无限传输设备可以定时上传数据至计算机中。同时，气象站点每隔1 h采集1次气温、相对湿度、太阳辐射、风速等气象数据，时间自2009年7月-2010年7月。数据上传后，气象数据由气象站工作人员进行校验，路面温度数据则依据传感器测温范围进行了异常值处理。铺面结构示意见图1。

图1 铺面结构示意图

2 模型输入特征

模型特征应基于路面结构的实际热交换过程。故当路面各结构层之间接触良好且无热阻情况下，路面温度场θi(z，t)的偏微分方程可表示为

(1)

在路表处有

(2)

式中：θi(z,t)为第i层距路表深度z处t时刻的温度；αi为第i层导热系数；q1(0,t)为t时刻的路表热流；λ1为路表结构层的导热系数。

对于接近表面的结构层而言，其热交换主要由以下两部分构成。

1) 与下层结构的热交换。路表与表面以下的结构层存在温度梯度,这导致两者之间发生一定的热交换。由于底部温度在24 h内振幅一般小于0.5 ℃，故结构层内的热源主要是路表，谈至明[7]指出，可以根据历史时刻的路表温度对结构层的温度进行估计。故有必要将历史时刻的路表温度作为特征。本文选取过去4 h的路表温度纳入模型中。

2) 与外界环境的热交换。外界气象要素的变化是路表温度变化的根本原因，太阳辐射与天空逆辐射是路表的热源，同时在风的作用下，路表与空气通过热对流进行热量交换。因此，应将太阳辐射、气温、风速等气象参数纳入模型当中，模型输入的参数见表1。

表1 模型输入参数

3 模型与方法

3.1 模型介绍

LightGBM是微软公司提出的一种实现梯度提升决策树(GBDT)的集成学习框架，其核心是GBDT算法，基于boosting的集成思想，通过若干个CART决策树作为基学习器进行模型的迭代，并最终生成了一个强学习器，实现了对目标变量的预测。相较于传统GBDT框架，其在不降低精度的条件下能大幅加快训练速度，广泛应用于各种预测问题中。

模型的输入为训练样本D={(x1,y1),(x2,y2),…,(xm,ym)},损失函数L(y,c)，基学习器的个数N。输出为路面温度预估值yi。GBDT算法的训练流程如下。

步骤1。初始化模型，得到初始学习器

(3)

步骤2。迭代n=1，2，…，N个基学习器：

1) 遍历i=1,2,…,m个训练样本，对第i个样本，计算当前模型在损失函数中的负梯度。

(4)

2) 拟合上一步得到的残差，得到1棵新回归树。新回归树的叶子节点区域为Rnk，k=1,2,…,J。J为回归树的叶子节点个数。

3) 遍历k=1,2,…,J个叶子节点，计算最优拟合结果。

(5)

4) 更新学习器

(6)

损失函数采用实际意义明确的均方差函数

(7)

式中：xi为输入变量；yi为输出变量；f(xi)为预测值；n为样本数。

3.2 预估方法

现场实验共对水泥、沥青2种路面进行了为期1年、10 min/次的数据采集，各得到了5×104余条路面温度数据。气象数据每个整点记录1次，其中，太阳辐射为小时内辐射总量，其余参数为小时内平均值。为了确保路面温度数据与气象数据相匹配，取整点时刻的路表温度作为训练数据，与气象数据共同送入模型中训练。利用python平台的LightGBM、scikit-learn等相关库开展实验，训练集与测试集的划分比例为4∶1,利用网格搜索得到最佳的超参数后，分别得到了1 h与3 h的预估结果。

预估结果的评价指标采用均方根误差RMSE与预报准确率Accuracy 2个指标进行评价，以允许误差为3 ℃计算准确率[8]，两指标的计算公式分别见式(8)和式(9)。

(8)

(9)

式中：yi_true为实测温度，℃；yi_pred为预估温度，℃；n为样本数。

4 结果分析

4.1 1 h预估精度

预估未来1 h的路面温度时，测试样本上沥青路面的RMSE为1.12 ℃,水泥路面为0.82 ℃，2种路面的预估温度与实测温度对比图均围绕45°等值线上下波动。1 h预估温度与实测温度比对结果见图2。

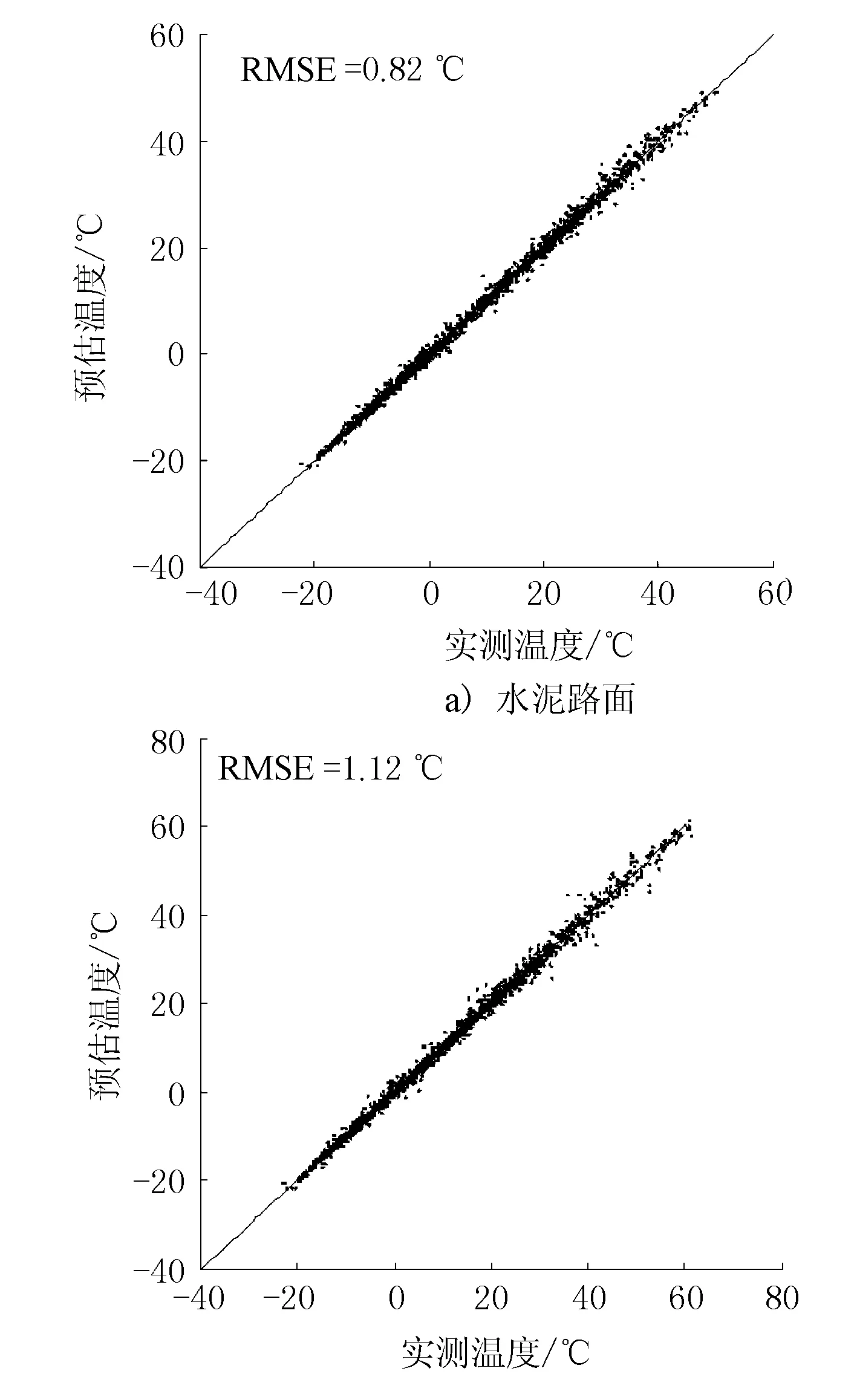
图2 2种路面1 h预估结果

4.2 3 h预估精度

预估未来3 h内的路面温度时，气象要素的时间尺度从1 h增加为3 h，将未来3 h内的太阳辐射、风速、气温输入模型当中，测试样本上水泥路面的RMSE为1.31 ℃，沥青路面为1.86 ℃，2种路面的预估精度均出现了一定程度的下降。3 h预估温度与实测温度比对结果见图3。

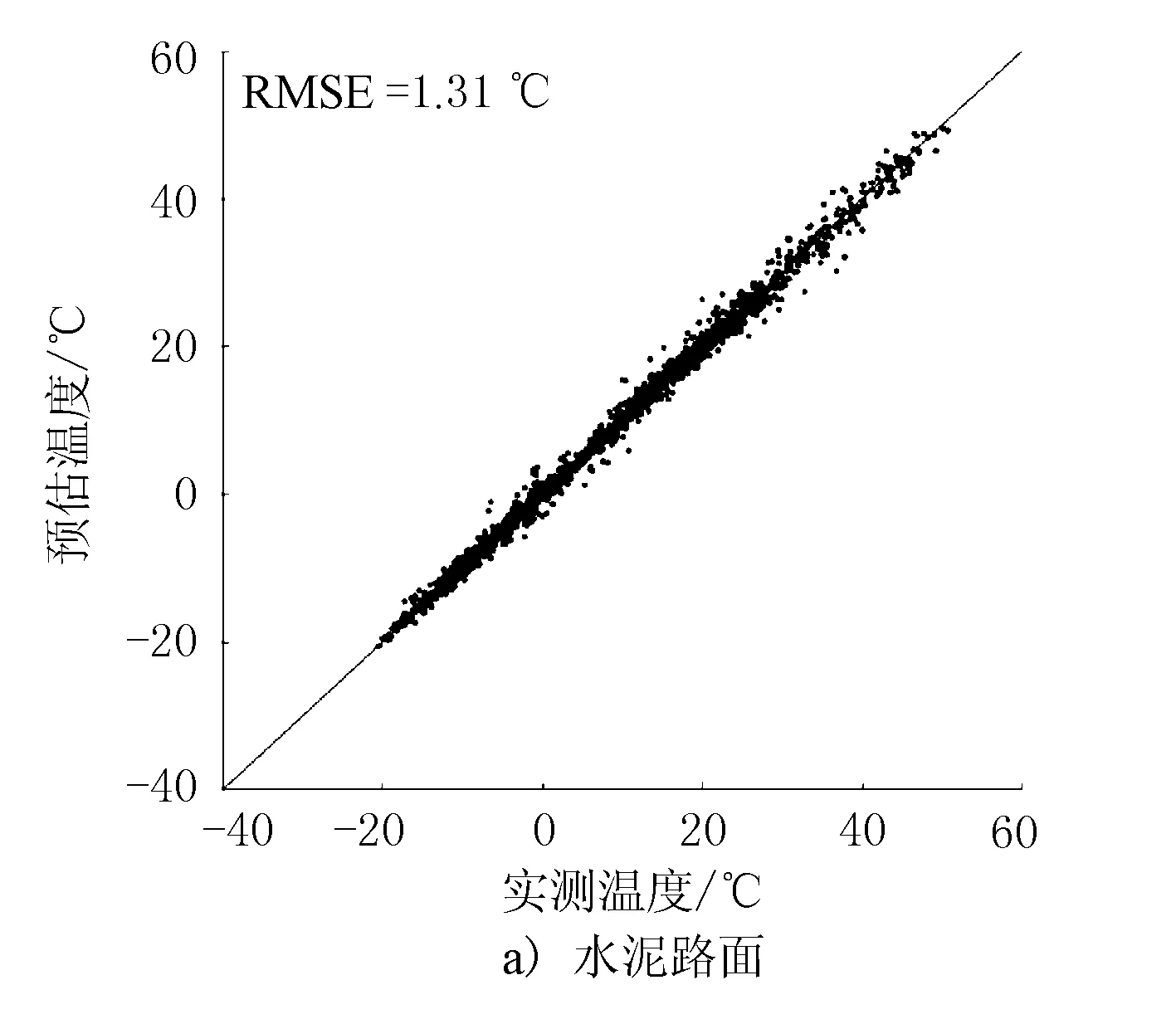
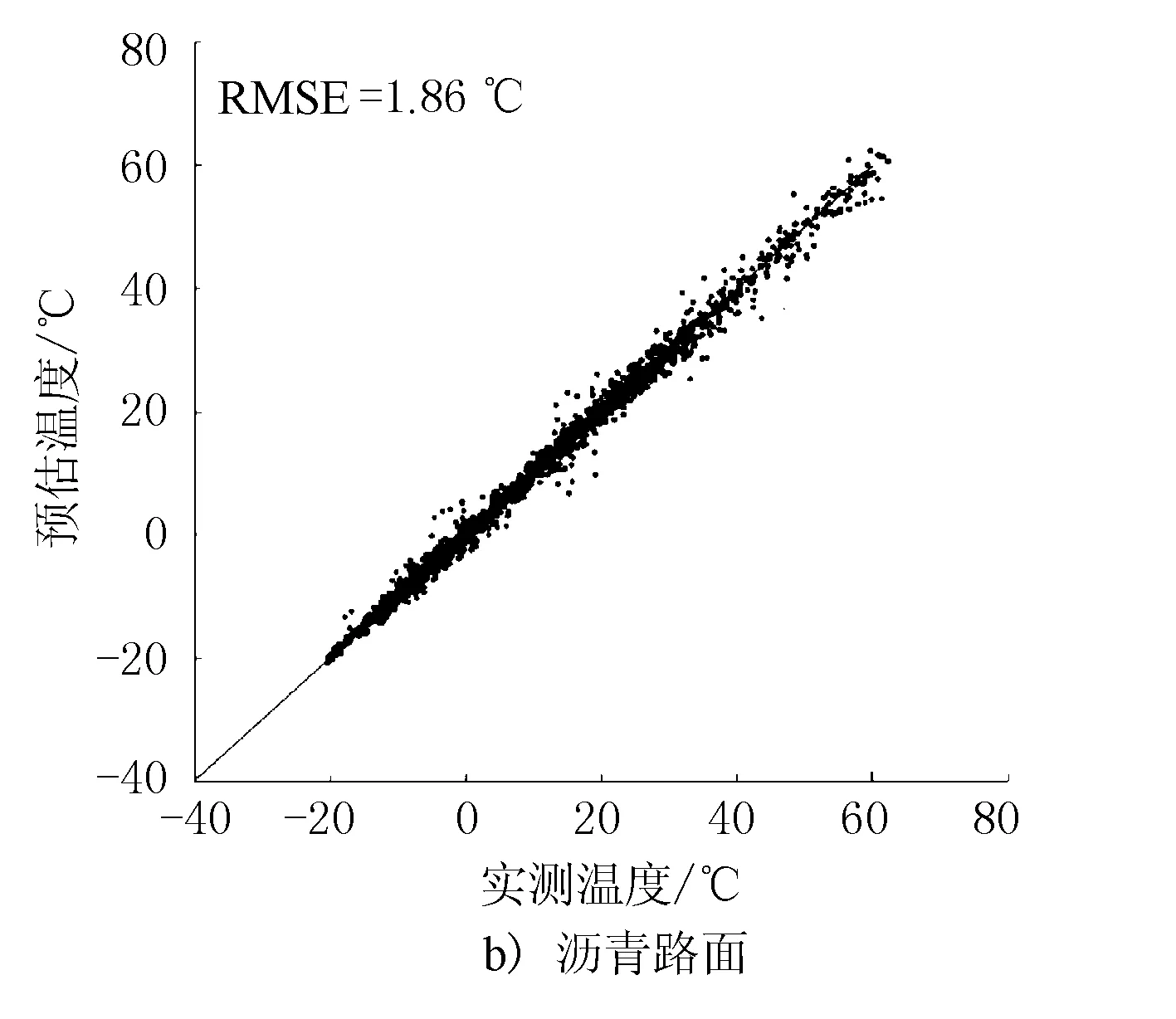
图3 2种路面3 h预估结果

比较图2与图3发现，在低温阶段3 h与1 h的预测效果均较好，实测温度与预测温度均匀分布在45°等值线上下，当路面温度大于40 ℃时，3 h时间尺度的预估结果精度出现了明显下降，这表明误差的增大主要是由于高温阶段预估结果的精度下降造成的。其主要原因可能是夏季正午前后路表温度快速上升，由于云对太阳辐射有削弱作用且其分布具有随机性，导致路面温度变化的不确定性增加，进而导致预估精度下降。

由图2、图3还可知，2种时间尺度下水泥路面的RMSE均小于沥青路面，准确率也高于沥青路面，水泥路面的预估效果优于沥青路面的原因可能在于沥青的体积热容较小而辐射吸收能力较强，导致沥青路面温度变化对外界环境的噪音更为敏感。

预估结果的精度与准确度比较结果见表2，除沥青路面3 h的预估结果外，2种时间尺度下路表温度的预估精度都达到了95%以上。

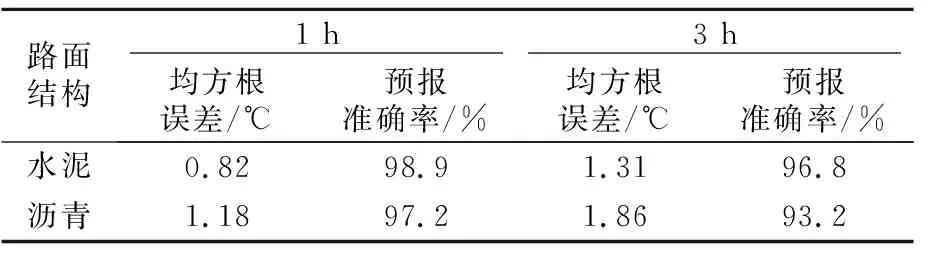
表2 预估结果精度比较

在相同地区同一数据集上的研究中，使用理论法进行预估时RMSE在2.5 ℃上下[9-10]，其他学者使用多元回归等方法进行预估时RMSE在2～3 ℃之间。机器学习的方法对路表温度进行预估具有较好的效果，在未来进一步的研究中，随着数据量的增加与气象参数的拓展，其预估效果仍有一定的优化空间。

5 结语

本文采用了LightGBM这一机器学习集成框架在中短期时间尺度内对路面温度进行了预估，得到了如下结论：

1) 相较于理论法与传统的经验法，该方法具有需要参数少、中间参数处理简单的特点，特别是在数据量较大时，机器学习的方法能够更充分有效地利用数据。

2) 在沥青、水泥2种路面结构上，1 h与3 h 2个时间尺度的预估结果均取得了良好的效果，RMSE在0.82～1.86 ℃之间，准确度在93.2%～98.9%之间，水泥路面的预估效果优于沥青路面。

3) 低温状况下2种路面在中短期时间尺度下预估精度均较好，预估温度与实测温度均匀分布在45 ℃等值线上下；高温状况下预估精度有所下降。

4) 影响预估结果的主要因素有估计时效、结构类型与气象因素。其中，由于气象因素较为复杂，难以全面考虑，且不可避免地存在着各种噪音，造成了预估结果存在一定误差。预估时效的延长，造成了预估误差的叠加；相对与水泥路面，沥青路面的温度变化对环境因素更加敏感，当气象因素存在一定的不确定性时，其预估结果的误差将大于水泥路面。

由于不同地区具有不同的气候特点，加之路面结构的热工参数也有差异，模型能否进一步推广于其他地区尚需在新的数据集上加以验证。如何进一步合理纳入云等气象要素作为特征以降低高温状况下路表温度的预估误差，仍有待进一步研究。