基于SD的装配式建筑施工安全监管演化博弈研究*
张跃斌,易 欣,宋璋玉,陈景川
(中南林业科技大学 土木工程学院,湖南 长沙 410004)
0 引言
建筑工业化是实现建筑产品节能、可持续发展的新型建筑生产方式,装配式建筑则是落实建筑工业化的重要路径[1],但由于大规模采用预制构件,施工现场往往运用更多的大型机械设备进行并行交叉作业[2],再加上现阶段技术熟练的施工人员数量不足,难以满足实际需要,容易引发施工安全事故[3]。此外,装配式建筑高度工业化的模块营造方式对施工现场安全管理提出了全新要求,由于目前的安全管理体制尚不成熟,未能对影响施工安全的风险因素进行全过程的有效防控[4],所以导致施工过程存在较大的安全隐患。
目前,已有学者对装配式建筑施工安全进行了相关研究。在影响因素和危险源辨识方面,李皓燃等[5]从装配式建筑全寿命周期的角度探讨了安全因素之间的作用机理,段永辉等[6]进一步运用SEM比较了装配式建筑施工安全各种因素的影响程度。根据这些因素指标体系,李文龙等[7]提出了熵权-未确知测度理论的装配式建筑施工过程安全评价模型。为改善评价过程不确定信息的处理问题,信息化技术逐渐应用到装配式建筑施工安全监管中,为装配式建筑施工安全管控提供1种新思路[8]。现有成果多集中于施工安全的客体分析,仅验证了这些因素能够影响装配式建筑施工安全,但却难以解释在安全技术措施不断完善、管理水平日益提高的情况下,为何仍旧存在故意违规作业,即对不安全行为产生的主体原因仍缺乏说服力。实际上,安全事件是由于系统中主体行为在效率梯度和效益梯度共同作用下对正常状态的偏离,安全事故管控要重点关注系统中的行为主体及行为策略背后的决策逻辑[9]。现实中,由于目前装配式建筑比传统方式更高的成本,施工单位在利益驱使下可能在事故风险与经济利益间进行博弈,而政府监管部门为了自身利益,也可能与其合谋[10]。考虑到有限理性下双方往往需要通过获取对方更多信息来不断调整自己策略,故演化博弈理论是解决此类问题的有效工具,其已被广泛应用于航空安全监管[11-12]、食品安全监管等方面[13]。
由于装配式建筑施工方法和设备仍在不断发展中,施工单位的施工成本、安全投入和政府监管部门的监管成本等相应地也在不断变化中,因此相较于传统的单次博弈静态监管方式,采取动态监管机制更符合实际,即政府监管部门可以根据施工单位忽视安全管理的主观意愿(概率)来动态调整惩罚力度。同时,考虑到这种惩罚力度也不可能只是单调递增而应在达成监管目标后适当放缓,否则如超过了施工单位承受能力可能导致“破罐子破摔”而适得其反。因此,政府监管部门的动态惩罚力度与施工单位忽视安全管理的主体行为是1种非线性关系。鉴于此,本文在分析政府监管部门与装配式建筑施工单位安全监管关系的基础上,引入非线性动态惩罚函数构建装配式建筑施工安全的动态监管机制,并运用 SD仿真分析各演化均衡解的稳定状态及收敛情况,可针对性地提高政府监管部门的安全监管效率和效果,从而推动施工单位主动加强安全管理,为完善我国装配式建筑施工安全监管体系提供理论参考。
1 模型假设与构建
政府监管部门、施工单位都是有限理性的演化博弈主体,并在反复博弈过程中不断优化自身策略选择。政府监管部门的策略空间——强监管与弱监管,令ωg=(强监管,弱监管);施工单位对应2个策略选择——加强安全管理与忽视安全管理,即ωc=(加强安全管理,忽视安全管理),模型涉及的参数意义说明如表1所示。

表1 模型参数说明Table 1 Explanation of model parameters
假设1:政府监管部门以α(0≤α≤1)概率对施工单位施工安全状况进行监管,α表示政府监管部门的监管力度,α=1表示监管部门对施工单位进行强监管,α=0表示监管部门弱监管。施工单位以β(0≤β≤1)概率选择加强安全管理,β表示施工单位对施工安全管理的努力程度。β=0表示施工单位对施工安全不够重视,安全保障成本投入不足,此时发生安全事故的概率为σ(0≤σ≤1);β=1表示施工单位严格按照法律法规和安全标准运行,不会因为施工单位安全管理原因导致安全事故。
假设2:政府监管部门履行强监管职责需要承担的监管成本为c1,若强监管过程中发现施工单位忽视安全管理,则对其实施处罚p,强监管下加强安全管理给政府带来公信力的提升l,施工单位在完成该项目后所获收益为rs。施工单位选取加强安全管理所需要的安全投入成本为cs1,监管部门的日常收入rg。若施工单位选取忽视安全管理所需要的安全投入成本为cs2。定义施工单位加强安全管理的额外支出为施工单位加强安全管理与忽视安全管理的成本差,即cs1-cs2。若发生安全事故,施工单位必须支付ds来处理后续工作,同时给政府监管部门带来公信力的损失n。政府监管部门履行弱监管职责需要承担的监管成本为c2。
基于上述假设与分析,构建政府监管部门与施工单位的演化博弈模型,得到的收益矩阵如表2所示。

表2 装配式建筑施工安全监管收益矩阵Table 2 Payoff matrix for construction safety supervision of prefabricated buildings
2 政府监管部门对施工单位动态安全监管的演化博弈分析
根据前述分析可知,政府监管部门应根据施工单位忽视安全管理的意愿来动态调整惩罚力度,参考刘伟等[14]、朱庆华等[15]研究成果,本文假设政府的惩罚力度与施工单位采取忽视安全管理策略的概率是非线性相关,引入非线性的动态惩罚函数p[(e1-β-1)/(e-1)],故政府监管部门和施工单位的博弈矩阵如表3所示。

表3 装配式建筑施工安全非线性动态监管收益矩阵Table 3 Payoff matrix for non-linear dynamic supervision on construction safety of prefabricated buildings
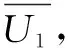
U11=β(rg-c1+l)+(1-β)(rg+
p[(eβ-e)/(1-e)]-c1-σn)
U12=β(rg-c2)+(1-β)(rg-c2-σn)
政府监管部门策略的复制动态方程F(α)为:
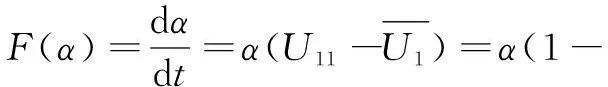
复制动态方程对y求偏导得:
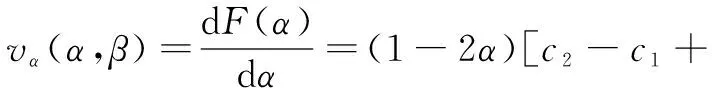
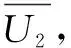
U21=α(rs-cs1)+(1-α)(rs-cs1)
U22=α(rs-p[(eβ-e)/(1-e)]-
cs2-σds)+(1-α)(rs-cs2-σds)
施工单位的复制动态方程F(β)为:
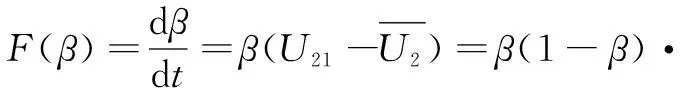
复制动态方程对x求偏导得
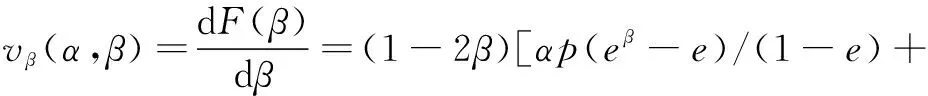
进一步得博弈系统的均衡点为
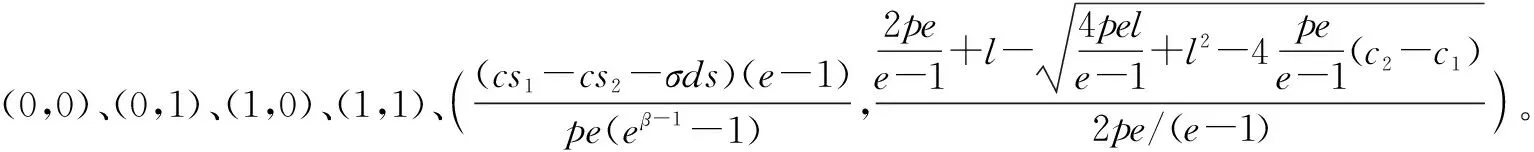
(1)
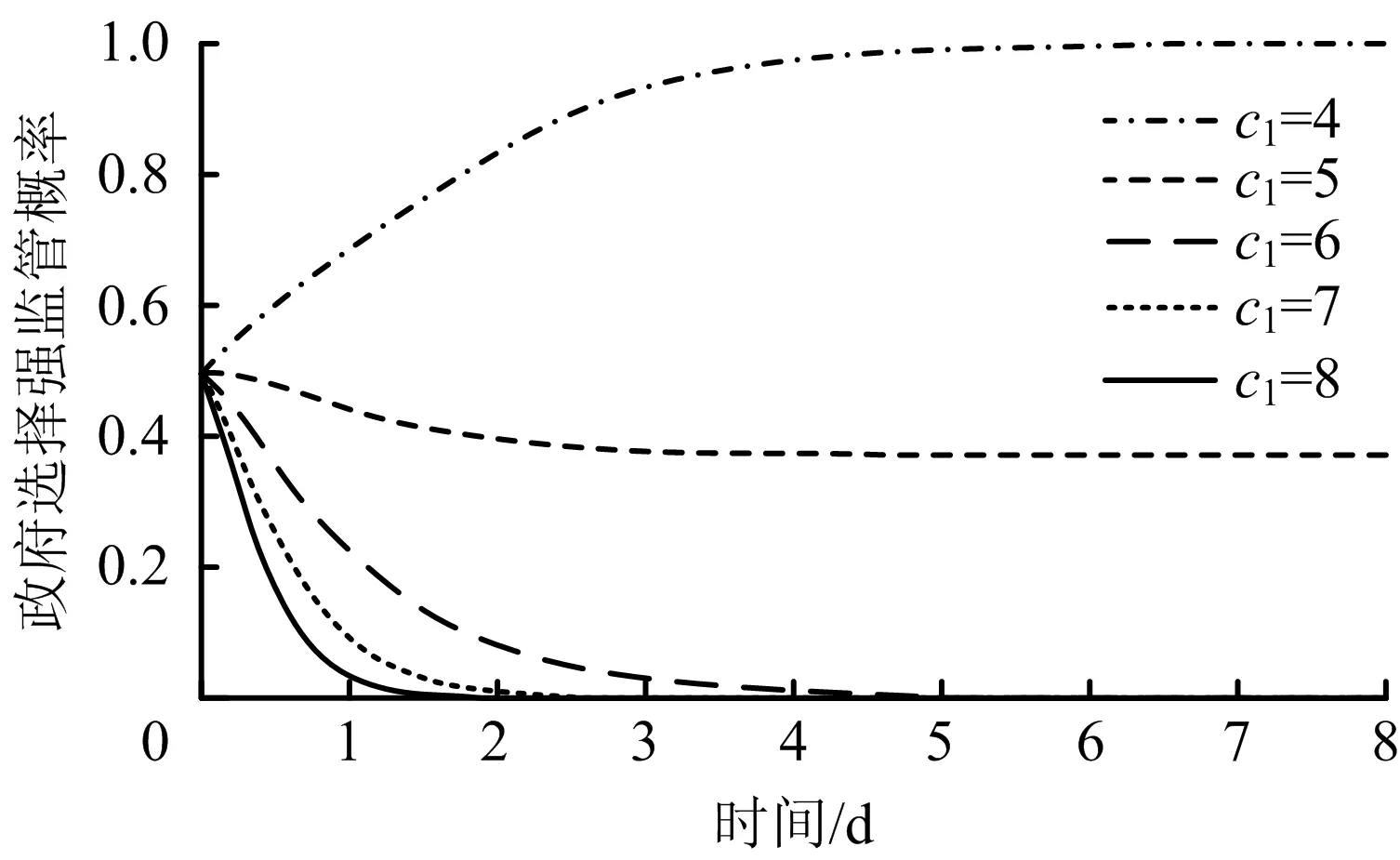
由式(1)可得系统雅可比矩阵的行列式和迹,若平衡点满足Det(J)>0和tr(J)<0这2个条件,则平衡点为演化动态过程的演化稳定策略,即ESS。该演化系统平衡点的稳定性分9种情形进行讨论,其中根据现实情况有已知条件:cs1-cs2>0、c1-c2>0、l 情形1:当cs1-cs2-σds<0且0 情形2:当cs1-cs2-σds<0且l 情形3:当cs1-cs2-σds<0且c1-c2>p时,系统最终收敛到演化稳定策略(0,1)。 情形4:当0 情形5:当0 情形6:当0 情形7:当cs1-cs2-σds>p且0 情形8:当cs1-cs2-σds>p且l 情形9:当cs1-cs2-σds>p且c1-c2>p时,系统最终收敛到演化稳定策略(0,0)。 9种情形下平衡点稳定性分析具体结果如表4所示。 表4 稳定性分析结果Table 4 Results of stability analysis 3.1.1 构建系统流图 考虑装配式建筑施工安全监管的实际情况,利用SD的仿真工具建立演化博弈模型,分析不同的博弈初始值对博弈演化过程的影响。依据政府与施工单位安全监管演化博弈模型,采用Vensim PLE软件构建双方演化博弈的SD模型,如图1所示。 图1 装配式建筑施工安全动态监管演化博弈的SD流图Fig.1 SD flow graph of evolutionary game for dynamic supervision on construction safety of prefabricated buildings 3.1.2 外部变量取值 外部变量主要包括政府监管部门的强弱监管成本、施工单位安全管理成本等,外部变量初值设定为:σ=0.3,c1=4,c2=2,p=5,cs1=5,cs2=3,rg=6,rs=6,ds=10,l=3,n=4。 SD模型仿真中,主要通过调整模型中辅助变量间关系以及外部变量取值来实现策略优化。依据前述分析,政府监管部门给予施工单位的惩罚p与其忽视安全管理的概率1-β并非简单的线性关系,而是呈抛物线关系。在施工单位加强安全管理意愿低的情况下,政府会加大惩罚力度刺激施工单位安全管理的积极性,当施工单位加强安全管理积极性已充分调动时,政府又会逐渐削弱惩罚力度。因此,本文引入指数型的非线性动态惩罚变量p[(e1-β-1)/(e-1)],代入外部变量初值进行仿真,结果如图2所示。 图2 动态监管策略下的博弈演化趋势Fig.2 Trend of evolutionary game under dynamic supervision strategy 此时外部变量的取值符合条件cs1-cs2-σds<0和0 3.3.1 出现安全事故概率σ敏感性分析 将忽视安全管理出现事故的概率σ依次设置为0.3、0.4,…,1,代入模型仿真模拟,结果如图3所示。当在情形1的状态下,逐渐提升σ的值,发现政府监管部门和施工单位均加快向理想策略(强监管,加强安全管理)演化。从图3可知,σ的改变对于施工单位的策略选择影响较大,加强施工安全管理的演化速率大于政府部门选择加强安全监管的演化速率。 图3 安全事故概率σ的敏感性分析Fig.3 Sensitivity analysis on probabilityof safety accidents 3.3.2 忽视安全管理惩罚力度p的敏感性分析 对忽视安全管理惩罚力度p进行敏感性分析,结果如图4所示。逐渐增大p值,政府监管部门和施工单位均加快向理想策略(强监管,加强安全管理)演化。由此可见,加大惩罚力度,则会削弱施工单位的投机行为,增大其加强安全管理施工的积极性。而与调整σ值不同的是,增大惩罚力度同样也大幅加强政府部门加强安全监管的积极性。这是因为σ值的改变只是加大了施工单位损失,但对政府的收益影响较小。但是,对施工单位的惩罚值p也是政府部门的收入,故增大惩罚力度也可以大幅增加政府强监管策略选择的积极性。 图4 惩罚力度p的敏感性分析Fig.4 Sensitivity analysis of punishment intensity 3.3.3 施工单位安全管理成本差的敏感性分析 施工单位安全管理成本对于其策略选择有着不可忽视的作用,通过增大cs1的值,加强安全管理与忽视安全管理的成本差增大,其对施工单位策略选择影响的仿真结果如图5所示。cs1的值从5逐渐增大到12,则系统的状态从情形1转化到情形4再到情形7,策略选择从加强安全管理到没有演化稳定策略再到忽视安全管理,仿真结果与理论分析一致。当施工单位选择加强安全管理时,若此时成本过高,则会增加施工单位投机行为产生的概率,促使施工单位不惜冒险承担安全事故后的损失以及政府的惩罚措施。 图5 施工单位安全管理成本差敏感性分析Fig.5 Sensitivity analysis on cost difference in safety management of construction organization 3.3.4 政府强、弱监管成本差的敏感性分析 同理,通过逐渐增大c1的值,政府强、弱安全监管的成本差增大,其对政府策略选择影响的仿真结果如图6所示。c1的值从4逐渐增大到8,则系统的状态从情形1转化到情形2再到情形3,策略选择从强监管到弱监管,仿真结果与理论分析一致。对于政府部门来说,强监管耗费的人力物力财力过多时,若没有取得良好的收益,如政府公信力(l)的提升,惩罚收入的增加等,可能会削减其强监管的积极性。 图6 政府强弱监管成本差敏感性分析Fig.6 Sensitivity analysis on cost difference between strong and weak government supervision 通过上述仿真可知:装配式建筑施工安全动态监管机制下,博弈双方在不同的情形条件下具有不同策略的稳定性,故可依据SD模型中变量取值对博弈主体行为策略的影响机理,调整参数取值,使装配式建筑施工安全监管效果达到理想的状态。 1)政府监管部门监督强度受强、弱监管成本、惩罚力度、施工单位忽视安全管理下安全事故发生概率等变量影响。相对于依靠投机行为降低安全事故发生概率σ来进行安全管理,加大惩罚力度来减少安全事故发生更加合理有效。安全监管的重点在于施工过程的监管而非事后追责,政府在提高监管部门和施工单位安全合规意识的同时,应增加日常安全监督的频次和出现安全事故时的惩罚力度。 2)施工单位落实加强安全管理措施受加强安全管理与忽视安全管理成本差、预期事故损失、施工单位忽视安全管理下安全事故发生概率等变量影响。仿真结果显示,通过增大政府对施工单位忽视安全管理的惩罚力度或加大安全事故施工单位损失均可以促进施工单位加强安全管理。同时,安全管理成本是影响施工单位策略选择的重要因素,政府可以通过财政增拨、补贴、税收减免等方式降低施工单位安全管理投入负担,从而有效提高施工单位加强安全管理的概率。总体来说,非线性动态监管策略对施工单位安全行为有很好的促进效果。 1)运用演化博弈理论和SD仿真,构建政府与施工单位装配式建筑施工安全的非线性动态监管演化博弈模型,通过对模型求解,求得演化博弈的5个博弈局部均衡点。借助FRIENDMAN理论分别研究系统5个局部稳定点在不同条件下的稳定性,在非线性动态监管机制下,考虑9种情形下双方博弈模型稳定均衡解的存在情况。提出装配式建筑施工安全的非线性动态监管策略,可以有效避免装配式建筑施工安全事故的发生。 2)在Vensim PLE软件环境下对博弈演化进程进行仿真,研究不同条件下博弈双方的演化博弈趋势。仿真结果发现,适当提高政府对施工单位忽视安全管理的惩罚力度,可以有效促进双方向最理想策略(强监管,加强安全管理)演化。同时政府可提高补贴等措施降低施工单位安全管理投入负担,从而降低施工单位的安全管理成本,可以促进施工单位加强安全管理的积极性,并为提高自身形象,扩大政府公信力打下基础。 3)在非线性动态惩罚方案下,政府对于施工单位的惩罚与忽视安全管理的意愿呈非线性关系。这更加符合监管的实际,具有现实意义。在施工单位忽视安全管理意愿最强时,通过大幅增加惩罚力度可以显著提高施工单位加强安全管理的积极性;而当施工单位重视安全管理主观意愿较强时,政府从平衡监管成本和监管效率角度出发,可以逐渐降低监管力度。
3 装配式建筑施工安全动态监管的SD仿真
3.1 演化博弈的SD建模
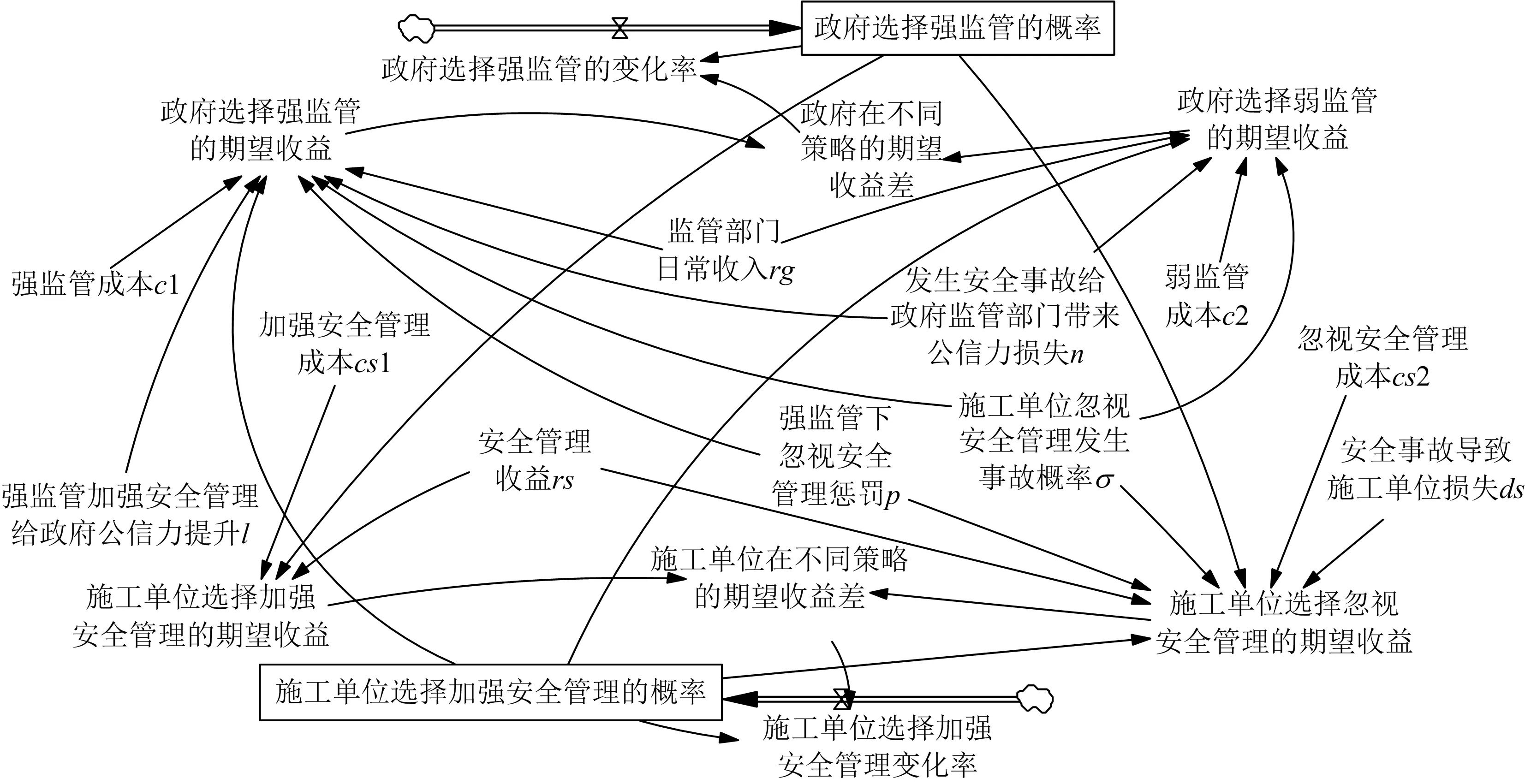
3.2 动态监管策略的仿真
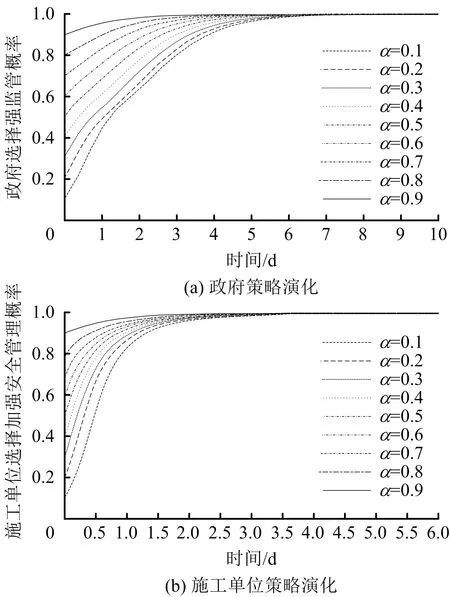
3.3 外部变量的仿真
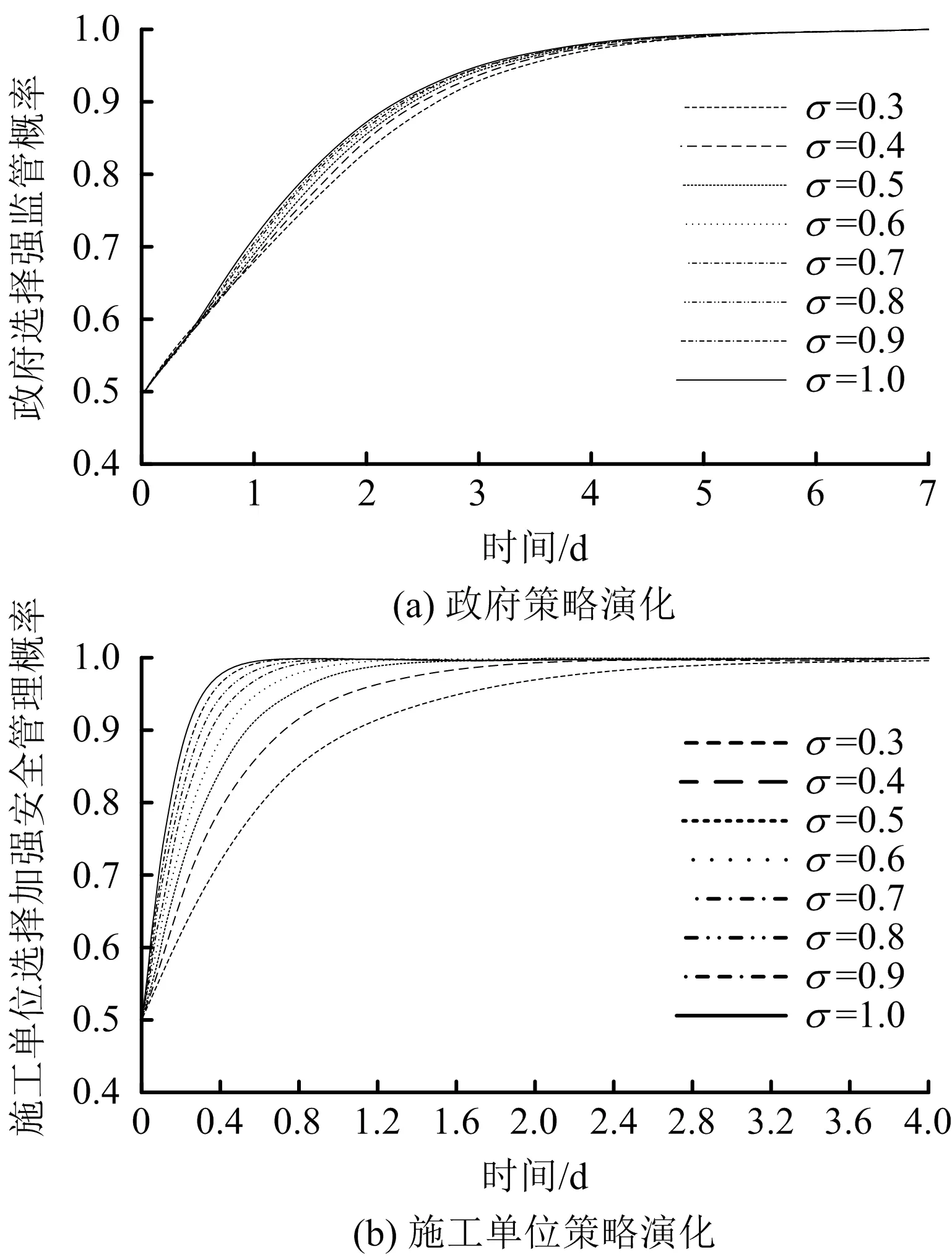
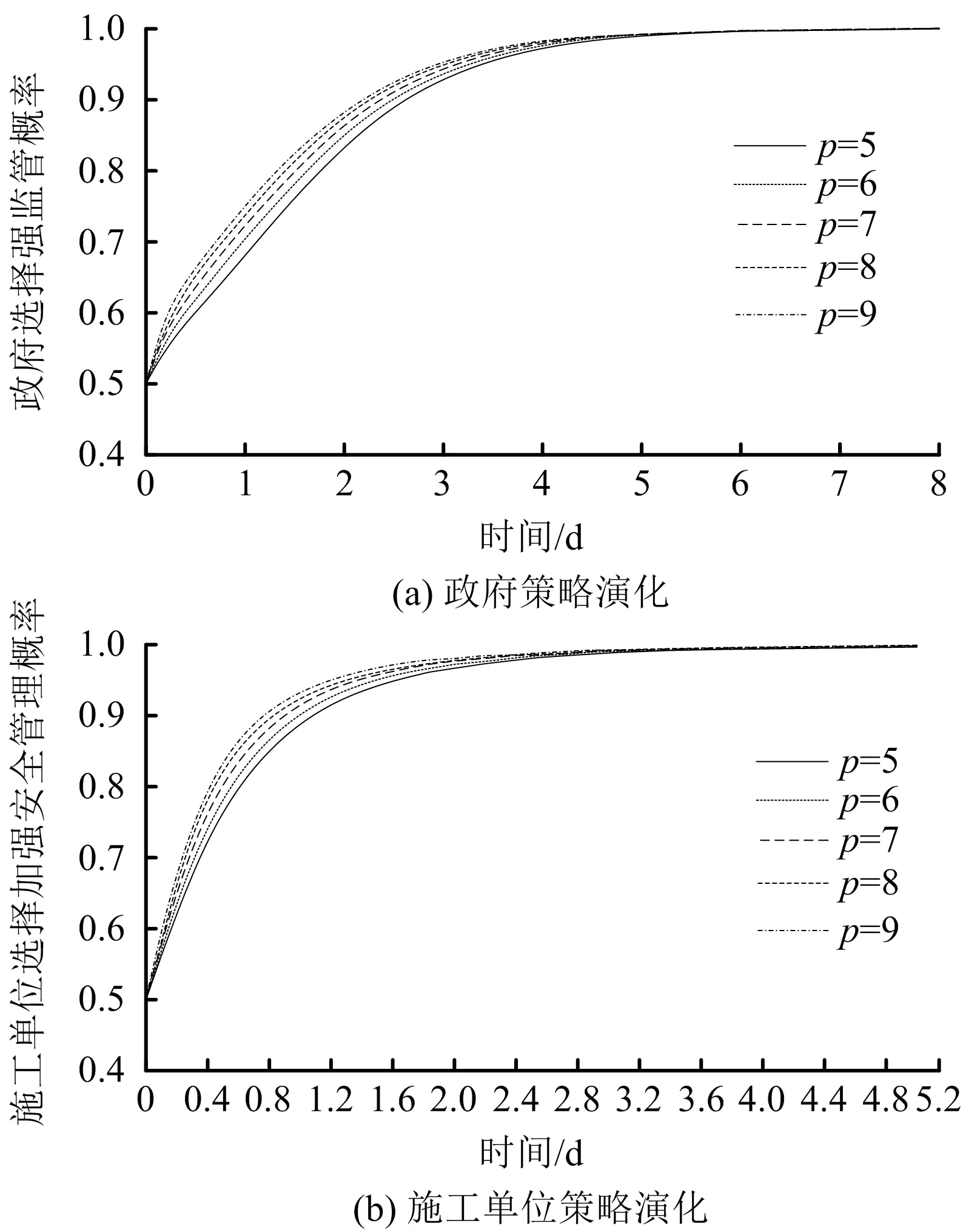
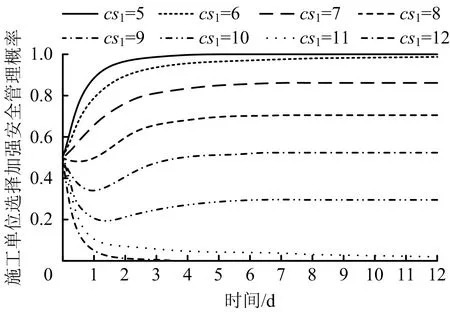
3.4 仿真结果分析
4 结论

