管道环焊接头残余应力及氢扩散模拟研究*
帅 健,谢 丹,,王 伟,3,李海川
(1.中国石油大学(北京) 安全与海洋工程学院,北京 102249;2.国家石油天然气管网集团有限公司 西气东输分公司,上海 200122;3.中海油能源发展公司,北京 100027)
0 引言
随着人们对能源的需求不断增长以及化石能源产生的环境污染等问题日益严重,对新能源的开发与利用已成为全球范围关注的焦点问题。氢气具有洁净高效等特点,已成为最有发展前景的新能源之一,管道输送被认为是大规模输氢最有效的方式[1-4]。现如今对于天然气管输技术,国内外已形成较为成熟的安全运营体系,但对于输氢管道还存在较多安全性问题亟待解决。不同于天然气输送,氢气的输送有其特殊性,氢分子会通过表面吸附、解离等一系列过程分解成氢原子进入金属材料内部[5-6],在焊接残余应力的作用下,氢原子会向应力集中区域扩散并聚集,当局部氢浓度达到一定值时很容易引起氢致裂纹的出现[7],从而导致管道失效,引发安全事故。因此,对管道焊接中产生的残余应力以及管线钢中的氢浓度分布进行预测和控制具有重要的理论意义和工程价值。
近年来,数值模拟技术越来越多地用于焊接残余应力以及氢扩散行为的研究。Mochizuki等[8]提出了1种二维轴对称模型来模拟计算管道对接焊接头的残余应力,但是轴对称假设使得该模型存在一定的局限性。Wu等[9]利用MSC-Marc软件建立了管道单道焊的三维模型来研究管道TIG焊接过程中应力变化,但是该模型将管道焊接接头简化为单道焊。蒋文春等[10]对焊接残余应力梯度下的氢扩散情况进行了模拟研究,但计算过程中将焊接接头作为均质材料处理。张体明等[11]考虑焊接残余应力和组织不均匀性,对煤制气螺旋焊管接头处的氢扩散过程进行了模拟研究。Zhao等[12]对X80钢螺旋焊管氢气输送过程中氢的动态扩散过程和最终浓度分布进行了数值研究。然而,这些研究都是将焊接过程简化为单层焊。针对管道环向焊接过程,尤其是多层焊接的模拟研究较少,对于多层焊接接头层间的残余应力分布并不清楚,以及不同焊接层的热输入量对残余应力和氢分布的影响分析也不多。
本文对管道环焊接头的3层焊接过程进行模拟,分析3层焊接接头层间的残余应力分布规律,并对焊接残余应力状态下的氢扩散行为进行模拟研究,阐明每层焊接过程的热输入量对氢分布的影响,从而为输氢管道的技术标准制定提供理论依据。
1 有限元模型的建立
1.1 有限元分析思路
针对残余应力作用下的氢扩散分析的数值计算过程分为3步:第1步,对焊接温度场进行计算;第2步,将温度场结果作为载荷导入焊接应力场的模型中进行耦合计算;第3步,将焊接残余应力作为氢扩散的预定义场进行氢扩散的顺次耦合计算。由于前期的温度场计算直接关系到后续的应力场和氢扩散的计算准确与否,因此,为了使热源尽量接近实际焊接热源,选用双椭球热源模型作为焊接热源[13]。
1.2 几何模型和网格划分
建立管道3层单道环向对接焊的三维实体模型,如图1所示。选取外径为114 mm、壁厚为11.13 mm的管道进行分析计算,考虑焊接热源对管道远端区域几乎不产生影响,用于计算的管段长度取500 mm。由于焊缝和近焊缝区受热源影响最大,将产生高温和较大的应力梯度,因此在距离焊接中心线200 mm范围内的网格划分相对细密,而离焊缝区和热影响区较远的位置受热源影响较小,采用相对稀疏的网格。

图1 有限元模型Fig.1 Finite element model
氢扩散分析模型的几何尺寸、网格划分以及单元节点编号与焊接温度场、应力场均保持一致。但需改变分析步类型为质量传递,选用三维八节点单元DC3D8。
焊缝开v型坡口,其几何形状如图2所示。其中壁厚T=11.13 mm,Rf=3 mm,Ro=2 mm,管段总长度L=1 000 mm,焊缝坡口角度θ=60°。

图2 焊缝的几何形状Fig.2 Geometric shape of weld
1.3 材料参数
在进行焊接模拟计算时,需要考虑材料性能参数随温度变化。假设管道母材与焊料的材料属性相同。材料性能参数随温度变化情况如图3所示[14]。其中,α为导热系数,W/(m·℃);cp为比热容,10 J/(kg·℃);k为线膨胀系数,×10-6℃-1;E为弹性模量,×109Pa;μ为泊松比,×10-2;σs为屈服强度,×107Pa。密度为7 800 kg/m3。
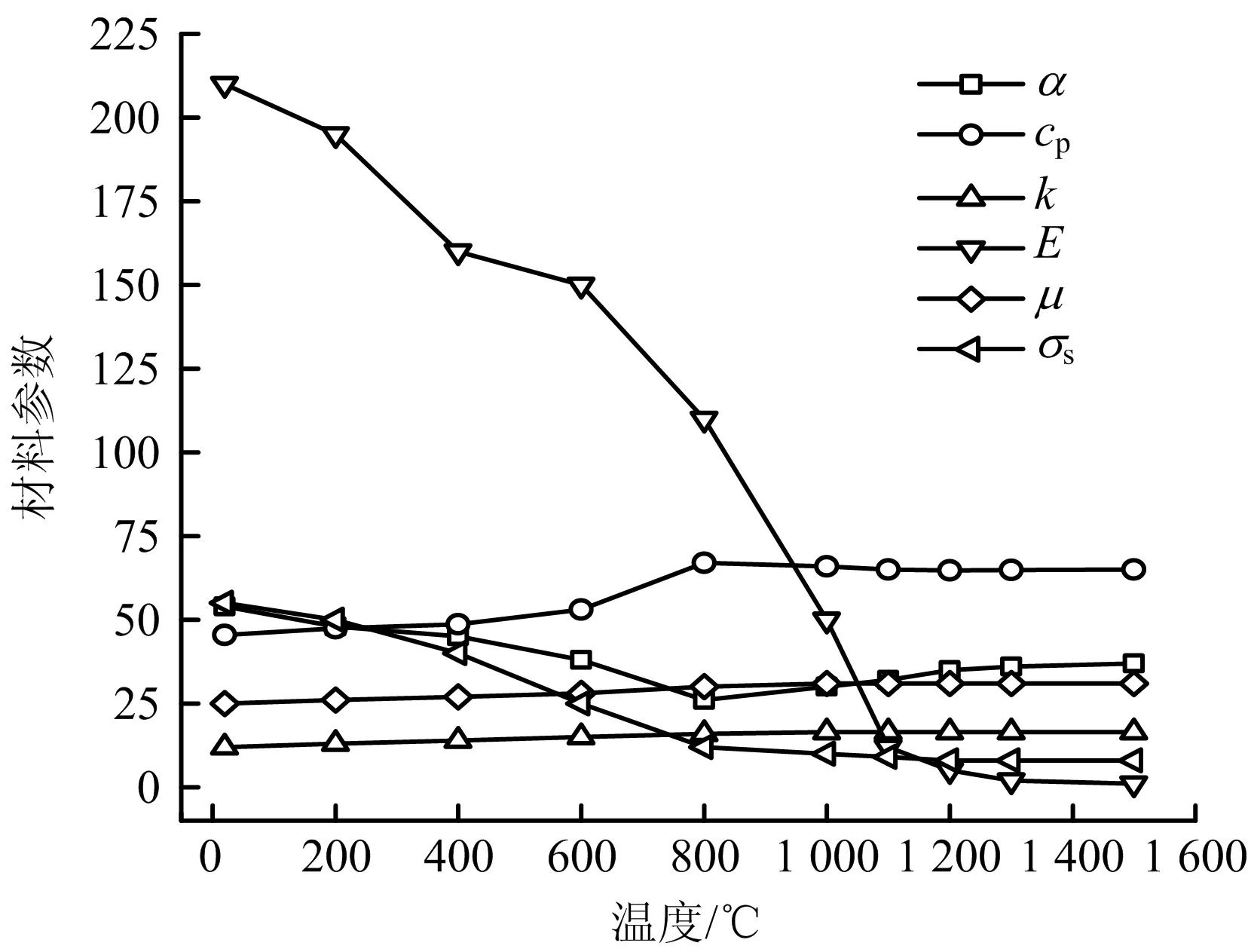
图3 材料性能参数Fig.3 Material performance parameters
在氢扩散分析中,管道焊接接头各部位的氢扩散参数采用表1所示的值[11]。

表1 焊接接头各区的氢扩散参数Table 1 Hydrogen diffusion parameters in each zone of welded joint
考虑焊接残余应力对氢扩散的影响,其应力梯度系数的计算方法如式(1)所示[10]:
(1)
式中:Kσ为应力梯度系数,N/m1/2;VH为氢原子在金属材料中的偏摩尔体积,取值为2 000.0 mm3/mol;R为气体常数,取8.3 J/(mol·K);T表示温度,℃;θZ表示绝对零度,℃。
1.4 边界条件
管道的初始温度取20 ℃,对焊缝接头的中心面施加对称约束,并进行绝热处理。对于管道的内外表面,考虑热辐射和对流换热的边界条件,对流换热系数取10 W/(m2·℃),热辐射率取0.85。
在应力场计算中,为了保证管道不会发生刚性移动,约束起焊点位置沿切线方向的位移,在远离焊缝处取2个节点固定。
在氢扩散分析中,表征边界条件的参数是氢活度φ,其计算方法如式(2)所示:
φ=C/S
(2)
式中:φ为氢气活度;C为原子氢浓度,%;S为原子氢溶解度,%。
考虑管输介质中的氢进入金属材料后的扩散行为,不考虑管道钢在冶炼及焊接过程中引入到金属材料中的氢,因此设定管道内表面的氢浓度为初始条件。氢以原子的形式扩散,当氢原子扩散至管道外表面时会结合成氢分子逸出,因而不考虑管道外表面的氢浓度。
1.5 模型验证
DENG等[15]曾通过试验方法对管道焊接接头的残余应力进行过测量,以DENG等的试验方案为参考依据,验证焊接模拟模型的正确性。根据文献中提供的参数建立模型,将有限元模拟结果和DENG的试验值进行对比,结果如图4所示,由图可以看出,通过有限元计算得到的轴向残余应力与试验测量得到的残余应力分布趋势基本一致,说明采用该有限元程序可以对管道焊接过程进行仿真模拟。

图4 残余应力模拟值与测量值对比Fig.4 Comparison of simulated and measured residual stress
2 残余应力分析
管道焊后的等效残余应力云图如图5所示。管道焊接完冷却后在焊缝及其附近区域产生严重的应力集中现象,其最大等效应力值为618 MPa,已超过材料的屈服强度。等效应力主要集中在第2层与第3层焊接相邻位置以及整个第3层焊缝区域,外表面的等效应力值大于内表面。

图5 等效残余应力云图Fig.5 Cloud diagram of Mises residual stress
距焊接起点90°位置焊缝中心的轴向应力沿径向路径的变化趋势图如图6所示,从图6中可以看出,轴向应力沿管道厚度方向呈波动变化趋势,层与层焊接交界位置为轴向应力波动变化的拐点。在焊缝区域的内表面形成轴向拉伸应力,在外表面形成轴向压缩应力。
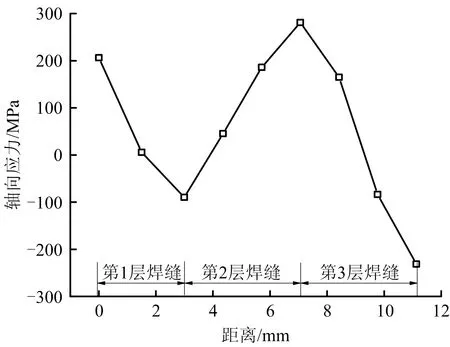
图6 轴向应力沿径向路径变化Fig.6 Change of axial stress along radial path
距焊接起点90°位置焊缝中心的环向应力沿径向路径的变化趋势图如图7所示,从图7中可以看出,焊缝中心的环向应力在管道厚度方向上都呈拉应力状态,最大值分布在第2层焊缝与第3层焊缝交界位置,焊缝区域外表面的环向应力大于内表面。

图7 环向应力沿径向路径变化Fig.7 Change of hoop stress along radial path
通过对比焊缝区的轴向应力与环向应力发现,管道焊接接头的环向应力值远大于其轴向应力值,并且环向应力的变化梯度也大于轴向应力的变化梯度,说明在焊缝区域主要受环向应力的影响。
3 氢扩散分析
3.1 残余应力作用下氢浓度分布
在氢扩散分析中,影响氢扩散的应力为静水应力[16],其值为管道环向应力、轴向应力和径向应力的平均值。图8为距焊接起点90°位置焊缝中心的氢浓度和静水应力沿径向路径的变化曲线。从图8(a)中可以看出,焊缝中心的扩散氢浓度在管道径向方向上呈波动分布趋势,氢浓度最大值为0.058 3×10-6,位于第2层焊缝与第3层焊缝交界位置。如图8(b)所示,焊缝中心的静水应力在管道径向方向上分布与氢浓度分布趋势相似,在第2层焊缝与第3层焊缝交界位置存在静水应力最大值355 MPa。
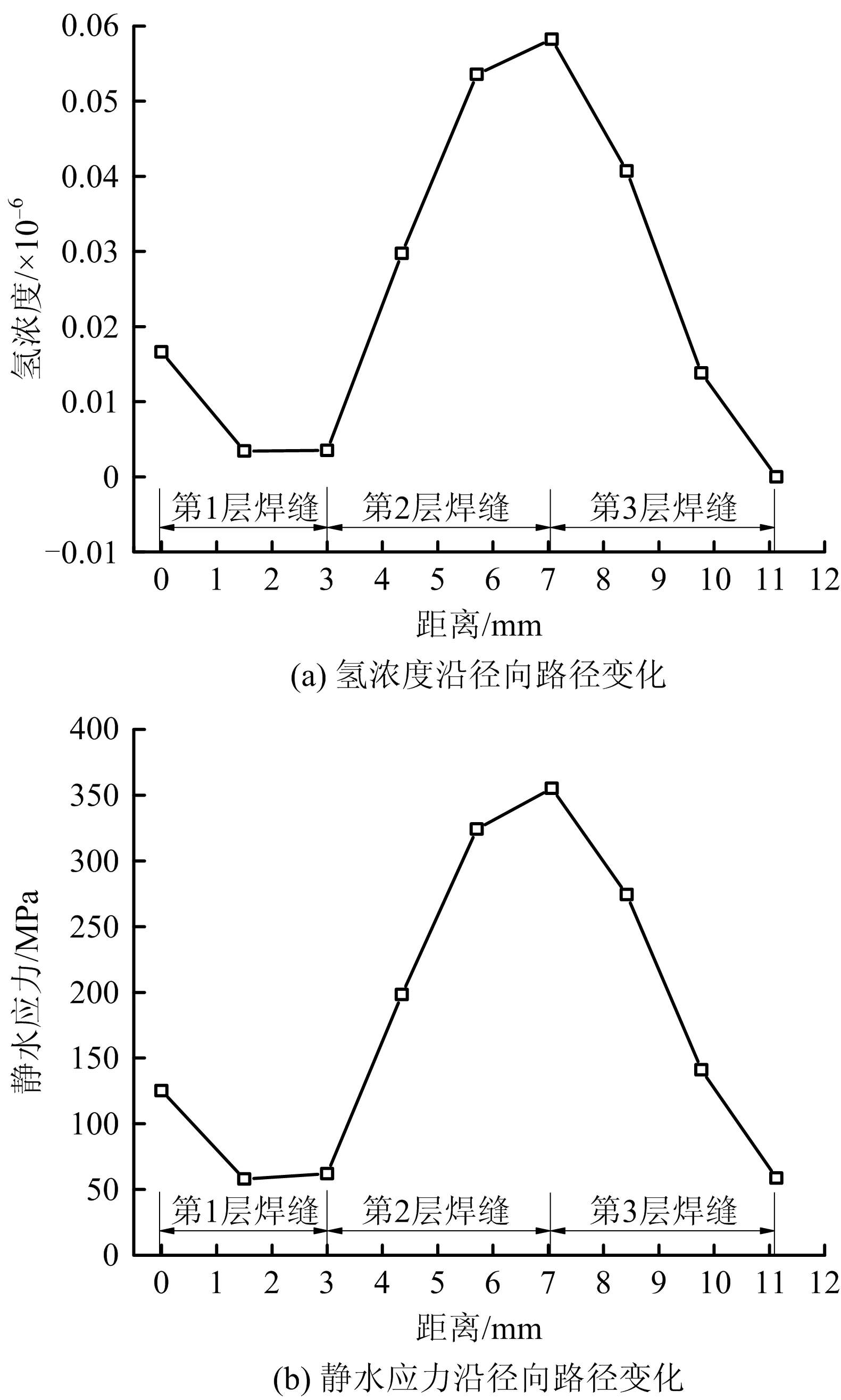
图8 氢浓度及静水应力沿径向路径变化Fig.8 Change of hydrogen concentration and hydrostatic stress along radial path
由此可见,氢浓度富集的部位与静水应力集中的区域相对应。焊接残余应力促进了氢在管道钢中的聚集,其诱导氢原子向应力集中区域扩散。
3.2 无残余应力作用下氢浓度分布
在无残余应力状态下,氢扩散的驱动力为浓度梯度。由于管道内、外表面边界条件的设定使管道内、外壁之间存在浓度差,所以氢扩散方向为从管道内表面区域向管道外表面区域扩散。
单独取某1区域焊缝单元的氢浓度分布云图,如图9所示,从图中可以看出,氢浓度值从管道内表面至外表面逐渐减小。

图9 焊缝单元氢浓度分布云图Fig.9 Cloud diagram of hydrogen concentration distribution in weld element
任取1轴截面,其氢浓度分布云图如图10所示,从图中可以看出氢浓度沿管道轴向方向呈均匀分布状态,管道母材区的氢浓度高于焊缝区,这主要是因为扩散氢在母材区的溶解度最大。

图10 管道轴截面氢浓度云图Fig.10 Cloud diagram of hydrogen concentration on pipeline axial section
3.3 2种状态下氢扩散对比分析
从图11中可以看出,有、无焊接残余应力状态下,焊缝中心的氢浓度分布存在明显差异。当不考虑残余应力时,焊缝中心的氢浓度最大值位于管道内表面,其最大值为初始浓度值0.016 6×10-6,并且从管道内表面至外表面氢浓度值逐渐降低。当存在残余应力时,焊缝中心的氢浓度分布更加集中,此时氢浓度最大值为0.058 3×10-6,出现在第2层焊缝与第3层焊缝交界处。由此可以得到,当存在焊接残余应力时,焊缝区中氢浓度最大值较无残余应力状态下增加了约3.5倍。此外,焊接残余应力对氢扩散的影响作用大于浓度梯度的影响。

图11 氢浓度分布对比Fig.11 Comparison of hydrogen concentration distribution
4 不同焊接层的线能量对氢扩散的影响
4.1 填充焊线能量的影响
保持打底焊、盖面焊的线能量不变,不同填充焊线能量下焊缝中心处的氢浓度沿径向路径的变化曲线如图12所示。由图12可以看出,焊缝中心氢浓度分布随填充焊线能量的增加呈减小的趋势。3种焊接线能量下的最大氢浓度值分别0.058 3×10-6、0.056 7×10-6和0.055 7×10-6,即填充焊线能量越高,焊缝中心的氢浓度最大值越小。
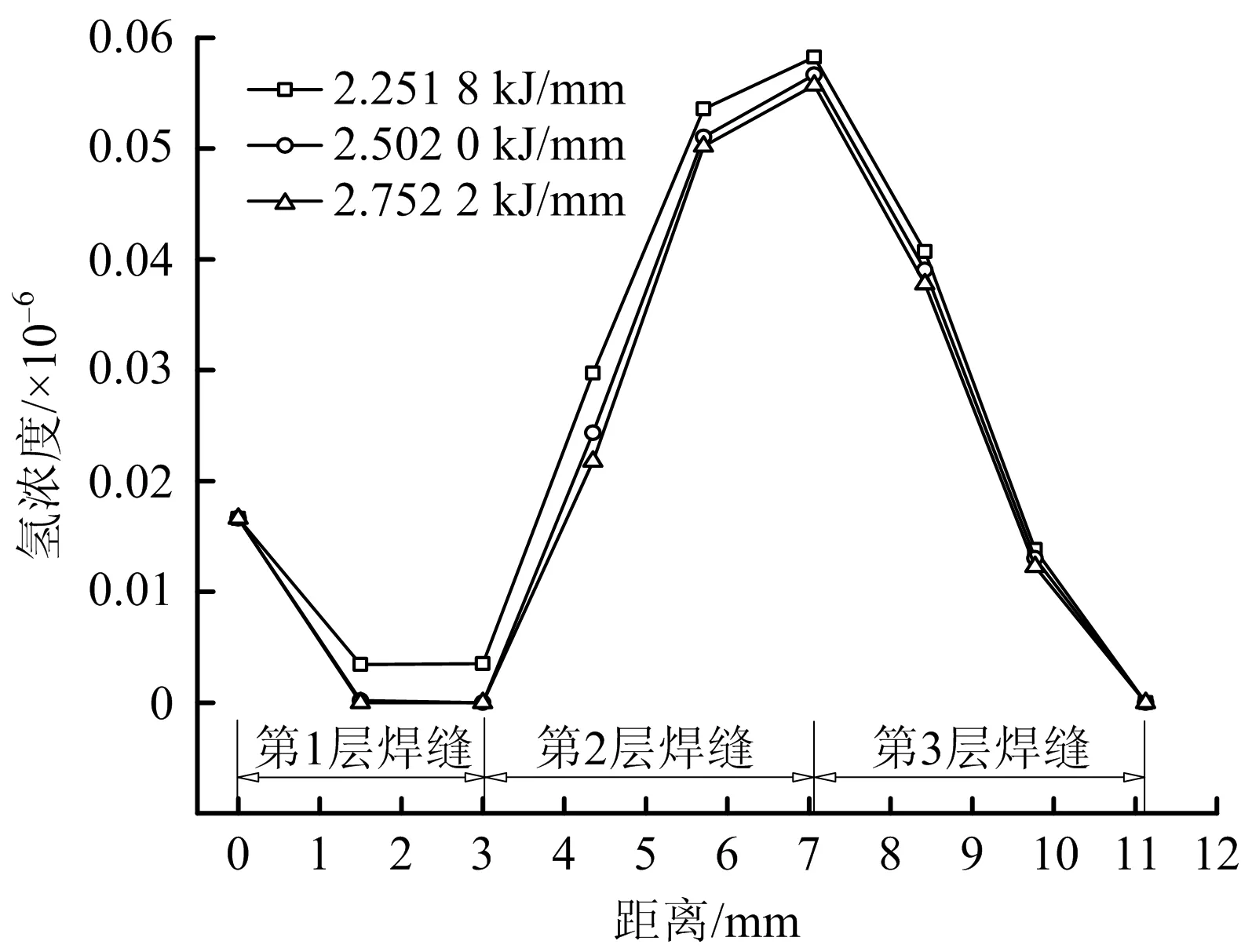
图12 不同填充焊线能量下的氢浓度分布Fig.12 Distribution of hydrogen concentration under different filling welding line energies
4.2 盖面焊线能量的影响
保持打底焊、填充焊的线能量不变,不同盖面焊线能量下焊缝中心处的氢浓度沿径向路径的变化曲线如图13所示。由图13可以看出,盖面焊线能量越低,焊缝中心氢浓度最大值越小。在焊接线能量分别为2.502,2.224,1.946 kJ/mm时,焊缝中心的氢浓度峰值分别为0.060 4×10-6、0.058 2×10-6和0.05×10-6。第1层焊缝和第2层焊缝区域的氢浓度都随着盖面焊线能量的降低而减小,并且氢浓度变化梯度较大。在第3层焊缝区域中,盖面焊线能量的改变几乎对氢浓度的分布不产生影响。
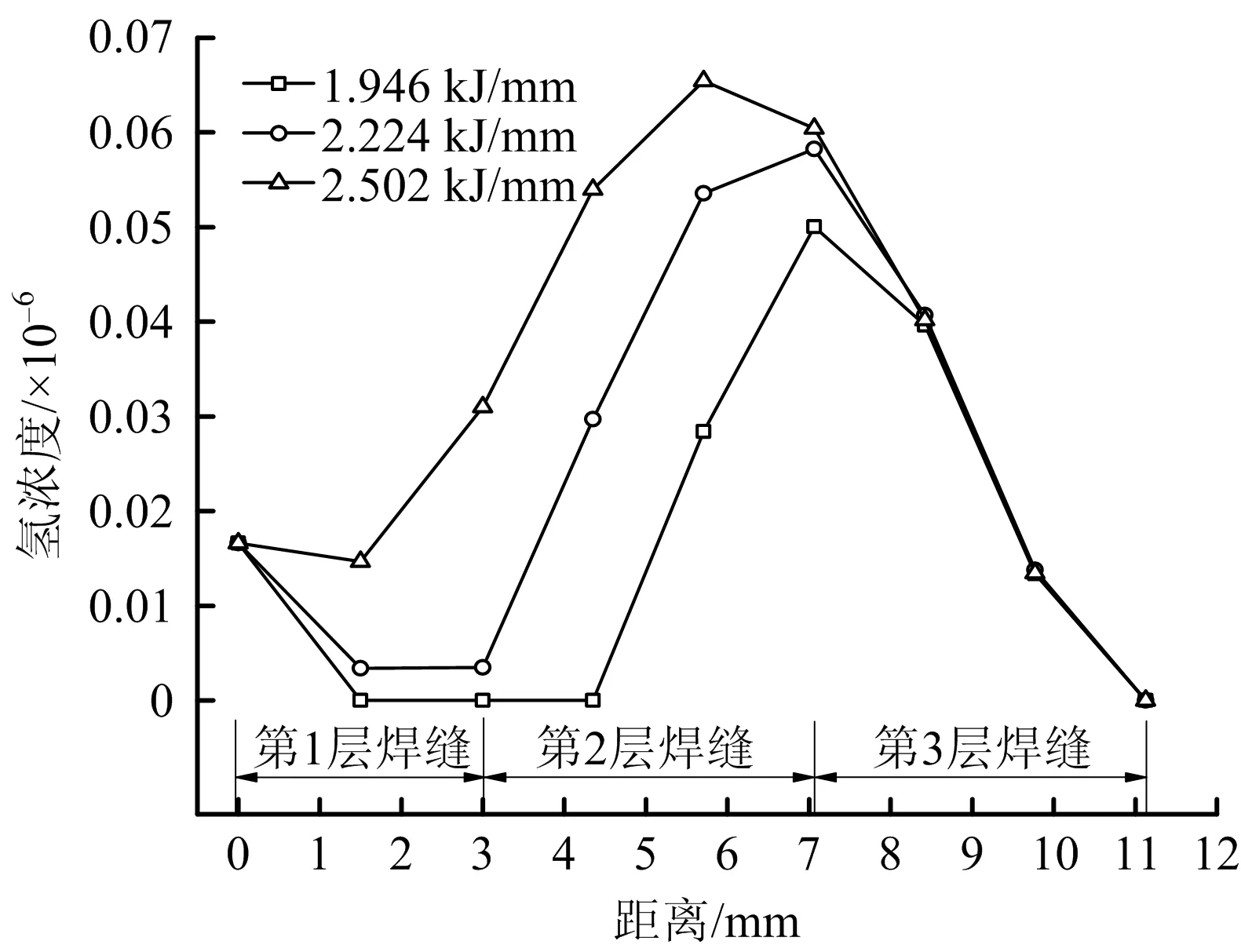
图13 不同盖面焊线能量下的氢浓度分布Fig.13 Distribution of hydrogen concentration under different cover welding line energies
4.3 打底焊线能量的影响
保持盖面焊、填充焊的线能量不变,不同打底焊线能量下焊缝中心处的氢浓度沿径向路径的变化曲线如图14所示,由图中可以看出,不同打底焊线能量在第一层焊缝区域的氢浓度分布差异很小。

图14 不同打底焊线能量下的氢浓度分布Fig.14 Distribution of hydrogen concentration under different priming welding line energies
5 结论
1)管道焊接完成后,焊缝及其附近区域的最大等效应力值为618 MPa,已超过材料的屈服强度,外表面的等效残余应力大于内表面。在焊缝区域的内表面产生轴向拉应力,在外表面产生轴向压应力,整个焊缝区都受到环向拉应力作用,且三向应力中环向应力最高,第2层焊缝与第3层焊缝交界处为应力最集中区域。
2)焊接残余应力状态对焊接接头的氢浓度分布存在显著影响。存在焊接残余应力情况下,氢浓度分布与静水应力分布状态一致,都集中分布在第2层焊缝和第3层焊缝相邻区域,其最大氢浓度值较无残余应力状态下高约3.5倍,且焊接残余应力对氢扩散的影响作用大于浓度梯度的影响。
3)在实际焊接过程中,在焊接工艺标准允许的范围内适当地提高填充焊线能量或者降低盖面焊线能量可有效降低焊接接头氢浓度富集程度,从而降低氢致裂纹敏感性,并且盖面焊线能量对氢扩散的影响作用大于填充焊线能量的影响。

