情景-应对模式下考虑软时间窗的高铁应急资源调度优化*
汤兆平,聂 欣,王振宇,孙剑萍
(华东交通大学 交通运输工程学院,江西 南昌 330013)
0 引言
近年来,高速铁路迅速发展,运输里程占铁路总里程的25.3%,客运量占铁路总量64.4%[1]。高速铁路具有运行速度快、运行密度大及长大隧道和高架多等特点,外加大量自主研发的新设备、新技术投入运用,使得高铁突发事件呈现种类多、影响大的特征,给应急救援带来新的挑战。因此,研究应急资源快速、高效调配是提升高速铁路应急处置水平的关键。
部分学者针对突发事件应急资源的调配优化进行研究,并取得一定成果。耗时最少是指整个配送任务的时间最短,是应急资源调度考虑的核心因素。在考虑救援时间最优条件下,还应考虑出动规模及救援成本等其他因素,因此学者将最小费用[2]、救援公平性[3-4]等影响因素纳入考虑范围,构成多目标决策模型,以解决最优化应急调度问题,提升应急资源调度能力。
突发事件的不可预测性、突发性,以及信息获取的缺失性和多变性,导致应急管理决策主体缺乏足够准确的信息来制定救援方案,使铁路应急救援过程中参数(如各事故点资源需求量、资源调度时间、救援成本等)存在不确定性。学者从需求不确定性、灾情动态变化、灾情情景分析等方面对资源调度进行研究:Liu等[5]针对需求和运输时间的不确定性,考虑山区灾后抗震救灾过程中特殊环境条件,提出灾后抗震救灾物流随机模型;汤兆平等[6]针对铁路突发事件发生后应急资源的不确定性,通过比较模糊评价和熵权的灰色关联理想法,得出受灾点的救援优先级;王飞跃等[7]引入区间数描述物资需求量和物资运输时间的不确定性,并以应急物资分配的经济性、时效性和公平性为目标,建立多目标线性区间规划模型;Sun等[8]为研究救援效率最高和事故损失最小,考虑需求的不确定性,提出救援决策响应时间最优的双目标鲁棒优化模型;任斌等[9]运用前景理论研究需求不确定性问题,构建应急物资需求动态调整模型,以保障应急资源需求预测的合理性。
现有文献大多针对公共突发事件的应急资源调度优化问题进行研究,部分针对铁路突发事件应急资源调度优化问题进行讨论,却忽略高铁运行环境特点、突发事件特点及应急情景的分析。本文考虑高速铁路突发事件发生后应急资源需求的不确定性,以“情景-应对”模式为基础,通过对事故情景集进行分析计算,预测得到应急资源需求量,引入“软时间窗”概念,构建以超时惩罚成本、资源运输成本和救援点固定出动成本3者之和最小化为优化目标的应急资源调度模型,为高铁应急救援部门的科学、高效决策提供理论依据。
1 高铁突发事件情景分析
情景分析是基于未来事件的不确定性无法避免,但未来事件的某些方面是可预测的[10]。在应急管理领域,情景分析可作为评估应急资源需求以及确定应急资源配置和调度的基础。
1.1 “情景-应对”模式下高铁应急处置流程
“情景-应对”模式的思路是通过改变情景集中的要素值实现情景变化,根据突发事件具体情景信息进行相似度计算,为优化决策提供重要参数。具体应急处置过程包括事件报告、情景要素分析、相似度计算、情景应对学习、资源调度优化以及应急终止,如图1所示。

图1 “情景-应对”模式下的高铁应急处置流程Fig.1 High-speed rail emergency response process under the “scenario-response” model
1.2 高铁突发事件情景要素提取与分析
情景要素作为“情景-应对”模式研究的重要基础,合适与否直接关系情景集的实用价值。高速铁路特征主要表现为客运列车运行密集、列车速度快和高架线路及长大隧道多,需要重点分析乘客要素、天气环境和地理环境要素。此外,需要对设备的相关要素进行提取。本文根据高铁突发事件特点和发生机理,将情景集要素分为2级,1级要素包括事件、乘客、设备等7种类型;2级要素包括事件名称、事故类型、受伤人数等26种具体指标。
情景集表示采用三元组表达式进行描述,如式(1)所示:
Scenario(F,M,U)
(1)
式中:F表示情景集的2级情景要素;M表示应急解决方案情景要素;U表示执行解决方案后的效果情景要素。
1.3 突发事件情景要素相似度计算
目标情景与当前情景相似度主要考虑情景要素的局部相似度和情景的全局相似度2方面。其中,局部相似度利用不同算法对所包含的枚举型、数值型、区间型、字符型和模糊型要素进行相似度计算;全局相似度考虑要素值完全和要素值不完全2种情况。
1)枚举型要素。包括事件类型、事件原因、事故响应等级、列车种类、天气、事故地点、资源类型等2级要素,当2个要素值相同时取其相似度为1,反之为0,如式(2)所示:
(2)
式中:Tf为目标情景第f个2级要素的值;Cmf为第m个情景中第f个2级要素的值。
2)数值型要素。包含事件时间、经济损失、受影响乘客数量、脱轨车厢数、列车脱轨最远距离等2级要素,此类要素采用基于海明距离公式[10]计算属性间的相似度,如式(3)所示:
(3)
式中:δ,λ分别为情景集中要素f取值范围的最大值和最小值。
3)字符型要素。包括事件名称、救援方案、存储位置等通过字符串进行描述的要素。假设Ωf={ε1,ε2,…,εu},Ωmf={γ1,γ2,…,γv}为2个不同情景要素的集合表示,则Ωf与Ωmf之间的相似度定义如式(4)所示:
(4)
4)区间型要素。高铁突发事件发生后,受灾点的旅客伤亡人数、车辆脱轨数等受灾信息无法得到准确数值,只能得到1个区间值,用式(5)计算数值和区间数之间的相似度:
(5)

5)模糊型要素。利用三角模糊数表示模糊型要素,并采用Wasserstein距离式演化的方法[11]计算相似度,如式(6)所示:
(6)
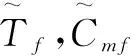
6)情景全局相似度计算。情景全局相似度计算建立在局部相似度计算基础之上。根据数据类型多样、部分数据缺失等实际问题,需要先通过比较情景之间所包含的情景要素,对其结构相似度进行计算。情景T与Cm之间结构相似度计算主要包括以下4个步骤:①情景T与Cm的所有非空集合分别记为ΩT和ΩCm。②ΩT和ΩCm的交集为Ω1=ΩT∩ΩCm和并集为Ω2=ΩT∪ΩCm。③将各要素权重值累加计算得到交集Ω1和并集Ω2所有要素的权重之和分别为WΩ1和WΩ2。④情景T与Cm的结构相似度计算如式(7)所示:
(7)
计算2个情景之间的全局相似度,需要综合考虑2者之间的结构与要素相似度,借鉴结构相似度算法[12]得到全局相似度计算公式,如式(8)所示:
(8)
式中:sim(T,Cm)为情景集中的情景T与目情景Cm的总体相似度值;ϖc为第c个1级要素的权重;sim(Tf,Ccf)为目标情景T的1级要素c下第f个2级要素与情景集中C情景的1级要素c下第f个2级要素的局部相似度;ϖcf为1级要素c下第f个2级要素指标权重;N为1级要素的个数;Mc为1级要素c下2级要素个数。
1.4 情景-应对下资源需求量的预测


(9)
式中:Xk为源情景中k类资源的需求量;sim(Tf,Cf)为情景T与源情景第f个元素相似度。
2 情景-应对模式下应急调度模型构建
2.1 模型假设
情景-应对模式下应急调度模型构建需要作如下3个假设:
1)已知突发事件的受灾点位置、备选救援点位置及资源存储量。
2)假设最佳救援时间为90 min内。
3)救援点出动时间为30 min,救援列车按规定速度匀速行驶至受灾点。
2.2 模型基础
模型中{S1,S2,…,Si}为备选救援点集合,i∈I;E为受灾点;K为救援点应急资源类型集合,k∈K。模型参数及其定义见表1。

表1 模型参数及其定义Table 1 Parameters and definitions of model
2.3 模型建立
高铁突发事件发生后,时间成为应急救援的关键因素。在以往研究中,学者引用“硬时间窗”对时间进行约束,即一定要在规定时间内到达,否则视为无效救援。但在实际救援中,应急资源的送达可能会超过预测时间窗限制。为解决“硬时间窗”的不足,本文引入“软时间窗”表达救援超时的惩罚成本。
“软时间窗”指因超出规定服务时间会产生相应的惩罚,但依然需要对客户进行服务,惩罚成本为迟到时间与惩罚系数之积[13]。选用升半柯西函数作为“软时间窗”的惩罚函数,如式(10)所示:
(10)
式中:α、β均为惩罚函数系数。
在实际救援中,应急资源不受限制的配置和调度会造成浪费[14]。为研究应急调度中时间和效益的问题,构建超时惩罚成本、资源运输成本和救援点固定出动成本3者之和最小化模型,如式(11)~(18)所示:
(11)
(12)
(13)
(14)
(15)
(16)
Δti≥0i∈I
(17)
(18)
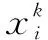
3 算例验证
以某高铁列车事故为例,事故造成现场线路中断,列车和线路设备遭到破坏,需要调度应急物资进行紧急救援及抢修。C={C1,C2,C3,C4,C5}为情景集中已知的5个源情景。源情景数据通过国内外历年铁路运营事故数据,并筛选国内外高铁客运事故案例得到,个别事故源情景选取与高铁运行环境相似的铁路旅客列车运行事故。当前事件为情景T,通过对事故现场基本信息进行总结分析,选取权重相对最高的16个2级要素作为决策参考,见表2。
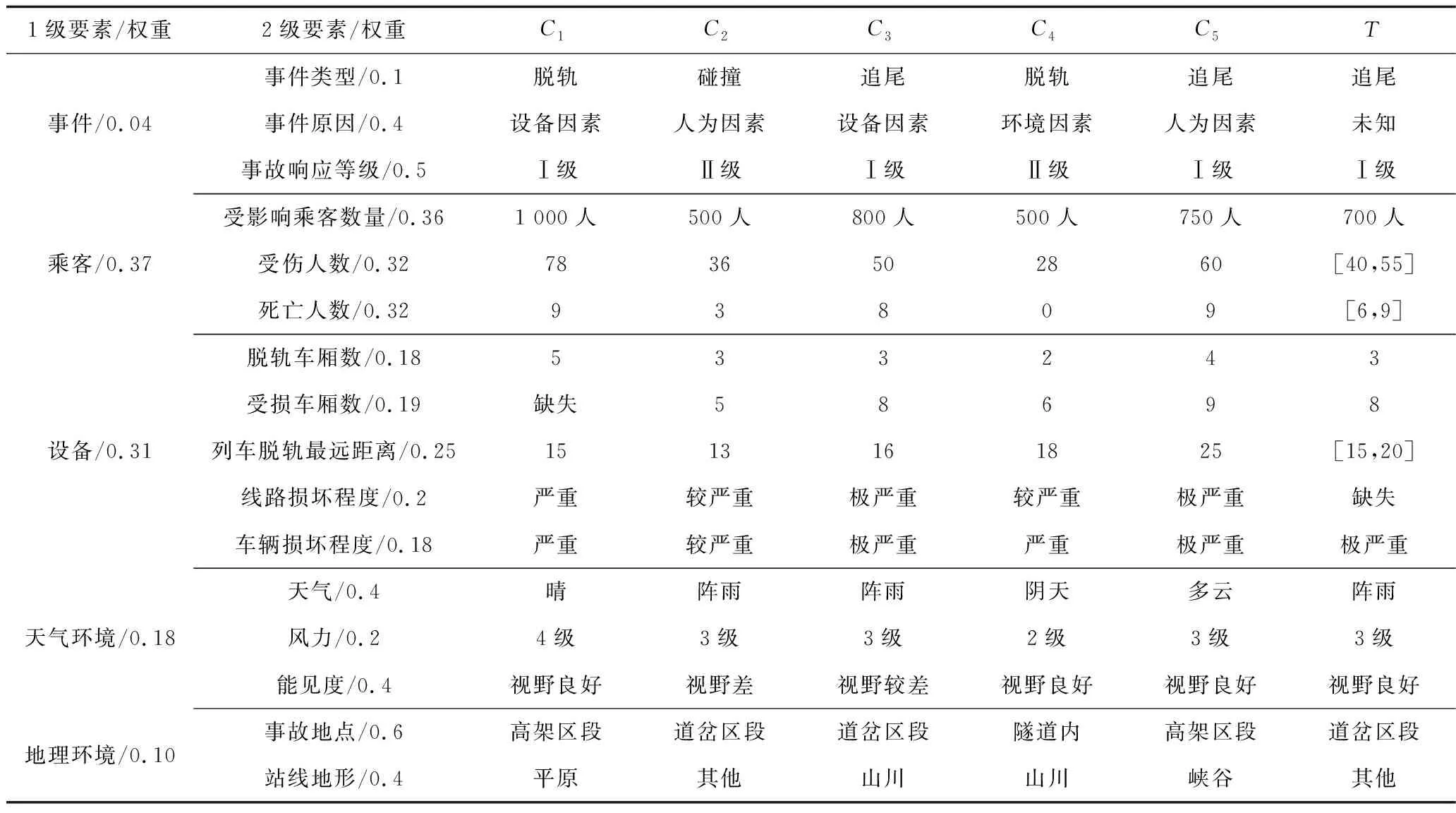
表2 情景要素取值Table 2 Scenario elements value table
利用层次分析法计算情景要素权重。参考相关文献[11,14]以及通过专家座谈会确定的各级情景要素,选取事故情景的5个1级要素即事件、乘客、设备、天气环境及地理环境,对各要素进行两两比较打分。邀请20名具有10 a以上相关工作经历的中级以上职称专家,及相关高校的专业技术人员对以上各情景要素进行权重值评价。5个1级要素的权重见表3,同理求得各2级要素权重。

表3 情景要素判断矩阵Table 3 Situational elements judgment matrix
建立情景要素判断矩阵,求得最大特征根λmax=5.43。将λmax=5.43、r=5和RI=1.12代入式(19)中计算,求得判断矩阵一致性比率CR=0.097<0.1,判断矩阵满足一致性检验:
(19)
式中:λmax为判断矩阵的最大特征根;r为矩阵阶数;RI为随机一致性指标,r=5时,查表得RI=1.12。
根据式(1)~(6),计算得到目标情景与情景集中各情景之间2级要素相似度,通过式(7)~(8)计算情景全局相似度见表4。

表4 T与情景集C的全局相似度Table 4 Global similarity between T and situation set C
由表4可知,C3与目标情景的相似度最高为0.87。因此,根据C3中的应急资源类型和数量对情景T的应急资源量进行预测。为验证情景预测方法的可行性,获取目标情景T的实际应急资源类型及数量,将实际使用量与各情景预测量对比。情景预测值在目标情景中的对比见表5。由表5可知,情景C3的应急资源使用量预测值更接近当前情景T的实际使用量(与其他情景的需求预测的平均误差比值相比分别降低了12.10%、10.66%、16.75%、10.30%),能够更准确预测出当前情景的应急资源需求,可为后续应急资源调度提供支撑。

表5 情景预测值在目标情景中的对比值Table 5 The ratio of the scenario predicted value in the target scenario
根据情景提取,受灾点所需的应急资源为轨道起重机、复轨器、食物饮用水、发电机组和急救车5种。救援点S1,S2,S3,S4,S5为受灾点提供应急资源,其中S1为1级救援点,其他为2级救援点。表6~9为情景T的具体信息。

表6 救援点Si的物资拥有量Table 6 Material possession of rescue point Si

表7 救援点Si到受灾点E的救援费用Table 7 Rescue cost table from rescue point Si to demand point E 万元

表8 受灾点E的物资需求Table 8 Material requirements table for disaster-affected point E

表9 救援点Si到受灾点E的距离Table 9 Distance and time from rescue point Si to demand point E
设置“软时间窗”函数中的系数α、β均为2,通过Matlab软件运用遗传算法求解模型。经过多次运行实验比较后,设置初始种群个体数目为30,迭代次数为200,交叉概率为0.7,变异概率为0.02。从结果中选取10组Pareto最优解做进一步分析。
为保证结果分析的有效性,对目标函数参数进行归一化[15]。采用式(20)对目标函数值进行归一化处理,得到Pareto最优解目标函数值:
(20)
式中:Z*为归一化后的目标函数值;Z为归一化前的目标函数值;Zmax为Pareto解群中的最大值;Zmin为Pareto解群中的最小值。
建立单目标函数的表达式,将归一化后的函数值通过式(21)计算得到最终优化结果:
(21)
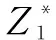
模型中2个子目标体现 “时间”与“效益”的关系,在实际救援中,需要找到2者的相对平衡。根据几种典型的权重系数对函数值进行计算,结果见表10。

表10 几种典型权重系数下Pareto最优加权结果Table 10 Pareto optimal weighting results under several typical weighting coefficients
由表10可知,遗传算法具有很强的鲁棒性和全局寻优能力,适合求解复杂的多极值优化问题和组合问题,具有求解速度快、获得的Pareto最优解不唯一等特点。所得Pareto最优解群可针对不同决策侧重点,设置子目标函数参数权重,利用归一化的方法进行计算分析,选择最适合的方案,为应急资源调度提供科学的依据。
为验证方法可靠性,选取a1=0.25,a2=0.75,利用Matlab调用Cplex求解器对模型进行求解比较,Cplex求得结果为34.5万元,遗传算法求解得到的Pareto最优解为30.5万元。结果表明,遗传算法对非线性优化模型求解效率更高,所得结果节约4万元,验证方法的有效性。
4 结论
1)通过建立高铁突发事件的多级情景要素体系,对高铁突发事件进行特征要素分析,得到相似度最高的源情景作为参考,从而将不确定的资源需求量转化为可预测值。实例验证中情景总相似度最高可达87%,为当前事故情景提供可靠的决策参考。
2)利用“情景-应对”模式预测得到应急资源需求量,确定优化目标并构建调度优化模型,满足高铁应急调度的及时性和经济性。通过改变子目标的权重值适应不同的决策偏好,对高铁应急救援工作有很强的借鉴意义。
3)由于资料收集限制,情景库中源情景较少,导致模型精度不高,下一步研究中需要进一步收集事故情景,丰富情景库数据。

