应用GNSS数据拟合的卫星自主维持星座构型策略

齐彧 李新刚 林骁雄

(中国空间技术研究院通信与导航卫星总体部，北京 100094)

当前，星座已成为航天领域的发展重点。相比于传统大卫星，星座具备冗余度高、成本低廉、实时性好、组网灵活等优点。因此，自2014年开始，大规模星座逐渐成为航天领域的研究热点[1]。近年来，各航天大国纷纷计划打造大规模星座。铱(Irudium)卫星系统公司、美国太空探索技术(SpaceX)公司、一网(Oneweb)公司，均快速推动各自星座的规模化部署进程，低轨星座进入大规模部署阶段。

Irudium卫星系统公司在774.63 km的高度部署75颗新一代铱(Irudium NEXT)卫星，已于2019年实现Irudium NEXT系统的部署[2]。SpaceX公司计划在轨道高度340 km，550 km，1150 km分别部署7518颗、2825颗和1600颗卫星，实现星链(Starlink)星座组网，后期计划在340 km高度轨道进行星座规模扩容，扩容后星座规模将达到42 000颗[3]。Oneweb星座由588颗工作卫星和60颗备份卫星组成，轨道高度1200 km[4]。2019年2月完成首批6颗试验卫星的发射，2020年2月与2020年3月分别发射34颗业务卫星，开始大规模部署[5]。

考虑到未来星座智能化程度越来越高和规模越来越大，自主高精度星座构型维持的需求变得越发突出[6]。星座构型维持策略有双边控制与单边控制2种。其中：双边控制所需的轨道控制既有加速也有减速，单边控制所需的轨道控制仅有加速。文献[7]中基于两行轨道要素数据对典型低轨通信星座的占位保持精度及构型维持策略进行了分析，得到Irudium NEXT和Oneweb星座的站位保持精度为纬度幅角±0.2°，其构型维持策略采用双边控制，且并未实现自主构型维持。文献[8]中对全球星(GlobalStar)系统构型维持策略进行了分析与仿真，结果表明：在单边控制的情况下，GlobalStar系统自主构型维持精度要求为±0.5°，但其在轨维持精度约为±2°。

当前，典型星座的卫星，如Irudium NEXT，Oneweb，Starlink等，一般通过搭载全球导航卫星系统(GNSS)接收机实现星上自主定轨，同时配备电推力器实现轨道控制。对于仅在飞行反方向配置推力器的卫星，采用单边控制能够在不进行姿态调整的情况下实现轨道面内的相位维持，因此广泛用于星座构型维持[9]。然而，随着星座轨道高度的提高，大气阻力的作用逐渐变弱，在考虑GNSS接收机输出参数误差的情况下，容易出现构型维持超差。当前，典型的星载GNSS接收机输出轨道半长轴在动力学滤波后的方差在10米量级。根据这一输出结果进行自主星座构型维持时，轨道高度在1000 km以上时，有可能发生相对纬度幅角超出构型维持精度的情况，进而引起星上自主单边构型维持策略的失效[10]。上述问题产生的主要原因是：星载GNSS接收机得到的直接测量值为轨道瞬根，星上在进行平根计算后再进行动力学滤波，输出的半长轴结果误差过大，导致漂移环变大，进而超过星座构型维持精度要求。因此，如何充分利用星载GNSS接收机提供的轨道测量数据，在基于单边构型维持的情况下，实现卫星高精度自主维持星座构型，成为了星座构型维持任务中急需解决的工程问题。

本文提出一种应用GNSS数据拟合计算的星座构型维持策略，该策略以星载GNSS接收机测量得到的纬度幅角参数作为输入条件，利用相对参考轨道的纬度幅角变化率与相对半长轴之间的对应关系对相对半长轴进行拟合，从而提高星上相对半长轴的确定精度，进而提高单边控制条件下星座构型维持的精度。

1 卫星自主维持星座构型策略

受限于轨道确定精度和轨道控制精度，卫星初始轨道参数与设计参数之间存在初始偏差。同时，运行过程中受到各种环境摄动力影响，导致卫星的轨道参数发生变化。考虑到星座在运行期间需要保持相对构型稳定，防止对地面的覆盖特性发生改变，因此需要进行轨道控制，即要求卫星相对参考轨道的纬度幅角、倾角、升交点赤经维持在给定范围内[11]。

倾角、升交点赤经的维持周期一般较长，可以利用地面规划的手段实现轨道面外的误差控制。卫星通过自主调整相对参考轨道的半长轴，可以改变卫星相对参考轨道的角速度，从而间接控制卫星相对参考轨道的纬度幅角，进而实现星座轨道面内的误差控制。这是卫星自主维持星座构型的核心。由轨道动力学可知，利用大气阻力使轨道半长轴自然衰减这一特性，星座构型维持过程中卫星仅需要提供沿轨道速度方向的推力，因其在构型维持过程中仅采用升轨机动，故称为单边控制策略，考虑到需要利用大气阻力进行降轨，因此单边控制策略多用于轨道高度1500 km以下卫星。文献[12]中对这一控制策略进行了详细的介绍。图1为单边控制策略的漂移环[13]。卫星在相对参考轨道纬度幅角到达控制盒右边界时调整半长轴，使得调整后半长轴高于标称轨道，此时根据轨道特性，卫星相对纬度幅角向左侧漂移；漂移过程中，卫星轨道半长轴受大气阻力作用而逐渐降低，当轨道半长轴低于标称轨道半长轴时，相对纬度幅角向右边界漂移，直至再次达到右边界。重复上述过程，形成图1中所示的漂移环。

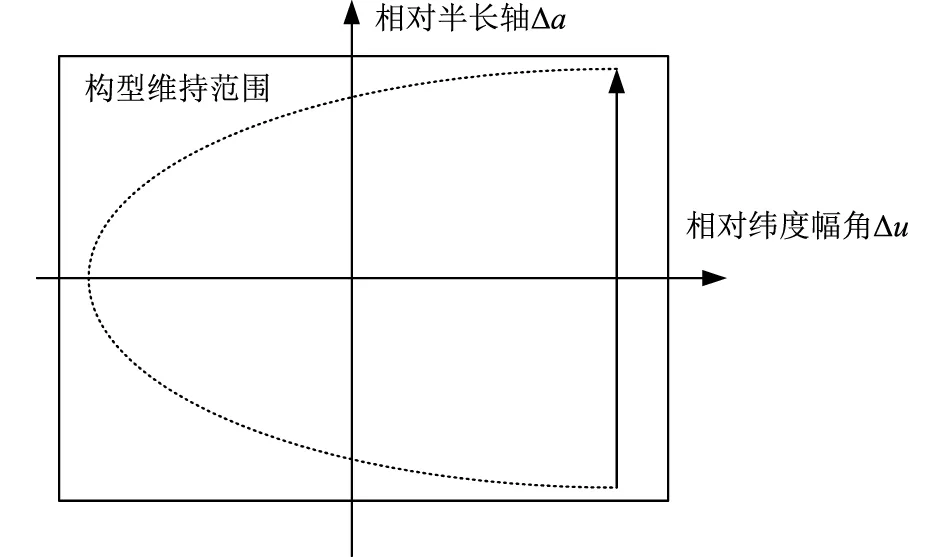
图1 单边控制策略漂移环构型示意

星载GNSS接收机能够直接获取卫星轨道信息，但是其轨道半长轴测量精度往往无法满足自主维持星座构型所需的高精度要求。本文利用卫星半长轴与轨道角速度之间的对应关系，通过相对纬度幅角数据拟合计算得到相对半长轴，从而提高相对半长轴的精度，进而实现卫星自主维持星座构型。星座构型维持策略原理框图如图2所示。

图2中，星座构型维持的参考轨道由地面生成，星上进行轨道计算，得到参考轨道的轨道参数；星载GNSS接收机实时进行自主轨道确定，获得当前轨道根数；卫星利用获取的真实纬度幅角与参考轨道计算得到的纬度幅角计算当前轨道纬度幅角误差，并利用相对半长轴拟合算法自主进行相对半长轴拟合，得到当前卫星相对于参考轨道的半长轴误差及纬度幅角误差；构型维持策略利用半长轴误差及纬度幅角误差计算相对纬度幅角达到调整点的时刻，以及轨道控制所需的半长轴调整量，最后生成构型维持的轨道控制策略，交由星上轨道控制执行机构执行。

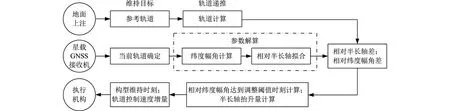
图2 星座构型维持策略原理

利用纬度幅角信息对相对半长轴进行拟合计算，具体实现过程如下。

由轨道动力学可知，对于近圆轨道，纬度幅角变化率与轨道半长轴之间的微分关系如式(1)所示。

(1)

式中：n为轨道角速度；μ为地球引力常数；a为轨道半长轴。

假设参考轨道的半长轴为aR，则卫星相对纬度幅角变化率与相对半长轴之间的对应关系如式(2)所示。

(2)

式中：卫星纬度幅角与参考轨道纬度幅角之差Δu(t)=u(t)-uR(t)；卫星半长轴与参考轨道半长轴之差Δa(t)=a(t)-aR(t)。

对于低轨卫星，轨道半长轴变化主要受大气阻力影响，相对半长轴的变化近似于二次曲线[14]，如式(3)所示。

(3)

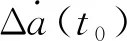
将式(3)代入式(2)，得到式(4)。

(4)

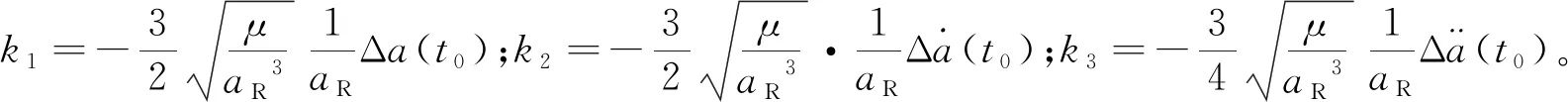
进一步得到相对半长轴变化，如式(5)所示。

Δa(t)=KR[k1+k2(t-t0)+2k3(t-t0)2]

(5)

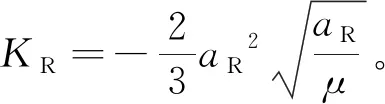
考虑到星上自主处理能力的逐步提高，可以采用更高阶的拟合多项式提升对相对半长轴的拟合精度。采用N阶多项式拟合情况下，卫星相对纬度幅角随时间变化如式(6)所示。

(6)

式中：u(t0)为t0时刻的相对纬度幅角；Ki为计算中所需的多项式拟合系数，i=1，2，3，…。

一般情况下，拟合多项式阶数N越高，拟合的精度越高，但计算复杂度也越高。

利用星载GNSS接收机的轨道参数，结合式(6)可以对相对纬度幅角进行多项式拟合，计算得到参数u(t0)与多项式拟合系数Ki。

将式(6)代入式(2)，得到相对半长轴的拟合公式，如式(7)所示。

(7)

为了提高星座卫星相邻2次构型维持的时间间隔并减少轨道控制次数，通常令漂移环的左边界等于构型维持范围门限值，从而使得漂移时间最长[14]。因此，卫星自主维持星座构型的轨道控制时刻能够利用式(8)求解。

Δu(tf)=ulim

(8)

式中：ulim为构型维持的误差上限；tf为构型维持轨道控制时刻。

在拟合计算结束后，星上能够根据式(8)提前计算轨道控制时刻，并利用式(7)代入构型维持时刻tf，求解得到构型维持时刻的相对半长轴值Δa(tf)。

构型维持的半长轴抬升量使得下一次漂移过程中漂移环达到左边界，因此调整后的相对半长轴如式(9)所示。

(9)

进而得到构型维持中半长轴的抬升量，如式(10)所示。

da(tf)=Δam-Δa(tf)

(10)

式中：Δam为调整后的相对半长轴。

最后，计算得到的构型维持时刻tf与对应的半长轴的轨道机动量da(tf)，作为执行机构轨导控制的输入，最终作为执行机构实施卫星自主维持星座构型轨道控制的输入。

2 仿真与验证

本节以某极轨星座为对象，对应用GNSS数据拟合的卫星自主维持星座构型策略进行仿真，以证明上述策略能够满足高精度的星座构型维持要求。为了便于对比，在仿真结果中同时给出传统的利用GNSS接收机数据，采用动力学滤波作为输入的星座构型维持仿真结果。仿真过程中用到的参数见表1。

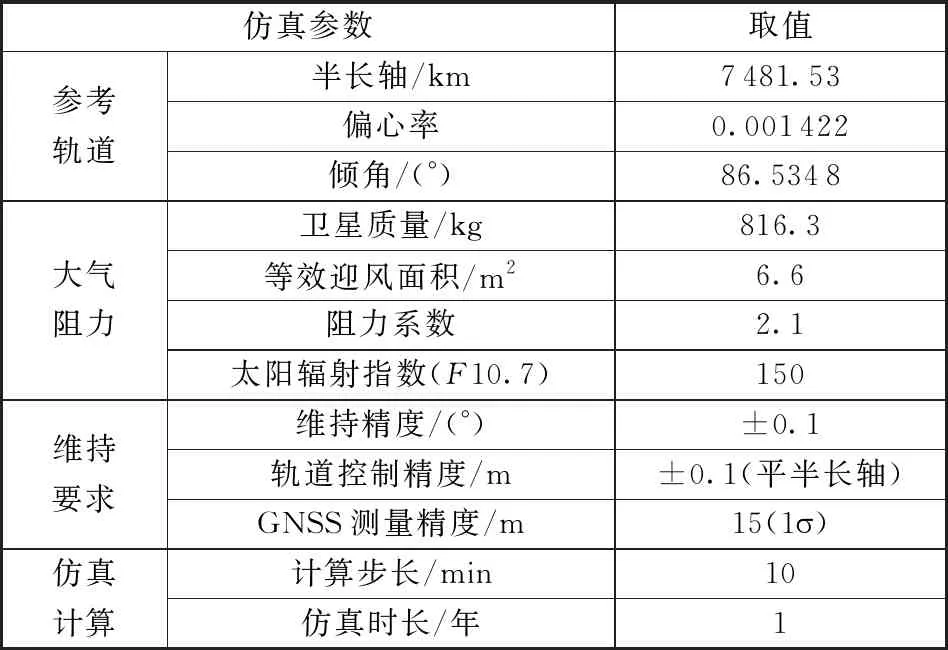
表1 仿真参数

在星载GNSS接收机直接输出的定轨数据中，相对半长轴如图3中点划线所示。从图3中可以看出：星载GNSS接收机直接输出的半长轴数据具有较大的随机噪声，在使用前需要进行动力学滤波，滤波后半长轴的确定误差能够达到10米量级，如图3中实线所示。图3中虚线为地面精密定轨计算得到的相对半长轴理论值。

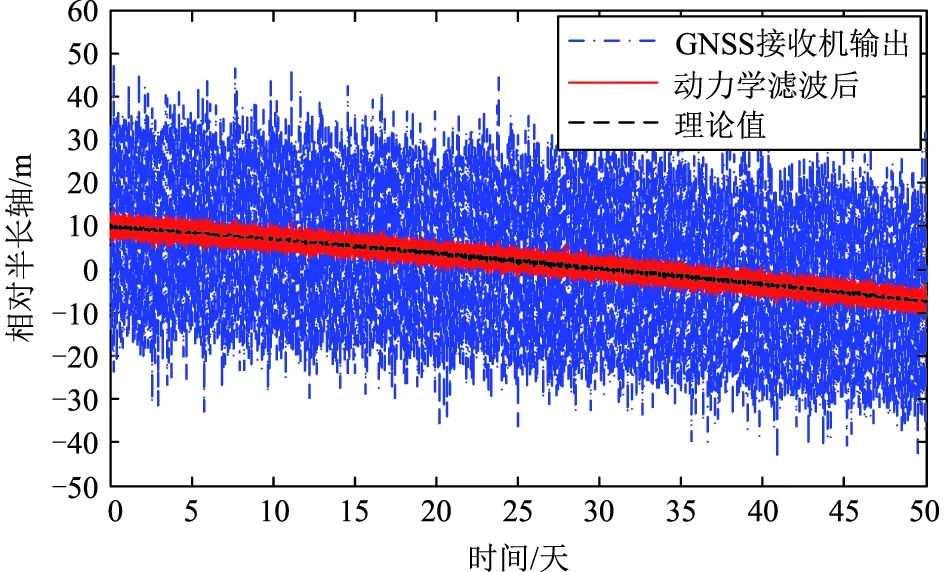
图3 相对半长轴随时间变化(GNSS数据)

星载GNSS接收机输出的相对纬度幅角Δu(t)测量值如图4蓝色虚线所示，可以看到：其同样存在随机噪声。采用式(6)进行二阶拟合，得到拟合后相对纬度幅角Δu(t)变化如图4中红色实线所示，可以看到：拟合后的相对纬度幅角变化与GNSS接收机输出的结果具有一致的变化规律，但是随机噪声明显降低。

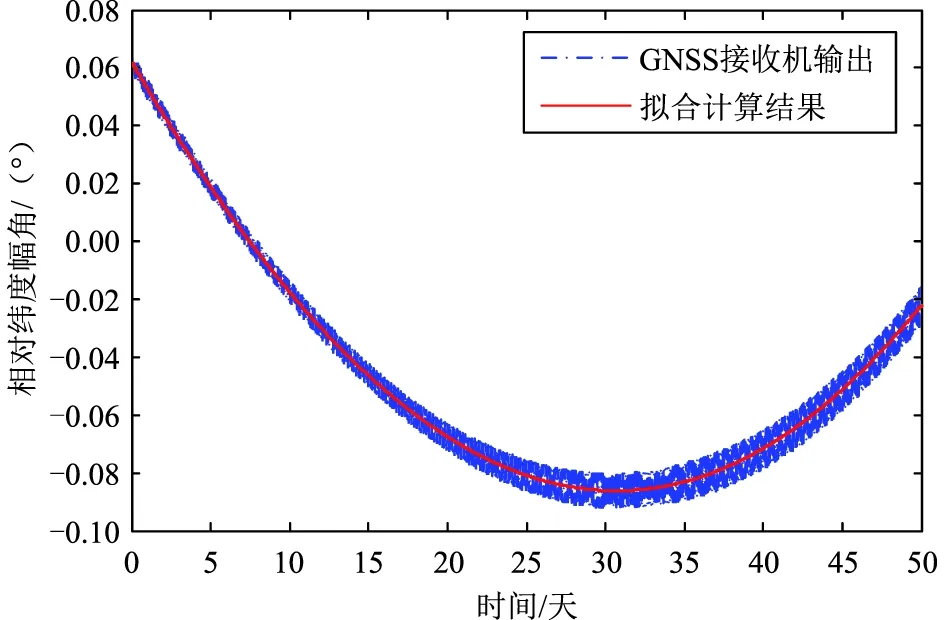
图4 相对纬度幅角随时间变化

进一步利用式(7)进行相对半长轴的拟合，得到相对半长轴计算结果如图5所示。对比图5中拟合计算得到的相对半长轴与精密定轨得到的相对半长轴，可以发现：拟合计算后的相对半长轴变化平稳，波动小；同时，拟合计算后的相对半长轴变化规律与精密定轨得到的相对半长轴变化规律一致，保留了相对半长轴随时间变化的绝大部分信息，能够真实反映轨道参数的变化情况。

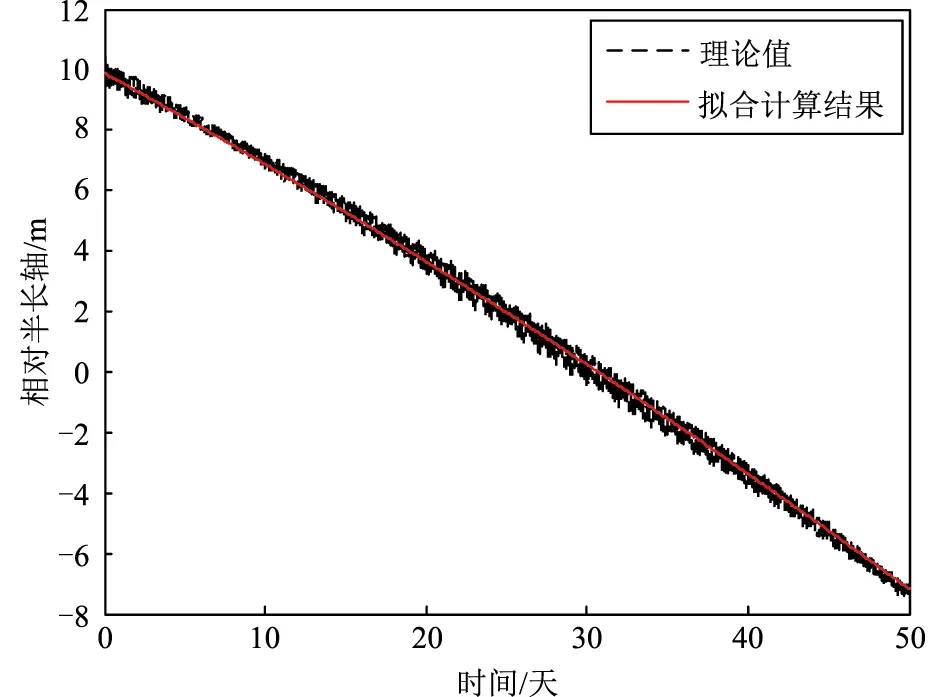
图5 相对半长轴随时间变化(GNSS数据拟合计算)

图6给出了二阶拟合计算得到的相对半长轴与理论值之间的误差变化情况，可以看到：拟合计算得到的相对半长轴误差优于1 m，精度远高于动力学滤波结果。

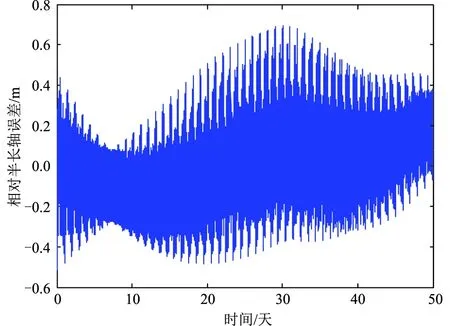
图6 相对半长轴拟合计算误差随时间变化

图7为星座构型维持过程中相对纬度幅角随时间变化结果，可以看到：传统星座构型维持过程中，最大纬度幅角误差达到-0.3°，超出了构型维持精度的要求；而采用本文提出的星座构型维持策略，能够保证构型维持精度优于0.1°。同时，相邻2次构型维持轨道控制间隔约为55天，且具有一定周期性。这种周期性有利于大规模星座构型维持的地面监视工作安排。

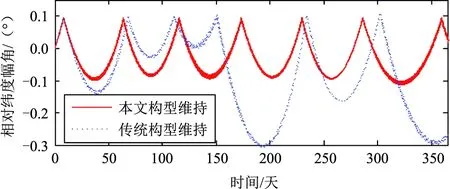
图7 星座构型维持中相对纬度幅角仿真结果

图8给出了星座构型维持过程中漂移环的漂移过程，可以看到：传统星座构型维持策略在每次构型维持后，相对半长轴的分布散差较大，导致漂移环出现漂移量不足与漂移量超出维持精度要求的情况。这种现象的产生，是由于利用动力学滤波算法得到的相对半长轴测量误差散布大。因此，星座构型维持策略计算得到的半长轴调整量与真实所需调整量之间的误差超过了构型维持精度对应漂移环的半长轴上限。在这种情况下，星座构型维持的误差不满足维持要求。相比之下，采用本文星座构型维持策略后，对相对半长轴的拟合计算结果误差更低，满足星座构型维持精度需求。

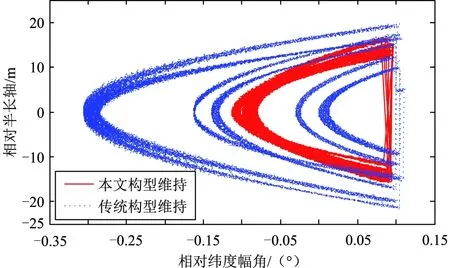
图8 星座构型维持中漂移环仿真结果

与传统星座构型维持策略对比，本文星座构型维持策略主要优势如下。

(1)轨道参数解算部分，通过对纬度幅角的计算与拟合得到相对半长轴，避免了GNSS接收机输出误差较大的半长轴数据直接进入星座构型维持策略计算，从而提高星座构型维持控制器输入参数的精度，使得高精度自主星座构型维持成为可能。

(2)星座构型维持所需的输入参数均来自于星载GNSS接收机对轨道的测量结果，同时对纬度幅角及相对半长轴拟合计算的计算量小，能够实现星上自主运行，无需地面测控系统干预。

(3)星座构型维持策略通过对纬度幅角的拟合得到相对半长轴的变化趋势，拟合算法中多项式阶数可以根据应用需求设计，能够在拟合精度与计算量之间得到平衡。

3 结束语

本文提出了应用GNSS数据拟合的卫星自主维持星座构型策略。相比于传统星座构型维持策略，所建立的新策略采用星载GNSS接收机输出的纬度幅角信息作为维持策略的输入条件，利用相对纬度幅角变化率与相对半长轴之间的对应关系进行相对半长轴的多项式拟合计算，得到精度更高的相对半长轴拟合结果，进而提高星座构型维持的精度。仿真结果表明：采用应用GNSS数据二阶拟合计算得到的相对半长轴误差小于1 m，优于采用动力学滤波得到的结果；星座构型维持精度能够提高1倍以上，满足未来大规模星座构型自主高精度维持的需求。同时，在星座构型维持过程中，相邻2次构型维持之间的时间间隔近似相等，具有一定的周期性，有利于卫星自主维持星座构型期间地面监视工作的安排。