一种异轨等高MEO卫星的建链模式设计方法
刘飞 宋效正 杨立峰 张凌燕
(上海卫星工程研究所,上海 201109)
随着遥感技术的不断发展,空间设施的应用越来越重视星间、星座间的协同探测与感知,用于发挥并提升空间设施的体系效能。美国天基红外系统-低地球轨道(SBIRS-LEO)卫星系统通过星间链路组成一个星际互联网,借助该星间链路实现彼此间通信和监测信息的传递,完成对目标的全球实时覆盖[1-2]。因此,推进各类卫星建链融合成为航天技术发展的必然趋势。
星间链路可以分为同轨星间链路和异轨星间链路[3]。理论上,同轨卫星除相位不一致外,其他轨道参数均相同,因而相互间指向固定。异轨卫星相对运动复杂,卫星的相对位置和姿态始终处于动态变化中[4]。现有四大全球卫星导航系统均采用Walker卫星星座[5-7]开展异轨星间体系建链,各轨道面升交点漂移速率相同,轨道面间存在多条永久链路,确保了稳定的链路结构,但不适用于轨道面升交点漂移速率不相同的工况。同时,卫星分布需要依据特定条件[8],链路指向范围取决于轨道特性,存在天线转动范围过大与星上其他设备干涉的问题[9]。
本文提出一种半长轴相等的0°倾角MEO卫星与倾斜MEO卫星建链模式,该模式允许拟建链轨道面的升交点漂移速率不相同、异轨卫星间无需永久可见,并通过链路动态切换确保固定数量的稳定、连续链路,且链路指向范围最小。
1 建链模式概述
假设圆轨道1和圆轨道2上分别均布i和j颗卫星(i,j为2,3,4,…),两轨道上卫星运行方向一致,即两轨道面负法线方向的夹角小于90°。如图1所示,O为地心,以两轨道交线为X轴、圆轨道1轨道法线为Z轴构建参考坐标系,Y轴符合右手法则,+X轴指向卫星Bj相对圆轨道1升起的方向,+Z轴指向与圆轨1的轨道负法线方向(-YA)一致。卫星在轨道上的位置以相位Δu表示,从+X轴绕轨道负法线度量为正,Δu∈[0,2π]。
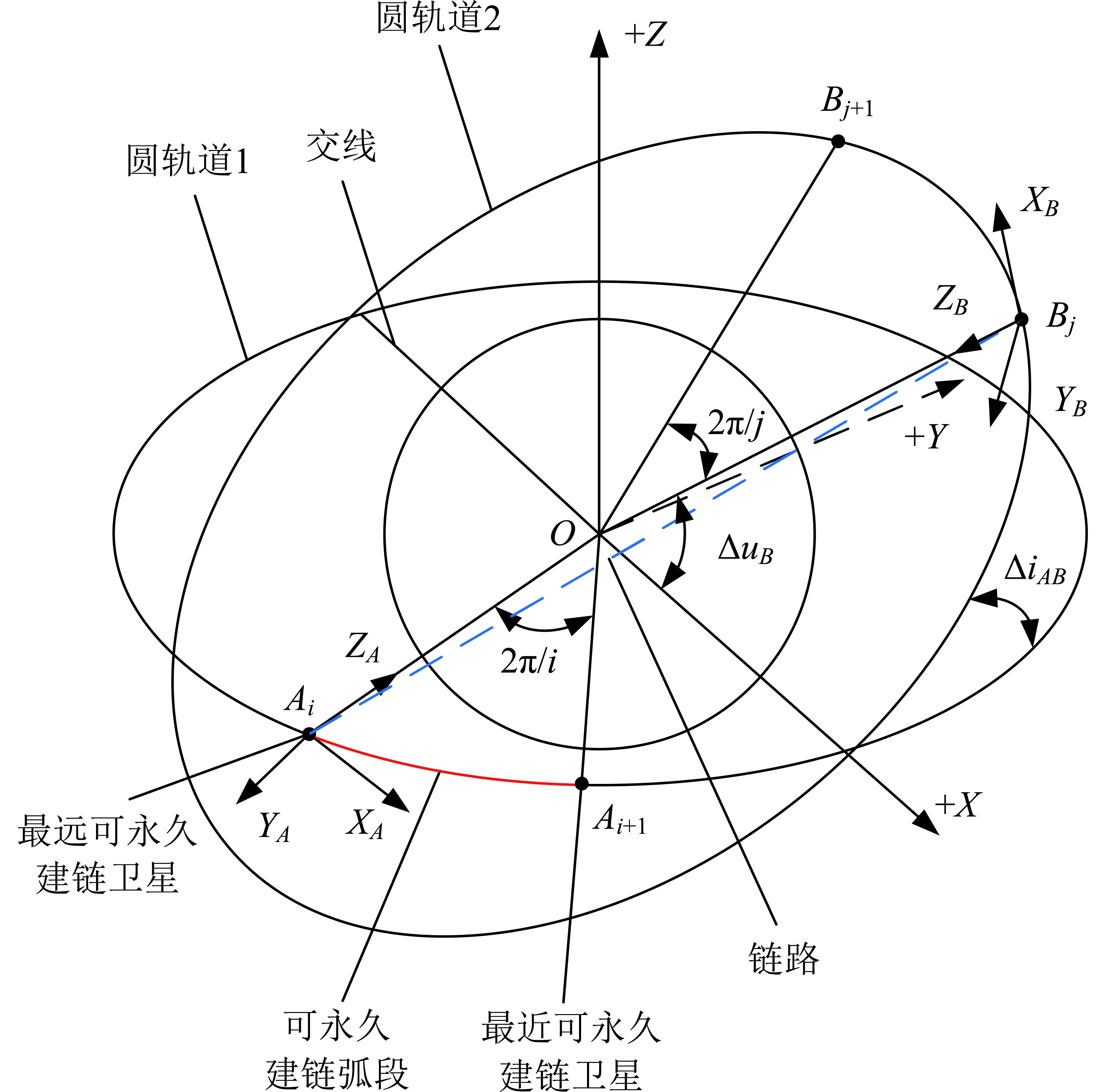
图1 建链示意
地球摄动会引起轨道漂移[10],造成两轨道面相对、持续漂移,异轨星间的相对位置将大范围动态变化,链路指向范围将超出天线能力,链路无法长期保持。假设圆轨道2绕-Z轴漂移(若绕+Z轴漂移,则将坐标系XYZ建立在圆轨道2上),漂移后两轨道在参考坐标系中位置如图2(a)所示。根据参考坐标系定义,将+X轴重新建立在交线上,则轨道漂移效果相当于圆轨道1上卫星绕+Z轴转动。假设卫星Bj与卫星Ai在建链若干个轨道周期后,由于轨道漂移影响,Ai绕+Z轴转动到了Ai+1,如图2(b)所示。为使卫星Bj的天线指向范围不随卫星Ai的“相对转动”进一步扩大,此时,Bj需要将链路从Ai切换到Ai-1,从而消除轨道漂移带来的影响,将链路指向范围控制在天线能力范畴内。
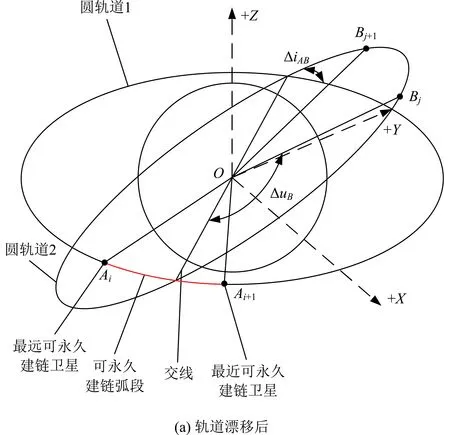
图2 链路切换示意
为详细论述建链模式并支撑前述假设,本文从单颗卫星可见性与轨道特性入手,找到天线指向范围与目标轨道上可永久见弧段的关系,进而提出与建链模式相匹配的天线指向范围计算解析式及建链模式实现流程。
2 可见性及轨道特性分析
2.1 可见性分析
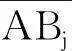
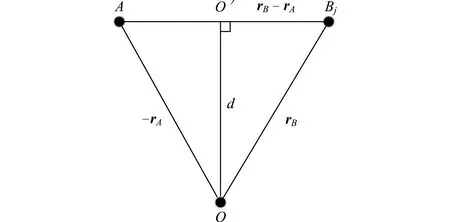
图3 地心到2颗卫星连线的距离
由几何关系可知
(1)
2颗卫星可见的首要条件是地心到它们连线的距离大于地球半径加上大气强电离层高度[11],即:当d≥Re+h时,卫星A和Bj可见;反之,不可见。其中:Re为地球半径;h为强电离层高度。
当卫星A为Bj最远可见时,d=Re+h,令a为轨道半长轴,有
(2)
如图4所示,令卫星Bj在圆轨道1上的投影为B′,位置用ΔuB′表示,卫星A的位置矢量表示为[0 -a0]T,卫星B的位置矢量表示为a·[cos(ΔuB) sin(ΔuB)cos(ΔiAB) sin(ΔuB)sin(ΔiAB)]T,圆轨道1负法线向量n1可表示为[0 0 1]T。因而,卫星B投影B′的位置矢量rB′=(n1×rB)×n1。 将rA和rB点积,并代入到rA和rB′点积后的式子中,化简可得

图4 可见区域分析示意
cos(∠AOB′)=
(3)
定义∠AOB′对应的弧段为卫星B在圆轨道1上的可见弧段,从式(3)可看出,卫星B对圆轨道1上的可见弧段随轨道运动动态变化。
2.2 轨道特性
由图4中ΔOBjC,ΔOB′C,ΔOBjB′的几何关系,可求得卫星Bj的相位角ΔuB与其投影ΔuB′的关系为
ΔuB′=arctan(tan(ΔuB)cos(ΔiAB))
(4)
假设当ΔuB为0时,卫星Ai处于点Ai′,卫星Ai和Bj在圆轨道1上的相位差为Δufar_1,由于2颗卫星半长轴相等,飞行速率也相同,由几何关系可知
∠AiOB′=Δufar_1-ΔuB+ΔuB′
(5)
为使Ai成为卫星Bj在-XB轴方向的最远可永久见的卫星,在飞行过程中,卫星Bj的(-XB轴方向)可见弧段对应的地心夹角(∠AOB′)始终要不小于其投影点与Ai的相位差(∠AiOB′),结合式(5)可得
(6)
需要注意的是,上述可见性及轨道特性分析虽然是在两轨道相对位置不变的情况下得出的,但轨道漂移只影响交线的位置,而参考坐标系X轴建立在交线上,随交线一起变动,因而分析结果不受影响。
3 指向分析及建链流程
3.1 天线指向分析
3.1.1 天线指向定义
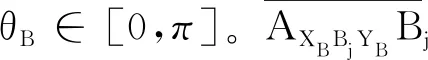
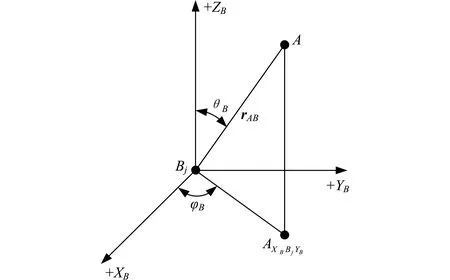
图5 天线指向定义
θA,φA的定义类似,不再赘述。
3.1.2 天线离轴角分析
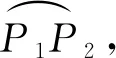
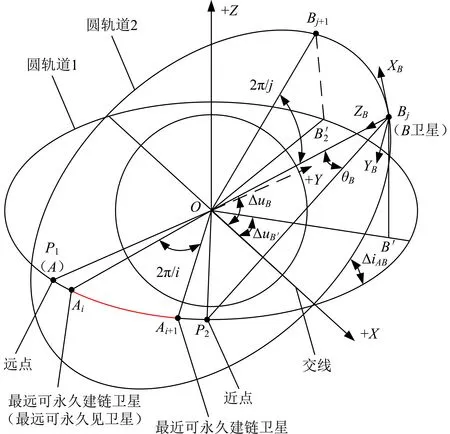
图6 可永久建链弧段分析
为使Ai+1成为Bj在-XB轴方向最近可永久建链的卫星,卫星Bj的-XB轴方向盲区(∠P2OB′)要始终不大于其投影与Ai+1的相位差(∠Ai+1OB′),假设当ΔuB为0时,卫星Ai+1与Bj在圆轨道1上的相位差为Δunear_1,因Ai和Ai+1相差2π/i,有Δunear_1=Δufar_1-2π/i,结合式(5)和式(7),可得式(8)。
(7)
(8)
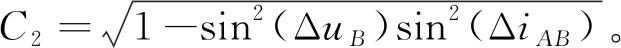
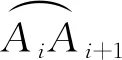
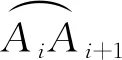
3.1.3 天线方位角分析
需要注意的是,建链过程中若卫星Ai+1一直在Bj的-XB轴方向飞行,那么Bj只需要用到天线指向范围的-XB轴方向半圆锥,此时有
Δufar(min)_1-2π/i-ΔuB+ΔuB′≥0
(9)
将式(9)对ΔuB求导,并找到(ΔuB-ΔuB′)的最大值,求得
Δufar(min)_1≥2π/i+
(10)
若Ai+1在飞行过程中自-XB轴方向穿越Bj出现在+XB轴一侧,那么Bj还需要用到天线指向范围的+XB轴半圆锥。考虑Bj正好从圆轨道1升起或下降时,参考图3可知,当Ai+1无限接近Bj时,∠Ai+1OBj等于0,此时,2颗卫星离轴角为90°,它们有最大指向范围为+Z轴方向半球。
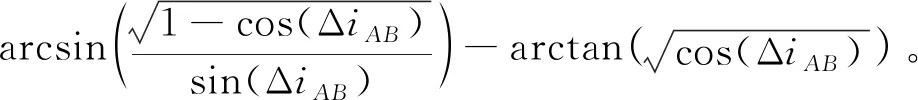
3.2 建链策略及流程
如图2(b)所示,轨道漂移的效果相当于Ai绕+Z轴转动到了Ai+1,若两轨道上卫星相位差相等,那么Ai恰好为卫星Bj+1最远可永久建链的卫星,当Bj将链路从Ai切换到Ai-1时,Bj+1也可将链路从Ai-1切换到Ai,从而实现链路无缝接替。若圆轨道2上卫星相位差更大,那么Ai将超出Bj+1最远可永久建链卫星的范围;当2π/j∈(2π/i,4π/i)时,Ai+1也不是Bj+1最近可永久建链卫星,Ai+1与Bj+1可永久建链,但Ai处于待建链状态;当2π/j=4π/i时,Ai+1是Bj+1最远可永久建链卫星,Bj+1可将链路从Ai+2切换到Ai+1,链路同样可无缝接替,只是Ai处于待建链状态。依次类推,可知:①当2π/j=2nπ/i(n=1,2,3,…)时,两轨道上卫星具有同时切换链路的特点,链路数为(i/n)。②当2π/j≠2nπ/i时,两轨道上卫星链路只能逐条切换,链路数为j。
3.2.1 两轨道均布卫星数相等
由第3.1节分析及建链策略可知,两轨道上卫星的单向最远可永久见弧段与最小离轴角值相等、链路数N与各轨道上卫星数量相等,即
(11)
两轨道上卫星具有同时切换链路或保持稳定建链状态的特点,建链流程如图7所示。
图7 两轨道上均布卫星数相等时的建链流程
3.2.2 两轨道均布卫星数不等
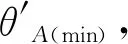
(12)
当i 两轨道上卫星具有逐条切换链路的特点,每颗卫星都要实时计算拟建链卫星在参考坐标系下的位置,建链流程见图8。 图8 两轨道上均布卫星数不等时的建链流程 如表1所示,选取4个工况对本文建链模式设计方法进行验证,结果见表2。其中:半长轴a取2500 km,升交点Ω取0,强电离层高度h取200 km。此外,由式(11)和式(12)可知,两轨道上卫星的单向最远可永久见弧段和天线离轴角相等,下文表述时不再作区分,分别以Δufar(min)和θmin表示。 表1 典型工况的链路分析和天线指向范围 工况1中,可永久见弧段对应地心夹角(2Δufar(min))小于相邻卫星相位差,两轨道间没有稳定链路,由图9(a)可知,即使将天线指向范围调整到最大,两轨道间链路也是时有时无。 工况2中,2Δufar(min)大于相邻卫星相位差,两轨道上均布卫星数均为3,因而有3条稳定链路。但单向可永久见弧段对应的地心夹角(Δufar(min))小于指向范围类型判断阈值ufield,由第3.1节分析可知,其指向为+Z轴方向半球,且最小离轴角θmin为90°。由图9(b)可看出:当指向范围为半圆锥(1/4球)、θmin为90°时,两轨道间链路时有时无。当指向范围改为半球时,两轨道间链路为3条或6条,如图9(c)所示,6条链路表示每颗卫星均对目标轨道上的2颗卫星可见,此时为链路切换期,实际链路只有3条。当离轴角稍微减小时,如图9(d)所示,链路有时只有2条,不能保持3条稳定链路,验证了天线指向分析的正确性。 工况3中,Δufar(min)大于ufield,卫星指向范围应为半圆锥。从图9(e)可看出:当圆轨道1上卫星A天线指向范围为+X轴方向半圆锥、圆轨道2上卫星B天线指向范围为-X轴方向半圆锥时,两轨道间有7条稳定链路,链路切换可用时间为3 min,这意味着每颗卫星同时对目标轨道上2颗卫星可见的时间很短。结合式(7)离轴角越(大)小、可看到的目标轨道弧段越(大)小的结论可知:此时的离轴角为临界值,也即最小值,进一步验证指向范围分析的正确性。需要注意的是,由于STK软件中地球模型更精确,以缩小链路切换可用时间为目标修正后的离轴角也更精确,如表2中工况3所示,离轴角计算值与STK软件修正值有偏差,但很小。 表2 典型工况的离轴角计算结果与STK软件仿真值比较 工况4中,Δufar(min)大于ufield,且两轨道上均布卫星数量不等,根据式(12)可知,圆轨道1上卫星最小离轴角取圆轨道2上卫星最小离轴角θB(min),且两轨道上卫星天线指向范围均为半圆锥。从图9(f)可看出:当圆轨道1上卫星A天线指向范围为+X轴方向半圆锥、圆轨道2上卫星B天线指向范围为-X轴方向半圆锥时,两轨道间有5条稳定链路,且最多时有6条链路。这意味着同一时段内只有1颗卫星能同时看到目标轨道上的2颗卫星,也即链路切换只能逐条进行,验证了建链流程的正确性。 图9 典型工况的链路仿真(STK) 上述4个工况的建链仿真结果表明:本文建链模式具有稳定链路数量固定、天线指向范围最小的特点,且链路切换与本文提出的建链流程完全一致,具有可行性。 本文针对异轨建链指向范围大的问题,在分析单颗卫星建链指向范围和轨道运动特性的基础上,研究了异轨等高MEO卫星的建链模式,推导出了最小离轴角解析式和指向范围判断式,并结合不同类型建链情况提出了两类建链模式及匹配的最小离轴角解析式。经对典型工况的稳定链路数、指向范围类型及最小离轴角进行计算,并与STK软件仿真修正结果比对,结果表明:本文提出的异轨等高MEO卫星建链模式设计方法完全可行,最小离轴角计算值与仿真值偏差小于0.1°,优于工程要求的指向精度(0.2°),具备工程应用价值。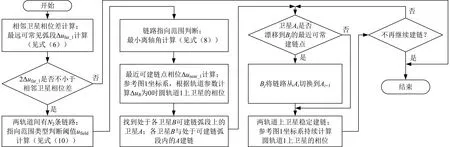
4 仿真验证
5 结束语

