空间宏微机械臂振动抑制最优轨迹规划
尹旺 王翔
(北京空间飞行器总体设计部,北京 100094)
随着空间机械臂在航天领域的广泛应用,复杂多样的空间任务对机械臂的综合性能提出了更高的需求,如快速响应、高精度、小自重和大工作范围等[1]。因此一些国家试图在大机械臂的末端再附加一个小的机械臂,大的机械臂称为宏机械臂,小机械臂称为微机械臂,研究表明这种宏微结构能大大改善机械臂的性能。加拿大的空间站遥操作机械臂系统(SSRMS)与其末端的专用灵巧机械臂(SPDM)、日本的实验舱遥控机械臂系统(JEMRMS)以及中国天宫空间站上的核心舱机械臂(CMM)和实验舱机械臂(EMM)均采取了宏微机械臂的设计[2]。
为了减轻自重,节约发射成本,宏机械臂的臂杆通常采用低密度的碳纤维材质,这种大跨度、轻质的宏机械臂通常会表现出一定的柔性特性。中国空间站上的宏微机械臂采用的是分时独立控制的方式,即先由宏机械臂完成大范围的转移—将微机械臂带到期望的工作区域,然后由微机械臂执行细微操作,此时的宏机械臂相当于为微机械臂提供一个平台[3],由于两者之间存在动力学耦合,因此微机械臂的运动会激起柔性基座的弹性振动,而基座的弹性振动反过来又会影响微机械臂末端的操作精度。文献[2]指出载荷照料是实验舱机械臂的主要任务之一,而机械臂末端的高精度定位是完成载荷出舱、安装、拆卸和回收的首要前提,因此减小机械臂在运动过程中产生的振动是工程中需要解决的难题。
文献[4]设计了一种被动三自由度变刚度的基座用来模拟柔性宏机械臂,该柔性基座能模拟宏机械臂在各种不同构型下的刚度特性。文献[5]中基于阻抗控制算法为宏机械臂设计了相应的微机械臂,试验表明该宏微机械臂系统能完成柔顺运动。文献[6]中为JEMRMS系统设计了自适应控制器,在系统模型存在不确定性的情况下仍能对宏机械臂的弹性振动进行有效抑制。文献[7]针对冗余自由度机械臂安装在柔性基座的模型,应用奇异摄动方法对柔性基座的弹性振动进行了抑制,并通过试验验证了算法的有效性。文献[8]同样采用奇异摄动方法对空间机械臂的弹性基座进行了抑振,算法的实质是将机械臂动力学模型从时间尺度上分解为快、慢两个子系统,并分别进行控制。文献[9]针对柔性基座机械臂提出一种基于反作用零空间的复合控制方法,使机械臂在运动过程中几乎不对柔性基座产生扰动。考虑到基座在重力作用下发生弹性位移,文献[10]为柔性基座机械臂设计了一种柔顺控制律,在不需要基座运动信息的情况下仍能补偿末端执行器的静态偏差。
以上研究从主动控制算法层面提出了柔性基座弹性振动,一方面控制算法较为复杂,有待进一步在轨验证,另一方面振动抑制效果受限于机械臂构型及运动轨迹。本文以基座弹性振动为优化目标进行轨迹规划抑振的研究,基座的振动得到抑制之后机械臂末端的定位精度会相应提高。
1 系统动力学方程
不失一般性,以作平面运动的三连杆柔性基座机械臂为例,建立柔性基座机械臂的动力学模型,系统结构如图1所示。其中:微机械臂的基座(M)通过弹簧和阻尼器与惯性空间连接,弹性系数和阻尼系数用k和c表示。为表示机械臂各连杆之间的相对位置关系,建立各连杆的固连坐标系oixiyizi(i=1,2,3),坐标系{i}的原点位于第i个连杆的关节处,连杆xi沿着臂杆指向下一关节,zi垂直纸面向外,通过右手螺旋定则确立yi,连杆的相对转角θi定义为xi-1绕zi到xi旋转的角度。图1中:oMxMyMzM为柔性基座M的固连坐标系,omxmymzm为机械臂末端坐标系,o0x0y0z0为惯性坐标系,基座相对于基坐标系的弹性位移记为δ。
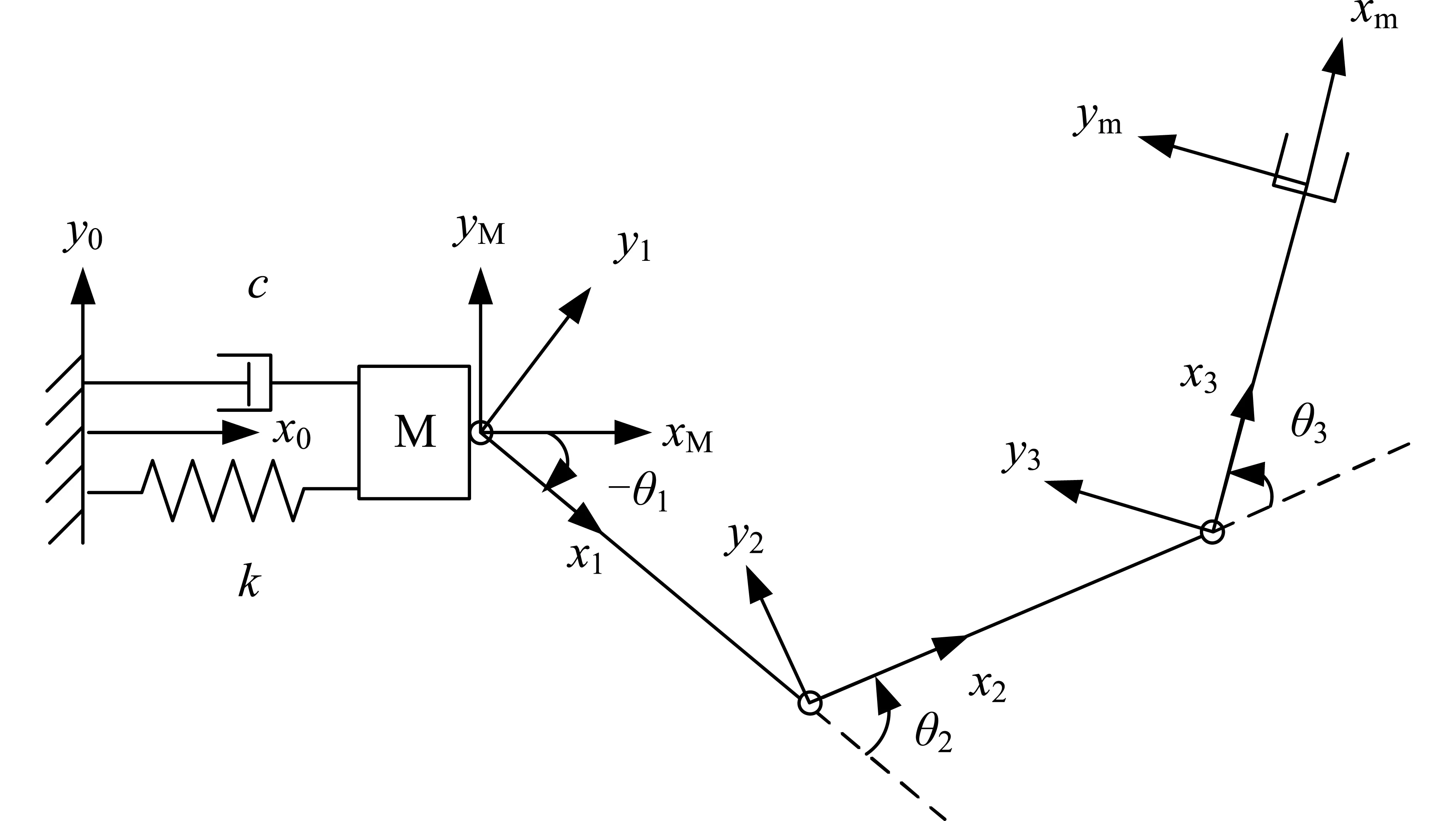
图1 柔性基座机械臂系统
为简化模型,作出以下假定:①弹簧只在水平方向作伸缩运动;②不计弹簧的分布质量;③微机械臂各连杆为均质刚性杆,连杆i长度为li;④动力学模型中不考虑重力影响。
1.1 机械臂运动学
微机械臂连杆i的质心在惯性系下位置矢量可表示为
(1)

(2)

连杆i的角速度可表示为
(3)

1.2 柔性基座机械臂动力学

(4)
式中:mi和Ii分别为连杆i的质量和转动惯量,M为基座质量,等式右边第1项为微机械臂的平动动能,第2项为微机械臂的转动动能,第3项为柔性基座的动能。
由于不计重力作用,因此系统中的势能仅为线性弹簧伸缩存储的弹性势能
(5)
式中:δ为基座振动位移。
另外,系统中阻尼器产生的耗散能可表示为
(6)
将式(4)~(6)求得到的动能、势能以及耗散能代入到第二类拉格朗日方程得到柔性基座机械臂的动力学方程为
(7)
式中:Hb∈R1为柔性基座的质量特性;Hbm∈R1×3为柔性基座和微机械臂之间的惯性耦合矩阵;Hm∈R3×3为微机械臂的惯性矩阵;cb∈R1和cm∈R3×1为非线性项;τ∈R3×1为微机械臂的关节驱动力矩矢量。
由式(7)的上半部分得到柔性基座在平衡位置附近的弹性振动方程为
(8)
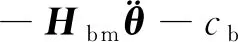
(9)
式中:s1=sinθ1;c1=cosθ1;s12=sin(θ1+θ2);c12=cos(θ1+θ2);s123=sin(θ1+θ2+θ3),c123=cos(θ1+θ2+θ3)。
2 关节空间的轨迹规划
关节空间的轨迹规划是指机械臂只需要完成空间点到点的运动,对末端的运动轨迹没有要求。规划流程是首先获得参数化的关节轨迹,以参数化的变量为个体,以目标函数作为评价函数,最后采用优化算法对优化参数进行调整。本文采用四级龙格-库塔法对式(8)所示的基座振动方程进行数值求解,即可求得基座振动位移δ的时间历程,并以基座最大振动幅值作为目标函数。
2.1 参数化关节轨迹模型
为了使机械臂关节的运动轨迹更加光滑同时不至于使轨迹方程过于复杂,本文用分段函数描述关节的运动轨迹,该分段函数分别为4次、3次、4次的多项式,本文简称为“4-3-4”形式的运动轨迹,分段函数的表示达式为
(10)
式中:a0,a1…a4,b0、b1…b3,c0,c1…c4为分段多项式的待定系数,关节轨迹曲线的大致形状如图2所示。假设各关节的运动轨迹满足初始及终止时刻速度和加速度为零,同时分段轨迹函数的连接处速度和加速度连续,在该条件约束下能唯一确定各关节的运动轨迹。

图2 “4-3-4”参数化轨迹曲线
现将该轨迹函数参数化,引入如下的设计参数,也是后续的优化变量。已知机械臂运动的总时长tf以及各关节的起始角度θj0和终止角度θjf(j=1,2,3),引入一组待定参数γj和βj,γj和βj的取值均在0和1之间,为了方便表示,将所有待定参数组合在一起,表示成λ=[γ1γ2γ3β1β2β3],当优化参数λ给定后,3个关节的运动轨迹唯一确定,因此关节的轨迹规划问题转化成待定参数的优化问题。
(11)
式中:γj=(tj2-tj1)/tf;βj=(θj2-θj1)/(θjf-θj0)。
2.2 基于遗传算法的优化分析
2.2.1 仿真条件
由于遗传算法是一种简单、高效的全局优化算法,仅仅以目标函数作为搜索信息就能得到最优解,因此本文选用遗传算法,以微机械臂运动过程及运动结束后基座的振动幅值为优化目标,通过对关节的轨迹参数λ进行优化实现抑振目的。该优化模型的数学表达式为
(12)

2.2.2 仿真结果分析


图3 目标函数的变化曲线
优化后的待定参数代入式(10)和(11),即可得到关节1、关节2和关节3的角位移函数,如图4所示,从图中可见各关节的转动轨迹光滑连续,在始末时刻的速度和加速度为0,工程上易于实现。

图4 关节的角位移曲线
当微机械臂各关节的运动规律已知时,根据式(8)可求得柔性基座的弹性位移,如图5所示。从仿真结果可以发现,微机械臂基于对照参数组以及5次多项式的轨迹进行运动,激起的基座振幅达到0.156 m和0.073 m,相比之下,按照优化后的关节轨迹进行运动振动幅值仅为0.039 m,表明文中的轨迹规划方法能有效抑制柔性基座的弹性振动。图6给出了微机械臂按照不同路径进行点到点的运动时对基座的等效激振力,显然,对照组的等效激振力幅值最大,五次多项式的幅值次之,基于优化轨迹运动产生的激振力幅值最低,这与图5中基座的振动情况相一致。

图5 柔性基座的振动位移曲线

图6 微机械臂运动产生的激振力
3 冗余机械臂自运动优化
由于冗余自由度微机械臂具有“自运动”能力,使其具有很强的灵活性,因此在抑制基座的弹性振动方面也有很大优势。当机械臂末端需要跟踪特殊轨迹时,可以对机械臂逆运动学中的自运动项进行优化,在保证末端跟踪轨迹的同时,最小化基座振动。
机械臂末端广义速度与关节角速度之间的关系为

(13)
式中:J(θ)为机械臂的雅克比矩阵,随着机械臂关节角的变化而变化。由矩阵理论知,式(13)的逆解为
(14)
式中:J+=JT(JJT)-1称为雅克比矩阵的伪逆;h为优化系数,为保证关节的连续顺滑,令h按照机械臂末端的速度曲线进行变化,即为四次多项式函数。等式右边第1项是最小范数解;第2项是冗余自由度机械臂的自运动项,指机械臂关节在零空间内产生自运动但不会引起末端的运动,机械臂在零空间的速度项只会引起机械臂构型的变化而末端的状态不受影响。因此本部分以自运动项作为优化项对机械臂运动过程中产生的基座反作用进行优化。
3.1 仿真条件

(15)

3.2 仿真结果分析


图7 自运动优化前后的基座振动曲线
由图8可知最小范数解的物理含义是机械臂各关节以最小的运动量完成末端轨迹跟踪,图9表明当冗余机械臂中自运动项不为零时会增加各关节的运动量,尽管在运动时间相同的情况下,后者引起的基座振动幅值仍小于前者,实质上是通过选择合适的“自运动”使微机械臂产生较小的激振力,于是柔性基座受迫振动的幅值也较小,图10为微机械臂的刚性运动对柔性基座产生的等效激振力。
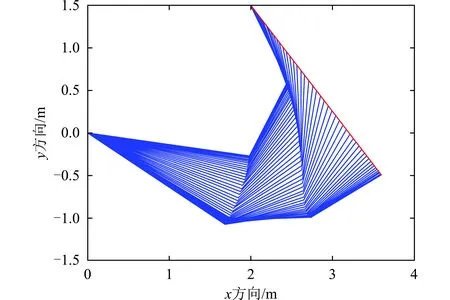
图8 基于最小范数解的运动轨迹

图9 最优自运动的运动轨迹

图10 微机械臂运动产生的激振力
虽然基于自运动项对机械臂的某项指标进行优化时是以牺牲关节的运动量为代价的,尽管如此,基于自运动的优化方法在工程中仍有一定应用价值,因为机械臂运动所消耗的电能在太空中来源于可再生能源。相比于关节运动所消耗的电能,减小宏机械臂弹性振动,提高组合臂末端的操作精度有更大意义。
4 结束语
本文从轨迹优化层面,采用了两种方法对宏微机械臂振动抑制问题进行了研究。首先针对“4-3-4”形式的关节轨迹函数设计了振动抑制目标优化函数,对微机械臂进行了轨迹规划;然后将遗传算法与冗余自由度机械臂的逆运动学理论相结合,对逆运动学中的自运动项进行优化。仿真表明两种方法都能对柔性基座的振动抑制起到良好的效果。需要指出的是,文中所建立的柔性基座机械臂动力学模型是简化后的理想模型,对于我国空间站上搭载的大、小组合机械臂系统,大臂末端可以等效成具有六自由度弹性振动的柔性基座,小机械臂具有七自由度,其动力学方程极其复杂,本文从原理上提出并验证了利用运动轨迹优化进行振动抑制方法的有效性,后续可进一步针对复杂机械臂动力学模型验证本文方法的有效性。

