改进自适应蚁群的城市道路智能车路径优化

裴文鑫 孙宁 马健霄

摘 要：为优化城市道路中智能车辆规划路径的长度与转折次数，本文提出一种改进的自适应蚁群算法。以栅格法对城市道路环境网格化处理，以路径最短、转折次数最少为优化目标函数，改进邻域搜索范围，将8邻域扩大为24邻域，利用启发函数更新初始信息素，动态调整信息素挥发系数，并提出返回上一步的死锁策略，最后考虑曲率限制，以三次B样条曲线法（B-spline curve）平滑优化处理。此研究表明，在随机生成的城市环境地图模型下，该算法较标准蚁群算法与自适应算法，路径长度分别缩短3.89%、8.38%，路径节点分别减少28%、24.2%，收敛次数分别减少37.5%、20%。此研究结果为城市道路智能车辆路径优化提供较好的理论依据。

关键词：智能车辆;城市道路;自适应蚁群算法;邻域搜索;B条曲线法;路径优化

中图分类号：U463;TP18;S77    文献标识码：A   文章编号：1006-8023（2022）01-0152-07

Improved Adaptive Ant Colony-based Urban Road Smart

Car Path Optimization

PEI Wenxin， SUN Ning*， MA Jianxiao

（College of Automobile and Traffic Engineering， Nanjing Forestry University， Nanjing 210037， China）

Abstract：In order to optimize the length and number of turns of intelligent vehicle planning paths in urban roads， this paper proposes an improved adaptive ant colony algorithm. The raster method is used to grid the urban road environment， the shortest path and the least number of turns are used as the optimization objective function， the neighborhood search range is improved， the 8 neighborhood is expanded to 24 neighborhoods， the initial pheromone is updated using a heuristic function， the pheromone volatility coefficient is dynamically adjusted， and a deadlock strategy of returning to the previous step is proposed， and finally the curvature limitation is considered and the three-time B-spline curve method is used to process smoothing optimization. This study shows that the algorithm reduces the path length by 3.89% and 8.38%， the path nodes by 28% and 24.2%， and the number of convergence by 37.5% and 20%， respectively， compared with the standard ACO and the adaptive algorithm under the randomly generated urban environment map model. The results of this study provide a good theoretical basis for the optimization of intelligent vehicle paths on urban roads.

Keywords：Smart vehicle; city road; adaptive ant colony algorithm; neighborhood search; B-spline curve;  path optimization

0 引言

城市道路下智能車辆的路径规划算法是当前无人驾驶领域的研究热点，而算法的优劣将直接影响着车辆的通行能力[1-3]。以迪杰斯特拉（Dijkstra）算法[4-5]、A*（A-Star）算法[6]为代表的传统路径算法，搜索效率低、易陷入局部最优，很难应用于空间复杂度较高的城市道路[7]，且受邻域搜索限制、求解路径的节点及转折数较多。

目前国内外学者对模拟退火算法[8]、遗传算法[9]、粒子群算法[10-11]等为代表的智能仿生算法方面做了大量研究，该类算法通过模仿生物行为规律的算法，具有自我学习与更新的优点，但在复杂环境中依然存在算法性能的缺陷。而蚁群算法[12-13]是一种模拟蚂蚁觅食行为的启发算法，因其鲁棒性强、易于与其他算法结合等优点而被广泛应用。文献[14-16]通过改进蚁群算法来实现路径上的规划，虽提高了算法的性能，但不能从根本上优化路径，因此，本文提出一种新的自适应蚁群算法，以最短路径长度与最少转折次数为优化目标，改进邻域搜索范围、初始信息素与信息挥发系数，提升算法的性能。

对于路径平滑处理，文献[17-18]分别采用二次优化与删除中间节点的方法，虽有较好的平滑效果，但不能直接作为智能车辆的行驶路径。故本文采用B（B-spline curve）样条曲线平滑处理[19]，考虑车辆非完整约束，使其满足智能车辆转向稳定性及速度和加速度连续性的要求。

1 数学模型

1.1 城市道路环境建模

本文采用广泛应用于路径规划的栅格法，对城市道路环境建模，将城市道路环境简化为网格地图。如图1所示。以4×4栅格环境矩阵G为例，栅格地图由栅格环境矩阵G生成，白色栅格为可行驶区域，即G（m，n）=0，黑色栅格表示被城市建筑、绿化带、车辆等占用的区域，即G（m，n）=1，m、n分别表示矩阵行、列数。

在二维平面上，每个栅格坐标在正交参考系中计算，假设整个栅格用整数标记，长度等于坐标的单位长度，就可以得到以下坐标，表示为：

xi=mod（i，Nx）-0.5yj=mod（j，Ny）-0.5。（1）

式中：i、j分别表示为每行每列栅格序号;Nx、Ny为栅格地图每行每列的栅格数;mod为余数运算。

1.2 问题描述

城市道路中智能车辆的路径长度、转折次数是反映车辆的通行能力的重要指标。因此，可以通过优化路径长度与转折次数，提高车辆的通行能力。

1.2.1 最短路径长度

路径长度决定车辆的通行能力，路径越短，车辆通过能力越好，因此定义行驶路径总长度W目标函数为：

minW=∑Nn=1dnij。（2）

式中：dnij为在第n步时位置i与j之间的步长;N为总步数。

1.2.2 最少转折次数

路径转折次数决定车辆通行的稳定性，规划的转折次数越少车辆越稳定，因此定义路径总累计转折次数P目标函数为：

minP=∑n-1n=0（dn+1-dn）。  （3）

dn+1-dn=0，1，n=0或kn=kn+1kn≠kn+1。 （4）

式中：dn+1-dn為在第n与n+1步时的转折次数，kn、kn+1分别为第n、n+1步时路径的斜率。

1.2.3 总目标优化函数

将最短路径和最少转折次数作为总目标优化，在保证路径最短的同时，有较少的转折次数，从而提高车辆的通行能力。

minZ（n）=ξ1∑Nn=1dnij+ξ2∑n-1n=0（dn+1-dn）。（5）

式中：Z（n）为总目标函数;ξ1、ξ2为路径长度和转折次数的权重。

2 改进的蚁群算法

针对标准蚁群算法（Ant Colony Optimization，ACO）求解路径的节点及转折数较多，且搜索能力与收敛能力不足，做出如下改进：扩大搜索邻域范围，采用A*算法的最短路径全局总代价更新初始蚁群信息素，动态调整信息素挥发系数。

2.1 扩大领域搜索范围

标准蚁群算法中可以沿8个方向转移到相邻的栅格，如图2（a）所示。相邻2个搜索方向的夹角为45°，步长为1、2。在该邻域搜索范围下，规划出的路径节点较多且转折次数多，因此，标准蚁群算法所得路径实际上不是最短的。

针对上述问题，对节点搜索邻域范围改进，如图2（b）所示，在保留当前节点邻域的8个节点为算法的扩展节点的同时，还将当前节点次邻域的16个节点也纳入扩展节点，此时算法搜索邻域节点的个数将扩大到24，节点移动的方向也增加到16个方向，步长为1、2、2、5、22可供选择，扩大邻域搜索的范围。

2.2 自适应蚁群初始信息素

A*算法有避免盲目搜索，提高搜索效率的优点，本文改进算法利用A*算法最短路径得到总代价更新蚁群初始信息素。

A*算法的启发式函数用估计函数表示，公式为：

f（n）=h（n）+g（n）。（6）

式中：h（n）是当前位置到目标位置的代价;g（n）是初始位置到当前位置的代价。

根据A*启发函数得到的最短路径的总代价Cf，将全局引导的蚁群初始信息素设置为：

τ=Q1Cf。（7）

式中：Q1是比例系数，反复实验选取为0.002;τ为蚁群初始信息素。

2.3 自适应信息素挥发系数

标准蚁群算法的信息素挥发系数（ρ）是小于1的常量。当ρ偏大时，路径被再次选择的可能性较大，易出现局部收敛;当ρ偏小时，算法的搜索能力提高，但收敛的速度降低[20]。因此，在算法搜索前期，需要较大的ρ，快速找到优势路径;而在算法搜索后期，需要较小的ρ，扩大全局搜索能力。故本文提出改进的信息ρ与迭代次数u的高斯函数变化关系见公式（8）。

ρ（u）=Ce-（u75）2。 （8）

式中：C为比例系数，经过多次实验，比例系数选取0.5。

2.4 死锁策略

当蚂蚁搜索最优路径时，可能会出现死锁现象，使得蚂蚁在栅格中无法执行下一步动作。针对死锁现象，提出当蚂蚁无法找到起始栅格以外的其他栅格时，可以回到上一栅格位置，并将当前位置从可行栅格剔除，视为障碍栅格，避免出现死锁现象。

2.5 蚁群算法参数校验

启发式因子α、β，是蚂蚁进行路径搜索的重要程度指标，取值直接影响转移概率，信息素启发因子越大，信息素所占比重就越大，从而使得后面蚂蚁放弃新路径的搜索;而信息素过少时，则无法找到全局最优解，因此需要对其进行参数检验。本文实验：选取迭代次数K=100;蚂蚁数量M=50，将α、β分别设置1、2、3、…、10，分别在2种不同环境复杂度下进行仿真。

信息素启发因子对最优路径长度与迭代次数的影响曲线如图3和图4所示。

由图3和图4可见，在2种仿真环境下，当启发式因子α增大时，最短路径长度曲线整体均呈现增大、发散趋势，收敛次数曲线整体均呈现下降趋势，综合分析：当启发式因子α增大时，蚂蚁难以得到全局最优路径，因此α最佳取值范围为[1，2]。而当启发式因子β增大时，最短路径的长度逐渐减少，迭代次数也逐渐减少，综合分析：考虑到启发式因子β过大时，会使蚂蚁在某个局部节点上选择最短路径，因此β最佳取值范围为[7，8]。

3 路径优化处理

改进的自适应蚁群算法在搜索最短路径的过程中，因避开障碍物产生较多的转折角，故不能直接当作车辆的行驶路径[21-22]。而三次B样条曲线在节点处二阶连续，可满足自动驾驶车辆的速度和加速度连续性要求，因此，本文采用三次B样条曲线对路径节点平滑处理。

三次B样条曲线表达式为：

p（t）=∑3i=0piG1，3（t）。   （9）

式中：Gi，3（t）称为基函数。

基函数表示为：

G0，3（t）=16（-t3+3t2-3t+1）

G1，3（t）=16（3t3+6t2+4）

G2，3（t）=16（-3t3+3t2+3t+1）

G3，3（t）=16t3        。 （10）

将公式（10）带入公式（9）得到曲线段P0，3（t）为：

P0，3（t）=161tt2t3T1410-30303-630-13-31P0P1P2P3，t∈[0，1]。（11）

由于智能车辆是非完整约束，三次B样条处理的路径曲率必须满足车辆的约束：κ≤tanδL，δ为前轮摆角，L为轴距。

4 仿真实验

利用MATLAB进行仿真实验，在不同复杂程度、规模大小的城市道路环境模型下，将本文改进自适应蚁群算法与其他算法比较实验。由于城市道路是动态的，不能直观体现改进算法的性能，因此本文将选取某一时刻下的城市道路环境进行仿真实验。经初步实验，在栅格地图中，Nx=20，Ny=20，初始点坐标为xi=0.5，yj=19.5，目标点坐标为xi=19.5，yj=0.5，改进蚁群的参数设置：迭代次数K=100;蚂蚁数量M=50;选取信息素重要性因子α为1.5;选取启发式重要性因子β为7;初始信息素的比例系数C=0.5;信息素挥发系数的比例系数Q1=0.002。

4.1 城市道路环境模型下算法比较

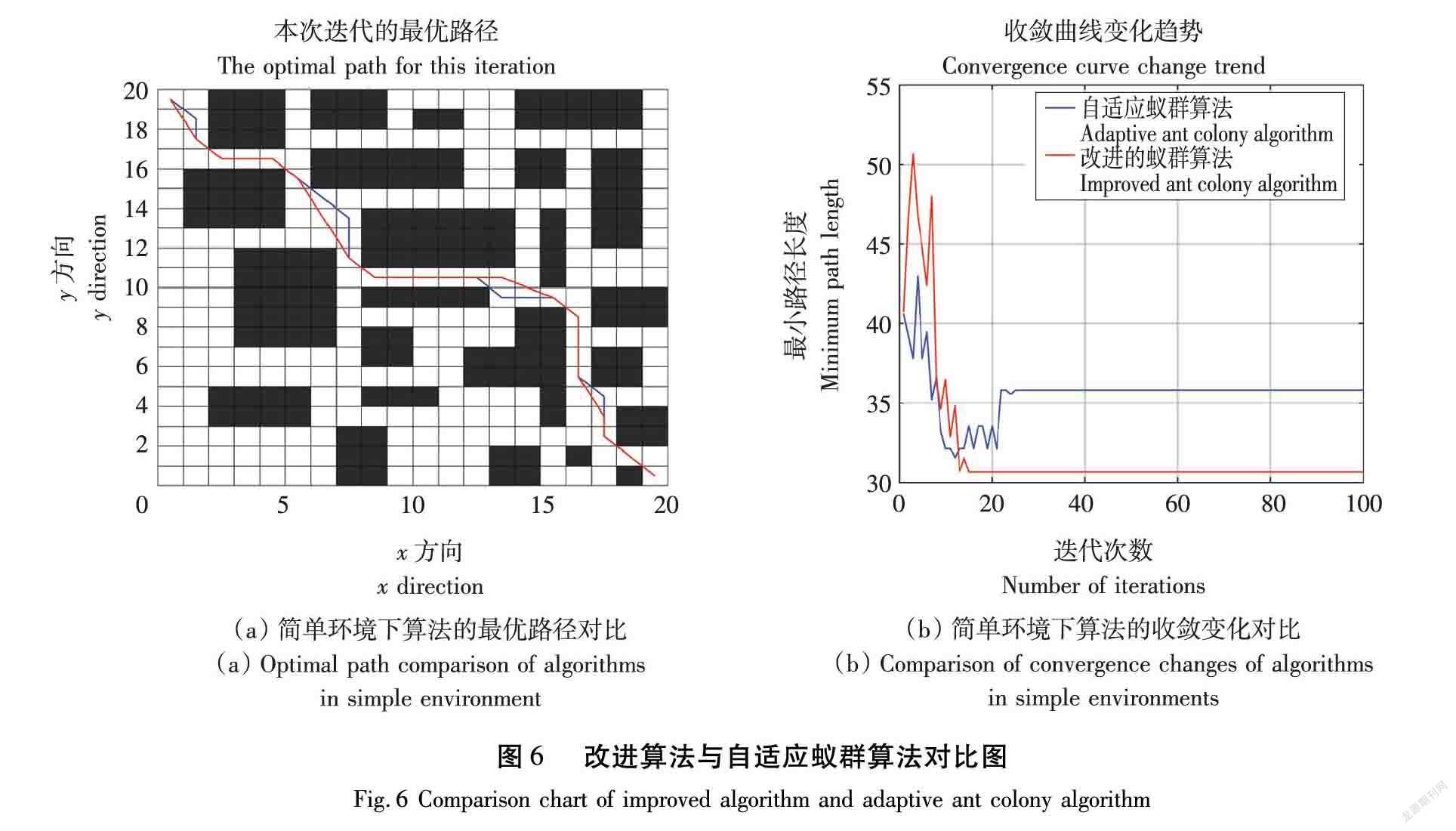
在由环境矩阵G生成栅格环境地图，选取标准蚁群算法，该算法环境为复杂的城市道路环境模型，其运行结果与本文改进算法路径对比，如图5所示。其次，选取自适应蚁群算法，该算法环境为简单城市道路环境模型，其运行结果与本文改进算法路径对比，如图6所示。

最优路径与收敛代数是衡量蚁群算法的2个重要指标，将算法均独立运行20次，比较仿真结果，见表1。改进的算法中将A*算法启发式函数与蚁群算法初始信息素相结合，动态的更新信息素挥发系数，使得算法具有更高的搜索能力和更快的收敛速度。较标准蚁群算法最小收敛代数平均值减少37.5%，较自适应蚁群算法最小收敛代数平均值减少20%;扩大蚁群算法中搜索邻域搜索范围，有效地缩短路径的长度。较标准蚁群算法最优路径缩短3.89%，比较自适应蚁群算法最优路径缩短8.37%。改进的蚁群算法中路径节点较标准蚁群算法减少28%，较自适应蚁群算法减少24.2%，由图5和图6可直观看出路径转折次数减少，路面更加平缓。

4.2 平滑实验

采用三次B样条曲线平滑处理改进蚁群算法的最优路径，仿真结果如图7所示。可见，采用三次B样条处理后的路径转折角度进一步减少，路径整体更加平滑，满足智能车辆速度与加速度连续性的要求，保证车辆平稳运行。

5 结论

为了优化城市道路中智能车辆的路径，提出改进的自适应蚁群算法，得出以下结论。

（1）通过优化目标函数，改进领域搜索范围，能有效缩短路径长度及转折数，提高智能车辆的通行能力。

（2）改进蚁群初始信息素和信息挥发系数，加快全局搜索能力和收敛速度，提高智能车辆的实时性。

（3）采用B樣条曲线平滑处理所得路径，保证智能车辆转向的稳定性及安全性。

改进算法虽较好地降低收敛代数，但受邻域搜索方式影响，前期最短路径长度较长，因此，可对该方面不足继续深入研究。

【参 考 文 献】

[1]丁柏群，姜瑾.基于蚁群算法和动态路阻的物流配送路径优化[J].森林工程，2014，30（2）：149-152.

DING B Q， JIANG J. Path optimization of logistics distribution vehicle based on ant colony algorithm and dynamic road impedance[J]. Forest Engineering， 2014， 30（2）： 149-152.

[2]肖广兵，王蓝仪，孙宁，等.基于车路协同的地下停车场车辆定位算法发散性研究[J].计算机应用研究，2021，38（2）：530-533.

XIAO G B， WANG L Y， SUN N， et al. Divergence of cooperative vehicle localization in underground parking lots[J]. Application Research of Computers， 2021， 38（2）： 530-533.

[3]XIAO G B， ZHANG H B， SUN N， et al. Cooperative link scheduling for RSU-assisted dissemination of basic safety messages[J]. Wireless Networks， 2021， 27（2）： 1335-1351.

[4]汤红杰，王鼎，皇攀凌，等.优化dijkstra算法在工厂内物流AGV路径规划的研究[J].机械设计与制造，2018（S1）：117-120.

TANG H J， WANG D， HUANG P L， et al. AGV path planning based on optimized dijkstra algorithm in logistics factory[J]. Machinery Design & Manufacture， 2018（S1）： 117-120.

[5]郑琰，黄兴，潘颖.城市应急物流中心多目标选址模型及方法研究[J].重庆理工大学学报（自然科学），2020，34（6）：239-246.

ZHENG Y， HUANG X， PAN Y. Research on the multi-objective facility location model for urban emergency logistics centers[J]. Journal of Chongqing University of Technology （Natural Science）， 2020， 34（6）： 239-246.

[6]宋宇，王志明.改进A星算法移动机器人路径规划[J].长春工业大学学报，2019，40（2）：138-141.

SONG Y， WANG Z M. Path planning simulation based on improved A star algorithm[J]. Journal of Changchun University of Technology， 2019， 40（2）： 138-141.

[7]杨艳艳，马成林，王怡菲，等.基于禁忌搜索带时间窗与车载约束的配送路线研究[J].森林工程，2018，34（3）：100-106.

YANG Y Y， MA C L， WANG Y F， et al. Research on distribution route with time window and on-board constraint based on tabu algorithm[J]. Forest Engineering， 2018， 34（3）： 100-106.

[8]袁佳泉，李胜，吴益飞，等.基于模拟退火蚁群算法的机器人路径规划方法[J].计算机仿真，2019，36（10）：329-333.

YUAN J Q， LI S， WU Y F， et al. Robot path planning method based on simulated annealing ant colony algorithm[J]. Computer Simulation， 2019， 36（10）： 329-333.

[9]《中国公路学报》编辑部.中国汽车工程学术研究综述·2017[J].中国公路学报，2017，30（6）：1-197.

Editorial Department of China Journal of Highway and Transport. Review on Chinas automotive engineering research progress： 2017[J]. China Journal of Highway and Transport， 2017， 30（6）： 1-197.

[10]邓高峰，张雪萍，刘彦萍.一种障碍环境下机器人路径规划的蚁群粒子群算法[J].控制理论与应用，2009，26（8）：879-883.

DENG G F， ZHANG X P， LIU Y P. Ant colony optimization and particle swarm optimization for robot-path planning in obstacle environment[J]. Control Theory & Applications， 2009， 26（8）： 879-883.

[11]周文璐，林萍，徐曉美，等.黄麻纤维毡吸声特性及其在汽车上的应用[J].林业工程学报，2021，6（3）：113-119.

ZHOU W L， LIN P， XU X M， et al. Sound absorption characteristics of the jute fiber felt and its application in automobiles[J]. Journal of Forestry Engineering， 2021， 6（3）： 113-119.

[12]RESHAMWALA A， DEEPIKA P. Robot path planning using an ant colony optimization approach： a survey[J]. International Journal of Advanced Research in Artificial Intelligence， 2013， 2（3）：65-71.

[13]李燕，季建楠，沈葭栎，等.基于改进蚁群算法的移动机器人路径规划方法[J].南京信息工程大学学报（自然科学版），2021，13（3）：298-303.

LI Y， JI J N， SHEN J L， et al. Mobile robot path planning based on improved ant colony algorithm[J]. Journal of Nanjing University of Information Science & Technology （Natural Science Edition）， 2021， 13（3）： 298-303.

[14]赵静，汤云峰，蒋国平，等.基于改进蚁群算法的移动机器人路径规划[J].南京邮电大学学报（自然科学版），2019，39（6）：73-78.

ZHAO J， TANG Y F， JIANG G P， et al. Mobile robot path planning based on improved ant colony algorithm[J]. Journal of Nanjing University of Posts and Telecommunications （Natural Science Edition）， 2019， 39（6）： 73-78.

[15]徐玉琼，娄柯，李婷婷，等.改进自适应蚁群算法的移动机器人路径规划[J].电子测量与仪器学报，2019，33（10）：89-95.

XU Y Q， LOU K， LI T T， et al. Path planning of mobile robot based on improved adaptive ant colony algorithm[J]. Journal of Electronic Measurement and Instrumentation， 2019， 33（10）： 89-95.

[16]辜勇，段晶晶，苏宇霞，等.基于改进蚁群算法的仓储物流机器人路径规划[J].武汉理工大学学报（交通科学与工程版），2020，44（4）：688-693，697.

GU Y， DUAN J J， SU Y X， et al. Path planning of warehouse logistics robot based on improved ant colony algorithm[J]. Journal of Wuhan University of Technology （Transportation Science & Engineering）， 2020， 44（4）： 688-693， 697.

[17]赵晓，王铮，黄程侃，等.基于改进A*算法的移动机器人路径规划[J].机器人，2018，40（6）：903-910.

ZHAO X， WANG Z， HUANG C K， et al. Mobile robot path planning based on an improved A* algorithm[J]. Robot， 2018， 40（6）： 903-910.

[18]周兵，萬希，吴晓建，等.紧急避撞工况下的路径规划与跟踪[J].湖南大学学报（自然科学版），2020，47（10）：10-18.

ZHOU B， WAN X， WU X J， et al. Path planning and tracking in scenario of emergency collision avoidance[J]. Journal of Hunan University （Natural Sciences）， 2020， 47（10）： 10-18.

[19]史恩秀，陈敏敏，李俊，等.基于蚁群算法的移动机器人全局路径规划方法研究[J].农业机械学报，2014，45（6）：53-57.

SHI E X， CHEN M M， LI J， et al. Research on method of global path-planning for mobile robot based on ant-colony algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery， 2014， 45（6）： 53-57.

[20]李冰林，徐晓美，吕立亚，等.基于分数阶微积分的爆胎汽车横向稳定性控制[J].安全与环境学报，2018，18（6）：2219-2224.

LI B L， XU X M， LYU L Y， et al. On the lateral stability control of a blownout vehicle based on the fractional calculus[J]. Journal of Safety and Environment， 2018， 18（6）： 2219-2224.

[21]张磊，徐晓美，潘健，等.半挂汽车列车高速侧倾稳定性控制研究[J].制造业自动化，2019，41（12）：99-102.

ZHANG L， XU X M， PAN J， et al. Roll stability control of the truck semi-trailer at high speed[J]. Manufacturing Automation， 2019， 41（12）： 99-102.