高速铁路独塔斜拉桥主塔索鞍区域空间应力分析

王立峰 孟祥冬 付宁 刘龙

摘 要：以（120+120）m独塔斜拉T构组合桥为背景，研究分丝管索塔锚固区混凝土及索鞍应力分布规律。采用ABAQUS软件建立索塔节段局部有限元模型，通过模拟斜拉索与索鞍的接触关系，研究索塔锚固区混凝土与索鞍的空间应力分布状态，并与等效面荷载分析方式进行对比分析。结果表明：接触分析比面荷载分析更接近实际受力情况，可更准确模拟出斜拉索的横向变形，及受到的索塔两侧不平衡索力的影响。此结果为同类型桥梁索鞍区域受力分析提供参考。

关键词：铁路桥梁;索塔锚固区;数值计算;分丝管;索鞍;有限元

中图分类号：U448.27;U441     文献标识码：A   文章编号：1006-8023（2022）01-0132-07

Spatial Stress Analysis of Main Tower Cable Saddle Area of Single

Tower Cable Stayed Bridge on High Speed Railway

WANG Lifeng1， MENG Xiangdong1， FU Ning2， LIU Long1

（1.School of Civil Engineering， Northeast Forestry University， Harbin 150040， China;

2.China Railway 22nd Bureau Group Co.， Ltd.， Beijing 100043， China）

Abstract：Taking （120+120） m single-tower cable-stayed T structure composite bridge as the background， the stress distribution of concrete and cable saddle in the anchorage zone of filament pipe and cable tower was studied. The local finite element model of the cable pylon segment was established by ABAQUS software. By simulating the contact relationship between the cable and the cable saddle， the spatial stress distribution state of the concrete and the cable saddle in the anchor zone of the cable pylon was studied and compared with the equivalent surface load analysis method. The results showed that the contact analysis was closer to the actual force situation than the surface load analysis， and can accurately simulate the transverse deformation of the cable and the influence of unbalanced cable forces on both sides of the cable pylon.

Keywords：Railway bridge; anchorage zone of pylon; numerical calculation; filament pipe; cable saddle; finite element

0 引言

索塔锚固区是斜拉桥结构中承受较大集中力的部位，其空间应力分布极为复杂[1]。目前常用的斜拉索锚固形式有钢锚梁锚固形式、钢锚箱锚固形式、预应力锚固形式和索鞍锚固形式等。钢锚梁锚固是在塔柱内壁设置混凝土牛腿或钢牛腿支撑钢锚梁承受斜拉索拉力，传递至牛腿的索力最终通过剪力钉传递到塔柱混凝土;钢锚箱是由垫板、承压板、腹板、壁板、横隔板、开孔板、连接板及加劲肋等组成的空间箱形结构，斜拉索水平分力由锚箱壁板承担，竖向分力通过嵌入混凝土桥塔的开孔板传递至塔柱;预应力锚固是通过在索塔锚固区设置预应力筋预先对索塔施加压力，再将斜拉索直接锚固在索塔内侧;索鞍锚固是在塔端布置平行导向管，钢绞线分别穿过对应的钢管互不干涉，形成分离布置，通过索鞍均匀分散地将索力传递至桥塔[2-4]。由于索鞍锚固形式可有效解决混凝土拉应力过大和钢绞线打绞等问题，加之施工简便，受力明确，并且方便单根钢索更换，在斜拉桥中得到广泛应用。

索塔锚固区受到斜拉索的局部集中力及孔洞削弱等因素影响而处于复杂受力状态，在设计时必须保证锚固区结构的极限承载力及足够的抗裂储备;同时要保证索力的传递和平衡简单、可靠，避免塔柱受扭[5];锚固构造细节的设计必须考虑斜拉索张拉、锚固的简易性和经济性[6];锚固区构造必须具备可接近性，使检查养护人员便于操作，为换索提供必要条件[7]。承压区应力理论分析时，主要通过实验室内的缩尺节段模型试验来完成，可对锚固区域主要因素进行独立控制，但成本较高[8];解析计算则通过对结构进行一定简化，建立满足边界以及荷载作用条件下的应力计算公式，但由于土木工程的一些不确定因素，输入参数难以精确，计算复杂且精度较差[9];有限元分析通过建立板壳有限元模型或实体单元的三维有限元模型进行数值分析，按实际情况在指定部位施加邊界条件及外部荷载，具有成本低及计算准确的优点[10]。

刘尊稳等[11]通过建立京沪高铁津沪联络线特大桥主桥分丝管索鞍区的ANSYS有限元模型，研究索鞍周围混凝土应力的分布规律及其极限荷载;张少华[12]利用ABAQUS模拟某矮塔斜拉桥索鞍锚固区，探讨了有限元联合仿真的思路及等效均匀面荷载和等效线性面荷载作用模式下索塔混凝土的主要分析结果。随着有限元建模技术的不断发展，有限元仿真已成为对应力复杂区域分析的最有效手段。

由以上文献可知，以往研究多以常规斜拉桥结构为研究对象，斜拉T构组合桥索鞍接触分析相关的研究鲜见报道。本文以拟建杭温铁路楠溪江大桥为研究对象，利用ABAQUS数值模拟手段建立主塔索鞍锚固区仿真模型，考虑索鞍对混凝土受集中力的分散作用，建立接触单元对斜拉索与索鞍进行非线性接触分析，并与常规的等效面荷载模型进行对比，探讨了索塔锚固区混凝土及索鞍应力分布规律，为同类型桥梁索鞍区域受力分析提供参考。

1 工程概况

1.1 工程概况

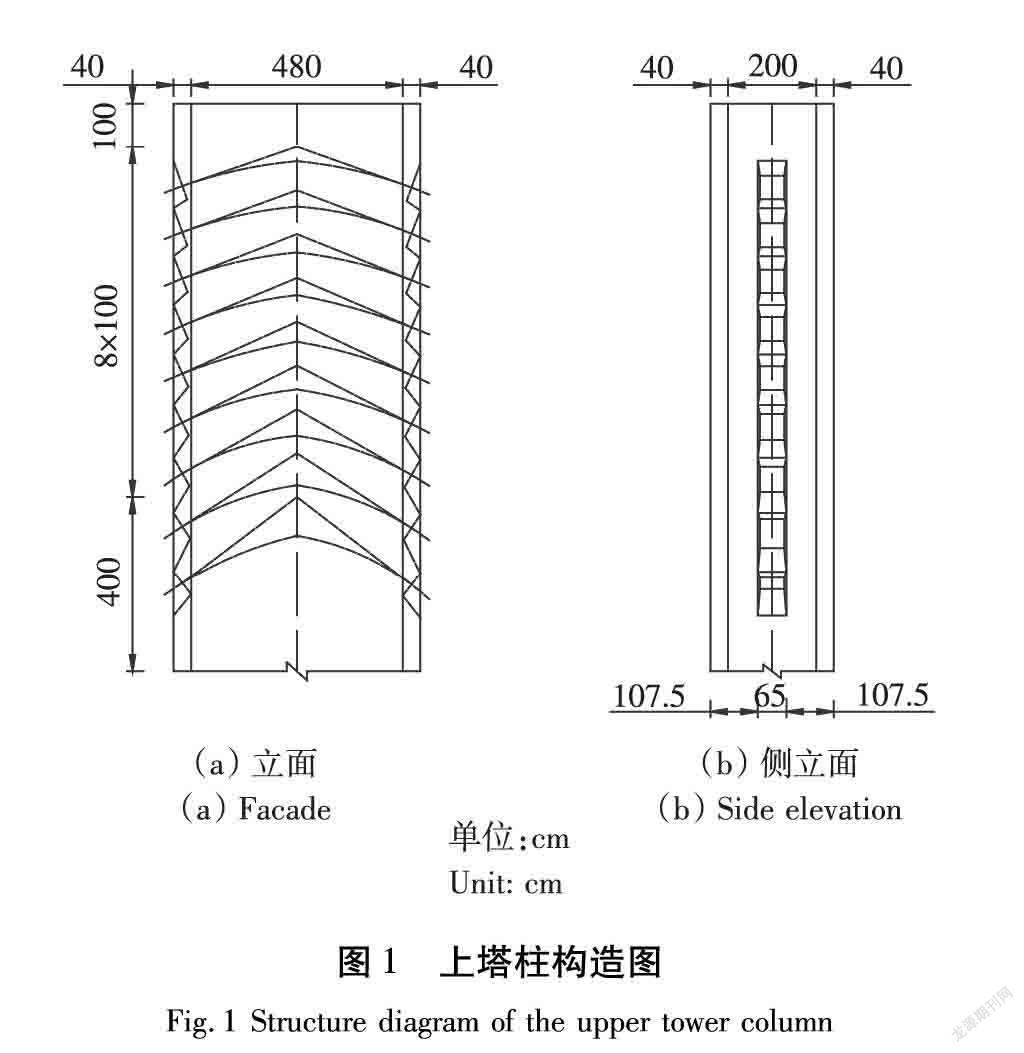
新建杭温铁路楠溪江大桥上部结构采用（120+120）m独塔斜拉T构组合桥，主桥长241.5 m。设计车速350 km/h，采用双线ZK活载（中国客运规定的活荷载）。全桥共18根斜拉索，采用空间双索面体系，斜拉索梁上间距分别为8 m和8.3 m，在塔端采用分丝管索鞍贯通，间距为1.0 m，张拉端设置在梁上。斜拉索最长为212 m，最短为89 m，采用单根张拉。索塔采用C50钢筋混凝土，设置于桥面两侧，桥面以上索塔高度为35 m。索塔采用矩形实体截面，顺桥向宽5.6 m，横桥向宽2.8 m。索塔上塔柱构造如图1所示。

1.2 计算假定

采用ABAQUS建立索塔锚固区有限元模型，为简化模型易于收敛，索塔及分丝管索鞍假定如下。

（1）接触分析利用等效原理将分丝管索鞍构造简化为一束，拉索作用在索鞍上，考虑其接触关系，索力换算为面荷载施加在拉索两端。

（2）面荷载分析忽略索力变化和索塔两侧不平衡索力的影响，由平衡条件将拉索径向线压力等效为q=F/R，然后再将径向均布力等效加載到索鞍圆弧段下半部分的单元面上，各索鞍等效压力值见表1。

（3）忽略索塔内钢筋的影响。

（4）索塔顶部自由，底部固结。

1.3 有限元模型建立

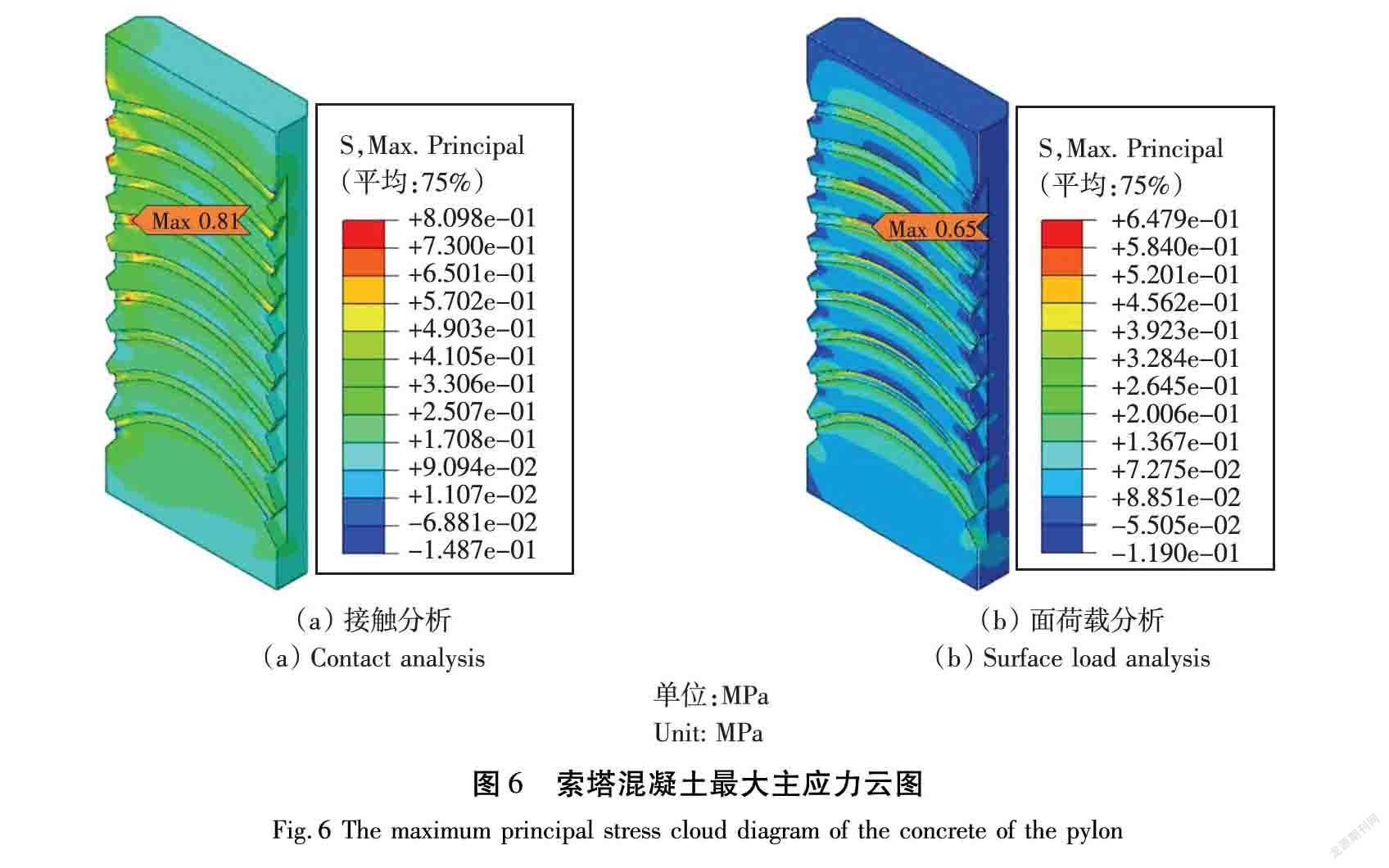
运用ABAQUS建立索塔锚固区局部精细模型，索塔及索鞍网格划分情况如图2所示，混凝土结构和索鞍结构选用减缩积分的C3D8R六面体及C3D6楔形实体单元模拟，斜拉索选择C3D8R六面体单元模拟。索鞍与外围混凝土采用共节点方式模拟其接触关系，拉索与索鞍间采用通用接触模拟，分别定义法向与切向属性为硬接触与罚摩擦，进行有限元数值模拟，接触分析与面荷载分析比较见表2。

1.4 本构模型

混凝土的破坏形式取决于应力条件与材料强度，分为剪切破坏和拉伸破坏2种形式，对于不同的破坏形式应采用相应的强度条件，本文主要研究内容为索塔锚固区应力分析，考虑索鞍周围混凝土的横向拉伸破坏，故采用塑性损伤本构关系模型。混凝土单轴拉压应力（σ）-应变（ε）曲线依据《混凝土结构设计规范》（GB 50010—2010）按下列公式确定：

σt=1-dtEcε。 （1）

σc=1-dcEcε。（2）

式中：dt、dc分别为混凝土单轴受拉和受压损伤演化参数; Ec为弹性模量，取3.45×104 MPa。

C50混凝土应力-应力变曲线如图3所示。

参考《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）第6.3.3条规定，混凝土主拉应力σtp和主压应力σcp按公式（3）和公式（4）计算：

σtp=σx+σy2-σx-σy22+τ2。  （3）

σcp=σx+σy2+σx-σy22+τ2。  （4）

对于混凝土一点处的应力状态，可通过公式（3）及公式（4）将计算弯矩产生的混凝土法向应力σx和竖向压应力σy转换为第一、三主应力。

斜拉桥分丝管索鞍为金属材料，拉伸及压缩强度均较高，本构关系采用单折线模型，弹性模量Es取2.06×105 MPa。

本文使用第一强度理论，即以最大拉应力强度理论作为破坏发生的判断依据，认为混凝土及索鞍一点处承受的最大主拉应力达到其材料的极限应力时，材料断裂破坏。

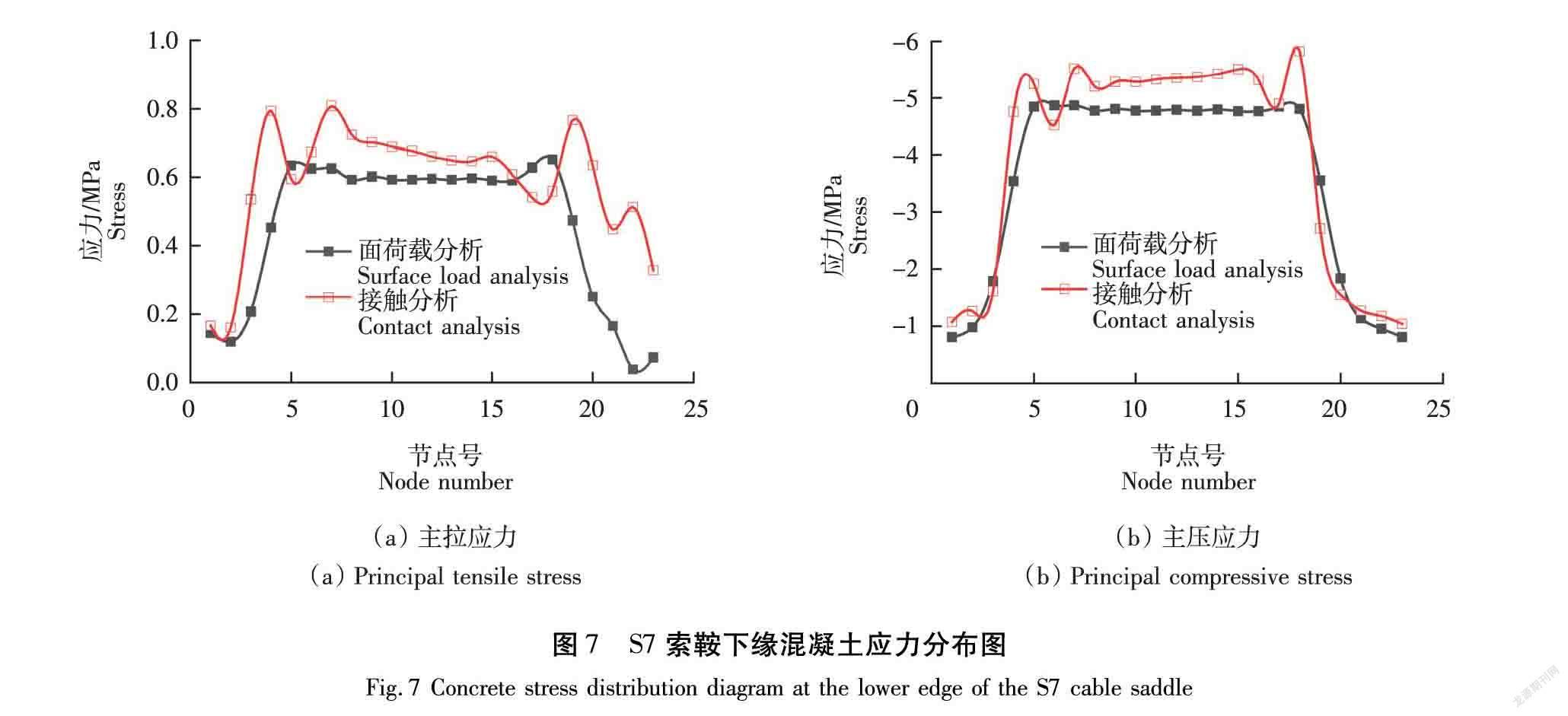
2 有限元模型验证

根据ABAQUS有限元模型计算结果，混凝土桥塔竖向应力沿索塔高度分布如图4所示。接触分析与面荷载分析时索塔底部的竖向压应力均在3.8 MPa左右，其数值与全桥有限元模型计算结果中塔底竖向压应力一致。由图4可知，索塔锚固区塔身混凝土在各工况下竖向均受压，当0≤h≤20 m时，索塔应力为3.2～3.8 MPa;当20 m

2种分析方式所得竖向变形如图5所示。接触分析与面荷载分析时竖向位移随桥塔高度上升均匀增加，塔顶最大竖向位移分别为-3.609 mm和-3.674 mm，两者变形分布规律基本一致，接触分析时桥塔中部竖向变形略大于两端，已有研究表明，斜拉索作用于索鞍上的荷载沿孔道方向成2次抛物线形状分布[13-14]，索鞍中心区域荷载大于两侧，接触分析较好地模拟出索力沿索鞍轴线不均匀的分布状况。

3 索塔混凝土局部应力分析

为更直观地研究索塔锚固区的各项应力分布，沿纵桥向索塔孔道中线取剖断面进行分析，应力分布如图6所示。接触分析与面荷载分析时混凝土应力分布情况极为相似，最大主压应力出现在S3索鞍下混凝土拐角处;索鞍外围混凝土会在S6索鞍端部极小范围内出现一定的主拉应力，接触分析与面荷载分析时主拉应力最大值分别为0.81 MPa和0.65 MPa，小于C50混凝土轴心抗拉强度值2.65 MPa，且很快扩散均匀。索鞍外围混凝土在实际设计及施工时配置了加强普通钢筋，可有效抑制或避免混凝土主拉应力的出现。

图7列出了索力最大的S7索鞍下缘中心线混凝土的主应力情况。通过接触分析和面荷载分     析2种方法的结果对比可知，两者的主应力分布规律一致，接触分析偏大约8.4%。主拉应力在接触分析索鞍圆弧段两侧出现应力集中，产生这种现象的主要原因为斜拉索，同时受到摩擦及索塔两侧不平衡索力的影响，而按面荷载分析时计算结果偏小。在工程设计运用中，相对面荷载分析方法，接触分析方法更接近于索塔的实际受力情况，可提供更可靠的设计依据。

4 索鞍应力分析

接触分析与面荷载分析时索鞍有限元计算结果如图8所示。主拉应力云图显示，在成桥索力下，2种分析方式时索鞍所承受的最大拉应力均不超过30 MPa，远小于钢材的极限强度值。接触分析中索鞍最大拉应力主要集中在索鞍两端与斜拉索接触处，原因为该区域拉索受拉方向与索鞍轴线存在一定偏角而产生应力集中，而面荷载分析中索鞍两端应力接近零，接触分析更符合实际受力情况。除索鞍两端应力集中区域外，接触分析时索鞍主拉应力值为1.99～13.78 MPa，最大拉应力出现在S9索鞍圆弧段末端，与面荷载分析时应力分布基本一致。

选取索力最大的S7索鞍纵向底面中心线位置为研究对象，对索鞍主应力的计算结果进行比较，如图9所示。通过对比可知。面荷载分析时拉压主应力在索鞍圆弧段沿长度方向基本保持不变，两侧直线段迅速减小至零;接触分析时索鞍圆弧段中心区域应力分布均匀，但在两端直线段应力集中现象明显。两种分析方式的主压应力分布规律基本一致，而接触分析时主拉应力较大，其值约为面荷载分析的2倍，主要表现为横向拉应力，最大值达到8.96 MPa，可见接触分析模拟的实体斜拉索单元承受荷载时发生横向变形，在索鞍截面上产生不均匀应力。

5 结论

采用有限元方法对楠溪江大桥索塔锚固区进行了空间应力分析，对比接触分析和面荷载分析2种模拟方式的应力分布规律，得到以下结论。

（1）索鞍外围混凝土仅会在S6索鞍端部极小范围区域内出现主拉应力，约占整个区域的0.3%，影响较小。接觸分析和面荷载分析时最大主拉应力分别为0.81MPa和0.65MPa，均小于C50混凝土抗拉强度设计值。索鞍外围混凝土在实际设计及施工时配置了加强普通钢筋，可有效抑制或避免混凝土主拉应力的出现。

（2）接触分析时实体斜拉索单元受拉发生横向变形，索鞍主拉应力最大值达到8.96 MPa，约为面荷载分析的2倍。因此，接触分析模拟了索鞍截面上产生的不均匀应力，面荷载分析得到的计算结果偏小。

（3）接触分析可更准确地模拟斜拉索受到的摩擦及索塔两侧不平衡索力，索塔主应力较面荷载分析偏大8.4%，且索鞍圆弧段两侧明显应力集中，相比面荷载分析，接触分析更符合实际情况。

【参 考 文 献】

[1]毛伟琦，胡雄伟.中国大跨度桥梁最新进展与展望[J].桥梁建设，2020，50（1）：13-19.

MAO W Q， HU X W. Latest developments and prospects for long-span bridges in China[J]. Bridge Construction， 2020， 50（1）： 13-19.

[2]殷鹏程.福厦高铁湄洲湾跨海大桥（96+180+96）m斜拉桥总体设计[J].铁道标准设计，2020，64（S1）：12-18.

YIN P C. Overall design of （96+180+96） m cable stayed bridge of Meizhou bay sea crossing bridge on Fuzhou-Xiamen high-speed railway[J]. Railway Standard Design， 2020， 64（S1）： 12-18.

[3]延力强.空间索面斜拉桥索塔锚固方案研究[J].铁道标准设计，2014，58（9）：75-79.

YAN L Q. Study on anchoring scheme for cable-pylon of cable-stayed bridge with spatial cable plane[J]. Railway Standard Design， 2014， 58（9）： 75-79.

[4]支燕武.一种新型斜拉桥索-塔锚固结构的设计研究[J].铁道工程学报，2018，35（10）：49-52，98.

ZHI Y W. Research on the design of a new type of cable-tower anchorage structure of cable-stayed bridge[J]. Journal of Railway Engineering Society， 2018， 35（10）： 49-52， 98.

[5]肖纬，王志强，魏红一.考虑缆索滑移的精细化索鞍模型[J].石家庄铁道大学学报（自然科学版），2016，29（2）：22-27.

XIAO W， WANG Z Q， WEI H Y. Detailed saddle model considering stick-slip of the cable[J]. Journal of Shijiazhuang Tiedao University （Natural Science Edition）， 2016， 29（2）： 22-27.

[6]付小军.普速铁路单线独塔斜拉桥总体设计及创新[J].铁道标准设计，2019，63（11）：60-65.

FU X J. Overall design and innovation of single tower cable-stayed bridge on conventional railway[J]. Railway Standard Design， 2019， 63（11）： 60-65.

[7]张海文，李亚东.矮塔斜拉桥索鞍混凝土局部应力分析[J].铁道标准设计，2009，53（1）：42-44.

ZHANG H W， LI Y D. Analysis on partial stress of cable straddle concrete for low-tower cable stayed bridge[J]. Railway Standard Design， 2009， 53（1）： 42-44.

[8]陈再现，刘兆锰，孙凯林，等.缩尺模型混合模拟试验测量误差分析及试验验证[J].建筑结构学报，2017，38（8）：167-174.

CHEN Z X， LIU Z M， SUN K L， et al. Measurement error analysis and experimental verification of hybrid simulation testing method for reduced scale model[J]. Journal of Building Structures， 2017， 38（8）： 167-174.

[9]徐艷，童川，李建中.漂浮体系斜拉桥黏滞阻尼器参数的简化计算[J].同济大学学报（自然科学版），2018，46（5）：574-579，638.

XU Y， TONG C， LI J Z. Simplified calculation of viscous damper parameter for floating-system cable-stayed bridge[J]. Journal of Tongji University （Natural Science）， 2018， 46（5）： 574-579， 638.

[10]陈康明，吴庆雄，黄汉辉.斜拉桥桥塔节段力学性能[J].交通运输工程学报，2016，16（5）：17-29.

CHEN K M， WU Q X， HUANG H H. Mechanical property of segmental tower of cable-stayed bridge[J]. Journal of Traffic and Transportation Engineering， 2016， 16（5）： 17-29.

[11]刘尊稳，陈兴冲，张永亮，等.矮塔斜拉桥分丝管索鞍区受力特征研究[J].桥梁建设，2018，48（5）：69-74.

LIU Z W， CHEN X C， ZHANG Y L， et al. Study of mechanical characteristics for strand deviating saddle zone of extra-dosed cable-stayed bridge[J]. Bridge Construction， 2018， 48（5）： 69-74.

[12]张少华.分丝管型索鞍锚固区局部应力简化模拟[J].重庆交通大学学报（自然科学版），2019，38（4）：29-34.

ZHANG S H. Simplified simulation of local stress in anchorage zone with strand-separating saddle[J]. Journal of Chongqing Jiaotong University （Natural Science）， 2019， 38（4）： 29-34.

[13]蔡晓明，张立明，何欢.矮塔斜拉桥索鞍受力分析[J].公路交通科技，2006，23（3）：53-55，59.

CAI X M， ZHANG L M， HE H. Analysis of saddle structures in low tower cable-stayed bridge[J]. Journal of Highway and Transportation Research and Development， 2006， 23（3）： 53-55， 59.

[14]杨相展，易壮鹏，陈洪伟.辅助索对无背索斜拉桥动力学特性的影响[J].公路工程，2021，46（3）：244-249.

YANG X Z， YI Z P， CHEN H W. The effect of cross ties on the dynamic properties of cable-stayed bridge without back-stays[J]. Highway Engineering， 2021， 46（3）： 244-249.