冻黏土与结构接触界面层单剪损伤模型

孙厚超 杨平 卜迎春 石飞停

摘 要：为探究冻土界面层单剪损伤力学特性，本文根据冻黏土与结构接触界面层单剪力学特性试验结果，基于经典的摩尔库仑准则，将内聚力与摩擦系数作为一个与应力第一不变量相关的函数，建立适合于描述冻土材料破坏的本构模型。通过冻土界面层单剪损伤分析，在模型中引入塑性和损伤等内变量，同时建立与温度和粗糙度等相关影响因素的关系，根据热力学第二定律和正交法则，构建用于描述冻土与结构接触界面层单剪的弹塑性损伤模型。采用开发的冻土界面层单剪本构模型，给出相关的数值求解格式，对于各种工况下所反映出的力学特征进行有限元计算分析，与冻土界面层单剪物理试验进行对比验证，结果表明，所建模型是准确合理的。

关键词：接触界面层;冻黏土;抗剪强度;单调剪切;损伤模型

中图分类号：TU435    文献标识码：A   文章编号：1006-8023（2022）01-0115-09

A Damage Model for Frozen Soil-structure Interface Layer

under Monotonic Shearing

SUN Houchao1， YANG Ping2*， BU Yingchun1， SHI Feiting1

（1.College of Civil Engineering， Yancheng Institute of Technology， Yancheng 224051， China;

2.College of Civil Engineering， Nanjing Forestry University， Nanjing 210037， China）

Abstract：In order to explore the mechanical characteristics of monotonic shear damage of frozen soil interface layer， according to the test of mechanical properties of frozen soil-structure interface and classical Mohr-Coulomb criterion， internal cohesion and friction coefficient are assumed to be a function related to the first invariant of stress， then a constitutive model suitable for describing the failure of frozen soil materials is established. Based on the monotonic shear damage analysis of frozen soil interface layer， some intrinsic variables such as plasticity and damage are introduced into the model， and the relationship between temperature and roughness is established. According to the second law of thermodynamics and orthogonal law， an elastic-plastic damage model is established to describe the monotonic shear layer at the interface between frozen soil and structure. The monotonic shear constitutive model of frozen soil interface layer is developed， and the numerical solution format is given. Comparison of finite element analysis and experimental results under various working conditions shows that the proposed model yields good results.

Keywords：Interface layer; frozen soil; shear strength; monotonic shear; damage model

0 引 言

接触界面层模型成为研究土与结构相互作用的重要问题之一。国内外学者已经通过常温土接触面模型试验研究，建立了理想模型、非线性弹性模型、弹塑性模型和损伤模型等接触面本构模型[1-2]。Clough等[3]基于直剪试验建立接触面剪应力与相对切向位移的双曲线模型;Brandt[4]在试验数据分析基础上构建（τ（剪切应力）/σ（正应力）-ω（摩擦力））曲线的两折线简化模型; Mortara等[5]通过接触面循环加卸载力学試验，提出简单弹塑性接触面本构模型;Desai等[6]在接触面本构关系中引入损伤，开辟接触面研究新思路;陈慧远[7]研究表明，当剪切应力（τ）小于摩擦力（ω）时，τ-ω为线弹性关系，相反，当剪切应力大于或等于摩擦力时，接触面进入摩擦滑移阶段，τ-ω为塑性关系;钱家欢[8]通过试验和理论研究表明，接触面的相对位移与应力呈黏弹塑性关系;卢廷浩等[9]在单调剪切试验基础上，利用耦合法向和切向变形，建立了接触面二维、三维本构模型;HU等[10]在直剪试验的基础上，建立能模拟粗糙接触面应力弱化和剪胀现象的损伤力学模型;张嘎等[11]通过大量接触面试验总结粗粒土与结构接触面静、动力学特性规律，建立了粗粒土与结构接触面弹塑性损伤模型。

已有的描述接触面力学行为的本构模型主要是在常温条件下建立的，有关冻土与结构接触界面层本构模型鲜见报道。鉴于冻土与常温土在力学行为上存在巨大差异，冻土与结构接触界面层单调剪切初期存在一个明显最大剪应力，随后接触界面层剪应力迅速衰减到一个相对较小稳定数值，直至剪切结束。用充分考虑土的黏聚力和内摩擦角的摩尔库仑破坏准则对于冻土界面层的破坏模型描述会存在较大偏差，因此，建立冻土与结构接触界面层单剪损伤模型很有必要，也是重要的科学问题。

1 模型建立方法和过程

根据冻土与结构接触界面层力学特性试验结果建立适合于描述冻土材料破坏的本构模型，并在模型中引入损伤和塑性等内变量，同时建立与温度和粗糙度等相关影响因素的关系。将冻土界面层本构模型嵌入其中，给出相关的数值求解格式。通过开发的冻土界面层本构模型对于各种工况下所反映出的力学特征进行有限元计算分析，来进一步验证所开发的本构模型可行性。

试验采用课题组自行研制的冻土与结构接触界面层力学试验仪[12]，该设备配有加荷、温控和数据采集系统，以及自主研发微变形测量系统。试验土料采用南京地铁穿越的典型土层-粉质黏土的重塑土，试验固定参数：黏土含水率为30%，常应力法向边界条件，剪切速率为5 mm/min，最大剪切位移11 mm。开展3种接触面粗糙度（0.3、0.8、1.4 mm），3種界面层温度（-6、-10、-14 ℃）和4种法向应力（100、300、500、700 kPa）条件下冻黏土与结构界面层单调剪切试验。

1.1 冻土界面层弹塑性本构模型构建

当冻土作为一个界面黏结层时，冻土内部物理过程的变化基本类似，但是其对于结构与冻土间的相互影响就变得非常重要。由于冻土与结构两者之间的接触决定了两者间的稳定性，如果冻土界面层先于冻土本身发生破坏，则对于工程结构的安全性造成影响，甚至引起结构破坏。所以建立冻土界面层本构模型具有科学和工程意义。

可以认为，冻土界面层随着温度降低会由准脆性破坏向脆性破坏转化。因此，在冻土界面层本构模型的建立过程中，需要考虑温度、粗糙度和法向应力等因素的影响。

由图1可以看出，冻土与结构接触界面层之间剪切过程有3个发展阶段。

首先是冻土体与结构之间在法向应力作用下密合冻结阶段;在水平剪切力作用下，冻土界面层开裂膨胀阶段，进入第2发展阶段;冻土界面层在结构剪切作用下发生塑性损伤，并在法向应力作用开始沿剪切面滑动摩擦，进入第3发展阶段。

冻土界面层单调剪切试验[13]结果表明，冻土界面层剪切强度随着结构粗糙度的增加而提高，实验中将结构粗糙面规则化为锯齿状，因此，结合文献[14]，由图1可以得到：

τn=τcosi-σsiniσn=σcosi+τsini。（1）

假定锯齿面的滑动破裂服从库仑-纳维尔 （Coulomb-Navier）准则，并假定内聚力（C） 为 0，则

τn=σntanθ。 （2）

式中，θ为粗糙面的内摩擦角。

将公式（1）代入公式（2），冻土界面层滑动破坏准则：

τ=σtan（θ+i）。 （3）

公式（3）相当于图2中冻土界面层沿锯齿面膨胀阶段，当法向应力σ较大时，结构面板将剪断冻土界面层，并沿该面作摩擦剪切，其剪断准则为：

τ=C+σtanθ。 （4）

通过冻土界面层单剪实验结果[13]分析发现，在不同法向应力作用下的冻土界面层剪切破坏，冻土界面层力学特性对法向应力有非常明显依赖行为。这一点是以往的研究中没有详细阐述的一个现象，且这种法向应力敏感程度还依赖于冻土界面层温度与含水率。为了能够描述这样的塑性行为，提出对于经典摩尔-库仑准则进行修正的塑性本构模型。基于细观维象的考虑，发现冰晶体与其包裹的土颗粒所组成的冻土界面层结构需要考虑能够反映围压的应力不变量。

传统的摩尔-库仑塑性屈服准则（考虑应变强化）表示为：

F=τn-μσn-c≤0。 （5）

式中：c为冻黏土黏聚力;μ为界面摩擦系数。

依据文献[15]，对其进行扩充，引入第一应力不变量I1，根据摩尔-库仑准则得到

F=αI1+τn–μI1σn-c≤0。（6）

式中：α为一个冻土界面层参数，受结构粗糙度影响;μ（I1）表示摩擦系数是第一应力不变量的函数，表征冻土界面层的特性;c为与界面层温度相关的冻土黏聚力。

1.2 冻土界面层弹塑性损伤分析

1.2.1 建模理论基础

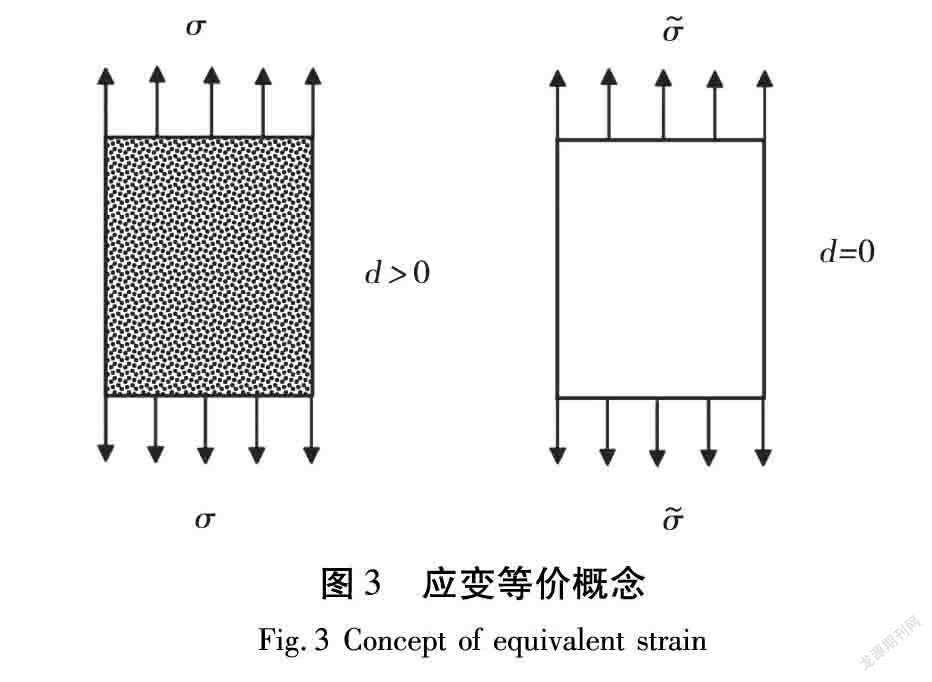
（1）应变等价原理

应力（σ）作用在受损材料上引起的应变与有效应力（σ～）作用在无损材料上引起的应变等价，如图3所示。

εij=σijE～ijkl=σ～ijEijkl=σij（1-d）Eijkl。（7）

式中：Eijkl为无损材料弹性模量;σij为平面应力;d为损伤因子 ;ij为平面应变 ;σ～ij为平面有效应力。

公式（7）表示一维问题中受损材料的本构关系。

将公式（7）改写为：

εkl=σijE～ijkl。（8）

式中受损材料有效弹性模量E～ijkl=Eijkl（1-d）。

由此得到

d=1-E～ijklEijkl。 （9）

（2）能量等效原理

西多霍夫（Sidoroff）认为用柯西应力和含损伤模量表示的弹性能等于用有效应力和初始无损模量表示的弹性能[16]。在一维情况下：

ρψe=12εeijσij=12σ2ijE～ijkl=12σ～2ijEijkl 。（10）

式中，Ψe为弹性应变能。

同时σ～ij=σij1-d故有

σ2ijE～ijkl=σ2ijEijkl（1-d）。（11）

从而得到

E～ijkl=（1-d）2Eijkl。 （12）

因此能量等效原理得到的弹性模量与损伤的关系，再由应变等效假设得到：

ε～ij=σ～klEijkl=σklEijkl（1-d）=（1-d）σklEijkl（1-d）2=（1-d）εij。 （13）

当采用弹塑性损伤理论描述冻土界面层行为时，利用等效应变假设可以得到含损伤的控制方程如下：

σ=（1-d）Del0/（ε-εpl）-Del（ε-εpl）。（14）

式中 ：Del0为无损时材料刚度;Del为损伤时材料刚度;σ为Cauchy应力;ε为总应变量;εpl为塑性应变量。

同时根据连续损伤力学概念可以定义有效应力表达式为：

σ～=Del0/（ε-εpl）。（15）

式中，σ～为有效应力。

有效应力与cauchy应力之间的关系为：

σ=（1-d）σ～。 （16）

根据参考文献[15]，为了区分冻土界面层类材料拉伸与压缩行为的不同，使用2个强化变量ε～plt和ε～plc，分别表示拉伸等效塑性应变和壓缩等效塑性应变，强化变量的演化方程可以表示为：

ε～pl=ε～pltε～plc;ε～·pl=h（σ～，ε～pl）·ε·pl。（17）

式中：ε～pl为等效塑性应变向量;h（σ～，ε～pl）为强化函数。

1.2.2 界面层弹塑性损伤分析

冻土界面层剪切应力-剪位移曲线反映界面层剪切破坏过程，从损伤角度来看，冻土界面层的破坏过程，就是其损伤形成和扩展累积直至完全损伤的过程。从冻土界面层的剪切应力-剪位移典型曲线（图4）可看出，冻土界面层从承载到破坏的损伤过程[17-27]可分为初始损伤阶段、脆弹性损伤阶段、损伤发展阶段、应力峰值点损伤、损伤快速持续累积阶段、损伤平缓持续累积阶段和摩擦强度残余阶段。

在初始损伤阶段（O点），冻土界面层试样存在表面及内部微裂纹或微空隙的初始损伤，冻土界面层剪切试验的剪切应力-剪位移曲线应以初始损伤d0为出发点。

脆弹性损伤阶段（OA段），冻土界面层的剪切应力-剪位移曲线开始斜直线上升段，损伤值与初始损伤值d0相差不大，脆弹性损伤是可恢复。从图4可以看出这一阶段的上界点约为峰值应力τf的30%～40%。

损伤发展阶段（AB段），冻土界面层的剪切应力-剪位移曲线的斜率不断变化，形成上升曲线段，表明这一阶段的冻土界面层的承载力在增大，但在冻土界面层内出现新的不可恢复的损伤，即已经含有不可恢复的弹塑性损伤，这一阶段的损伤大于初始损伤。

剪切应力峰值点损伤（B点），当冻土界面层内在荷载作用下损伤持续发展，因为有效承载面积的减小，其抗剪强度由逐渐增加变为逐渐减小，临界点是冻土界面层的峰值剪应力τf，对应达到峰值损伤df，说明冻土界面层损伤有了一定程度的积累。

损伤快速持续累积阶段（BC段），从图4可见，峰值应力过后，剪切应力-剪位移曲线迅速呈现凹形下降段，表明冻土界面层的剪切应力在下降，而剪位移仍然在增加，出现冻土界面层的应变软化特性。随着冻土界面层的损伤发展到一定的程度时，剪切应力在逐渐下降;按照损伤理论，剪切应力-剪位移曲线下降段的剪切应力实际上是名义剪切应力τ，而有效剪切应力τ～仍在增加，产生不可恢复的塑性损伤，下降段的前半段比较快，这一阶段剪切应力下降约τf/3处。

损伤平缓持续累积阶段（CE段），曲线下降段的后半段剪切应力下降平缓，损伤发展平缓。

极限损伤（即摩擦强度残余阶段ED段），冻土界面层的剪切应力-剪位移曲线平直段，剪切应力由于摩擦作用而保持一个平缓的定值。按损伤理论，对应极限损伤dc=1。

图5中折线OAB表示冻土界面层仅有初始损伤的剪切作用，为理想弹塑性曲线，而实际剪切试验冻土界面层发生损伤和损伤累积，在剪切应力-剪位移曲线上表现为上升段的非线性段和下降段的凹形曲线，出现应变软化现象。当假设冻土界面层为理想无损材料时，其剪切应力-剪位移曲线见图5中折线OA′B′。从图5看出，理想冻土材料的无损弹性模量（OA′的斜率）要大于含有损伤的弹性模量（OA的斜率）。同时，理想无损冻土界面层的峰值应力τ′f也大于含有初始损伤的冻土界面层的峰值应力τf。

通过分析可见，冻土界面层剪切过程就是包含初始损伤的损伤累积直至破坏的过程。

1.3 冻土界面层弹塑性损伤模型

冻土界面层剪切过程分别经历弹性阶段和塑性损伤阶段，最后进入残余强度摩擦阶段。从能量观点来分析，外力做功转化能量可分为弹性、塑性和损伤3个部分。运用能量守恒定律来推导材料的本构，具有不用考虑相关参数的矢量合成优势，只需要将相关部分能量加减处理。热力学第一定律描述热力学过程中能量守恒，而热力学过程进行的方向问题在热力学第二定律做了相应规定[28]。

由热力学第一定律可以推导得到方程：

ρe·=ρε·-qk.k+ρr·。（18）

式中：e为内能;q为热源。

又根据热力学第二定律的卡拉西奥多里（Caratheodory）解释系统的总熵增量表达式可以表述为：

dS=dSr+dSi，dSi≥0。  （19）

其中，dSr和dSi分别为系统供给的熵增量和系统内部耗散产生的熵增量。将其用率形式表示为：

S·r=dSrdt=∫Vρr·-（qkT），kdVS·i=∫Vρσ*dV=∫Vρs·idV。（20）

其中s·i=*。

将公式（20）代入公式（19）得到：

∫Vρ*dV=∫Vρs·dV-∫V[ρr·T-（qkT），]dV。（21）

由于体积任意性得到：

σ*=s·-r·T+1ρ（qkT）≥0 。（22）

根据热力学第二定律可知σ*≥0，并且有qk，k=T（qkT），k-Tqk（1T），k，同时得到了克劳修斯-杜亨（Clausius-Duhem）不等式.

ρT*=ρ（Ω·+Ts·-e·）-1TT，kqk≥0。（23）

对于存在耗散机制，可以得到应变能表达式的Clausius-Duhem表达式可以表达为：

ρTs·≥ρe·（s，εij，ξi）-σijε·ij。（24）

其中e·包含的内变量包括熵、应变和耗散内变量（分别为s，εij，ξi）。将e·展开得到

ρTs·≥ρe·ss·+ρe·εijε·ij+ρe·ξiξ·i-σijε·ij。（25）

整理得到

ρ（T-e·s）s·+（σij-ρe·εij）ε·ij-ρe·ξiξ·i≥0。（26）

如果是一个不存在耗散的可逆过程，其中代表耗散的内变量ξ·i=0，并且ρTs·=0。根据正交法则进而得到功共轭的关系式为：

T=e·s，σij=ρe·εij 。（27）

对应耗散项的功共轭率形式为：

Y=ρe·ξiξ·i。 （28）

定义应变自由能和应力自由能分别为：

（εij，T，ξi）=e-Ts。（29）

（σij，T，ξi）=σijεij-（εij，T，ξi）。（30）

那么利用应变能和应力能表达式的Clausius-Duhem不等式可以表示为：

Y=（σij-ρεij）ε·ij-ρ（s+T）T·-ρξiξ·i≥0Y=（σij）σ·ij+ρ（T-s）T·+ρξiξ·i≥0。

（31）

最终得到本构关系如下：

σij=ρεij，s=-T，Yi=-ρξiεij=ρσij，s=T，Yi=ρξi。（32）

在冻土界面层剪切试验过程中温度保持不变，即温度为常数，则T·=0。同时认为耗散是由于塑性和损伤导致的，即ξ1=εijp，ξ2=d就可以将公式（32）写成：

σ·ij=ρ2εijεklε·ij+ρ2εijεpijε·pij+ρ2εijdd·=

σ·eij+σ·pij+σ·dij

ε·ij=ρ2σijσijσ·ij+ρ2σijεpijε·pij+ρ2σijdd·=

ε·eij+ε·pij+ε·dij。（33）

公式（33）中将应力率和应变率分别拆分为弹性、塑性和损伤3个部分。接下来定义比体积应变自由能和比体积应力自由能为：

ρ=w（εij，εpij，d）=12（εij-εpij）Eijkl（d）（εkl-εpkl）

ρ=w（σij，d）=12σijLijkl（d）σkl。 （34）

并且得到功共轭的耗散项表达式为：

Yp=σij=Eijkl（d）（εkl-εpkl）

Yd=12（εij-εpij）Eijkl（d）d（εkl-εpkl）。（35）

其中，Lijkl（d） = （Eijkl（d））-1為考虑损伤的弹性柔度张量。耗散率为：

Y=σijεpij+Ydd。 （36）

这样塑性行为和损伤行为的求解归结为两个屈服函数（势能函数）的定义，即

Fp=Fp（σij，d，c0，θ0）≤0。  （37）

其中c0，θ0和Fp分别代表了冻土界面层初始抗剪强度、初始内摩擦角和塑性屈服条件。根据已提出的塑性屈服势公式（6），就可以得到新的屈服条件。

Fp=αI～1+τ～n-μ（I～1）σn-c≤0。（38）

式中：α是一个冻土界面层参数，受结构粗糙度影响;μ（I～1）表示摩擦系数是第一应力不变量的函数，表征冻土界面层的特性;c为冻土粘聚力，跟冻土界面层温度有关。

公式（38）上标～表示含损伤。用损伤共轭力Y表示的损伤条件为：

Fd=Fd（Y，εpij）≤0。 （39）

其中，Fd代表了损伤势能函数，继而可以得到损伤率的表达式为：

d·=λ·dFdY。  （40）

其中，λ·d为率形式的损伤乘子，其可以和率形式的塑性乘子根据一致性条件来迭代求解。

针对于冻土界面层，本文提出一个损伤势能函数，其表达式为：

Fd=（Yβ）m（1-d）2。   （41）

其中，Y的表达式为：

Y=12（1-d）2Eijklεijεkl。  （42）

2 模型验证

基于ABAQUS软件的二次开发功能，实现了自定义的弹塑性损伤本构模型的二次开发，并建立了基于冻土界面层剪切试验的有限元模型。采用位移-损伤和能量-损伤2种模式定义冻土界面层的弹塑性损伤模型，其中在竖向应力较高的2种工况下采用位移-损伤方法来定义冻土界面层本构。

冻土界面层塑性损伤本构模型涉及5个材料参数，分别为α、μ、c、m、β，其中，α代表法向应力相关的系数;μ为界面摩擦系数;c为冻土黏聚力;m表征断裂能参数;β为损伤参数。

参数μ通过冻土与结构接触界面直剪试验稳定剪切阶段试验数据计算而得到，c依据冻黏土直剪试验得到，参数α、m、β根据冻土界面层直剪试验数据反分析得到。接触界面层损伤模型参数见表1。

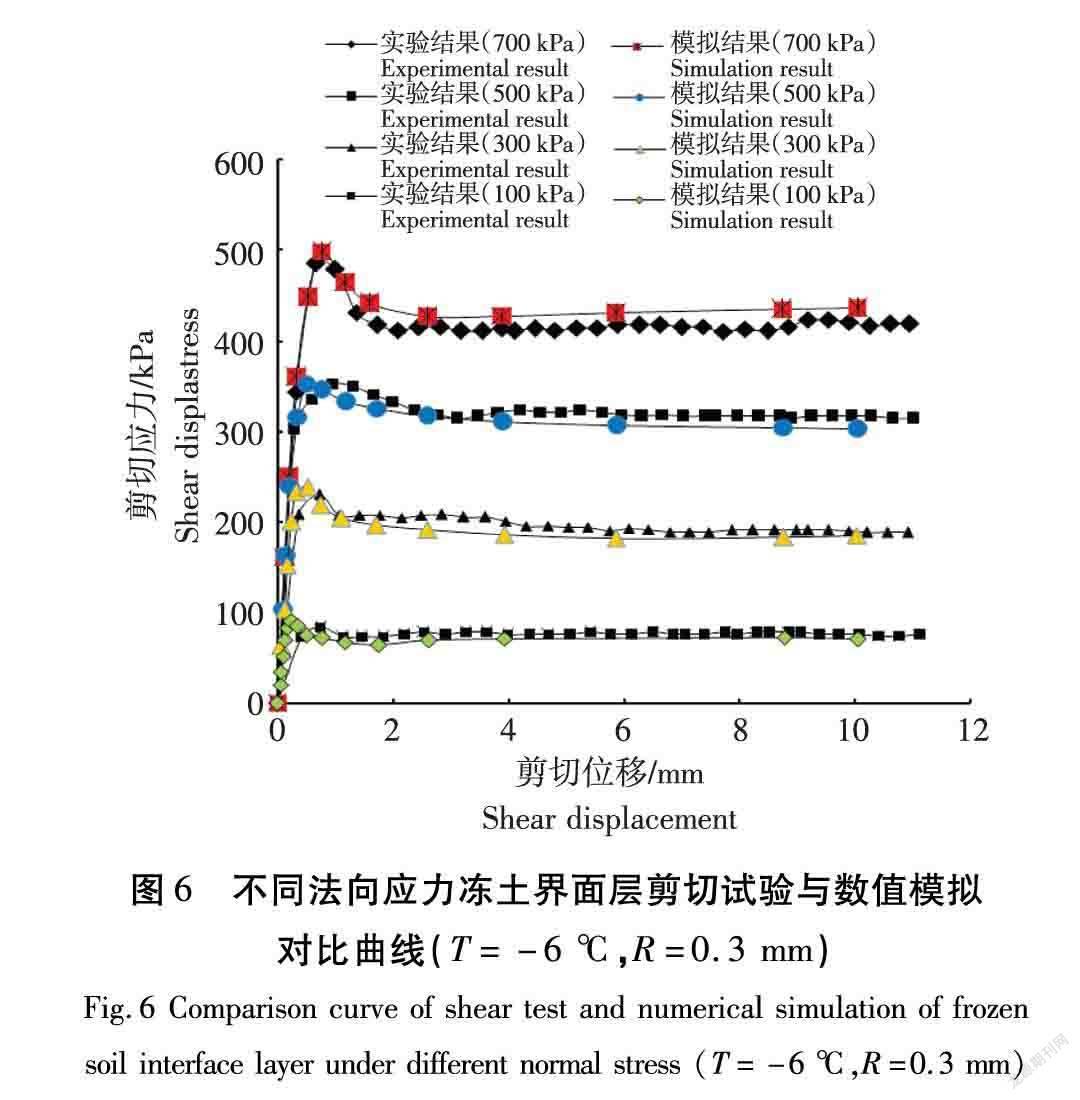
图6为冻土温度T=-6 ℃，结构粗糙度R=0.3 mm时，不同法向应力情况下的剪切应力-剪切位移曲线模拟结果与试验结果的对比。

由图6数值模拟曲线可见，不同法向应力条件下，随着相对剪位移增大，冻土界面层剪切应力上升，达到峰值剪切应力，而后衰减到稳定剪切应力。数值模拟曲线可再现冻土界面层这一剪切力学行为。在法向应力500、700 kPa情况下，两者弹性状态拟合较好，在模拟峰值剪切应力后衰减拐点位置与试验结果比较接近，说明位移-损伤法对于定义冻土界面的剪切力学行为存在一定优势。在法向应力100、300 kPa情况下，采用能量-损伤法定义损伤的演化，其试验曲线和模拟曲线拟合程度较高，说明采用能量方法来模拟较低法向应力冻土界面层的损伤剪切行为比较适合。从图6可见，数值模拟的力学特性同物理实验基本吻合。

3种温度冻土与0.3 mm粗糙度结构界面层，在法向荷载500 kPa条件下的剪切应力-剪切位移曲线模拟结果如图7所示。

由图7可见，随着冻土界面层温度降低，冻土界面层峰值剪切应力在增加，而在稳定剪切阶段时，接触界面层剪切应力受温度影响较小。这一规律同物理实验一致。主要原因为，初始剪切时冻土界面层需要克服接触界面冻结力和摩擦力，而稳定剪切阶段剪切应力主要是克服冻土界面层摩擦力，受温度影响较小，法向应力起决定作用。通过数值模拟可以发现，利用冻土界面层弹塑性损伤模型可很好地再现上述力学行为。

-10 ℃冻黏土与3种粗糙度结构接触界面层，在法向荷载500 kPa条件下，单调剪切剪应力与剪位移曲线模拟结果如图8所示。

由图8可见，随着粗糙度增加，冻土界面层峰值剪切应力在增加，在稳定剪切阶段，结构粗糙度对剪切应力影响较小。究其原因为：初始剪切时，当粗糙度变大，剪切模型中接触面积在增大，导致峰值剪切应力增大;在稳定剪切时，主要是冻土界面层内冻土体的摩擦力。这一数值模拟规律同物理模型实验一致，从而验证数值模型的有效性。

3 结论

基于冻土界面层的受力行为和破坏模式，推导了一个可以描述冻土界面层破坏行为的弹塑性损伤本构模型。主要结论如下。

（1）总结接触界面层冻土体材料塑性和损伤基本理论，分析冻土界面层的剪切破坏特征，建立冻土界面层理论模型。

（2）基于经典的摩尔库仑准则，将内聚力与摩擦系数作为一个与应力第一不变量相关的函数，根据热力学第二定律和正交法则，构建了冻土界面层弹塑性损伤模型，能够描述冻土界面层在剪切峰值过后的塑性摩擦行为与竖向围压关系。

（3）基于ABAQUS软件的二次开发功能，实现了自定义的弹塑性损伤本构模型的二次开发，并建立了基于冻土界面层剪切试验的有限元模型。将计算结果与试验进行对比，两者间具有一致性，从而验证了模型的有效性。

【参 考 文 献】

[1]GHABOUSSI J， WILSON E L， ISENBERG J. Finite element for rock joints and interfaces[J]. Journal of the Soil Mechanics and Foundations Division， 1973， 99（10）： 833-848.

[2]DESAI C S， MA Y Z. Modelling of joints and interfaces using the disturbed-state concept[J]. International Journal for Numerical and Analytical Methods in Geomechanics， 1992， 16（9）： 623-653.

[3]CLOUGH G W， DUNCAN J M. Finite element analyses of retaining wall behavior[J]. Journal of the Soil Mechanics and Foundations Division， 1971， 97（12）： 1657-1673.

[4]BRANDT J R T. Behavior of soil-concrete interface[D]. Edmonton： University of Alberta， 1985.

[5]MORTARA G， FERRARA D， FOTIA G. Simple model for the cyclic behavior of smooth sand-steel interfaces[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2010， 136（7）： 1004-1009.

[6]DESAI C S， ZAMAN M M. Thin layer element for interfaces and joints[J].International Journal for Numerical & Analytical Methods in Geomechanics， 1984， 8（1）：19-43.

[7]陳慧远.摩擦接触单元及其分析方法[J].水利学报，1985，16（4）：44-50.

CHEN H Y. Friction contact surface element and its analysis method[J]. Journal of Hydraulic Engineering， 1985， 16（4）： 44-50.

[8]钱家欢.接触面剪切流变特性试验研究[C]//安关峰，高大钊，岩土与水工建筑物共同作用研究成果汇编.南京：河海大学，1990.

QIAN J H. Experimental study on shear rheological properties of contact surface[C]//AN G F， GAO D Z. Compilation of research results on interaction between geotechnical and hydraulic structures. Nanjing： Hohai University， 1990.

[9]卢廷浩，鲍伏波.接触面薄层单元耦合本构模型[J].水利学报，2000，31（2）：71-75.

LU T H， BAO F B. A coupled constitutive model for interface thin layer element[J]. Journal of Hydraulic Engineering， 2000， 31（2）： 71-75.

[10]HU L M， PU J L. Testing and modeling of soil-structure interface[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2004， 130（8）： 851-860.

[11]张嘎，张建民.粗粒土与结构接触面三维本构关系及数值模型[J].岩土力学，2007，28（2）：288-292.

ZHANG G， ZHANG J M. Three-dimensional model of interface between structure and coarse grained soil[J]. Rock and Soil Mechanics， 2007， 28（2）： 288-292.

[12]孙厚超，杨平，王国良.冻土与结构接触界面层力学试验系统研制及应用[J].岩土力学，2014，35（12）：3636-3641，3643.

SUN H C， YANG P， WANG G L. Development of mechanical experimental system for interface layer between frozen soil and structure and its application[J]. Rock and Soil Mechanics， 2014， 35（12）： 3636-3641， 3643.

[13]孙厚超，杨平，王国良.冻黏土与结构接触界面層单剪力学特性试验[J].农业工程学报，2015，31（9）：57-62

SUN H C， YANG P， WANG G L. Monotonic shear mechanical characteristics and affecting factors of interface layers between frozen soil and structure[J]. Transactions of the Chinese Society of Agricultural Engineering， 2015， 31（9）： 57-62.

[14] 陆家佑.岩体力学及工程应用[M].北京：中国水利水电出版社，2011.

LU J Y. Rock mechanics and its engineering application[M]. Beijing： China Water & Power Press， 2011.

[15]曹鹏，冯德成，沈新普，等.基于ABAQUS平台的塑性损伤子程序开发及其稳定性研究[J].工程力学，2012，29（S2）：101-106.

CAO P， FENG D C， SHEN X P， et al. Development of plasticity-damage model based on Abaqus and algorithm stability analysis[J]. Engineering Mechanics， 2012， 29（S2）： 101-106.

[16]李兆霞.损伤力学及其应用[M].北京：科学出版社，2002.

LI Z X. Damage mechanics and application[M]. Beijing： Science Press， 2002.

[17]LAI Y M， WU Z W， ZHU Y L， et al. Elastic visco-plastic analysis for earthquake response of tunnels in cold regions[J]. Cold Regions Science and Technology， 2000， 31（3）： 175-188.

[18]凌贤长，徐学燕，徐春华，等.冻结哈尔滨粉质黏土超声波速测定试验研究[J].岩土工程学报，2002，24（4）：456-459.

LING X Z， XU X Y， XU C H， et al. Study on frozen Harbin silty clay through its measuring tests of ultrasonic velocity[J]. Chinese Journal of Geotechnical Engineering， 2002， 24（4）： 456-459.

[19]LING X Z， XU X Y， QIU M G， et al. Ultrasonic experiment study on dynamic elastic mechanical indexes of frozen silty clay[C]//Proceedings of the 5th International Symposium on Permafrost Engineering， 2002：38-42.

[20]徐春华，徐学燕，邱明国，等.循环荷载下冻土的动阻尼比试验研究[J].哈尔滨建筑大学学报，2002，35（6）：22-25.

XU C H， XU X Y， QIU M G， et al. Experimental study on dynamic damping ratio of frozen soil under cyclic loading[J]. Journal of Harbin University of Civil Engineering and Architecture， 2002， 35（6）： 22-25.

[21]LI X Z， XU X Y， XU C H. The influence on ground seismic hazard of frozen soil shear-wave velocity[C]//In： Proceedings of the 5th International Symposium on Permafrost Engineering， 2002：43-47.

[22]石泉彬，杨平，王国良.人工冻结砂土与结构接触面冻结强度试验研究[J].岩石力学与工程学报，2016，35（10）：2142-2151.

SHI Q B， YANG P， WANG G L. Experimental study on adfreezing strength of the interface between artificial frozen sand and structure[J]. Chinese Journal of Rock Mechanics and Engineering， 2016， 35（10）： 2142-2151.

[23]石泉彬，杨平，于可，等.冻土与结构接触面次峰值冻结强度试验研究[J].岩土力学，2018，39（6）：2025-2034.

SHI Q B， YANG P， YU K， et al. Sub peak adfreezing strength at the interface between frozen soil and structures[J]. Rock and Soil Mechanics， 2018， 39（6）： 2025-2034.

[24]石泉彬， 杨平， 谈金忠， 等. 冻土与结构接触面冻结强度压桩法测定系统研制及试验研究[J]. 岩土工程学报， 2019， 41（1）： 139-147.

SHI Q B， YANG P， TAN J Z， et al. Development of measuring system by pile-pressing method and experimental study on adfreezing strength at interface between frozen soil and structure[J]. Chinese Journal of Geotechnical Engineering， 2019， 41（1）： 139-147.

[25]何鵬飞，马巍，穆彦虎，等.冻土-混凝土界面冻结强度特征与形成机理研究[J].农业工程学报，2018，34（23）：127-133.

HE P F， MA W， MU Y H， et al. Study on freezing strength characteristics and formation mechanism of frozen soil-concrete interface[J]. Transactions of the Chinese Society of Agricultural Engineering， 2018， 34（23）： 127-133.

[26]何鹏飞，马巍，穆彦虎，等.冻融循环对冻土–混凝土界面冻结强度影响的试验研究[J].岩土工程学报，2020，42（2）：299-307.

HE P F， MA W， MU Y H， et al. Experiment study on effects of freeze-thaw cycles on adfreezing strength at frozen soil-concrete interface[J]. Chinese Journal of Geotechnical Engineering， 2020， 42（2）： 299-307.

[27]王兰民，张冬丽，吴志坚，等.地温对冻土动力特性及其场地地震动参数的影响[J].中国地震，2003，19（3）：195-205.

WANG L M， ZHANG D L， WU Z J， et al. The influence of earth temperature on dynamic characteristics of frozen soil and the parameters of ground motion on the sites of frozen soil[J]. Earthquake Research in China， 2003， 19（3）： 195-205.

[28]张峰瑞，姜谙男，江宗斌，等.低温冻土地区的软土路基蠕变沉降数值分析[J].公路工程，2020，45（4）：79-84.

ZHANG F R， JIANG A N， JIANG Z B， et al. Numerical analysis of creep settlement of soft soil subgrade in cryogenic frozen soil zone[J]. Highway Engineering， 2020， 45（4）： 79-84.

[29]朱兆荣，赵守全，韩侃，等.寒区高速公路路基填料冻胀特性的试验装置及方法[J].公路工程，2020，45（1）：156-162.

ZHU Z R， ZHAO S Q， HAN K， et al. Test device and method for frost heave characteristics of subgrade filling of freeway in cold regions[J]. Highway Engineering， 2020， 45（1）： 156-162.

[30]黄筑平.连续介质力学基础[M].2版.北京：高等教育出版社，2012.

HUANG Z P. Fundamentals of continuum mechanics[M]. 2nd Edition. Beijing： Higher Education Press， 2012.