桦木波动干燥过程中温度和水分扩散数值模拟

姜新波 宋靖 夏鹏

摘 要：为对木材干燥过程中温度和含水率这2个参数进行分析，本文应用开源软件OpenFOAM进行理论建模，修改simple求解器，自定义边界条件;对比桦木干燥过程中温度和含水率的实验数据，验证所建立模型的准确性;依据所建立模型的分析结果，对厚为50～80 mm、初始含水率为25%的桦木板材的波动干燥工艺进行分析和对比，并针对厚为70 mm的桦木板材的波动干燥工艺进行优化。结果表明，所建立模型的数值计算结果与实验数据的平均误差均控制在5%以内;干燥过程中，随着相应桦木板层厚度的增加，板材含水率梯度模的大小呈递减趋势;对于厚为70 mm、初始含水率为25%的桦木板材適当提升波动干燥冷却阶段的温度，可以优化干燥工艺。

关键词：开源软件OpenFOAM;波动干燥;水分扩散;数值模拟;工艺优化

中图分类号：S782.31    文献标识码：A   文章编号：1006-8023（2022）01-0034-08

Numerical Simulation of Temperature and Moisture Diffusion

during Wave Drying of Birch

JIANG Xinbo， SONG Jing， XIA Peng*

（Forestry Machinery and Woodworking Engineering Technology Center， Northeast Forestry University， Harbin 150040， China）

Abstract：For the analysis of the two parameters of temperature and moisture content in the process of wood drying， this paper used the open source software OpenFOAM for theoretical modeling， modified the simple solver and defined the boundary conditions. The accuracy of the model was verified by comparing the experimental data of temperature and moisture content during birch drying. According to the analysis results of the established model， the fluctuating drying process of birch plate with thickness of 50 - 80 mm and initial moisture content of 25% was analyzed and compared， and the fluctuating drying process of birch plate with thickness of 70 mm was optimized. The results showed that the average error between the numerical results of the model and the experimental data was controlled within 5%. During the drying process， with the increase of the thickness of the corresponding birch wood layer， the size of the moisture content gradient mold decreased. For birch board with thickness of 70 mm and initial moisture content of 25%， appropriately increasing the temperature in the cooling stage of fluctuating drying can optimize the drying process.

Keywords：Open source software OpenFOAM; wave drying; moisture diffusion; numerical simulation; process optimization

0 引言

木材干燥是实木制品加工的重要工序，是保障和改善木材的品质、提高其利用率的重要环节[1]。木材干燥企业为了保证木材的干燥质量，一般都采取比较保守的干燥基准，从而造成了能源的浪费[2]，同时木材是高度异质性和各向异性的材料，对于同一树种，不同地区出产的木材，干燥特性也会不同。因此，每个树种都需要相应的干燥处理技术。周永东等[3-4]对50 mm厚辐射松锯材和25 mm厚桃花心木常规干燥工艺进行了优化干燥;付宗营等[5]以25 mm厚栓皮栎锯材为对象，研究制定合适的常规干燥工艺基准，并对锯材干燥中的各种指标进行评价;韦妍蔷等[6]采用过热蒸汽对马尾松锯材进行干燥处理，探讨处理条件对木材颜色、厚度、含水率偏差以及脱脂效果的影响;周凡等[7]采用百度试验法研究黑木相思木材的干燥特性，并制定25 mm厚黑木相思锯材的干燥基准。针对不同的木材需要制定不同的干燥基准，耗时多，材料成本巨大，这就体现出针对木材干燥过程的理论建模的重要性。He等[8]建立了木材样品真空干燥力的热质耦合传递模型; Li等[9]研究了预蒸柞木木材干燥过程中水分横向移动机制，并研究了厚为25.4 mm橡木在窑炉干燥过程中的干燥变形情况;周正等[10]建立了描述木材干燥过程含水率和温度变化的数学模型，并对含水率和温度的变化情况进行了仿真。

目前关于木材干燥研究集中于常规连续干燥，且干燥的板材厚度较小，而对于某些硬阔叶树材的厚板，在干燥过程中板材容易产生很大的含水率梯度，其干燥过程较为困难，为加快干燥速度，并且避免较大的含水率梯度，可采用波动式干燥基准。但目前波动干燥的相关研究较少，鉴于此，本文对桦木厚板的波动干燥展开仿真研究，对板材模型内可压缩水蒸气层流特性干燥过程进行三维数值模拟，并选取特定位置研究该截面的温度、湿度分布特点，并进一步研究不同参数对干燥结果影响。

1 传质传热模型和数值计算方法

1.1 模型构造

木材干燥是保障和改善木材品質、减少损失、提高利用率的重要途径。木材在干燥时内部水分状态可分为液态水和水蒸气，其中液态水可分为自由水和结合水，如图1所示。在木材干燥过程中，既存在木材表面与干燥介质之间的对流换热，也存在木材内部热传递，热量从木材的外表面传到内层，水分的运动方向与之相反[11]。

木材在干燥过程中水分有2种扩散类型[12]：水蒸气通过空气在细胞腔中的扩散（气体间扩散）和水在木材细胞壁中的扩散（束缚水扩散）。木材水分迁移形式主要包括基于压力差的毛细管中的渗流与基于浓度差的扩散[13]。

假设木材中的传质只发生在扩散过程中，求解传热传质耦合方程，建立模型。木材热处理过程中的三维热湿传递方程如公式（1）和公式（2）所示，建立一个三维非稳态多孔介质传热传质模型。该模型主要考虑温度和水分含量变化的情况[14-15]。

传热方程：

ρmCqt=SymbolQC@kqSymbolQC@T。（1）

传质方程：

Mt=SymbolQC@·DSymbolQC@M。（2）

式中：ρm为木材的密度，数值为660 kg /m3  ;Cq为比热容，数值为1 884 J/（kg· K）;SymbolQC@为Nabla算子; T为温度， K;kq为导热系数， W/（m·K），其中kq在3个方向的分量为kqz=2kqx=2kqy=0.18;M为含水率， %;D为扩散系数， m2 /s，数值由公式（5）计算得到。

含水率在纤维饱和点以上时，木材毛细管内的自由水靠毛细管弯液面的表面张力差而移动;含水率在纤维饱和点以下时，同时存在细胞壁内吸着水和细胞腔内水蒸气的移动，含水率梯度和质量浓度梯度是主要驱动力[16]。

扩散系数（D）[17]取决于温度和含水量，表示为低于纤维饱和点的瞬时木材含水量的函数。当木材含水量高于其在纤维饱和点处的值（Mfsp）时，扩散率为该值的函数。

D=f（M，T） M<Mfsp

f（Mfsp，T） M≥Mfsp。（3）

Mfsp=0.573 15-0.001T。（4）

D=0.94exp（2.07M）exp[-2 853/（T+273.15）]×10-5。（5）

在笛卡尔坐标系（Cartesian coordinates）中，公式（1）可写成

ρmCqt=x（kqx·x）+y（kqy·y）+

z（kqz·z）。（6）

为求解该方程，需要提出一些假设条件：

（1） 假设实验木材的结构、物理性质偏差较小。

（2） 导热系数仅随木材的含水率和温度变化。

传热方程木材内部单元的差分形式：

ρmCqΔxΔyΔzTn+1i，j，k-Tni，j，kΔτ=（kqxTn+1i-1，j，k-Tni，j，kΔx+

kqxTn+1i+1，j，k-Tni，j，kΔx）ΔyΔz+…+（kqyTni，j-1，k-Tni，j，kΔy+

kqyTni，j+1，k-Tni，j，kΔy）ΔxΔz+（kqzTni，j，k-1-Tni，j，kΔz+

kqzTni，j，k+1-Tni，j，kΔz）ΔxΔy。（7）

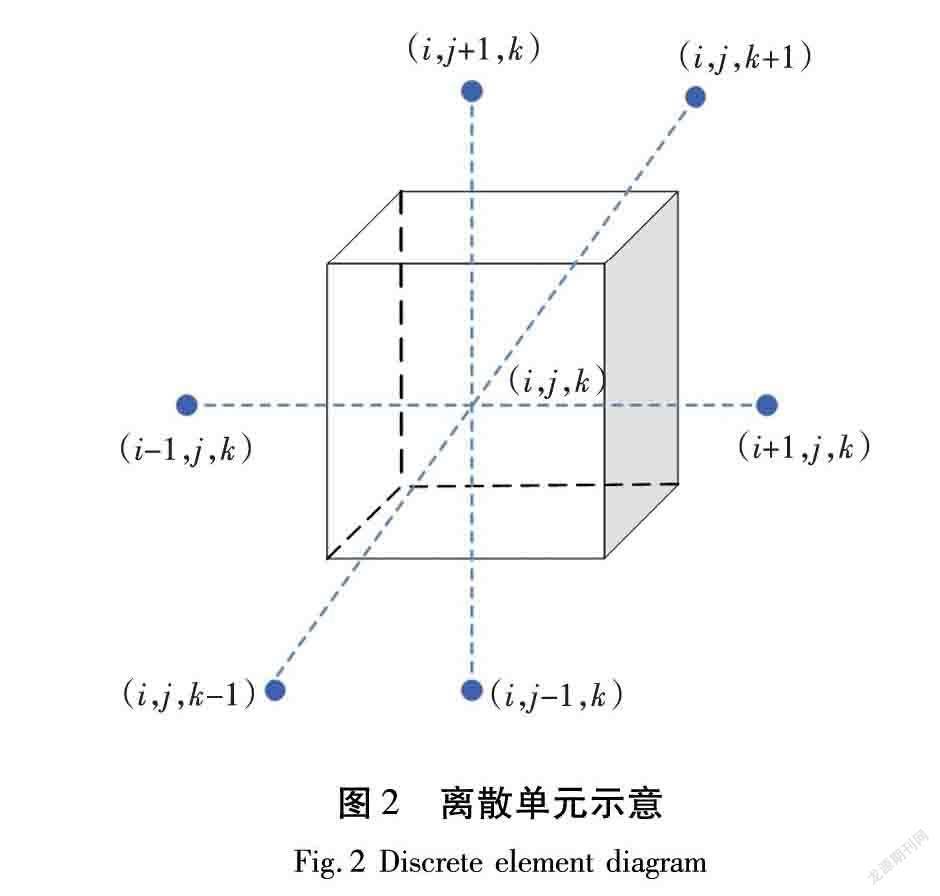
式中：i=2，3，…，I-1;j=2，3，…，J-1;k=2，3，…，K-1;Δx，Δy，Δz分别为3个方向的增量，离散单元的示意如图2所示。

传质方程在笛卡尔坐标系中可写成：

Mt=x（D·Mx）+y（D·My）+z（D·Mz）。（8）

求解该方程，假设条件为：

（1）忽略木材纤维纹理对扩散效果的影响，各方向的扩散系数相同。

（2）木材的含水率变化仅受扩散系数的影响。

传质方程木材内部单元的差分形式：

ΔxΔyΔzMn+1i，j，k-Mni，j，kΔτ=（DMn+1i-1，j，k-Mni，j，kΔx+

DMn+1i+1，j，k-Mni，j，kΔx）ΔyΔz+…+（DMni，j-1，k-Mni，j，kΔy+

DMni，j+1，k-Mni，j，kΔy）ΔxΔz+（DMni，j，k-1-Mni，j，kΔz+

DMni，j，k+1-Mni，j，kΔz）ΔxΔy。（9）

1.2 边界条件和初始条件

边界条件公式如下。

热传递：

-kqj=αq（T-Tg）+αmλ（M-Mg）。（10）

质量传递：

-DMj=αm（M-Mg）。（11）

式中：αq为对流换热系数，数值为15 W /（m2·K）;αm为对流传质系数，数值为1.6 × 10-5M/ s;Tg为环境温度， K;Mg为环境湿度， %，其值随工况变化。

初始条件如下。

传热方程：T=T0。（12）

传质方程：M=M0 。（13）

2 模型验证

2.1 几何建模

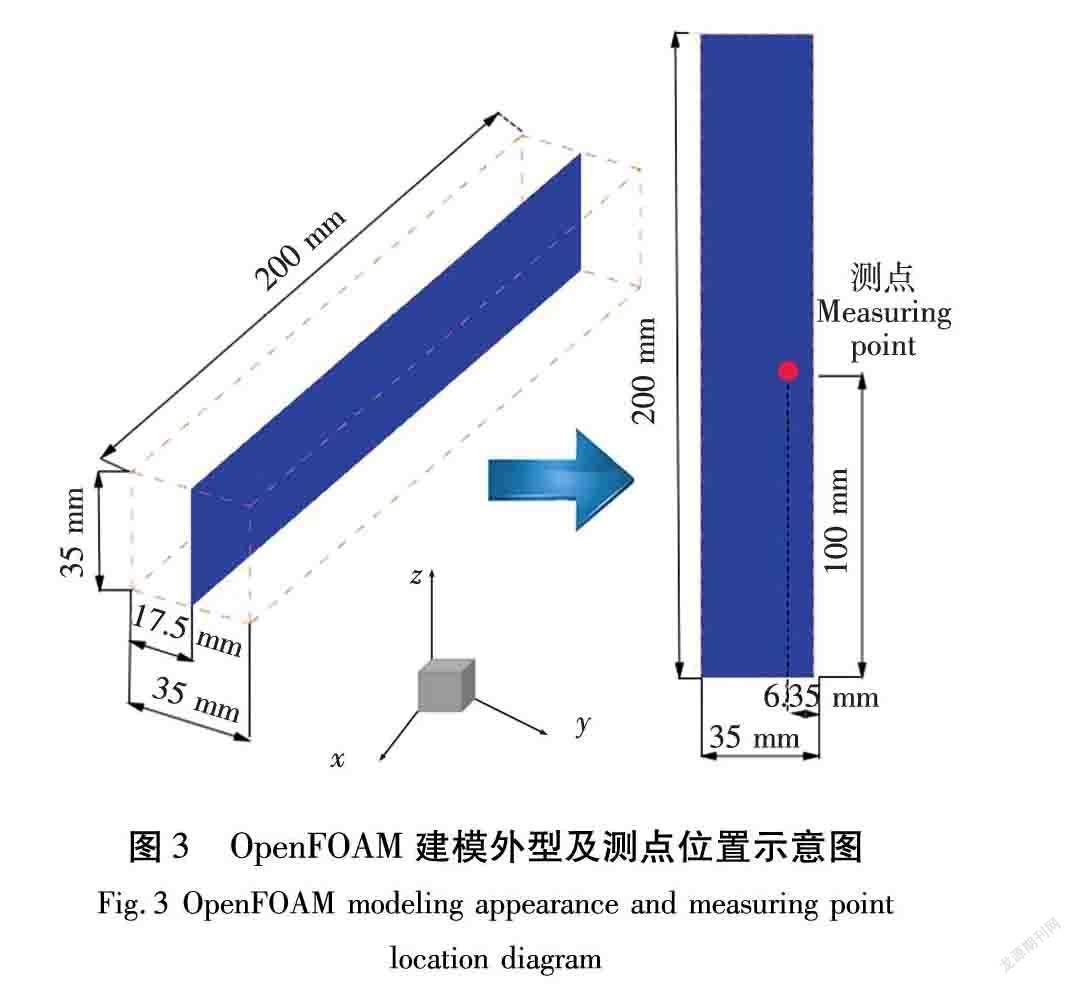
本文以文献[18]的实验数据为依据，以该实验所取木材尺寸进行建模仿真，木材的长200 mm、宽35 mm、高35 mm，数据采集的截面为木材长边所在的中间层，实验的含水率采用称重法得出，而仿真的平均含水率采用统计不同时刻木块所划分的每一个单元的含水率数据进行叠加取平均的方式，实验的温度数据测量位置在中间层位置，如图3所示。

2.2 网格划分

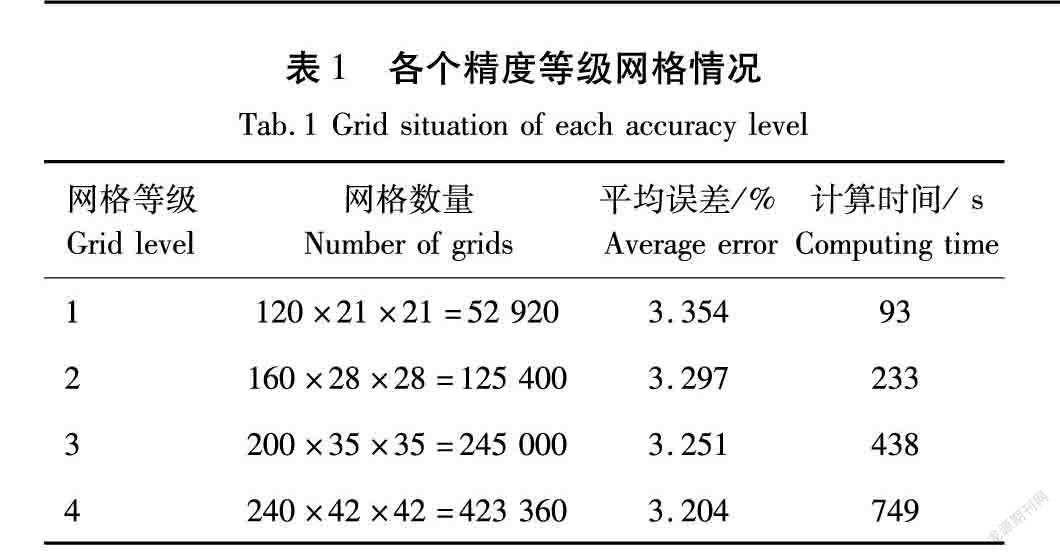
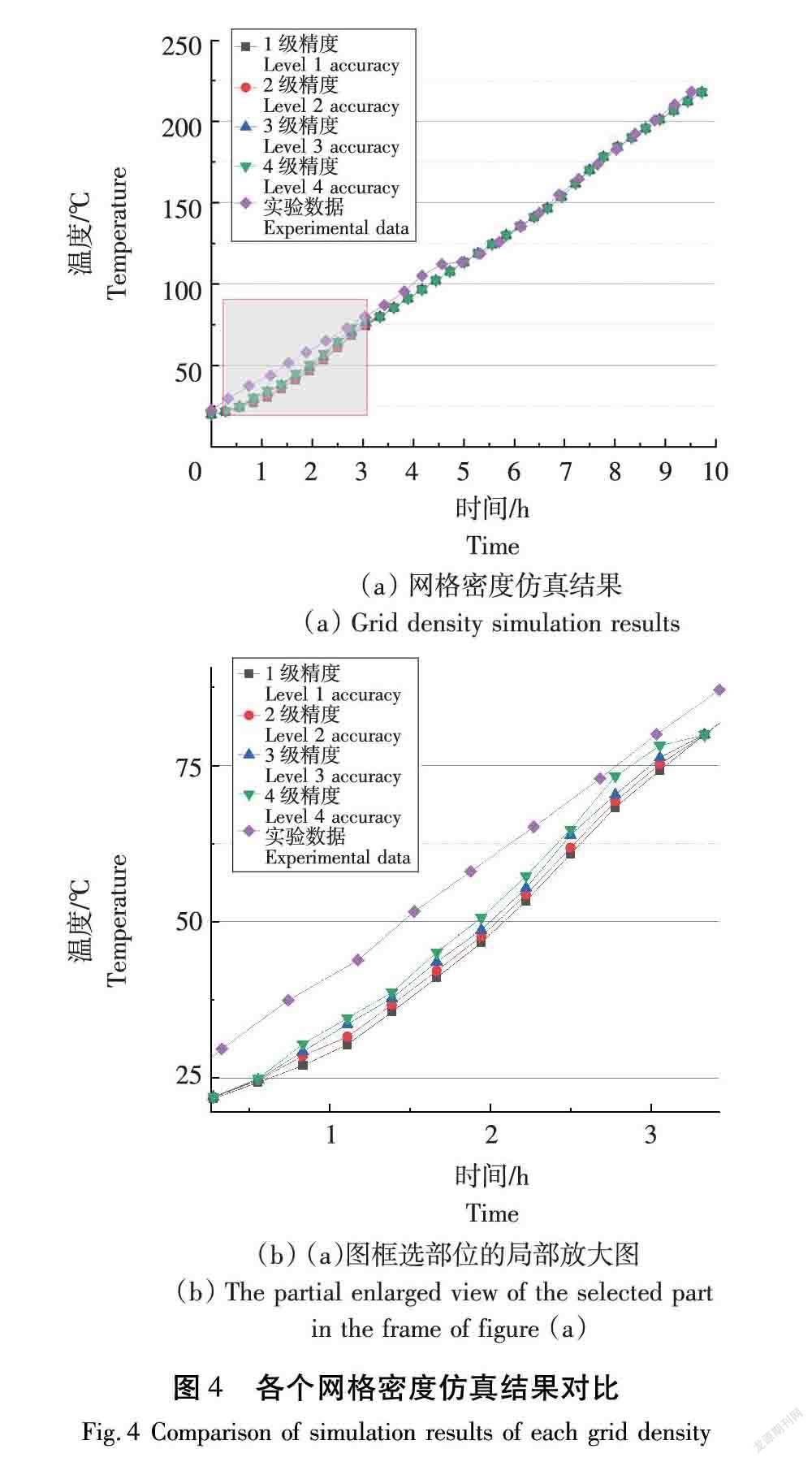
通过OpenFOAM中的blockMesh工具实现木材模型的划分，利用blockMesh工具生成1个35 mm×35 mm×200 mm的长方体模型。本模型网格划分采用结构网格，本文选取网格数为4个精度等级网格进行对比分析（表1），对比结果如图4所示。由图4可知，在满足工程上允许偏差范围的条件下，综合计算时间和误差大小以及实验中温度测试点所在位置，最终选取网格数为4级的网格进行后续的研究和分析。

2.3 数据对比

对比的文献中，实验采用密度为660 kg /m3的白桦木为实验材料，并在干燥前对尺寸为35 mm× 35 mm×200 mm的木材样品进行了热处理。 整个实验在惰性气体下进行，将干燥木材样品悬浮到管式炉中并采用天平实时记录样品质量变化，温度采集采用T型热电偶。

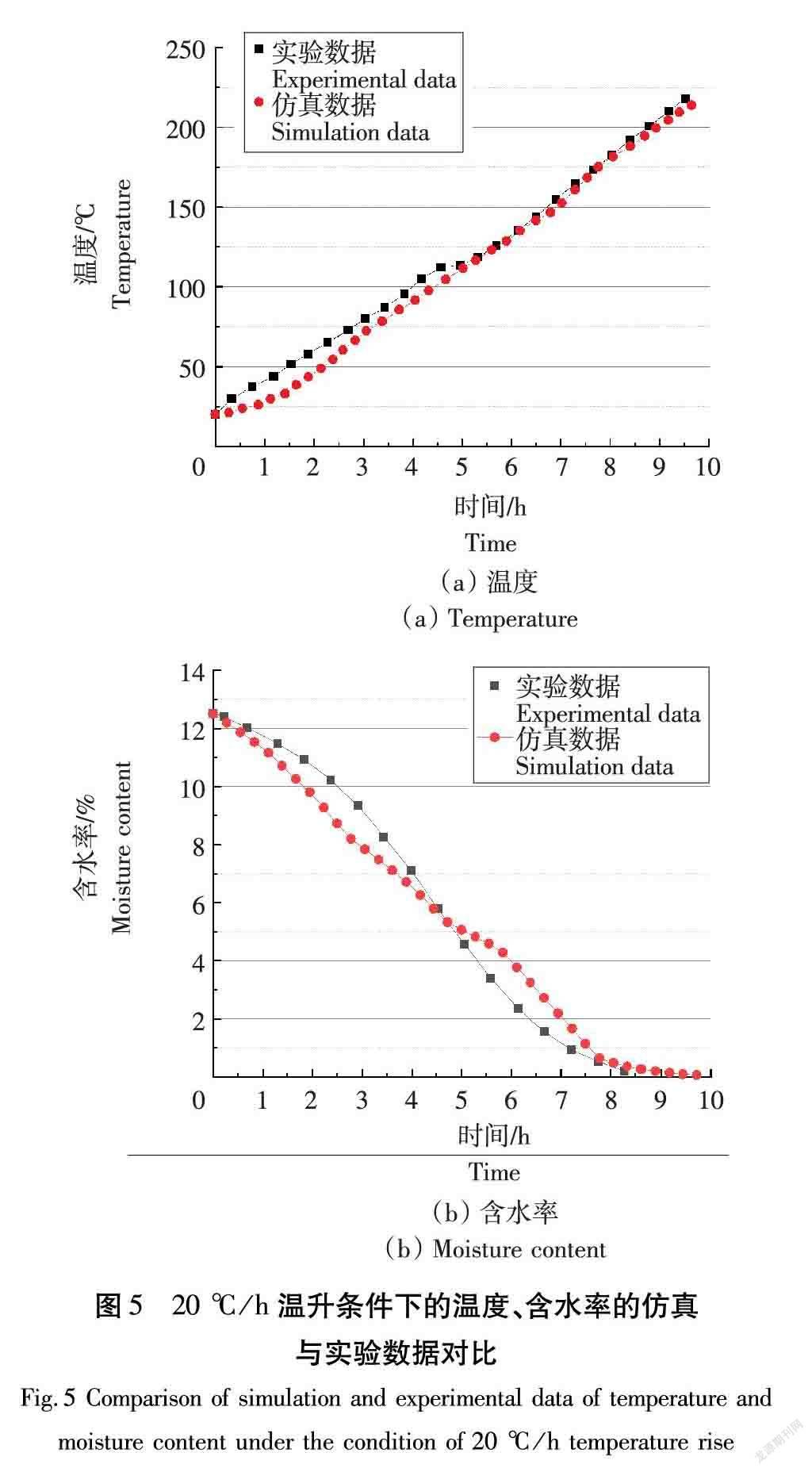
将测试位置处的温度和平均含水率变化的实验数据与本文模型的预测进行了比较，对比20 ℃/h温升条件下实验数据与模型预测的平均含水率和温度，并进一步给出了扩散模型预测的木材内的含水量和温度分布。

由图5可得，20 ℃温升条件下，在5 h之前的仿真效果不理想，主要原因在于模拟仿真温升固定，但实际实验过程中木材在进行实验前先预热半小时，使木材内部温度场呈现均匀分布的态势，仿真数据在温度110 ℃左右时出现大的数据偏差。图1（b）为平均含水率的仿真数据和实验数据的对比情况（12.5%），干燥前期和干燥末期的数据相关性较差，整体仿真数据在真实的实验数据之间徘徊，温度的平均误差为3.20%，含水率曲线的最大误差为9.87%，平均误差为4.909%，满足仿真精度要求。

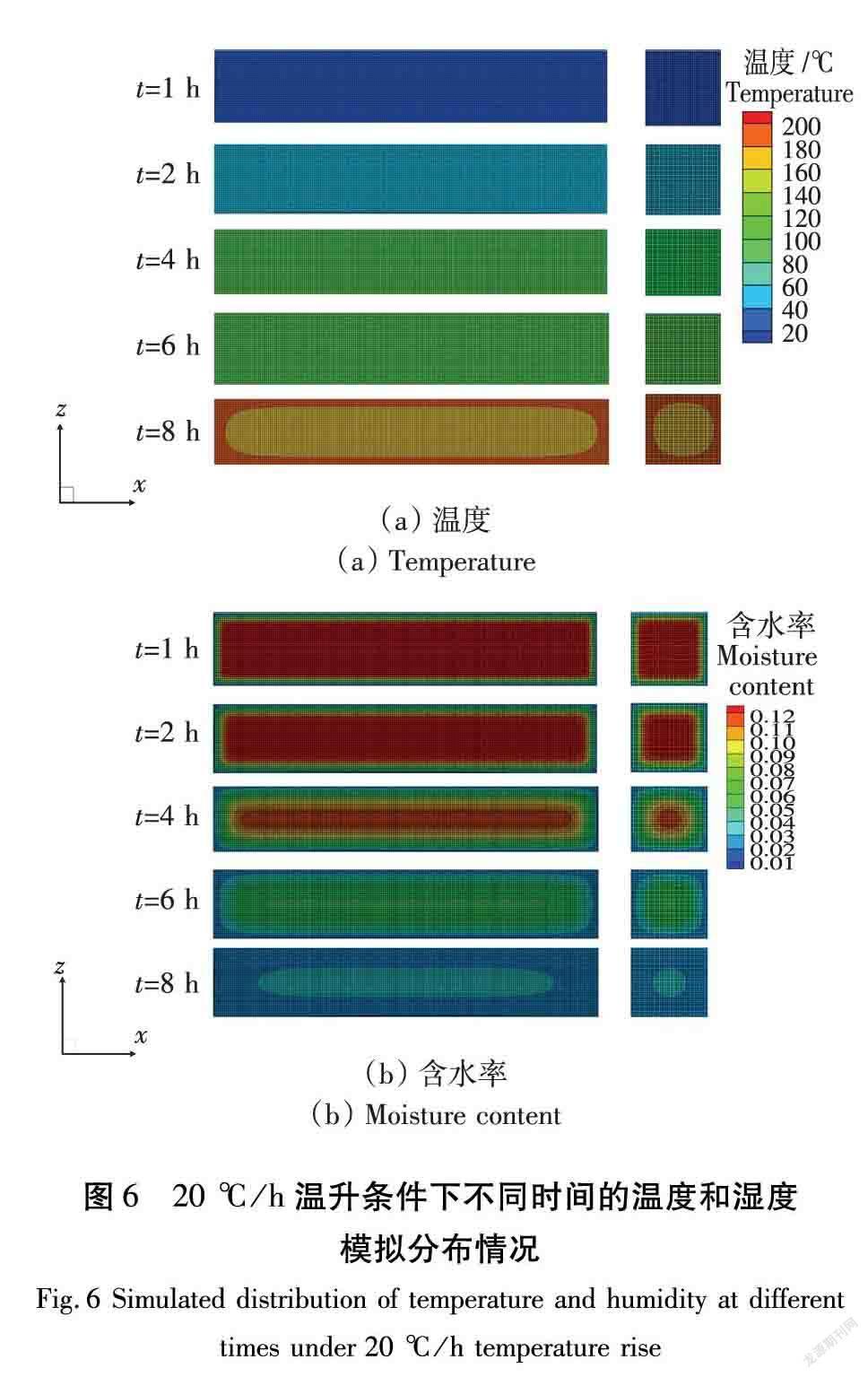
从木材的加热开始，到木材冷却，结束干燥过程，自始至终存在着不稳定热交换。因此掌握干燥过程中木材内部尤其是厚度上的温度场分布及其变化规律，对于提高木材干燥质量具有重要意义。干燥实验采用称重法测量木材干燥过程中的平均含水率情况，无法给出干燥过程中某一时刻的木材内部含水率和温度分布情况，计算完成后，使用Tecplot2018后处理软件可得出任意时刻的温度和含水率的整体分布状况，从而对干燥工艺改进提供仿真模拟条件，现给出20 ℃/h温升条件下随机时刻的温度和含水率分布情况，模拟的位置为长200 mm和宽（或高）35 mm的中心层，如图6所示。

因为木材是各向异性的，本文中的模型优点在于考虑木材在3个方向导热系数不同保证仿真精度的同时，所需要的参数较少，并且计算时间短。

3 波動干燥工艺研究

3.1 波动干燥基准

对一些硬阔叶树材进行干燥处理时，常规干燥极易产生较大的含水率梯度， 使木材产生开裂翘曲或其他缺陷。而采用波动干燥基准，在干燥过程的特定含水率阶段， 采用“升温—降温—升温”的处理方式， 达到降低干燥过程中木材开裂的可能性。

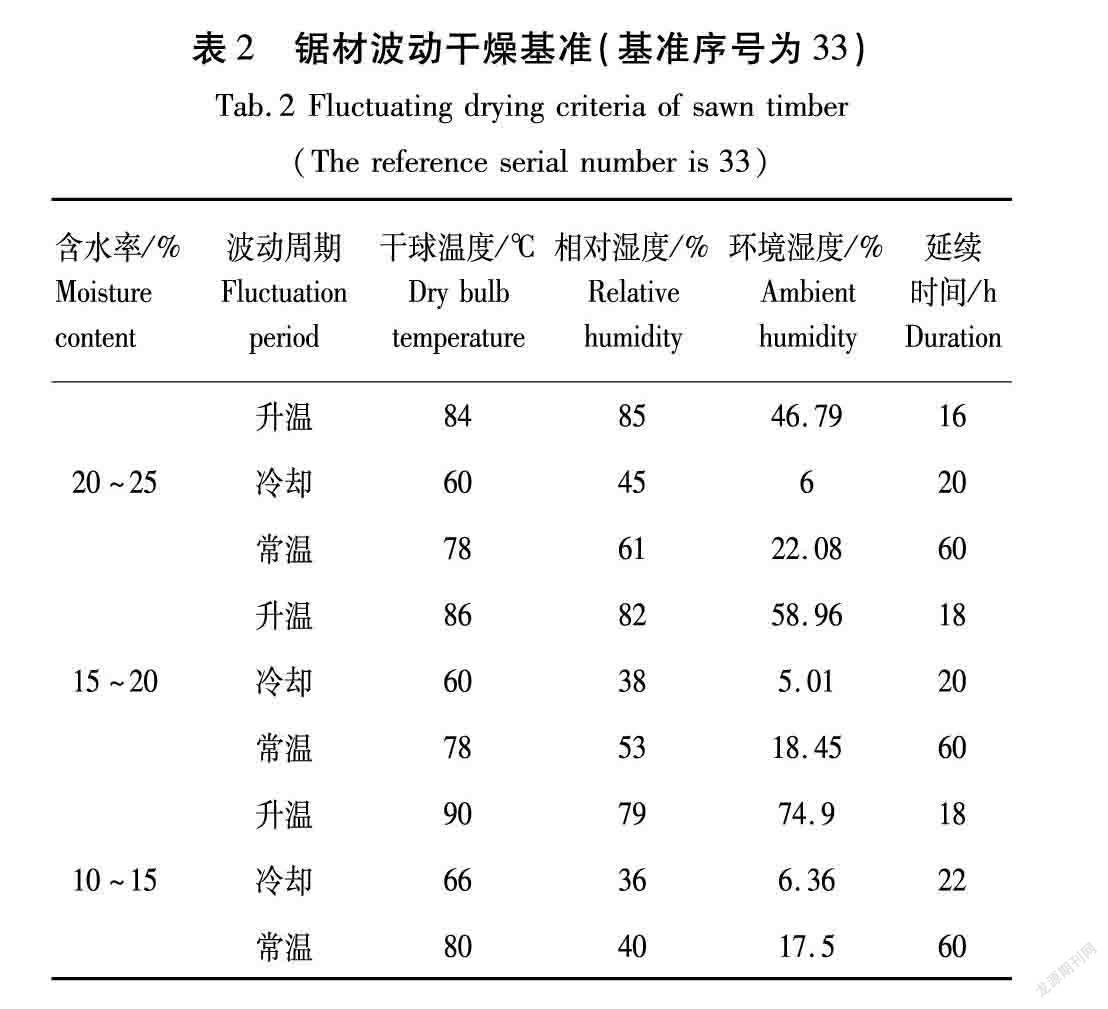
根据木材干燥基准选择表和锯材波动干燥基准[19]（仅展示表格所用部分见表2），桦木厚度尺寸在68～77 mm应选用33号干燥基准，桦木密度和各个参数使用模型构造时的参数，仿真研究初始含水率在25%阶段，三维尺寸根据我国现行锯材产品标准GB/T 4817—2019 阔叶树锯材。选用厚度为x（x=50、60、70、80 mm）×宽200 mm×长1 000 mm锯材的波动干燥工艺。扩散模型验证实验中采用的是干球温度，所以仿真过程整体采用干球相对湿度[19]为湿空气中实际水蒸气的含量与同温度下可能含有的最大水蒸气量之比，即未饱和空气的绝对湿度1 000ρsz与同温度下饱和湿空气的绝对湿度1 000ρbh之比[19]，用符号φ表示。

φ=ρszρbh×100%。（14）

环境湿度可表示为：

Mg=622φ·Pbh/（P-φPbh）。（15）

由表2可知，波动干燥过程中的温度和环境湿度情况锯材波动干燥基准，初始湿度为相对湿度85%的转换参数46.79%，初始温度为25 ℃，4组仿真均采用同一自定义边界条件，但木材的2个端面采用zeroGradient（OpenFOAM中的边界条件类型）的边界条件类型，即木材的2个端面不产生对外的温湿度扩散，从而保证木材中每一个端面平行的切面温度和湿度在同一时间的相同性。

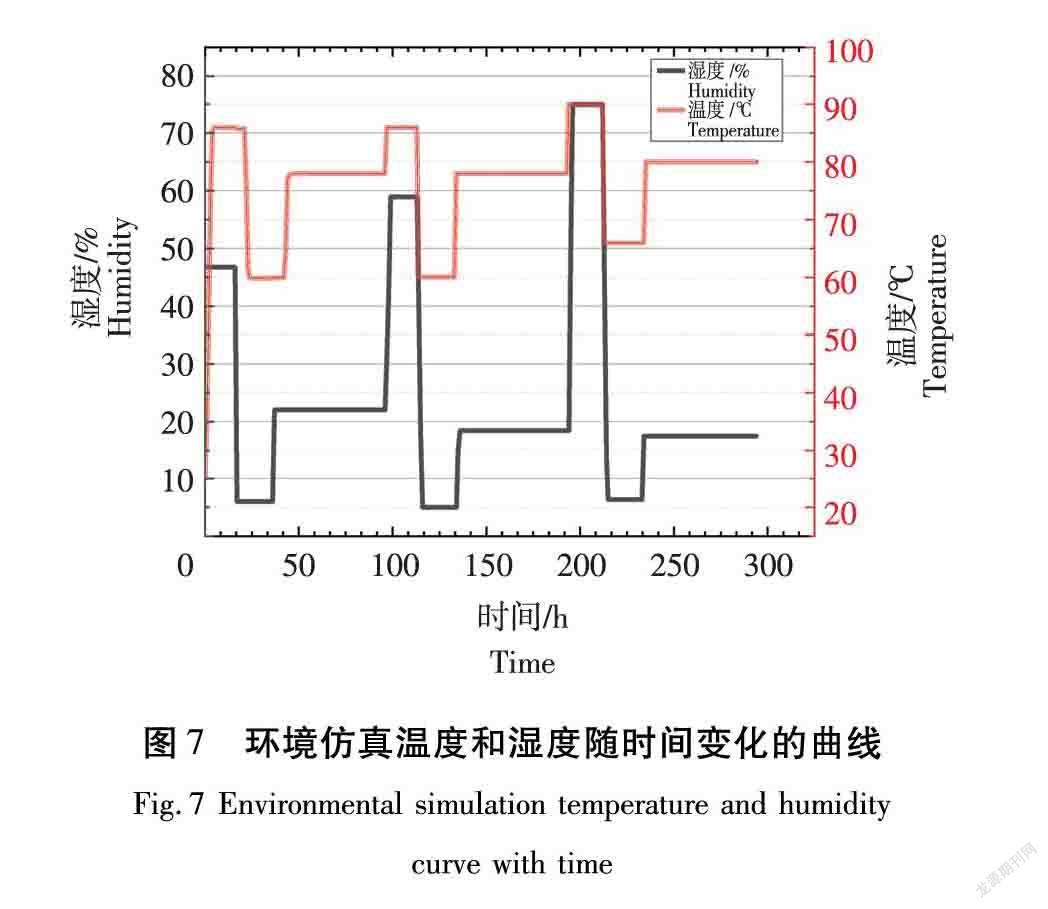
温度和环境湿度随时间变化的情况如图7所示，其中温度变化为±20 ℃/h，湿度变化为±20%/h，湿度变化的小数部分不再进行细致的时间换算。

3.2 仿真结果和分析

采用波动干燥工艺进行模拟仿真3个周期， 通过对干燥基准中相对湿度的参数转换可以看出，在升温阶段环境湿度大于木材的含水率，相当于常规干燥过程中的预热阶段，目的是使木材温度提升到要求的介质状态，并保持一定的时间，让木材本身的热度均匀，在此过程中木材的水分一般不蒸发，且可能会有少量的吸湿过程，但在模拟过程中，该过程做简化处理，即环境的含水率高于纤维饱和点时，木材中的水分不向外进行扩散，木材也不产生吸湿效应，即木材中的平均含水率无变化，为实现此过程需要更新自定义边界条件命名为（Mcustom），即自定义的含水率边界中添加if条件语句进行遍历搜寻和对比。

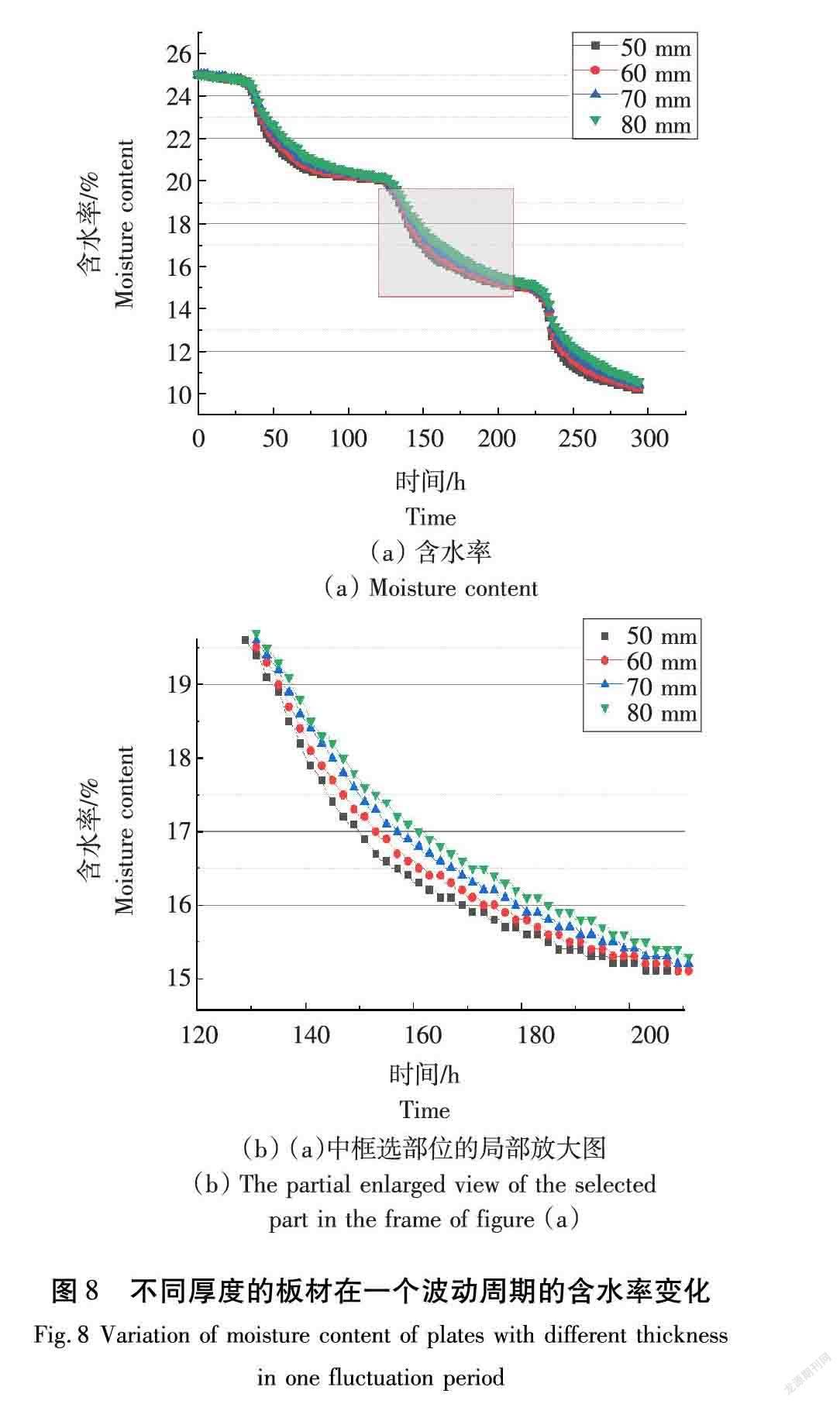
从图8可以看出，木材在升温阶段含水率基本不产生变化，这是因为环境湿度为46.79%，大于木材内部含水率，导致木材内部水分无法向外扩散，本次仿真简化掉木材的吸湿过程。在冷却阶段环境湿度为6%，木材中的水分向外扩散，且含水率梯度明显大于第三阶段的常温阶段（环境湿度为22.08%），但在冷却阶段的温度小于常温阶段，目的是为了降低木材中含水率下降的速度过快对木材产生开裂翘曲等缺陷的影响。4次不同厚度板材的干燥仿真实验表明，板材的干燥速度与厚度有着至关重要的关系。厚度越小，其干燥速度越快。但是厚度越小，则木材内部含水率梯度也就越大，而相应的应力也就越大，容易产生干裂和变形。

3.3 温度参数影响

本文中影响仿真结果的主要参数有干燥温度、环境湿度和各个周期的干燥时长，本文从干燥温度单方面采用单一变量的原则，研究干燥温度参数的改变对干燥过程中含水率梯度的模的影响。

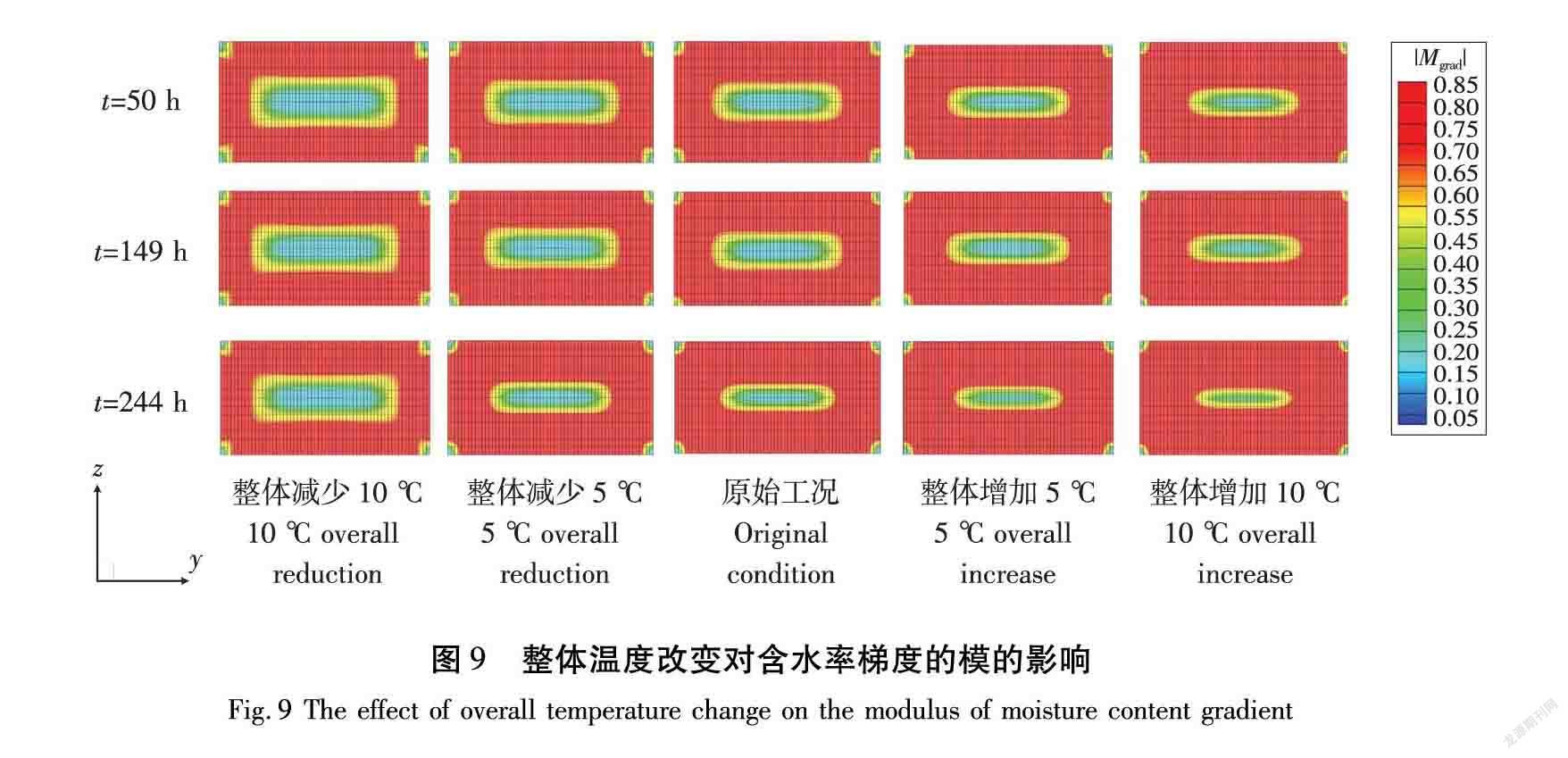
将干燥温度分别升降5、10 ℃，初始时刻的温度和温升速度不变，研究70 mm厚度板材在不同温度工况下含水率梯度的模的大小分布情况，数据记录为每1 h一次，对比相同时刻下的含水率梯度的模的大小如图9所示。含水率梯度的模计算公式为：

Mgrad=Mx2+My2+Mz2。（16）

式中，|Mgrad|为含水率梯度的模。

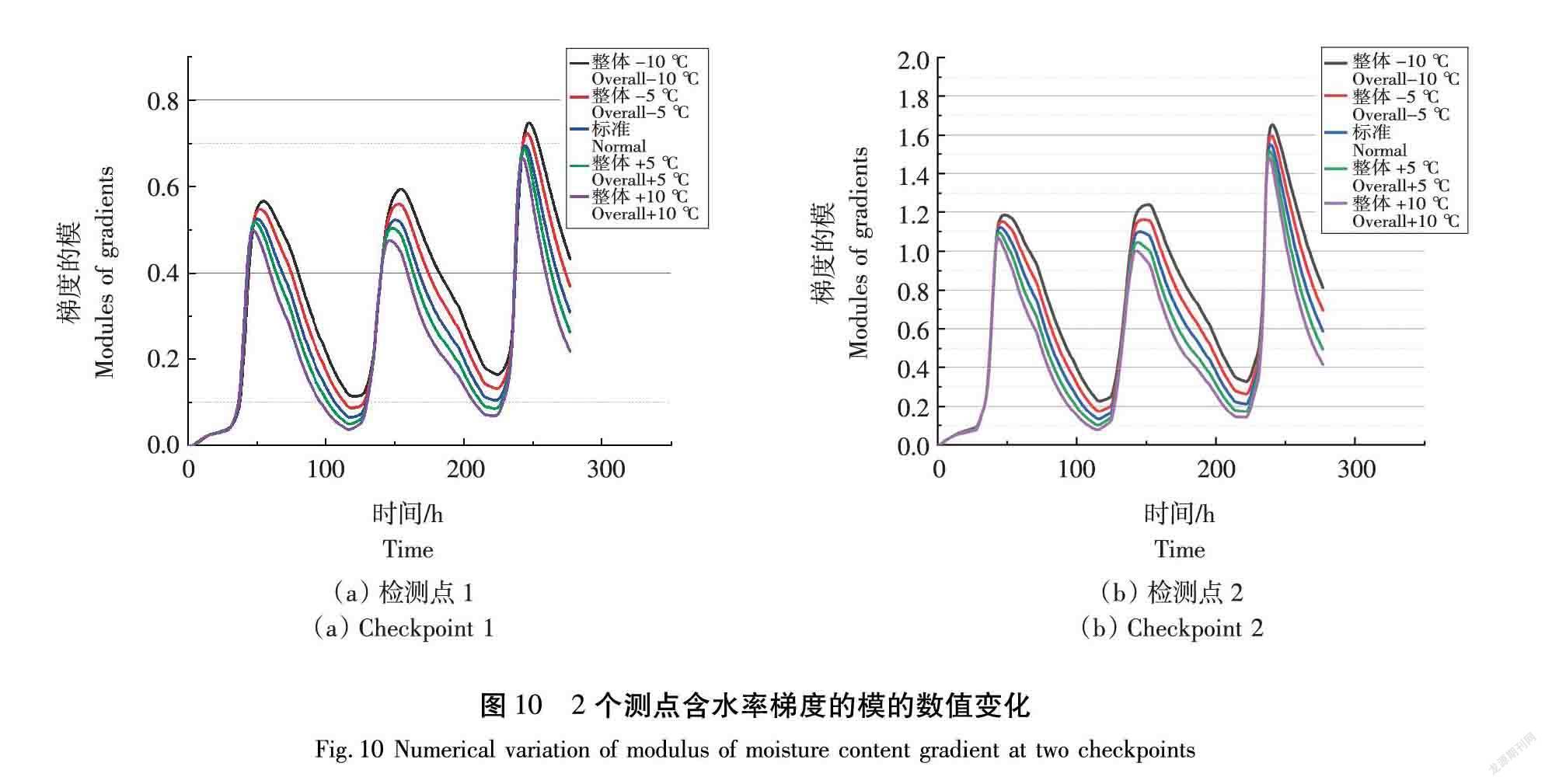
从图9可以在看出，每个时间点均为各独立波动干燥周期中高含水率梯度的模所占区域最大的时刻，随着整体温度的升高，在同一时刻高含水率梯度的模所占区域在逐渐增大，且4个边角梯度的模也在逐渐增大。现以木材切面的形心为原点，120 mm边为x轴，70 mm边为y轴，建立坐标系，以mm为分度单位，选取2个检测点：1（0，7）、2（0，14）。

从图10可以看出，不同工况下同一测点的含水率梯度的模的峰值随着温度的增大而增大，且越接近木材的表层梯度的最大值越大，在3个波动干燥周期中，最大值均出现在第3个干燥周期，这主要是因为第3个周期的升温和冷却的干球温度温差较大，所以在实际的工艺制定中，可考虑减少该周期的温度差来减小峰值的大小，达到优化干燥工艺的目的。

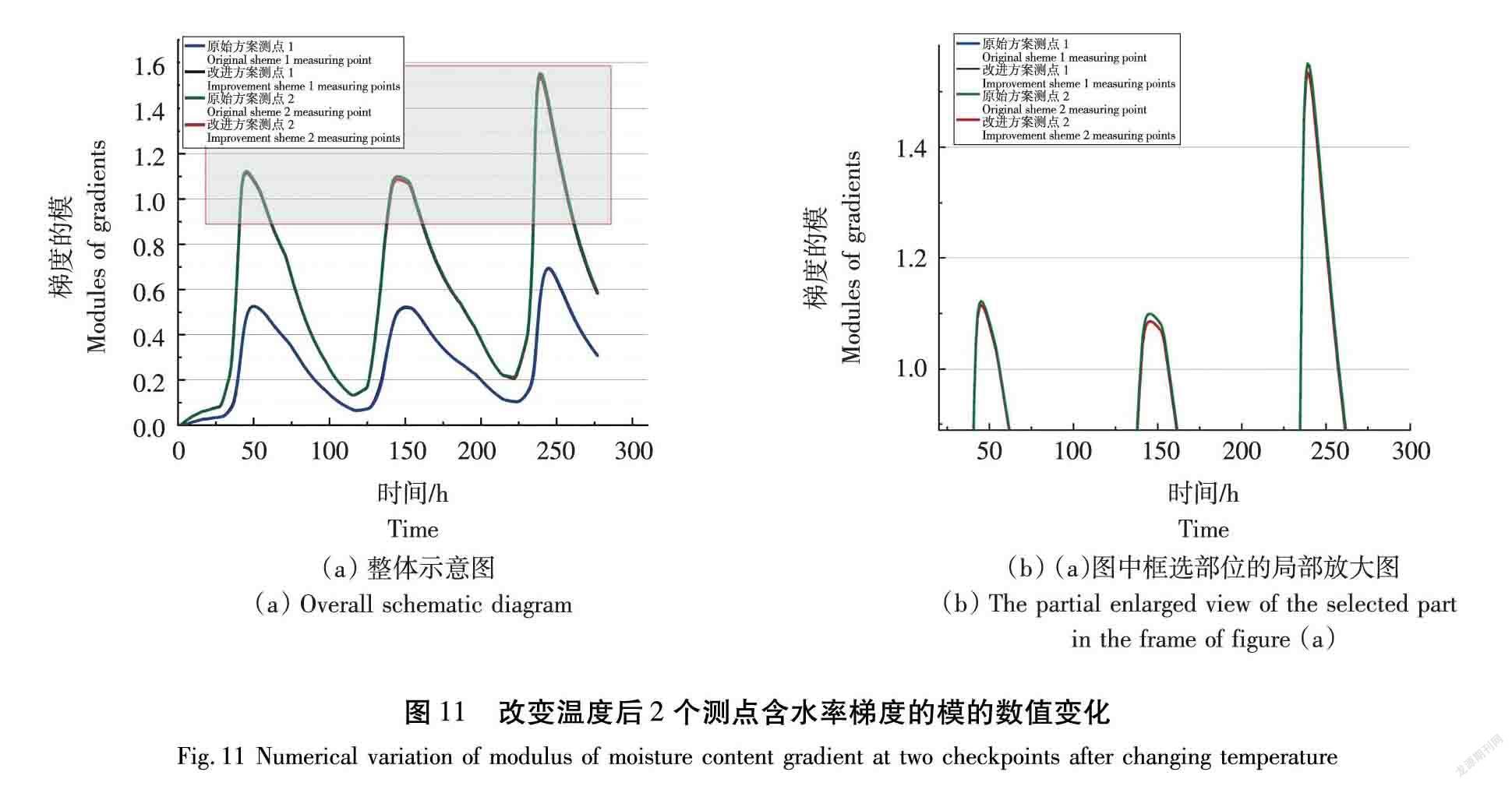
现针对干燥过程中的温度参数进行单独改变，即增大第1第2波动干燥工艺中冷却阶段温度至65 ℃，第3阶段冷却温度增加至71 ℃，其他阶段的温度不变进行仿真模拟实验，选取相同测点进行含水率梯度的模对比，结果如图11所示。

从图11可以看出，改变冷却阶段温度对测点1梯度的模影响较小，测点2的2个波峰的峰值均有减小，分别在45 h时下降0.632%;在146 h时下降1.222%;在239 h时下降1.188%，说明适当提升冷却阶段的温度、改变温差，对减小含水率梯度的模有效。

4 结论

本文通过OpenFOAM软件建立桦木板材的干燥模型，与实际数据进行对比验证，并通过该模型对桦木板材的波动干燥工艺进行的分析和优化，具体结论如下。

（1）所建桦木干燥模型的4个精度的网格密度对于仿真结果的影响不明显，平均误差分别为3.354%、3.297%、3.251%、3.204%，该模型与实验数据的平均误差均在5%以内。

（2）对厚为50～80 mm、25%初始含水率的桦木板材，采用3个标准波动干燥工况，仿真显示木材在干燥过程中含水率的变化梯度的模的大小随着板材厚度增加而减小。

（3）对于厚为70 mm、25%初始含水率的樺木板材干燥到10%，采用波动干燥工艺时通过提高5 ℃干燥过程中的冷却阶段的温度可使干燥过程中含水率梯度的模的值在3个波峰处分别下降0.632%、1.222%、1.188%。

【参 考 文 献】

[1]李建荣，冯立宁，陈广元，等.木材干燥室框架热损失研究[J].森林工程，2012，28（2）：42-46.

LI J R， FENG L N， CHEN G Y， et al. Research on heat loss of the framework of wood drying chamber[J]. Forest Engineering， 2012， 28（2）： 42-46.

[2]贾潇然，刘珊杉，周雅菲，等.循环风速对桦木干燥速度影响的研究[J].森林工程，2019，35（6）：42-47.

JIA X R， LIU S S， ZHOU Y F， et al. Study on the effect of circulation velocity on drying rate of birch[J]. Forest Engineering， 2019， 35（6）： 42-47.

[3]周永东，高鑫，付宗营，等.50 mm厚进口辐射松锯材高效干燥工艺[J].木材工业，2019，33（3）：45-48，56.

ZHOU Y D， GAO X， FU Z Y， et al. High efficient drying schedules for imported radiata pine lumber in 50 mm thickness[J]. China Wood Industry， 2019， 33（3）： 45-48， 56.

[4]周永东，高鑫，付宗营，等.25 mm厚进口桃花心木干燥基准的优化[J].木材工业，2019，33（3）：41-44.

ZHOU Y D， GAO X， FU Z Y， et al. Optimization of drying techniques for imported mahogany lumber in 25 mm thickness[J]. China Wood Industry， 2019， 33（3）： 41-44.

[5]付宗营，陈媛，甘家兵，等.栓皮栎锯材常规干燥工艺探讨[J].木材工业，2020，34（3）：52-55.

FU Z Y， CHEN Y， GAN J B， et al. Evaluation of conventional kiln drying schedule for native oriental oak lumber[J]. China Wood Industry， 2020， 34（3）： 52-55.

[6]韦妍蔷，姜帅成，李昀彦，等.过热蒸汽处理对马尾松木材干燥质量的影响[J].木材工业，2017，31（6）：50-53.

WEI Y Q， JIANG S C， LI Y Y， et al. Effect of superheated steam drying on drying quality of Masson pine lumber[J]. China Wood Industry， 2017， 31（6）： 50-53.

[7]周凡，周永东，高鑫，等.黑木相思木材干燥特性及干燥工艺制定[J].浙江农林大学学报，2020，37（3）：571-577.

ZHOU F， ZHOU Y D， GAO X， et al. Drying characteristics and drying schedule developed of Acacia melanoxylon wood[J]. Journal of Zhejiang A & F University， 2020， 37（3）： 571-577.

[8]HE Z B， QIAN J， QU L J， et al. Simulation of moisture transfer during wood vacuum drying[J]. Results in Physics， 2019， 12： 1299-1303.

[9]LI C Y， KANG C W， ZHAO X F. Moisture transverse moving mechanism during presteamed oak lumber drying[J]. Scientific Reports， 2019， 9： 18228.

[10]周正，孙丽萍.木材干燥过程含水率和温度变化的数学模型研究[J].森林工程，2014，30（1）：49-51.

ZHOU Z， SUN L P. A computational model of wood moisture content and temperature variation during drying process[J]. Forest Engineering， 2014， 30（1）： 49-51.

[11]SOKOLOVSKYY Y， SINKEVYCH O， LEVKOVYCH M， et al. The use of cellular automata in the study of heat and mass transfer processes in particular during wood drying[J]. IOP Conference Series： Materials Science and Engineering， 2021， 1016： 012017.

[12]赵景尧，蔡英春，付宗营.木材干燥过程热质迁移数学模型研究现状[J].北京林业大学学报，2015，37（7）：123-128.

ZHAO J Y， CAI Y C， FU Z Y. Present status of research on mathematical models of heat and mass transfer during wood drying[J]. Journal of Beijing Forestry University， 2015， 37（7）： 123-128.

[13]吴义强.木材科学与技术研究新进展[J].中南林业科技大学学报，2021，41（1）：1-28.

WU Y Q. Newly advances in wood science and technology[J]. Journal of Central South University of Forestry & Technology， 2021， 41（1）： 1-28.

[14]BARONAS R， IVANAUSKAS F， SAPAGOVAS M. Modelling of wood drying and an influence of lumber geometry on drying dynamics[J]. Nonlinear Analysis： Modelling and Control， 1999， 4： 11-22.

[15]RAISUL ISLAM M， HO J C， MUJUMDAR A S. Simulation of liquid diffusion-controlled drying of shrinking thin slabs subjected to multiple heat sources[J]. Drying Technology， 2003， 21（3）： 413-438.

[16]吕超，詹天翼，王旋，等.木材内部水分扩散特性研究现状及发展趋势[J].世界林业研究，2019，32（6）：43-48.

LYU C， ZHAN T Y， WANG X， et al. Research on water diffusion characteristics in wood[J]. World Forestry Research， 2019， 32（6）： 43-48.

[17]ZHENG S J， SONG K Y， ZHAO J Y， et al. Inverse estimation of effective moisture diffusivity in lumber during drying using genetic algorithms[J]. BioResources， 2016， 11（4）： 8226-8238.

[18]KOCAEFE D， YOUNSI R， PONCSAK S， et al. Comparison of different models for the high-temperature heat-treatment of wood[J]. International Journal of Thermal Sciences， 2007， 46（7）： 707-716.

[19]王喜明.木材干燥學[M].3版.北京：中国林业出版社，2007.

WANG X M. Wood drying[M]. 3rd Edition. Beijing： China Forestry Publishing House， 2007.