黎曼扭曲乘积流形中的完备超曲面*

张 宁

(河南工学院 理学部,河南 新乡453003)

0 引言

黎曼流形中的超曲面一直是几何学家所钟情的研究领域,也是数学的中心之一。它与偏微分方程、复分析、函数论、拓扑学以及微分几何的各个方向都有深刻的联系,且已经推广到了高维和高余维。这其中有个非常重要的唯一性问题,即Bernstein问题。对于欧氏空间中的极小超曲面,Bernstein问题已经有了很好的解答,极小超曲面的维数n≤7时,Fleming[1]、De Giorgi[2]、Almgren[3]和Simons[4]证明了Bernstein定理成立,即当极小超曲面可表示为整体图时一定是平坦的。但是当极小超曲面的维数n≥8时,Bombieri、De Giorgi和Giusti[5]给出了著名的反例。此外在高余维,Lawson和Osserman[6]也证明了存在反例,那么接下来需要寻找使得Bernstein定理成立的最佳条件。近几年来,几何学家们对这个困难的问题做出了一些有趣的研究,如将关于超曲面唯一性的研究拓展到更广的外围空间领域。

本文主要研究黎曼扭曲乘积流形中超曲面的唯一性。此外,黎曼扭曲乘积流形是由一个正定义的区间作为基,一个黎曼流形为纤维,一个正定的光滑函数为扭曲乘积函数。在详细给出我们的结果之前,先简要介绍一下与我们的结果相关的一些最近的研究结果。

Montiel[7]研究了常平均曲率紧致超曲面浸入黎曼扭曲乘积流形中的唯一性,且要求纤维的Ricci曲率和扭曲乘积函数满足NCC融合条件。之后,文献[8,9]拓广了[7]中的结论到完备非紧致超曲面。Alias、Impera和Rigoli[9]通过应用推广的Omori-Yau极大法则将[8]中结果延拓到常高阶平均曲率。

我们发现关于该唯一性问题的很多研究成果都有相似的要求,即截面曲率有界且满足合适的融合条件。基于已知的研究成果,本文旨在利用弱极大值法则证明黎曼扭曲乘积流形中抛物的完备超曲面的新的唯一性结果。第一部分给出黎曼扭曲乘积流形及其超曲面的一些概念与结论;第二部分证明黎曼扭曲乘积流形中的抛物的完备超曲面的唯一性结果;第三部分将所得的唯一性结果推广至高阶平均曲率。此外,作为定理的应用我们考虑了一类特殊的超曲面即浸入乘积空间中的超曲面,给出了此超曲面的一些刚性结果。

1 黎曼扭曲乘积流形及其超曲面

本节主要回顾黎曼扭曲乘积流形及其超曲面的一些基本理论和基本方程等基础知识。

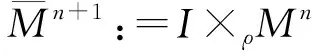
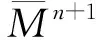
令A:Τ(Σ)→Τ(Σ)是超曲面Σn上关于N的形状算子。则对于任意点p∈Σn,A限制了一个自共轭线性算子Ap:Τp(Σ)→Τp(Σ),并且其特征值λ1,…,λn为超曲面Σn的主曲率。此外,对于形状算子Ap,超曲面Σn上存在n个代数不变量,即关于Ap特征值的r阶初等对称函数Sr,定义为

我们注意到形状算子A的特征多项式满足:

此外,超曲面Σn上的r阶平均曲率Hr被定义为

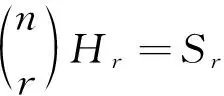
(1)

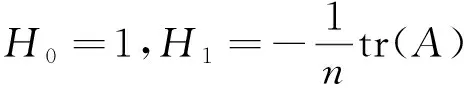
我们定义A相对应的牛顿变换Pr:Τ(Σ)→Τ(Σ)为

Lr(f)=tr(PrHessf)

其中Hessf:Τ(Σ)→Τ(Σ)是f的Hessian算子且等价于

〈Hessf(X),Y〉=〈Xf,Y〉,X,Y∈Τ(Σ)

此外,由(1)式可知,若Lr是椭圆算子当且仅当牛顿变换Pr是正定的。显然,L0=Δ是椭圆算子。

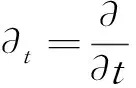
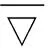
故,高度函数h在Σn上的梯度表达式为

特别地,

其中,( )Τ是向量场沿Σn的切丛,而||为向量场在Σn上的范数。

为了证明我们的结论,我们需要用到文献[9]的如下结果:

引理1 设ψ:Σn→I×ρMn是浸入黎曼扭曲乘积流形I×ρMn中的超曲面。令h是高度函数,σ(t)是扭曲乘积函数ρ(t)的原函数,则

Lrh=(logρ)′(h)(crHr-〈Prh,h〉)+crθHr+1

(2)

Lrσ(h)=cr(ρ′(h)Hr+θρ(h)Hr+1)

(3)

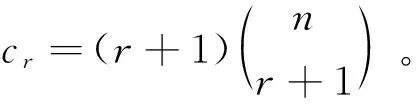
接下来,给出我们的主要分析工具,弱极大值法则[11]。

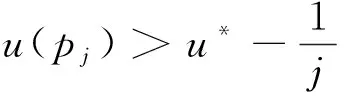
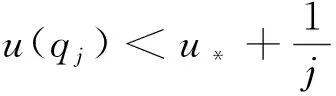
此外,流形F满足弱极大值法则当且仅当F是随机完备的。

2 黎曼扭曲乘积流形中的唯一性结果

在本节中,我们将给出有关黎曼扭曲乘积流形中完备超曲面的主要结果。此外,黎曼扭曲乘积流形I×ρMn中的有界块是指如下类型的区域:

[t1,t2]×Mn={(t,p)∈I×ρMn:t1≤t≤t2}

通过应用弱极大值法则,下面我们给出关于平均曲率H,角度函数θ和扭曲乘积函数的导数ρ′三者之间的正负符号关系,此结果推广了作者在文献[12]中命题8的结论。

引理2 设ψ:Σn→I×ρMn为具有非零平均曲率的完备超曲面,且包含于I×ρMn的有界块中。若H>0,θ在Σn上不变号,并且在Σn上弱极大值法则对Laplacian算子Δ成立。假设以下两个条件中的任意一个成立:

(i)(logρ)′′≥0,(ii)扭曲乘积函数ρ单调,则ρ′(h)θ≤0。另一方面,若H<0,则ρ′(h)θ≥0。

证明:由于超曲面包含于一有界块中,可知h是有界的。首先由h*=infΣh>-∞和弱极大法则在Laplacian算子上成立,可得存在点列{pj}⊂Σn使得

则

(4)

类似地,利用h*=supΣh<+∞,可找到点列{qj}⊂Σn使得

则

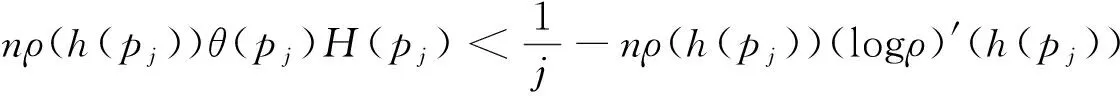
(5)

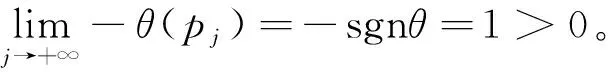
(6)

因此(logρ)′(h*)≥0。由(i)(logρ)′′≥0,有

0≤(logρ)′(h*)≤(logρ)′(h)

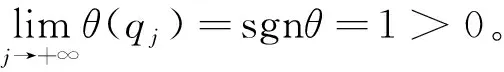
(7)

所以(logρ)′(h*)≤0。利用(logρ)′′≥0,则

(logρ)′(h)≤(logρ)′(h*)≤0

综上所述,当(i)(logρ)′′≥0时,结论成立。

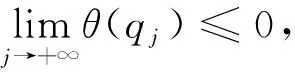
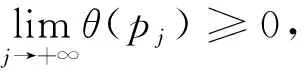
另一方面,由以上证明过程我们还可得如果H<0且角度函数θ不变号,则有ρ′(h)θ≥0。

接下来,我们将证明黎曼扭曲乘积流形中抛物超曲面的唯一性结果。首先,我们给出下面的引理,并且此引理拓展了文献[12]中命题7的相应结论。

引理3 设M是抛物的黎曼流形,u∈C2(M)是M上的正的光滑函数且u*=supMu<+∞。如果Δu在M上定号,则u在M上是常数。

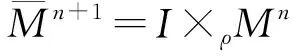
证明: 由于Σn是抛物的,利用文献[13]中的推论6.4可知Σn是随机完备的超曲面,故在Σn上弱极大值法则对Laplacian算子Δ成立。此外,结合定理1中的条件,可得引理2成立。

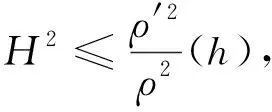
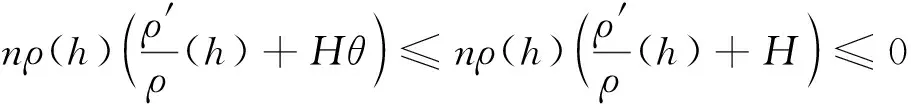
此外,因为σ(h)在Σn上有界,所以存在常数C使得σ(h)≤C。利用引理2,可知σ(h)是常数,故,高度函数h也是常数。因此,Σn是一类空片。

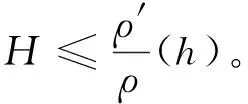
同理可证Σn是一类空片。

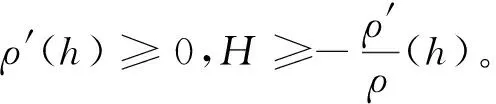
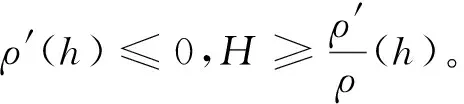
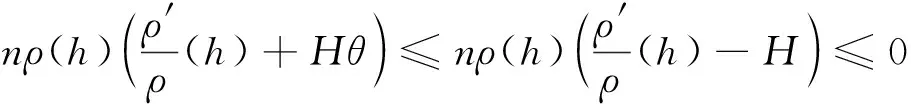
接下来,类似于H>0中的讨论, 我们可得Σn是一类空片。

考虑外围空间为乘积空间I×Mn,作为定理1的应用,我们可得如下结论。

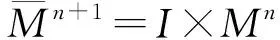
证明:由等式(2),可知

Δh=nHθ

因为θ和H均在Σn上不变号,所以Δh在Σn上也不变号。类似于定理1的证明,我们有Σn是一类空片。

3 延拓至高阶平均曲率

在这一节, 我们延拓第2节中唯一性的结论至高阶平均曲率超曲面上。首先,我们给出引理2拓展至高阶平均曲率的情况。

已知,若超曲面上p0∈Σn处所有的主曲率ki(p0),1≤i≤n符号相同,则称点p0为Σn上的椭圆点。

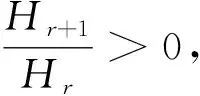
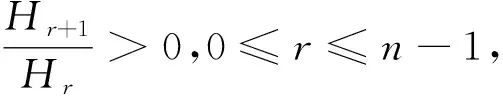
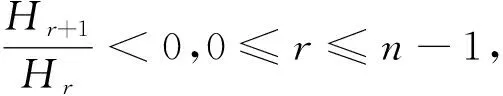
下面,我们将定理1的结论推广到高阶平均曲率上,可得定理2,并且定理2拓展了文献[14]中的相应结论。

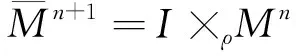
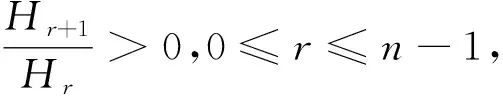
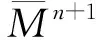
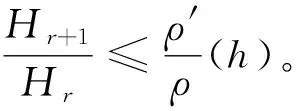
因为Pr在Σn有上界,所以存在常数β满足Pr≤βI,即Lrσ(h)≤βΔσ(h)。

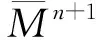
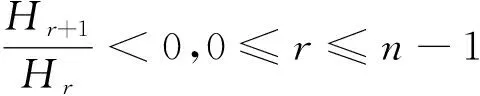
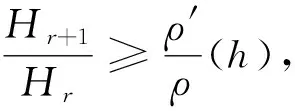
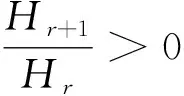
类似于推论1,我们可得如下结论。

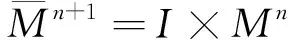
证明:由等式(2)可得

Lrh=crHr+1θ

结合假设条件有Lrh在Σn上不变号,类似于定理2的证明可知Δh在Σn上也不变号。利用引理3有高度函数h在Σn上是常数,所以Σn是一类空片。