基于改进矩阵分解算法的推荐方法研究
田海梅
(金陵科技学院计算机工程学院,江苏 南京 211169)
随着互联网飞速发展,信息数量不断增长,而人收集、鉴别信息的能力有限,于是推荐系统的重要性显现出来。推荐系统[1-2]分析用户的历史行为和爱好需求,使用合适的推荐算法挖掘用户的潜在兴趣,来为用户提供有价值的推荐。推荐一般有两个目的,一个是激发用户去做某个事情,另一个是解决信息过载问题。按照建模方式的不同,推荐系统分为协同过滤推荐、基于知识的推荐、基于内容的推荐和多种特征混合推荐等。目前推荐系统已经运用到很多方面,比如商品平台和社交平台等[3]。许多电商通过推荐系统来给用户进行个性化推荐,帮助用户快速发现感兴趣的商品从而给企业带来可观的收入[4-6]。
在众多协同过滤推荐算法中,矩阵分解算法具有可扩展性并易于实现,成为最为普遍和最受欢迎的一种协同推荐算法。在推荐系统中,矩阵分解算法可以解决数据的稀疏性问题,比其他协同过滤推荐算法更节省内存,更精确。一般情况下矩阵分解将构建的用户与项目对应的评分矩阵分解为两个低维矩阵乘积,因没有考虑项目与项目之间的非对称相似性问题,最终推荐结果不理想。为了解决这一问题,一些学者已经提出了解决方法。文献[7]提出通过信任感知来进行矩阵分解,从而提高推荐系统的准确性。文献[8]和[9]分别提出利用项目与项目属性之间的相互关系来进行矩阵分解,以及通过一种用户间的非对称的相似性方法来进行矩阵分解,从而达到推荐的效果。以上方法都没有考虑项目本身的潜在知识信息。本文在矩阵分解技术的基础上融入项目本身潜在的知识信息,加上项目与项目之间的不对称相似度,从而提高推荐算法的准确率。
1 推荐系统的预备知识
1.1 隐向量
对项目与用户之间的评分矩阵进行传统的矩阵分解得到的向量,称为低维向量[10]。在推荐系统中,用户(User)对物品(Item)的推荐评分,用物品和用户对应的隐向量的内积来表示[11-12]。
1.2 传统的矩阵分解算法
矩阵分解算法的主要思想是:首先构造一个由用户ID、项目ID、评分组成的评分矩阵。然后将构建的评分矩阵通过传统的矩阵分解算法转化成两个低维特征矩阵的乘积。最后通过这两个低维特征矩阵去估算那些没有做出评价的缺失项目[13-14]。
矩阵分解中用户的隐藏特征矩阵用P表示,项目的隐藏特征矩阵用Q表示。矩阵分解首先对构建的原始评分矩阵R进行分析,然后学习矩阵P和Q,最后缺失项用R来表示,R由P和Q预测。
设P∈RK×N和Q∈RK×M,其中向量的维数用K表示,K≪min(N,M),然后用分解的低维矩阵P和Q的乘积来近似表示R,如公式(1)所示:
R≈PTQ
(1)
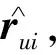
(2)
传统的矩阵分解利用损失函数和误差平方最小化来不断学习矩阵P和Q,如公式(3)所示:
(3)

通过传统的矩阵分解算法得到用户u与项目i的隐向量,虽然降低了隐向量的维度,但是并没有该用户及其评价过的项目特征的许多附件信息,用户u的隐向量跟真实情况之间有一些差别[15-18]。
1.3 加权非对称(asymmetric)的相似性度量方法
定义1给定关联开放数据(linked open data,LOD)中两个资源r,s∈R,Fr和Fs分别表示它们的特征集合,Fr∩Fs是r和s的共同特征,r和s共同的分区信息内容(partitioned information content,PIC)值占r的PIC值的比例由公式(4)定义,占s的PIC值的比例由公式(5)定义:
(4)
(5)
CPIC的取值范围为[0,1],CPIC是一种非对称的方式,即CPIC(r,s)≠CPIC(s,r)。
EPIC(r,s)=1-exp(-CPIC(r,s))
(6)
EPIC(s,r)=1-exp(-CPIC(s,r))
(7)
EPIC的取值范围为[0,1],EPIC是一种非对称的方式,即EPIC(r,s)≠EPIC(s,r)。
定义2给定LOD中两个资源r,s∈R,Fr和Fs分别表示它们的特征集合,Fr-Fs表示在r中而不在s中的特征,Fs-Fr表示在s中而不在r中的特征。两个资源之间差异化的DPIC由公式(8)和公式(9)定义:
(8)
DPIC(r,s)=DPIC(s,r)
(9)
DPIC的取值范围为(0,1],DPIC是一种对称的度量方式,分母加1是防止分母为0。本文采用以上两个概念EPIC和DPIC,提出了一种基于PIC的非对称的语义相似度计算方法AEPICSS,用来计算LOD中资源之间的相似度,AEPICSS由公式(10)和(11)定义:
AEPICSS(r,s)=EPIC(r,s)·DPIC(r,s)
(10)
AEPICSS(s,r)=EPIC(s,r)·DPIC(s,r)
(11)
AEPICSS的取值范围为[0,1],因为CPIC是非对称的,AEPICSS显然是一种非对称的基于LOD的项目相似度计算方法,即AEPICSS(r,s)≠AEPICSS(s,r)。
2 改进的矩阵分解算法在推荐系统中的应用
2.1 改进的矩阵分解算法和不对称因子模型

图1 改进的矩阵分解模型流程
早期的基于矩阵分解的推荐算法是对用户与项目之间对应的评分矩阵进行分解,没有充分考虑项目属性附加信息,对项目与项目之间的不对称相似性问题缺乏考虑,导致推荐的准确率一般。
本文改进的矩阵分解算法的主要思想是:在早期矩阵分解的基础上融入项目本身潜在的知识信息,加上项目与项目之间的不对称相似度,从而提高推荐算法的准确率。对早期的矩阵分解方法进行改进后的流程如图1所示。
融合后的改进算法目标函数如公式(12)所示。
(12)
设有M个项目,其中rit是第i个用户对第t个项目的评分。当rit>0时,μ=1,δ=1,ε=0;当rit=0时,μ=0,δ=0,ε=1。simtj是项目t和j的相似度。其中sim用加权非对称(asymmetric)相似度来度量。
(13)
2.2 推荐系统的评价
在推荐系统中,一般采用均方差(mean square error,MSE)、均方根误差(root mean square error,RMSE)和平均绝对值误差(mean absolute error,MAE)来对比两个数值之间的不同。MSE是指估计值与真实值之间的差异值进行平方的期望值。RMSE是指预测模型对实验数据的精确度的描述,是均方差的算术平方根,RMSE越高表示精确度越低,RMSE越低表示精确度越高。实际的测值误差本文用MAE来表示。
(14)

(15)
(16)
3 实验结果与分析
本文采用MovieLens 100k、MovieLens 1M和Netflix数据集。MovieLens是用户对电影评分的数据集,包括用户ID、电影ID和用户对电影的对应评分,MovieLens 100k与MovieLens 1M由GroupLens公司提供。Netflix数据集由Netflix公司提供,由于该数据集十分庞大,本文从中随机选取990个用户在1 499个物品上的49 933条评分记录,且每个用户至少对20部电影进行评分。这3个数据集都被广泛用于推荐系统研究,相关信息如表1所示。

表1 数据集统计结果
本文的训练数据为随机从构建好的用户项目评分矩阵中抽取70%,测试数据为评分矩阵中剩余的30%。评价指标用MSE、RMSE和MAE来表示。本文选取传统的矩阵分解(basic MF)、非负矩阵分解(non-negative MF)和SVD++模型进行了对比实验,釆用多次实验的平均值作为结果。参数设定过程中,为了与基准算法进行公平的比较,视迭代次数达到100或者训练误差小于10-6时本文模型的学习过程达到收敛。
学习速率α和正则项参数β通常设置为很小的值。用3个数据集上的RMSE来选择这两个参数,对于MovieLens 100k,α取0.003时RMSE最小,β取0.007时RMSE最小;对于MovieLens 1M,α取0.001时RMSE最小,β取0.008时RMSE最小;对于Netflix,α取0.003时RMSE最小,β取0.007时RMSE最小。特征数通常代表物品的分类数,在实验中,当特征数小于70时RMSE变化很小。在下面的实验中,选择20作为特征数。
参数设置为最优值、特征个数设置为20时的结果如表2所示。从表2可以看出,本文的改进方法优于所有的对比方法,即MSE、RMSE和MAE均低于所有的对比方法,其中在Netflix数据集上的MSE比其他方法的MSE最多提升了14.31%。本文方法的准确率,在MovieLens 100k数据集上较SVD++提高了0.9%,在MovieLens 1M数据集上较SVD++提高了6.24%,在Netflix数据集上较SVD++提高了7.81%。

表2 各方法在不同数据集上的结果
4 结 语
本文结合改进的矩阵分解荐模型和不对称因子模型的优点,在矩阵分解技术的基础上融合项目本身潜在的附加信息,并考虑项目之间的不对称相似度,从而大大提高推荐算法的准确率。同时数据的稀疏性也有所降低。改进的矩阵分解算法对整个推荐系统中的一些应用起到了很好的优化作用。从MovieLens 100k、MovieLens 1M和Netflix数据集上的实验数据来看,本文方法的MSE、RMSE、MAE值均小于所有的对比方法。实验结果表明,本文方法有效地提高了推荐的性能,可以在推荐系统中得到更好的推荐效果,这说明本文采用的不对称因子模型已经很好地整合到改进的矩阵分解中。本文的方法提升了推荐的准确性,网络线上商城、美食团购推荐平台可根据用户的历史评分和项目的属性进行推荐,给用户带来更好的使用感受;但是在空白数据填充和冷启动方面仍存在一定的问题,这将是下一步的研究方向。

