基于分布式压缩感知的煤矿井下图像采集方法研究
徐永华,刘海强,2,朱良朋,邵 斐
(1.金陵科技学院计算机工程学院,江苏 南京 211169;2.中煤科工集团常州研究院 有限公司,江苏 常州 213015;3.淮北矿业(集团)有限责任公司,安徽 淮北 235000)
煤炭是我国的主要能源,是我国国民经济发展的重要保证[1]。物联网有助于提升煤矿安全生产水平,是智能矿山的基础设施[2]。煤矿物联网存在大量无线传感节点,需要传输大量数据;但是,煤矿井下传感器存在着能量受限的问题,如果传输数据量过大,传感器能量将快速耗尽,影响无线传感器的网络寿命。因此,需要研究高效的压缩编码方法,降低网络传输数据量,延长煤矿无线传感器网络寿命。
压缩感知(compressed sensing,CS)[3]被证明是一种高效的数据压缩编码方法,但是压缩感知仅仅利用了信号内相关性,无法适应无线传感器网络既有信号内相关性又有信号间相关性的特点。分布式压缩感知(distributed compressed sensing,DCS)[3-4]能够利用信号内和信号间相关性,具有比压缩感知更高效的压缩编码性能。分布式压缩感知在编码端通过简单的非线性投影将高维信号降至低维,实现数据压缩编码;在解码端利用信号内和信号间相关性联合解码,降低了编码端的工作量,具有更高效的信息采集效率。由于这些优点,分布式压缩感知自提出以来受到研究人员的广泛关注,被应用于无线传感器网络[5]、信道估计[6]、图像融合[7-8]等领域,但在煤矿行业内应用研究较少。Zhang等[9]使用微震信号到达时间纠正信号起点,然后使用分布式压缩感知对微震信号进行压缩采集;赵小虎等[10]研究了基于傅里叶基的煤矿微震信号稀疏表示和压缩采集方法,提出了改进的联合恢复算法,但是煤矿微震信号的稀疏性与本文研究的煤矿井下图像信号有较大区别。针对煤矿井下图像信号具有相近背景信息的特点,Xu等[11]提出了一种基于归一化Bhattacharyya系数的自适应压缩和混合假设残差重建算法,结合背景减法的思想,将前景的高质量重建与背景的多假设残差重建相结合,提高了视频序列的整体重建效果,但是未分析煤矿图像信号的联合稀疏性;华倩倩[12]研究了煤矿井下分布式视频压缩感知方法,使用小波基描述信号相关性,对关键帧和非关键帧采用不同压缩率,但是主要利用了图像帧间相关性,没有利用单幅图像的内部相关性。
本文提出基于分布式压缩感知的煤矿井下图像压缩采集模型与方法,将图像划分为多个块,利用混合支撑基模型描述图像块内和块间相关性,利用低计算复杂度的确定性稀疏测量矩阵降低传感器工作量,以更快更好地恢复图像,增强算法的实时性。
1 分布式压缩感知原理
设N维信号x满足x=Ψθ,其中θ=(θ1,θ2,…,θN)T,如果θ有k个非零元素且k≪N,那么x被称为稀疏信号。分布式压缩感知理论证明,通过非线性投影y=Φx可以将高维信号x降低至低维,实现数据压缩编码。理论上,通过y恢复x有无穷多个解,但是,Donoho[3]提出的CS理论证明,当测量矩阵Φ满足RIP(路由信息协议)条件时,通过求解最优化问题即可恢复x。
根据DCS理论,对于信号xj∈RN,其中j∈{1,2,…,J},如果xj是稀疏信号,那么可以通过公式(1)对信号xj压缩编码:
yj=Φjxj
(1)
假设联合信号X=[x1,x2,…,xJ],可以通过公式(2)对J个信号联合压缩编码:
Y=ΦX=Φ[x1,x2,…,xJ]
(2)
分布式压缩感知理论证明,当X联合稀疏时,可以通过求解最优化问题恢复原信号。
1.1 信号联合稀疏表示
根据信号联合稀疏表示理论,联合信号X可以表示为:
X=ΨΘ=Ψ[θ1,θ2,…,θJ]
(3)
1.2 信号联合恢复
根据分布式压缩感知理论,如果联合信号X具有联合稀疏性,那么可以通过求解最优化问题恢复θ,即:
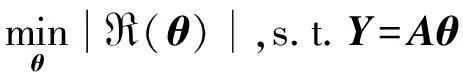
(4)
然后使用稀疏基对θ反稀疏变换,即可恢复X。
2 算法模型描述
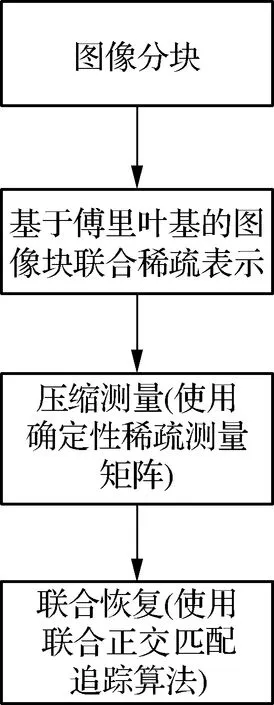
图1 基于DCS的煤矿井下图像压缩采集步骤
本算法以列向量为单位对图像进行分解,使用测量矩阵非线性投影对每个列向量压缩编码,在解码端通过求解公式(4)所示的最优化问题联合恢复原信号。本算法可以分为图像分块、图像块联合稀疏表示、压缩测量和联合恢复四步(图1)。
1)图像分块。为了更好地利用图像的相关性,本算法以列为单位将煤矿井下图像划分为255个255×1的小块xj(1≤j≤255),每个小块可以看作一个信号,从而可以利用信号内(图像块内)相关性和信号间(图像块间)相关性压缩编码。
2)图像块联合稀疏表示。将煤矿井下图像的每一列看作一个一维向量,对每个列向量进行稀疏表示。研究人员证明傅里叶变换、小波变换等可以用于信号稀疏表示,其中傅里叶变换用于图像稀疏表示时性能良好[13],因此本算法采用傅里叶基,其定义为:
(5)
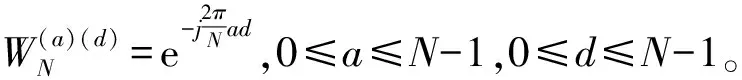
研究人员提出了4种联合稀疏模型,其中混合支撑集模型是其他模型的扩展,通用性更强,因此本算法使用混合支撑集模型[4]描述煤矿图像块内和块间相关性,其表达式为:
xj=cj+zji,j∈{1,2,…,J}
(6)
其中cj为不同图像块的公共信息部分,它体现了图像块间相关性;zji为图像块的独立信息部分,它体现了图像块内相关性。图像块的公共信息部分具有相同的非零元素位置,系数可以不同;独立信息部分可以进行稀疏表示,代表图像块的特有信息。
3)压缩测量。基于分布式压缩感知理论,本算法使用测量矩阵对图像的每列进行非线性投影实现信号压缩。现有测量矩阵包括随机测量矩阵和确定性测量矩阵。随机测量矩阵性能较好,但是每次解码均需要将测量矩阵传输至解码端,这大大增加了传输数据量;确定性测量矩阵具有确定的性能,不需传输测量矩阵,更能节省传感器能量,特别是基于二进制伪随机序列的确定性稀疏测量矩阵仅需要进行加法运算,计算复杂度低,适合计算资源受限的煤矿传感器。它的构造方法[14]如下:将确定性二进制伪随机序列h={b0,b1,…,bL}作为测量矩阵的第一列,该序列具有良好的自相关性和互相关性,通过列向量循环左移得到测量矩阵的其他列,如公式(7)构造出矩阵Q。然后从Q中随机抽取M行得到M×L大小的测量矩阵。由于二进制伪随机序列仅包含“0”和“1”两个元素,因此该测量矩阵仅需要进行加法运算,计算复杂度低。
(7)
4)联合恢复。现有联合恢复算法包括联合贪婪匹配追踪类算法[15]、混合范数法[16]、贝叶斯类算法[17]等,本文使用计算复杂度低的联合正交匹配追踪算法(simultaneous orthogonal matching pursuit,SOMP)[18]。该算法首先将压缩采样后的信号初始化为残差;然后逐步寻找与残差最相关的非零元素的位置并添加进联合支撑集,逐步迭代更新残差和联合支撑集,直至所有非零元素被找出;最后通过反稀疏变换恢复原信号。该算法的具体实现步骤可参考文献[19],在此不再赘述。
3 实验结果与分析
3.1 实验环境设置
(8)
其中均方误差(mean square error,MSE)的表达式如下:
(9)
SSIM的定义为:
(10)
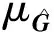
3.2 结果与分析
本文实验使用的图像大小为255×255,首先将煤矿井下图像按列划分为255个255×1的列向量,对每个列向量使用确定性稀疏测量矩阵非线性投影,在恢复信号时,比较CS和DCS的效果,CS使用正交匹配追踪算法(orthogonal matching pursuit,OMP)恢复信号,DCS使用SOMP对3个列向量联合恢复。
对煤矿井下四幅典型图像(图2)进行实验分析,当采样数为160,每个列向量的稀疏度为30、联合稀疏度为60时,使用CS和DCS恢复图像,效果如图3、图4所示。可见,DCS方法比CS方法恢复图像质量更好,具有更高的PSNR值和SSIM值。

图2 煤矿井下原始图像
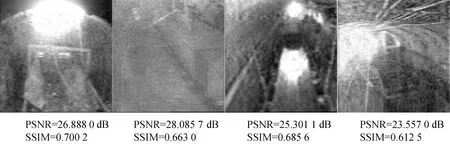
图3 CS恢复的图像

图4 DCS恢复的图像
对100幅煤矿井下图像进行实验,恢复结果的平均PSNR值如图5所示,平均SSIM值如图6所示。可见,随着测量数增加,非线性投影获得的图像信息量逐渐增多,恢复图像的PSNR值和SSIM值逐步提高;同时,在任一测量数时,DCS方法恢复图像的质量都高于CS方法,这与DCS不仅能够利用信号内相关性还能利用信号间相关性,而CS仅仅利用了信号内相关性的理论是一致的。
煤矿安全生产对数据实时性要求较高,因此我们比较了CS和DCS恢复图像所需的时间,如图7所示。显然,DCS算法恢复图像所需的时间更少,具有更强的实时性,这是由于DCS方法采用了联合稀疏模型,利用信号间相关性对非零元素位置进行联合查找,减少了算法迭代次数。
图5 煤矿井下图像PSNR值随测量数的变化情况
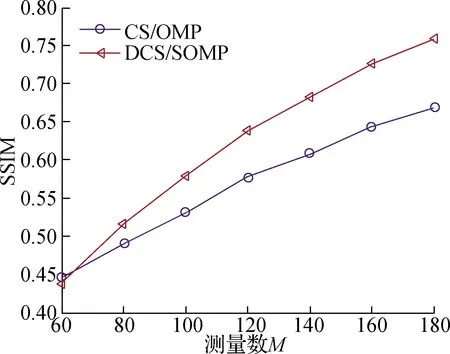
图6 煤矿井下图像SSIM值随测量数的变化情况
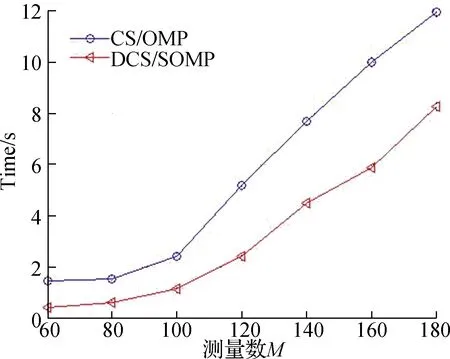
图7 恢复图像所需时间随测量数的变化情况
4 结 语
针对煤矿无线传感器网络能量、计算资源受限的问题,本文提出了基于分布式压缩感知的煤矿井下图像压缩采集方法,将图像按列划分为多个图像块,对每个图像块单独压缩编码并在服务器联合解码。实验结果表明,本文方法应用于煤矿井下图像压缩采集时,比压缩感知恢复的图像质量更高,具有更高的PSNR值和SSIM值。另外,本文算法通过联合查找非零元素位置恢复图像,恢复图像所需的时间比压缩感知算法更少,实时性更强。

