面向人机交互的复杂产品数字孪生装配模型
李 娟
(金陵科技学院计算机工程学院,江苏 南京 211169)
复杂产品指的是采用高端技术、通过复杂的生产工艺加工制造完成的产品,该类产品包含的零件数量极多,各个零部件之间、零部件与产品之间存在明显的变化关联[1],并且该类产品的结构层次复杂、价值较高,如大型通信产品、航空航天产品、大型武器及大型船舶等。该类产品具备多种显著特点,如技术复杂、制造流程复杂、管理复杂、维护复杂等[2]。智能装配是复杂产品的主要装配方式,可以保证复杂产品具备极高的服役性、可靠性和保持性,保证产品各个零部件在装配过程中的性能和精度,以此确保产品的高装配质量[3]。数字孪生作为一种理论技术体系,在产品设计、制造等领域均被广泛应用。数字孪生以物理模型、历史数据为基础,实现多物理量、多尺度以及多概率的仿真,同时在虚拟空间内完成映射,可体现产品在全生命周期内的所有状态。数字孪生在应用过程中,可结合人机交互实现可视化显示,为装配管理和控制提供直观结果[4]。
当下复杂产品在装配过程中具备离散性,这对产品的最终质量造成影响。白朝阳等[5]和白仲航等[6]针对复杂产品的装配需求和现状进行分析,考虑批量分割因素,构建了基于设计任务的相关模型,用于完成复杂产品的装配管理。Il等[7]提出多人产品装配线平衡问题的约束规划模型,旨在开发一种有效的精确解方法(即约束规划),通过将周期时间最小化和工人总数最小化分别作为主要目标和次要目标,提出了两个混合整数线性规划模型来优化求解问题。虽然上述方法能够完成复杂产品的相应管理,但是对于管理的可视化缺少进一步的研究。本文对复杂产品的装配过程进行充分分析,以实现人机交互为基础,研究复杂产品的数字孪生装配模型,对复杂产品装配过程实行管理,控制装配质量。
1 基于数字孪生的复杂产品装配模型
1.1 基于数字孪生的复杂产品装配管理模型
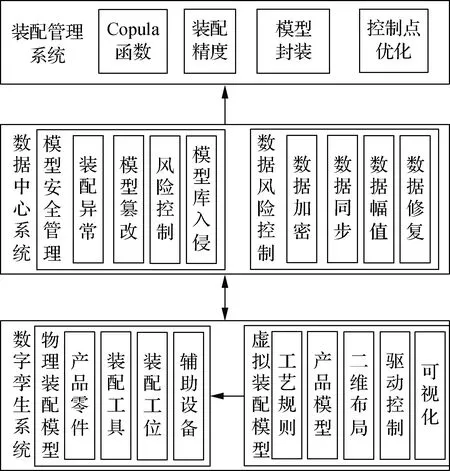
图1 基于数字孪生的复杂产品装配管理模型
本文构建基于数字孪生的复杂产品装配管理模型,模型共包含三个部分:数字孪生系统是复杂产品装配管理模型的基础模块,数据中心系统是模型的核心模块,装配管理系统是模型的控制模块。三者共同构成复杂产品装配管理模型,具体结构如图1所示。
1)数字孪生系统。该系统包含物理和虚拟两种产品装配模型,前者是复杂产品的物理装配空间,其中包含产品装配所需的零件、物品、相关设备等;后者是以前者为参照构建的函数模型,由装配工艺规则、产品模型、二维布局等组成。物理和虚拟两种模型之间存在相互映射的关系,虚拟模型能够实时控制和驱动物理模型的运行。虚拟模型在运行过程中,利用数字孪生AR技术可以完成复杂产品装配管理模型信息的可视化。
2)数据中心系统。数字孪生系统在应用过程中会产生与复杂产品装配相关的大量的、多物理量、多尺度以及多源异构的数据[8],模型在构建过程中需调用这些数据,该过程存在一定的安全隐患。因此数据中心对模型和数据实行独立管理,采用风险控制模型对复杂产品装配模型进行安全管理,采用数据加密技术完成对数据的风险控制;并且数据中心能够对数据进行隔离分类存储,保证数据的访问和存储安全,同时对于价值极高的数据,实行数据同步、复制处理,完成数据备份和修复等。
3)装配管理系统。装配管理的主要作用是实现复杂产品的装配管理和质量控制,通过多种软件完成复杂产品的数据分析、管理以及装配质量控制[9]。
1.2 基于数字孪生AR技术的复杂产品多视图动态生成
基于数字孪生的复杂产品装配管理模型中的数据存在明显的多样性和复杂性,模型在产品装配过程中,需调用不同的产品数据。为了保证装配模型在生成过程中能够自主选择相关的装配数据,形成相关模型界面,极大程度提升用户对有效信息的获取效率,提升装配速度[10],数字孪生系统采用数字孪生AR技术完成装配模型的多视图动态生成。
复杂产品的加工工序用Pi表示,锚点用A表示,可视化对象变换矩阵用M表示,装配模型构建过程中可完成相应数据的自动转换,使其形成可视化对象,采用三维模型对装配所需工具进行描述[11],模型的静态和动态两种信息分别通过文本方式和图表方式表达。将模型中的关联对象和物理对象融合得出A,对比理想的装配画面和当下模型视图得出M,在此基础上将复杂产品和A实行绑定,以M为依据完成可视图的调整,生成复杂产品装配的AR视图。
所有AR视图中的对象均存在变化,该变化直接受到产品的装配工序或者装配情况的影响[12]。设Re、Se、Fe均表示视图对象,依次对应动态选择、人工选择和固有状态的视图对象,三者分别依据控制界面、加工界面和当下装配状态完成,将三者进行组合后,形成AR多视图V,其公式为:
V⊆(Re,Se,Fe)
(1)
本文用Ui表示AR视图对象,其与Re的推荐结果存在直接关联;C和P分别表示模型的状态信息和工序,前者对应模型的上下文,两者之间存在相互关联。忽略C对模型视图数据选择的影响,在复杂产品装配工序P内υ表示特定视图,评分用rυ,p表示;将C与其他完成计算的工序视图Pυ的评分进行对比,并对Pυ的评分进行加权处理,将处理后的结果作为预测依据。如果经过评分处理后的视图用Pυ描述,那么υ的平均评分计算公式为:
(2)
式中:ψ表示装配状态转移系数;υ的评分分为两种,分别基于相似工序和特定工序完成,以前者对后者的预测为基础,采用协作过滤算法完成评分,同时再用皮尔逊相关系数计算各个复杂产品装配工序之间的相关性。ω(p,a)表示相关性,计算公式为:
(3)
式中:IP和Ia均表示装配模型集合。
任意两个工序之间的相似度的衡量可通过ω(p,a)描述,ω(p,a)越高,绝对值越高。ω(p,a)的取值范围为[-1,1]。基于上述内容,即可获取复杂产品装配任意工序P中υ的推荐评分,计算公式为:
(4)
(5)
式中:k为因子,可用于描述标准化权重。
数据融合过程中,C=(C1,C2,…,Ck)表示上下文模型装配信息及其位于某维度上可属于任一装配类别。为获取上下文关系和装配模型的视图关联度矩阵,采用灰色关联度算法求解得出:
(6)
则复杂产品装配模型的视图对象计算公式为:
p=C×rmn
(7)
通过上述步骤即可依据需求完成评分的计算和排列,且按照由大到小的顺序将前N名的视图作为固定视图,用户选择视图对象后,形成AR多视图。
1.3 复杂产品装配过程质量控制优化方法
装配管理系统是对复杂产品的装配实行控制和管理的主要系统。复杂产品在装配时,需在产品装配的AR多视图中,设定质量控制点,该控制点的主要作用是保证装配工艺的规范性,以确保装配的最终质量[13]。为了提升质量控制点的控制效果,针对装配质量的控制优化展开研究,提出基于Copula函数的装配过程质量优化方法。
该方法在控制优化过程中,需构建相关性模型和采用Copula函数,描述每一个控制点之间的关联性。设装配工序为Si,Si∈{S1,S2,…,Sn}表示规定工序以Si为依据完成复杂产品的装配;α={α1,α2,…,αj,…,αm}表示Si的质量控制点,数量为m。
依据装配标准对αi实行划分,使其形成数量为k的控制阀,并按照升序方式实行排列,为[ui0,ui1),[ui1,ui2),…,[ui,k-1,uik);αij表示[ui,j-1,uij),其中j=1,2,…,k;k值会受到装配工具的精度、装配技术等多种因素影响,精度和技术越好,k值越大。针对复杂产品装配时前后两个质量控制点之间存在的关联影响,采用合理的控制阀提升复杂产品的装配质量[14]。
用f(xi)表示αi对应的概率密度函数,则αi的概率分布计算公式为:
(8)
式中:a和A均表示常数,对应质量控制点;S表示定义域,对应Xi;H(Xi)表示概率分布的估计结果,不存在偏差;xi表示变量;ζ表示控制效果影响因数。控制点之间的相关性程度可采用公式(9)描述:
(9)
I(Xi;Xi-1)=I(Xi)-I(Xi|Xi-1)
(10)
式中:信息量用I(Xi;Xi-1)表示,为共享;I(Xi|Xi-1)描述不确定程度,对应两个相邻的控制点。因此,αi-1的质量控制优化需依据αi的质量控制点的装配结果来完成。
αi的装配质量不确定程度为I(Xi),结合αi-1处的装配信息后[15],装配质量的不确定程度用I(Xi|Xi-1)描述。在上述内容的基础上,完成稳定性指数测定模型的构建,属于复杂产品装配,公式为:
(11)
R(αi|x∈αi)=1-ζ[I(Xi|Xi-1)/H(Xi)]
(12)
式中:αij表示控制阀,αj装配的成功率用P(αj|x∈αj)表示;R(αi|x∈αi)表示αi装配的比例,该值越大,表示装配越不稳定,反之则表示越稳定。
2 实验结果与分析
为测试本文模型的应用效果,以我国某船舶制造车间为例,进行相关测试。船舶产品结构复杂,在装配过程中需要几千种甚至上万种零件,结构零件的装配质量和产生的偏差源之间具备非线性、多层级耦合以及不确定性。该生产车间共有12个加工工位、12台数控机床、14个边线库以及夹具、刀具等辅助设备。本文采用Microsoft Net Framework AJAX技术,结合Microsoft Visual Studio软件,完成仿真测试,构建基于数字孪生的复杂产品装配模型。
本文模型的构建主要是为了全面掌控船舶产品装配过程,保证产品的装配质量。因此,模型需全面体现船舶装配信息,实现人机交互。为了测试本文模型的可视化效果,依据船舶生产实际数据的类别完成本文模型的AR动态图生成,结果如图2所示。分析图2可得:本文模型能够依据船舶产品实体的物理结构,动态生成其装配多视图,并且视图效果清晰。
为衡量本文生成的AR动态图效果,选取24种AR动态图并进行评分,如图3所示。分析图3可得:选取的24种AR视图的评分结果存在一定差异,但均在0.90以上,高于国标的期望值0.88,表明本文模型生成的AR视图效果良好。
为测试本文模型在船舶产品装配过程中的人机交互效果,获取本文模型在调整选择视图对象、装配控制、选择工位和工具以及统计装配质量等多种交互情况时的结果,随机抽取图4、图5的结果进行呈现。分析图4、图5可得:本文模型能够呈现装配空间各个工位的情况,点击不同的工位即可呈现对应工位的结果,展示该工位的装配情况等,并能够完成不同视图界面的切换,呈现装配进度、装配工具等结果;同时可查看发生装配质量问题的详细结果,执行相应的操作处理。因此,本文模型具备良好的人机交互效果。

(a)实体物理结构

(b)生成的装配多视图图2 本文模型的AR动态图生成结果
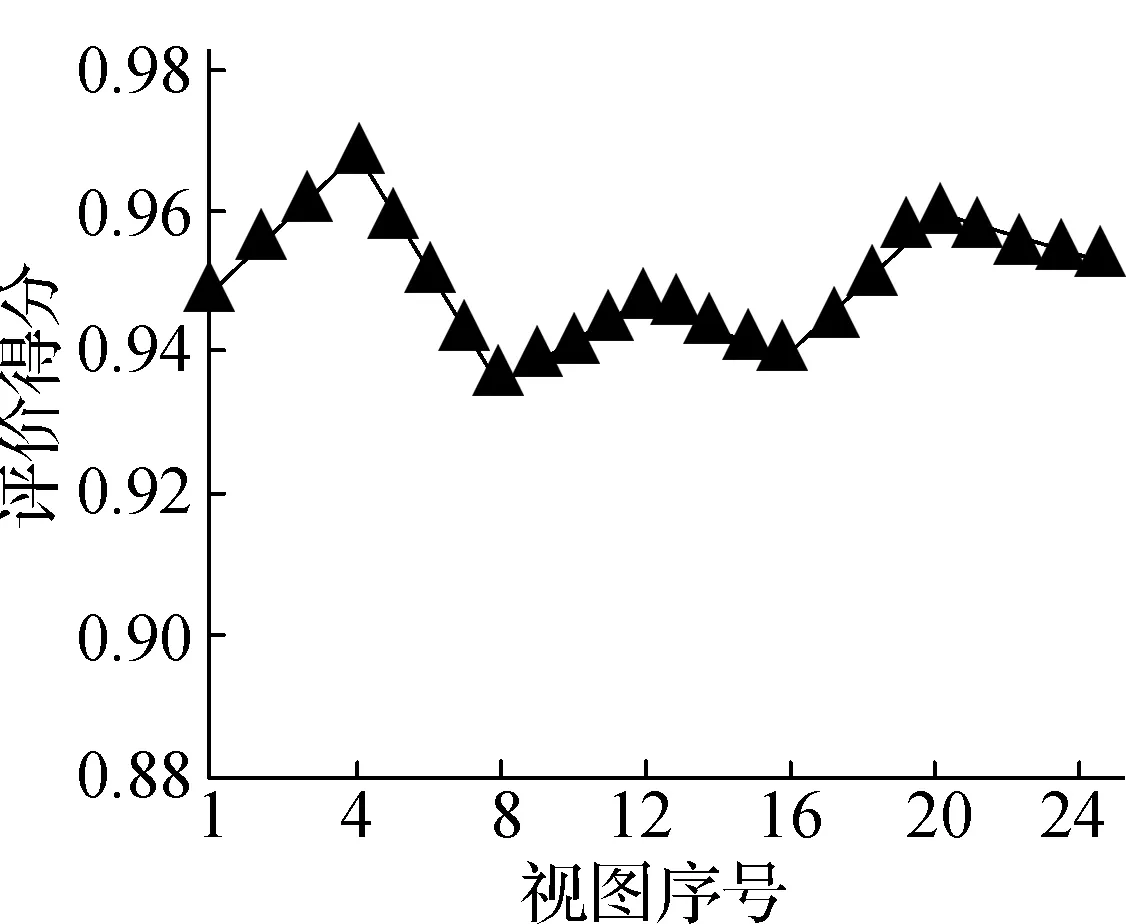
图3 多视图效果测试结果
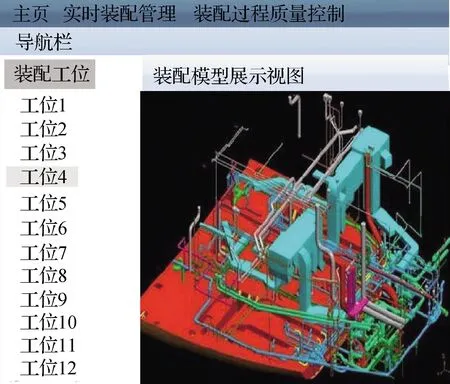
图4 工位和工具选择交互界面
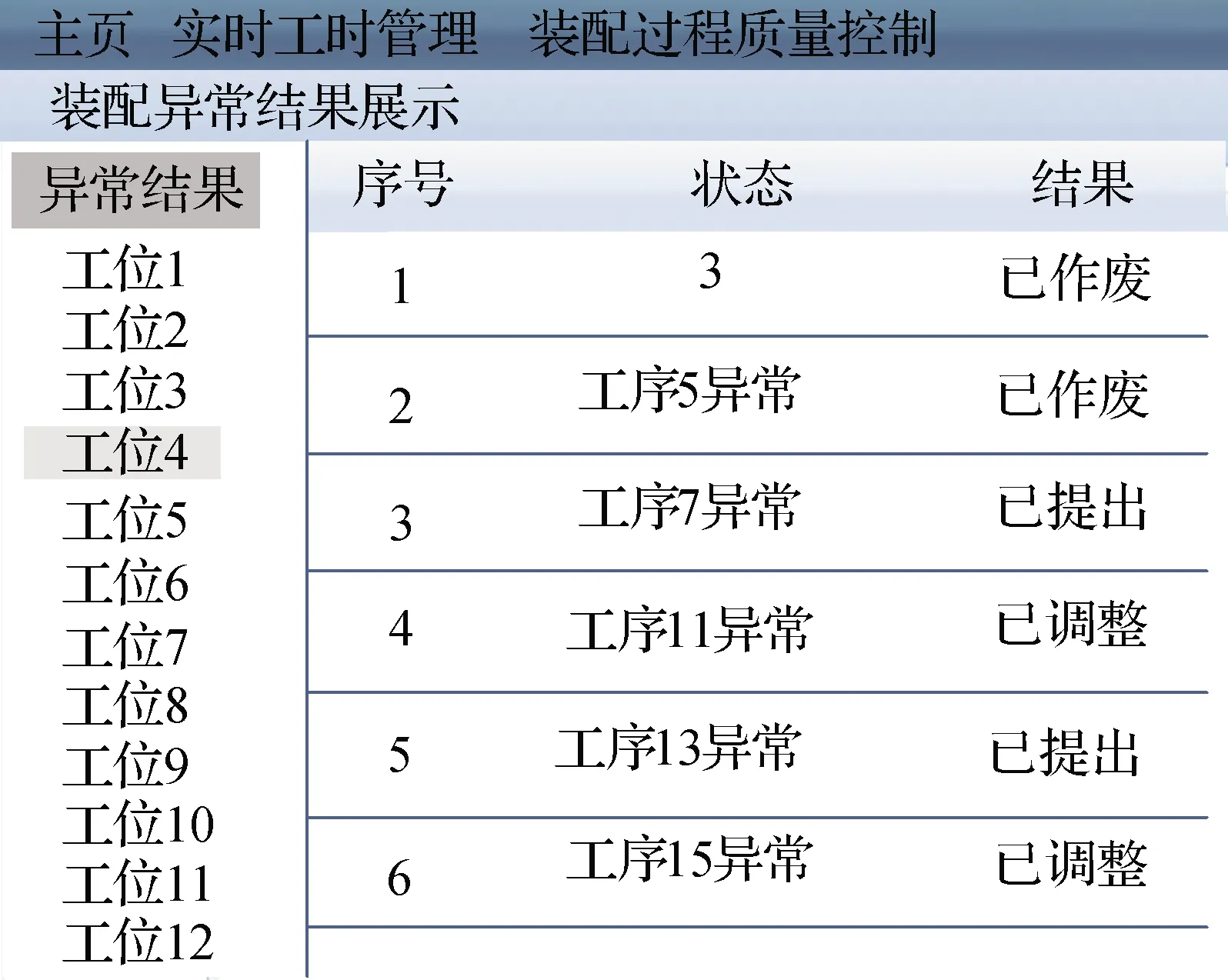
图5 装配质量统计结果交互界面
为测试本文模型对于船舶产品装配质量的实时管控性能,采用绝对值质量离差作为评价标准,公式如下:
Δ=dist(X,Y)=|xi-x0|
(13)
(14)
{Δm∈Δ|Δ>(max+min)/2}
(15)
式中:xi表示装配质量数据;x0表示平均值,对应装配规范质量数据区间;Δ表示绝对质量离差;δ表示相对质量离差;Δm表示大于二分之一区间长度的绝对质量离差;max和min分别表示装配规范质量数据取值标准的最大值和最小值。
获取本文模型不同控制点船舶产品装配效果的绝对值质量离差,随机抽取其中8个,结果如表1所示。
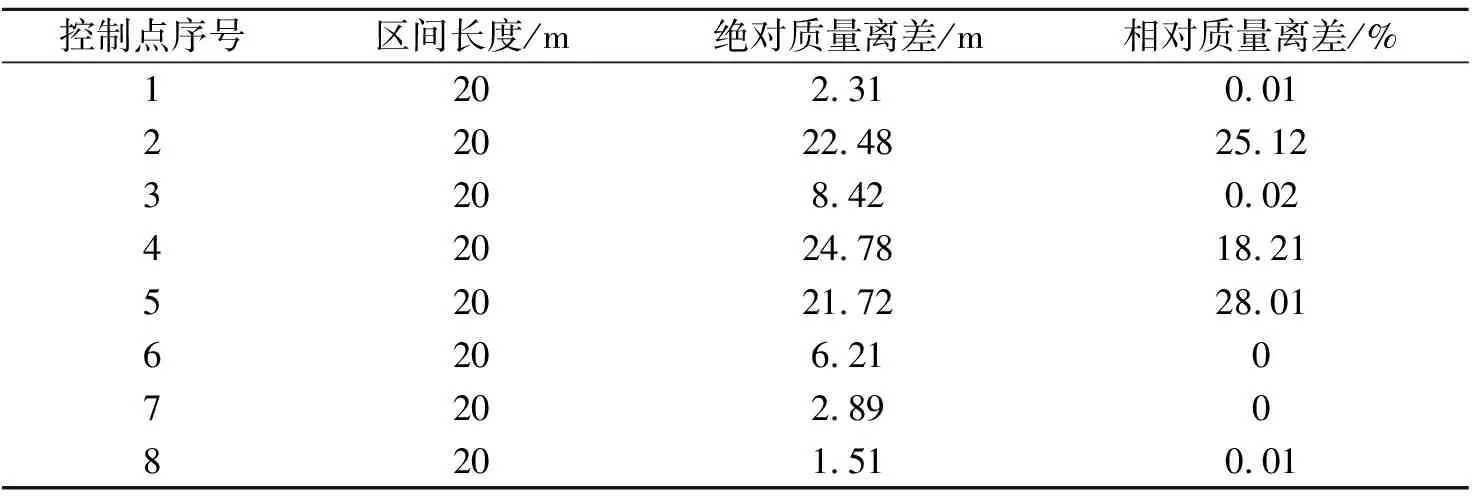
表1 产品装配效果的质量离差结果
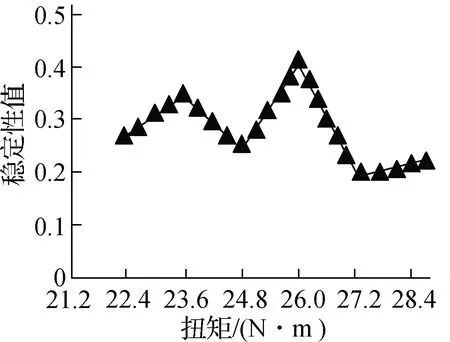
图6 质量控制的稳定性值
分析表1可得:随机选取的8个质量控制点的绝对质量离差和相对质量离差存在差异,其中控制点2、4、5的两种误差结果大于区间长度的二分之一,表示这些控制点的装配质量符合标准要求。该结果表明本文模型能够实现船舶产品装配的实时管控。
获取本文模型在不同大小螺栓扭矩下质量控制的稳定性值(图6)以衡量本文模型对船舶产品的装配质量控制效果,其中螺栓扭矩为随机获取,根据国标要求其稳定性值应低于0.5。
分析图6可得:在不同的螺栓扭矩下,本文模型的质量控制稳定性值均低于0.45,表示本文模型能够较好地控制船舶产品装配质量。
3 结 语
复杂产品的装配过程对于产品的最终质量存在直接影响。为全程管理和控制复杂产品的装配情况,实现装配结果的可视化,本文研究面向人机交互的复杂产品数字孪生装配模型,全面管控复杂产品装配过程,保证装配质量。测试结果显示:本文模型能够很好地完成复杂产品装配的实时管控,可呈现装配的整体情况,生成AR多视图动态,能够很好地实现复杂产品装配质量的控制。

