基于计算模型修正的直剪试验分析

董彬林

(青海省兴利公路桥梁工程有限公司 西宁 810000)

0 引 言

在岩土工程领域，土体的力学性质(如应力-应变关系、抗剪强度参数等)是工程调查与设计的重要依据，也是地(路)基承载力计算、边坡稳定性评价的关键。因此，快速、准确地确定土体的力学性质对岩土工程研究意义重大。

目前，研究土体抗剪强度参数的试验方法有很多，如三轴试验、无侧限抗压强度试验、直剪试验等。其中，直剪试验的操作计算简单，可以快速获得土体的抗剪强度参数，被广泛应用于科学研究和工程实际，但直剪试验自身却存在一些缺陷，传统计算方法将剪切面积视为定值，虽然简化了计算过程，却忽视了剪切过程中剪切面积的变化，而剪切应力、抗剪强度参数的计算皆与剪切面积有关，因此，依据传统方法计算的结果将难以准确反映材料的真实力学性能。

许多学者相继提出了有效剪切面积、应力的计算方法。王伟[1]对剪切面积进行积分计算，得到了有效剪切面与剪切应力的计算公式，发现当剪切位移达到4 mm时，剪切应力实验值与修正值之间的误差将达到10%左右。詹金林等[2]研究了圆盒直径与剪切应力计算误差的关系，提出一种将试样盒做成上盒小下盒大的方式，来降低剪切面积减小所带来的误差。徐志伟等[3]采取压力除以有效面积计算方法，实现对剪切面正应力的修正，认为在剪切应力计算时应考虑剪切面积的变化，在抗剪强度计算时可以忽略面积的变化。葛云峰等[4]研究了考虑剪切面积变化的岩体结构面应力与强度参数的变化规律。余凯等[5]总结了单点面积修正方法与多点面积修正方法，在此基础上提出了基于面积修正和正应力修正的单点面积应力修正方法，同样发现剪切位移的增加会使得剪切应力大于实测值。董云等[6]考虑剪切过程中，正应力偏心引起的剪切面起伏，借助波形剪切面计算模型对有效剪切面积进行了修正，指出该计算模型的计算结果更加接近土样强度真实值，但剪切面的起伏特征却很难获取，难以在实际应用中实现。张亮亮等[7]推导了有效剪切面积计算公式，采用最小二乘法对数据进行处理，发现土体抗剪强度误差随环刀面积的增加而减少，基于剪切面积修正的结果表明抗剪强度参数的真实值大于实测值。

综上所述，众多学者在剪切面积变化会影响剪切应力与正应力问题上已基本达成共识[8-12]，但因为对直剪试验计算模型的简化不同，致使有效剪切面积与有效应力的计算模型多样，对剪切试验的结果分析也存在一定的差异。而且，多数研究是针对标准直剪试验，其计算结果难以推广到非标(任意半径)试验。因此，本文通过解析公式推导出考虑有效剪切面积的直剪试验计算模型，给出剪切面积、剪切应力、正应力的普适修正计算模型，结合多因素影响下粉质黏土的直剪试验数据，研究修正模型对剪切应力-剪切位移关系以及抗剪强度参数的影响，在直剪试验修正模型与摩尔-库伦准则基础上，建立了基于有效剪切面积计算的剪切强度准则。

1 计算模型修正

1.1 剪切面积修正

剪切过程中，上下剪切盒产生相对位移，剪切面积减小，计算简图如图1所示，当剪切位移为s时，根据对称性，可先计算1/4的剪切面积A/4。

扇形面积：

(1)

三角形面积：

(2)

修正剪切面积：

A=4(As-Ar)=πr2-2r2θ0-r2sin2θ0

(3)

其中：

(4)

修正后剪切面积的绝对误差δA与相对误差δA’分别为：

δA=A-A0=(-2θ0-sin2θ0)r2

(5)

(6)

A=A0(1+δA’)

(7)

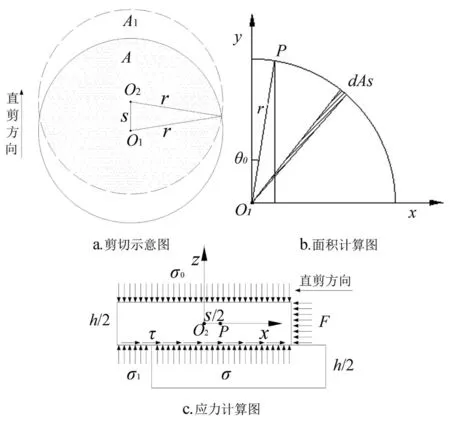
图1 直剪试验计算模型

在式(7)中，δA’也可以被视为剪切面积修正系数。图2为根据圆形直剪盒尺寸经归一化处理，得到的修正前后剪切面积的相对误差与相对剪切位移之间的关系。如图2a整体关系图所示：相对误差与相对剪切位移之间是非线性关系，且相对误差始终为负值，表示在剪切过程中，随着剪切位移的增大，有效剪切面积不断减小。事实上，对于标准直剪试验，剪切盒直径为61.8mm，剪切位移一般在0～6mm范围内，所以应重点研究δA’在相对剪切位移0～0.1区间内的变化。如图2b局部图所示：相对剪切位移在0～0.1区间内时，δA’与相对剪切位移具有良好的线性关系。

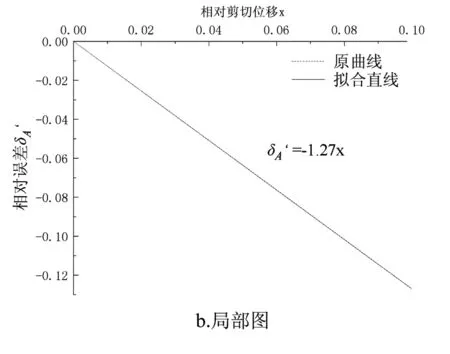
图2 剪切面积绝对误差与相对剪切位移关系

1.2 剪切应力修正

传统方法将百分表位移计示数与量力环的劲度系数相乘以表示剪切应力，即剪切应力实测值，而剪切应力表示的是单位面积的受荷情况，即为剪切应力真实值。由式(3)和式(4)可以看出有效剪切面积是剪切位移与直剪盒尺寸的函数，会随相对剪切位移的增加而减小，因此，按照传统方法计算得出的剪切应力实测值与真实值直剪存在误差，需要对原计算模型进行修正，即：

(8)

(9)

上式中：C为量力环的劲度系数，R为百分表示数，CR表示量力环劲度系数与示数的乘积，β1为剪切应力修正系数。由式(9)与式(4)可以看出β1同样是关于剪切位移与直剪盒尺寸两个变量的函数，单纯研究剪切位移与β1的关系不具有普遍适用性。现对剪切位移与直剪盒尺寸做归一化处理，得到β1与相对剪切位移的关系如图3所示，在0～0.1区间内，β1的增量与相对剪切位移的增量大体成正比，当相对剪切位移达到0.1时，其剪切应力差值将达到14.6%。

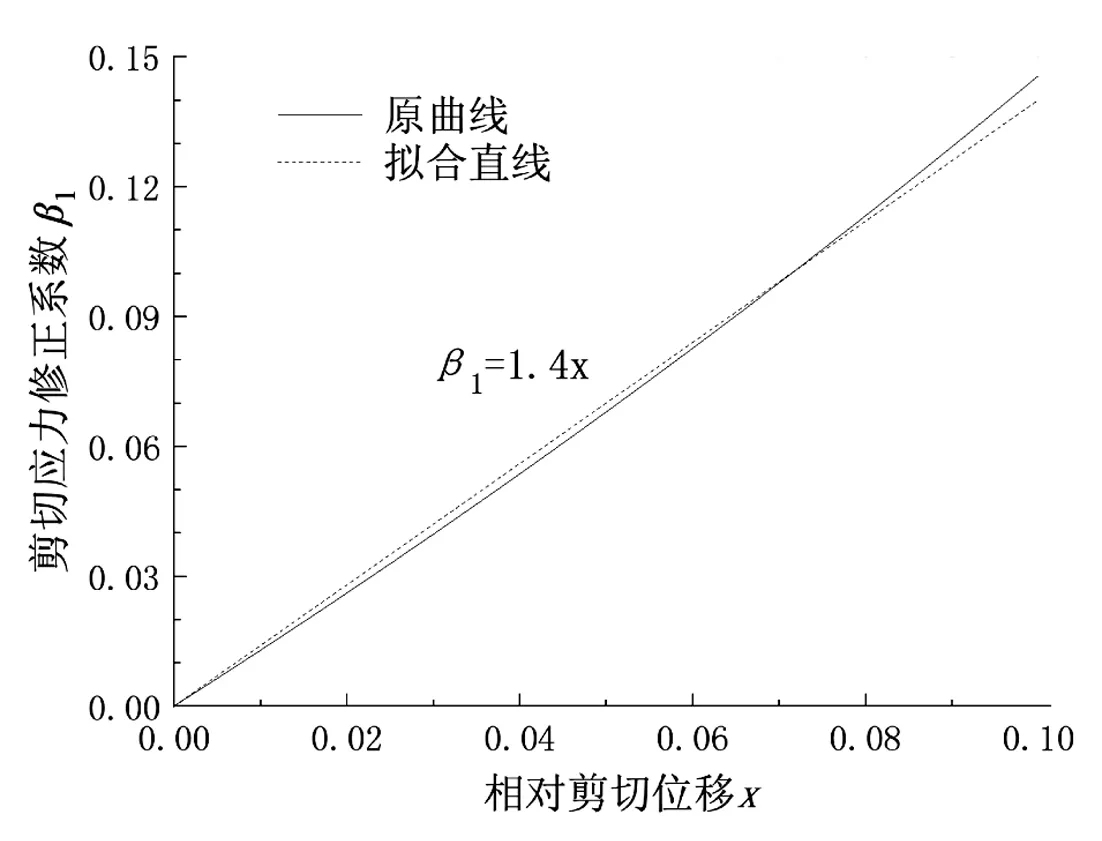
图3 剪切应力修正系数与相对剪切位移关系

1.3 正应力修正

由于剪切过程中，有效剪切面积减小，法向压力未曾变化，其剪切面上的正应力分布必然发生改变。假定σ0为法向应力，σ1为下剪切盒施加的应力，σ为剪切面上的真实正应力，h为直剪试样的厚度，由力的平衡关系可得：

(10)

(11)

上式中：A0为圆的面积，xP为σ1的等效力与O2点的距离，由形心计算可得：

(12)

联立式(10-12)可得修正应力σ为：

(13)

(14)

上式中：β2为正应力修正系数，也是关于剪切位移与直剪盒尺寸两个变量的函数，同样对其进行归一化处理，得到β2与相对剪切位移的关系如图4所示。可以发现β2与β1具有相似的变化规律，皆随相对剪切位移的增加而增大，且增速不断加快，在0～0.1区间内，β2的增量与相对剪切位移的增量同样表现出正相关性，当相对剪切位移达到10%时，其正应力修正系数达到23.55%，β2与剪切应力的乘积也将随之扩大，反映出正应力真实值与实测值直剪的差值随剪切位移的增加而逐步增大。

图4 正应力修正系数与相对剪切位移关系

2 直剪试验结果分析

基于上述修正计算模型，本文对参考文献[13]的直剪试验结果加以对比。

2.1 剪切应力-位移关系

以最优含水率16.7%、最大干密度1.67 g/cm3、冻融循环0次的粉质黏土直剪试验结果为例，其修正前后剪切应力-剪切位移关系(以下简称τ-μ曲线)如图5所示，当法向应力为0 kPa，50 kPa，100 kPa时，τ-μ曲线存在剪切应力峰值，为应变软化型；当法向应力为200 kPa时，τ-μ曲线无峰值应力，为应变硬化型，修正前后不会改变τ-μ曲线类型。法向应力为0 kPa时，修正前后τ-μ曲线几乎重合，法向应力为50 kPa、100 kPa、200 kPa时，对应的最大剪应力差值分别为-5.567 kPa、-9.948 kPa、-17.97 kPa，再次证实了剪切应力实测值小于真实值，而二者间的误差与法向应力有关，法向应力值越大，误差越大。

2.2 抗剪强度参数

基于摩尔-库伦准则与修正计算模型，计算得出修正后的抗剪强度参数内摩擦角φ、黏聚力C，得到修正前后抗剪强度参数的相对误差如图6所示，其计算公式如式(15)：

(15)

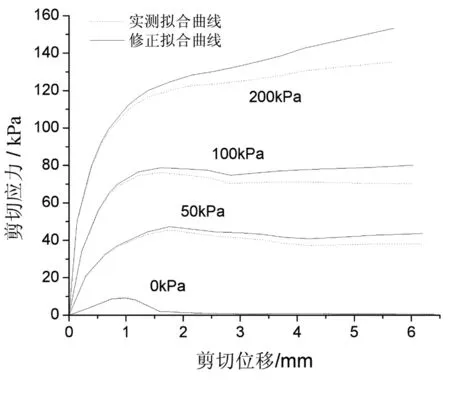
图5 剪切应力与剪切位移关系

计算得出修正前后的抗剪强度参数多为负值，即抗剪强度参数的实测值比真实值偏大。其中，内摩擦角的相对误差最大为0.008，最小为-0.033，平均值为-0.008；黏聚力的相对误差最大值为0.060，最小值为-0.303，平均值为-0.099，可见修正模型对于内摩擦角与黏聚力计算结果的影响程度不同。其中，摩擦角的相对误差具有良好的集聚性，修正前后摩擦角变化在1%左右，反应出剪切面积的变化对摩擦角的影响较小；黏聚力的相对误差具有较高的离散性，修正前后黏聚力变化很大，最大误差超过30%，反映出剪切面积的变化对粘聚力影响十分显著。

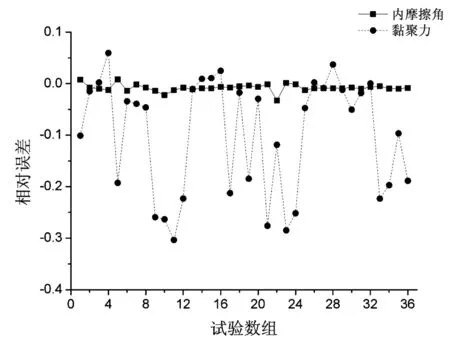
图6 抗剪强度参数相对误差

3 结 语

本文在前人研究基础上，推导了直剪试验的修正计算模型，对修正前后的直剪试验结果加以分析，得出的主要结论如下：

(1)传统方法虽然计算简单，但忽视了剪切过程中剪切面积变化引起的剪切应力与正应力变化，根据修正后计算模型，分析得出由于剪切过程中剪切面积减小，剪切应力、正应力的实测值均低于二者修正后的真实值，实测值与真实值的误差会随相对剪切位移的增加而增大。

(2)基于修正模型对前人的直剪试验结果对比发现，修正前后并不会改变对土体破坏类型的判断，修正前后的剪切强度与法向应力有关，法向应力越大，则二者的差值也越大。

(3)摩尔-库伦准则对修正前后的直剪试验数据均具有良好的适用性，修正前后内摩擦角的变化幅度微小，可近似忽略，但黏聚力的变化离散性高，修正模型对粘聚力影响显著。