基于SkipList的ORE算法的改进与实现

姚李昊升，杨立新，张于洁，蒋 欣

（1.长江大学 电子信息学院，湖北 荆州 434020；2.湖北省科技信息研究院，武汉 430071；3.武汉理工大学 计算机与人工智能学院，武汉 430070）

引言

现有的云存储服务为用户提供了方便的数据存储、管理和共享服务，云计算技术开放式存储及应用为用户带来便捷[1]。同时，云存储服务也逐渐面临着越来越多的安全问题。云上层出不穷的数据泄露问题，各种各样的黑客攻击事件，给云存储服务带来了前所未有的挑战。用户认为云服务器通常是不完全可信的，因此存储在云上的数据有必要通过加密进行保护，然而在对数据进行加密的同时，使得一些在明文空间上的函数计算不再适用于密文空间，例如区间查询。

区间查询[2]-[3]是对数据进行查询的主要方式之一。在明文区间查询中，用户向服务器提供查询区间，然后服务器将关键字在查询区间内的所有数据反馈给用户。但是在密文区间查询中，为保证敏感数据的机密性，用户需要将加密后的查询区间陷门发送给服务器，服务器运行查询算法后将符合条件的密文反馈给用户，由私钥解密后得到相应的明文数据。由于查询需要在密文状态下进行，因此如何在保证安全性的同时实现高效查询是目前主要难点。

早期国内外相关学者在密文区间查询上研究保序加密方案（Order Preserving Encryption，OPE）对关键字查询的可行性。由于该方案的明文和密文具有相同的一致性顺序关系，因此容易遭受统计性攻击，导致方案的安全性较低。已有文献[4]构造了一种非线性的OPE方案，该方案不需要已知原始明文的分布规律、数据量的大小等信息，在安全性上面得到了很大的加强。但是此方案基于的假设是数据特征会随着时间的变化而变化，因此不具有实用性。在OPE 方案的基础上，也有文献[5]提出了顺序揭示加密方案（Order Revealing Encryption，ORE）。ORE方案的构造依赖于多重线性映射函数，所支持的区间查询数据类型不仅仅只包括数值型数据，还包括其他类型的数据。Lewi等人在传统ORE方案的基础上提出了一种能够抵抗推断攻击的改进的ORE方案（Left-Right Order Revealing Encryption，LRORE）[6]，该方案可以保证泄露更少的顺序信息，由此更好地保护数据的安全，但此方案的数据组织结构采用顺序存储，对于数据的插入和删除操作，会造成大量的数据移动，产生很大的时间开销。

针对LRORE方案数据存储结构的不足，提出一种基于跳跃表（SkipList）的存储结构的顺序揭示加密方案（SL-ORE），在保证安全性的前提下，提升了数据插入和删除的效率，使其能够保持和密文查询时相同的时间复杂度。

1 相关研究

常见的密文区间查询主要有以下几种方案：

1.1 OPE方案

云服务器可以根据密文的顺序信息来得到明文顺序信息，因此，OPE方案可以保证涉及顺序信息的查询操作可以在密文空间高效进行。当进行区间查询时，用户只需要提供查询区间两个端点的密文给云服务器。随后，云服务器根据用户提供区间端点的加密密文与原有数据库的密文进行比较。最后，云服务器返回给用户符合查询要求的密文数据，用户解密即可。

OPE 方案的最佳理想安全性（Indistinguish Ability Under Ordered Chosen Plaintext Attack，IND-OCPA），最早是由Boldyreva等人[3]提出的，该安全性是保序加密方案的最高理想安全性。

随后Boldyreva等人提出了一种利用随机保序函数和超几何分布设计的可证安全的OPE方案。该方案保证了安全性，即使攻击者得到全部密文，除了密文的顺序以外，就再也得不到其它任何有用的信息。

1.2 ORE方案

有文献指出Boldyreva的OPE方案会泄露明文至少一半的比特信息[7]-[8]，为此Boneh[9]等人在原有OPE方案的基础上提出了顺序揭示加密ORE方案，该方案与保序加密不同，ORE方案是依据一个公开的比较函数来决定两个相应明文的大小，而不是直接比较密文之间的数值大小。ORE方案与OPE方案相比较，Boneh等人提出的ORE方案能达到最佳理想安全性IND-OCPA。随后，Chenette等人[10]使用伪随机函数构造出了一种新的ORE方案。

上述方法具有很高的检索效率，因为方案中用到了伪随机函数。但是，该方案仍然不能达到理想安全性，因为算法泄露了不同数据的第一个不相同比特位。

为了减少Chenette等人方案中信息的泄露问题，Cash等人[11]构造出了一个性质保留哈希函数，并且依据双线性对的理论，构造出了一个新的ORE方案，该方案虽然很好地避免信息泄露问题。但是，相对于只使用对称简单原语的加密方案而言，Cash等人的方案在实际场景中查询效率并不高。Furukawa等人[12]构造第一个有陷门的ORE方案，该方案基本思想是使用两个加密密文比较明文大小时，必须知道一方标签，这一标签是ORE方案中的陷门。在该方案中将密文分成密文c 和标签token 两部分。其中token 为比较标签保存在客户端中。当用户进行区间查询时，只需上传查询区间端点的密文以及对应的比较标签。例如，当查询区间[a ,b] 时，用户需向服务器提交( ca,tokena)和( cb,tokenb)，服务器可以进行比较查询，返回相应密文，用户解密得到所需的查询结果。

1.3 LRORE方案

在Furukawa等人所提出的ORE方案中，当查询区间较多时，会造成数据顺序信息的大规模泄露。对此，Lewi等人构造新的顺序揭示加密LRORE方案，该方案的加密过程中包含两种加密算法，其中左加密算法加密明文之后得到左密文，右加密算法加密明文之后得到右密文，云服务器中存储的只是右密文，其中右密文是语义安全的。当数据使用者进行区间查询时，只需要将左加密算法生成的左密文区间端点对应的密文值发送给云服务器，通过比较函数进行左明文和右明文的大小比较之后，将查询结果返回给用户。这样可以保证泄露更少的顺序信息，由此更好地保护数据的安全性。

2 基础知识

常见的索引分为线性表索引，顺序表索引，链表索引、散列索引和树形索引五类。由于线性搜索的方法如今无法满足现有的用户对于数据搜索的要求，虽然树形索引具有扩展性好，查询和更新效率高等优点，但是由于在进行数据的插入和删除操作时，需要不断进行调整树的结构，增加了性能开销。而链表索引的代表SkipList结构在区间查找效率更高，不仅能保持对数级别的数据查询效率，当进行数据插入和删除时，同样也能保持高效的性能，而且适用于大规模数据的并发访问，多个线程可以安全地并发执行插入、删除、更新和查询操作。与其他有锁机制的数据结构在巨大的压力下相比有优势。[13]

SkipList结构如图1所示，是Willipam Pugh等人[14]提出的一种替代平衡树的概率性数据结构，但是与平衡树（如红黑树）不相同的是，跳表实现是基于一种随机化的算法。其形式表现为有序的链表，其与普通链表最大的区别在于：各节点之间有一些附加的并行指针相连。每一个插入到SkipList的key 首先会被插入到最底层的链表中，接着存储这个key 的节点，会以50%的概率将自己发布到上层中。SkipList的查询、插入、删除操作都能达到很好的性能。SkipList满足的基本特征如下：

（1）一个跳表由两层或者两层以上组成。

（2）跳表的第一层包含所有的元素。

（3）每一层都是一个有序的链表。

（4）如果元素x 出现在第i 层，则所有比i 小的层都包含x。

（5）第i 层的元素通过一个down 指针指向下一层拥有相同值的元素。

（6）top 指针指向最高层的第一个元素。

2.1 SkipList查询

例如在图1中要查询key 为19的结点，从head出发，从高到低的level进行查找，先索引到9这个结点，发现9＜19，继续查找（然后在level==2这层），查找到21这个节点，由于21＞19，所以结点不往前走，而是level由2降低到1然后索引到17这个节点，由于17＜19，所以继续往后，索引到21这个结点，发现21＞19，所以level由1降低到0在结点17上，level==0索引到19，查找完毕。如果在level==0这层没有查找到，那么说明不存在key为19的节点，则查找失败。

图1 SkipList结构

2.2 SkipList插入

插入节点的关键就是找到合适的插入位置，即从所有小于待插入节点key 值的节点中，找出最大的那个节点即可。例如在图1 中要插入key 为17 的结点，先需要查找到12，由于12＜17，而12 的下一个结点19＞17，因而满足条件，创建新结点，并且产生一个在1～MAX_LEVEL 之间的随机level 值作为该结点的level，再调整指针指向。

2.3 SkipList删除

首先查找到指定的结点，若没找到则返回，反之调整指针指向，释放结点空间。本文将优化原有方案的数据存储结构，将SkipList 应用到LRORE 方案中，并提出SL-ORE 方案，通过分析得出该方案相比原有方案的具有较大的性能提升，同时它又保持了原有LRORE 方案抵抗统计攻击的安全优势。

3 SL-ORE方案的设计与实现

3.1 SL-ORE方案概述

SL-ORE方案主要包括如下两个过程：

3.1.1 初始化过程：数据拥有者将明文数据D=( x1,x2,…,xm)组织成SkipList结构，再利用生成的密钥对明文SkipList中的数据进行加密，这样就可以获得密文SkipList。服务器对该密文SkipList进行存储（服务器仅存储右密文），同时记录初始密文结构状态st。

3.1.2 区间查询和更新过程：数据使用者将待查询明文通过密钥sk 加密后得到的左密文发送给服务器，比较函数Compare 对当前状态的密文SkipList进行跳跃查找（形如二分查找），比较对象是接收到的左密文和Skip-List中存储的右密文，然后返回查询结果给客户端，最后更新服务器状态st。

3.2 SL-ORE方案实现

本文提出的改进方案可以描述成一个多元组算法如下所示：

(SLRQ.Setup,SLR Q.Range,SLRQ.Insert,SLRQ.Del ete)

3.2.1 SLRQ.Setup( λ,D )初始化算法：

（1）Client( λ,D )→( sk,ct )，数据拥有者以安全参数λ 作为输入，输出一个密钥LRORE.Set( λ) →sk，然后把明文数据D 组织成SkipList后，对于每个元素x ∈D 通过sk 加密生成右密文ct1。

ct1←LRORE.EncryptR( sk,x )，最后将密文SkipList 发送给服务器，如图2 初始化过程所示，其中原始明文为x，加密后的右密文为。

（2）Server( st )→st，服务器在接收客户端发送给它的密文SkipList后，输出一个初始化状态st。

3.2.2 SLRQ.Range( sk,q,st )区间查询算法：

（1）Client( sk,q=( x,y ))→t，数据使用者输入一个查询q=( x,y )，通过密钥sk 加密后生成令牌t。

t=( Encr yptL( sk,x ),EncryptR( sk,y ))。之后发送给服务器。

（2）Server ( st,t )→R，服务器根据收到的令牌t=( ctx,cty)，通过比较函数Compare 对状态为st 密文SkipList进行搜索，找到最小值和最大值，依次读取最小值和最大值之间的密文值，并将这些值作为结果返回给数据使用者R。

（3）Cli ent( sk,R )→S，数据使用者将收到的返回结果R 通过sk 进行解密得到对应的明文。

3.2.3 SL RQ.Insert( sk,q,st )插入算法：

（1）Clie nt( sk,q=x )→t，数据使用者将待插入的值x 通过密钥sk 加密后生成令牌t。

t=( EncryptL( sk,x ),EncryptR( sk,x ))，发送给服务器。

（2）Server( st,t )→st，服务器收到令牌t=( ct1,ct2)（其中ct1,ct2分别表示左密文和右密文）之后，通过比较函数Compare( ct3,·) 对当前状态为st 的密文SkipList进行搜索得到正确的插入位置，插入完成之后更新服务器中当前的密文状态st 。

3.2.4 SLRQ.Delete( sk,q,st )删除算法：

（1）Client( sk,q=x )→t，数据使用者利用密钥对要删除的值进行加密，得到令牌t，

t=( EncryptL( sk,x ))，后发送给服务器。

（2）Server( st,t )→st'，接收到令牌之后，服务器利用比较函数Compare( ct1,·) 对当前状态为st 的SkipList进行搜索，找到ct2t 的位置，删除之后更新服务器的状态st'。

3.3 SL-ORE查询过程

比较函数Compare 通过接收到客户端发送的左密文与服务器存储的右密文进行比较，在密文SkipList中确定检索区间对应的最小和最大密文值，然后得到其中连续的密文结果R={1 2} ，服务器将查询结果返回客户端进行解密得到原始明文S，如图3所示。

3.4 0SL-ORE插入过程

图4 插入过程图

3.5 SL-ORE删除过程

设定服务器中存储的密文SkipList的初始状态为st。如图2所示，客户端待删除的值q=51，服务器接收客户端发送过来的密文值，其中代表左密文，比较函数Compare 将与当前状态为st 的密文SkipList进行比较，找到对应的正确右密文进行删除并更新此时的密文状态为st' ，如图5所示。

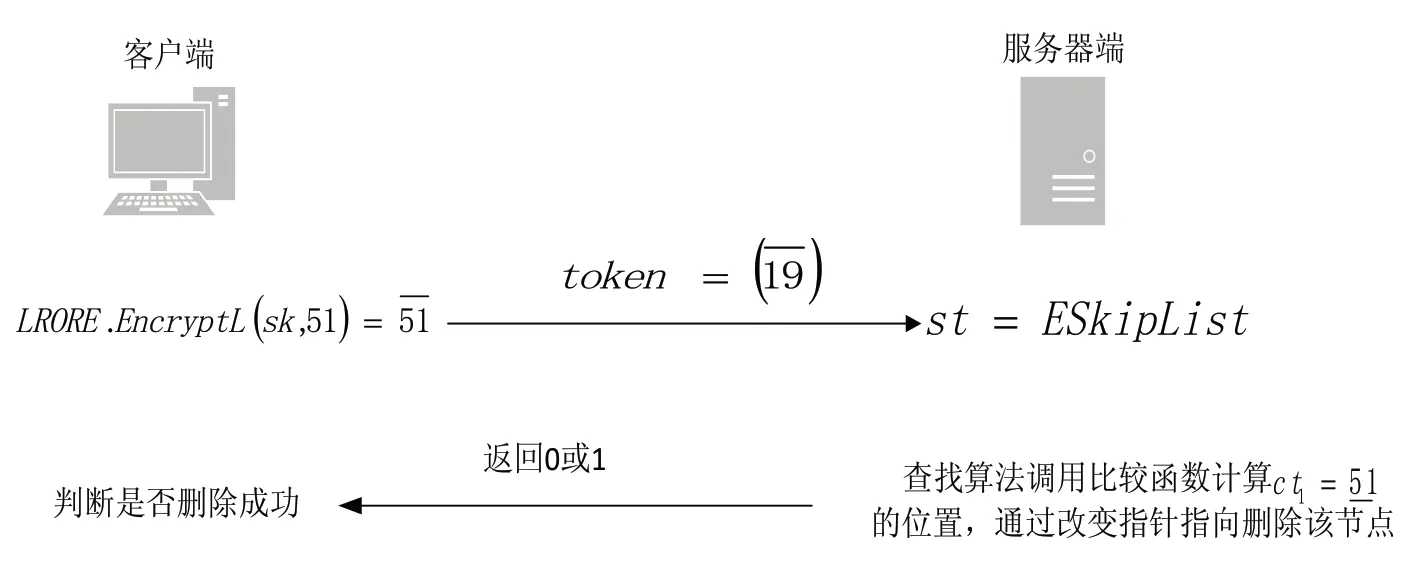
图5 删除过程图

4 安全与性能分析

4.1 性能分析

本文提出的基于SkipList结构的SL-ORE改进方案同Lewi等人的LRORE方案进行了性能的分析比较，在查找过程中，Lewi等人顺序表结构和本文提出的SkipList 结构拥有相同的时间复杂度；但在插入和删除过程中，基于SkipList结构的时间复杂度是对数级别的，具有更好的性能优势，同时还与传统的OPE方法进行对比分析，虽然传统的OPE方案在查询和插入删除的时间复杂度上面和我们所提的SL-ORE方案相同，但是在那种插入、删除频繁的场景中，平衡树需要进行再平衡操作，这会使平衡树的性能急剧下降，此外由于OPE方案的明文和密文具有相同的一致性顺序关系，因此容易遭受统计性攻击，导致它的安全性较低。现将三种方案的查询和插入、删除的时间复杂度进行对比，如表1所示：

表1 时间复杂度对比

SL-ORE方案在提高数据插入和删除的效率方面均优于对比方案。

4.2 安全分析

SL-ORE方案是建立在Lewi等人的LRORE方案基础之上，加密算法分为左加密算法和右加密算法，对应生成左密文和右密文，服务器存储的仅仅是语义安全的右密文，不会受到统计攻击，保留了Lewi原始方案的安全性。

5 结语

本文提出一种新的基于SkipList 的SL-ORE 方案，并阐述了该方案的具体实现过程。通过分析对比所提方案在数据的插入和删除操作上比原有方案耗时更短，并在保留原有安全优势的前提下具有更好的性能优势。