固定效应部分线性变系数面板数据模型的估计

陈 芳，胡二琴

（湖北工业大学 理学院，武汉 430068）

面板数据综合了时间序列和截面数据的特征，成为了统计学和计量经济学分析的热点领域。近二十年来，面板数据的参数（通常是线性）模型分析得到了统计学者热切的关注，并被广泛地应用在实证研究中。参数模型可以简单地描述和分析响应变量与协变量之间的关系，然而它们往往受到模型错误规范的影响，从而导致建模偏差。为了克服这一缺点，非参数和半参数面板数据回归模型近年来引起了计量经济学领域许多研究者的注意。Henderson等[1]和Li 等[2]研究了非参数模型的估计。Baltagi 和Li[3]、Su和Ullah[4]与Zhang等[5]提出了具有固定效应的部分线性面板数据模型。Rodriguez-Poo和Soberon[6]提出了一种基于一阶差分和局部线性回归的变化系数函数估计新技术。赵明涛[7]基于变系数纵向数据模型研究了渐进惩罚估计问题。其中部分线性变系数模型受到了广泛的关注，Seong 和Byeong[8]研究了部分线性变系数模型在系数函数有不同平滑变量时的有效估计。Fan和Huang[9]提出了采用轮廓最小二乘估计法估计部分线性变系数模型，证明了估计量的渐进性质，得出了对于半参数面板数据模型的估计，轮廓最小二乘估计法估计良好的结论。

在前人研究基础上，本文将固定效应引入到部分线性变系数面板数据模型中，通过引入虚拟变量和采用轮廓最小二乘估计法估计模型，最后采用Monte Carlo随机模拟法验证模型的估计效果。

1 模型介绍

本文考虑如下具有固定效应的部分线性变系数面板数据模型

若记

其中In是n维单位矩阵，1T是元素均为1的T维列向量，D 为In与1T的克罗内克积，则模型（1）的矩阵形式为

2 模型的估计

因为模型（1）中αi作为个体固定效应，具有不可观测性，与Xit，Zit具有某种未知的相关结构，在对模型进行估计的过程中要去除αi对Xit，Zit的影响。为了消除αi的影响，在模型（2）两边同乘矩阵W=InT-D(DTD)-1DT，由于WD=D-D(DTD)-1DTD=0，则模型（2）可转化为

本文采用轮廓最小二乘估计法估计模型（3）中的未知参数与未知函数[10]。具体步骤如下。

第一步：假设未知函数β(·)=（β1(·),…,βp(·))T已知，估计未知参数θ。

若β(·)=（β1(·),…,βp(·))T已知，则模型（3）可改写成线性模型

利用最小二乘法可得θ 的估计值为

第二步：估计未知函数β(·)=（β1(·),…,βp(·))T。

将模型（6）整理可得非参数模型

其中Q=W-WZT(ZWZT)-1ZW 为幂等矩阵。

为了估计模型（7）的未知函数β(·)=（β1(·),…,βp(·))T，最小化目标函数

非参数模型中未知函数的估计有多种方法[11]，本文采用B样条基函数近似方法来估计未知函数。

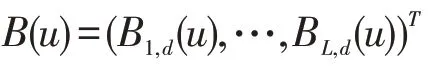
将式（9）代入式（8），令其对γ 的导数为0可得γ 的估计值为

其中，Sit=Ip⊗B(Uit)·Xit,i=1,2,..,n t=1,2,...,T

因此，未知函数β(·)的估计值为

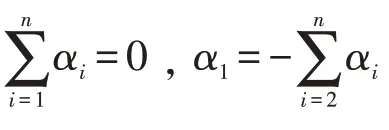
将Dα=D0α0代入模型（2）可得

其中

对于α0的估计，将模型（11）改写成线性模型

通过最小二乘法得出α0的估计值

3 模拟研究

上文利用B样条基函数来拟合未知函数，并采用轮廓最小二乘估计法估计固定效应部分线性变系数面板数据模型，本节利用Monte Carlo 模拟评估所得估计量的估计效果和模型拟合效果。为了评估参数θ 和未知函数β(·)的估计效果，对于参数θ 的估计量θ^ 计算均方误差（MSE），对于未知函数β(·)的估计量β^(·)计算均方根误差（RMSE）。为了评估模型的拟合效果，对于模型拟合效果的评估计算平均绝对误差（MAE）。本文中计算均方误差（MSE）、均方根误差（RMSE）和平均绝对误差（MAE）的方法如下：

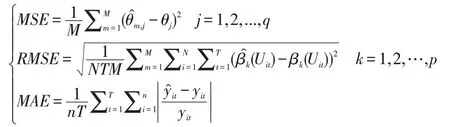
3.1 数据生成

模拟1 考虑如下模型：

（1）Xit,1，Xit,2，Xit,3，Xit,4均为来自于均匀分布U(-0.8,0.8)的样本。

（2）Uit为来自于均匀分布U(-0.8,0.8)的样本，函数β(u)的形式如下：

（3）Zit,1为来自于均匀分布U(-1,1)的样本，Zit,2为来自于均匀分布U(-2,2)的样本，

（4）参数θ1=2，θ2=3。

（5）固定效应αi为来自于正态分布N(0,1)的样本，随机误差项εit服从正态分布N(0,0.04)。

（6）{Zit} 、{ Xit} 均和{εit} 相互独立。

模拟2考虑如下模型：

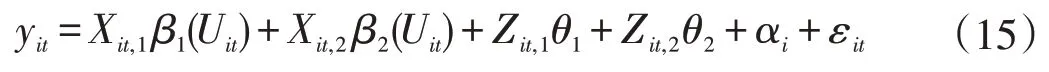
（1）Xit,1，Xit,2为来自于服从正态分布N(0,0.16)的样本。

（2）Uit为来自于均匀分布U(-0.8,0.8)的样本，函数β(u)的形式如下：

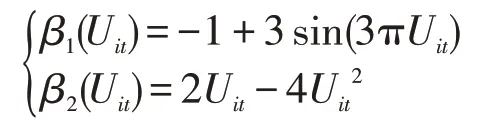
（3）Zit,1为来自于正态分布N(1,2.25)的样本，Zit,2为来自于正态分布N(0,1.69)的样本。

（4）参数θ1=2，θ2=3。

（5）固定效应αi为来自于正态分布N(0,1)的样本，随机误差项εit服从正态分布N(0,0.04)。

（6）{Zit} 、{ Xit} 均和{εit} 相互独立。

针对模拟1和模拟2，本文选取3次B样条基函数来拟合未知函数βk(Uit)，节点为均匀节点，取时间长度分别为T=4和T=6，样本量分别为n=50，n=100，n=150。

模拟1的数据生成及参数与未知函数估计过程如下：

（1）首先生成解释变量Xit=(Xit,1,Xit,2,Xit,3,Xit,4)和Z=(Zit,1,Zit,2)，Uit、固定效应αi与随机误差项εit的观测值，然后根据模型（14）计算出yit；

模拟2与模拟1的数据生成参数、未知函数和被解释变量拟合值的过程一致。

3.2 数据模拟结果

使用MATLAB软件对每一个数据的生成过程进行模拟，模拟次数为1000次，记录每一次的模拟结果，并计算评价指标MSE、RMSE和MAE。

根据表1可以看出，两个模拟下参数θ 的估计值和真实值，在样本量n和时间长度T不断变化的情况下均较为接近。说明了参数估计量在解释变量取自于不同分布的情况下均具有较好的估计准确性，表明了估计方法的优良性。

表1 参数θ 的模拟效果

首先，固定时间长度为T=4或T=6，随着样本量n的不断增加，均方误差（MSE）在逐渐减小。固定样本量n=50、n=100或n=150，随着时间长度T的增加，均方误差（MSE）在逐渐减小。当同时增加n和T时，均方误差（MSE）在逐渐减小。

根据表2可以看出，两个模拟下未知函数β(·)的估计值和真实值，在样本量n和时间长度T不断变化的情况下均较为接近。说明了未知函数估计量在解释变量取自不同分布的情况下均具有较好的估计准确性，表明了估计方法的优良性。

表2 未知函数β(·)的模拟效果

首先，固定时间长T=4或T=6，随着样本量n的不断增加，均方根误差（RMSE）在逐渐减小。固定样本量为n=50、n=100或n=150，随着时间长度T的增加，均方根误差（RMSE）在逐渐减小。当同时增加n和T时，均方根误差（RMSE）在逐渐减小。

图1 和图2 分别绘制了当样本量n=50，时间长度T=4 和样本量n=150，时间长度T=6 时，模拟1 中函数β1(Uit)、β2(Uit)、β3(Uit)和β4(Uit)的估计效果。

图3 和图4 分别绘制了当样本量n=50，时间长度T=4 和样本量n=150，时间长度T=6 时，模拟2 中函数β1(Uit)和β2(Uit)的估计效果。

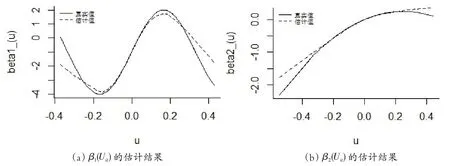
图3 n=50，T=4 模拟2中β1(Uit)、β2(Uit)的估计结果

同样，从图1至图4可以看出，模拟1和模拟2中未知函数的估计值和真实值在各种情况下均较为接近。同时，从图1和图2中可以观察到估计在峰值处存在“高峰低估，低峰高估”的趋势。

图1 n=50，T=4模拟1中β1(Uit)、β2(Uit)、β3(Uit)和β4(Uit)的估计结果

图2 n=150，T=6 模拟1中β1(Uit)、β2(Uit)、β3(Uit)和β4(Uit)的估计结果

图4 n=150，T=6 模拟2中β1(Uit)、β2(Uit)的估计结果

图5和图6分别绘制了当样本量n=50，时间长度T=4和样本量n=150，时间长度T=6时，yit在模拟1和模拟2中的估计结果。

根据图5和图6，可以看出在模拟1和模拟2中yit的估计值和真实值在各种情况下均较为接近，表明了模型的拟合效果良好。

图5 模拟1中yit的估计结果

图6 模拟2中yit的估计结果

根据表3可以看出，两个模拟下被解释变量的估计值和真实值，在样本量n和时间长度T不断变化的情况下均较为接近。说明了被解释变量在解释变量取自不同分布的情况下均具有较好的估计准确性，表明了模型的拟合效果良好。

表3 被解释变量的拟合效果

首先，固定时间长度T=4或T=6，随着样本量n的不断增加，平均绝对误差（MAE）在逐渐减小。固定样本量为n=50、n=100或n=150，随着时间长度T的增加，平均绝对误差（MAE）在逐渐减小。当同时增加n和T时，平均绝对误差（MAE）逐渐减小。

4 结论

本文研究面板数据模型，将参数模型的特点和非参数模型的特点融合在一起，相较于一般的模型，本文的模型引入了不可观测的个体固定效应，可以在很大程度上减轻内生性问题。

本文在采用轮廓最小二乘法估计模型的未知参数和未知函数的过程中，采用B样条基函数法近似未知函数。同时，还利用Monte Carlo模拟，结合模拟1和模拟2的结果，考察了当解释变量为取自于均匀分布和正态分布的样本时，估计量的估计效果和模型拟合效果，最终说明了估计方法在有限样本下具有良好的估计效果，模型的拟合效果良好。