桥式起重机主梁的平行六面体可靠性分析*

邢瑾文 高东鸣 张海牛 王 维

玉柴联合动力股份有限公司 芜湖 241080

0 引言

桥式起重机（以下简称桥机）主端梁连接技术对桥架有重要影响[1]。主梁是桥机的主要承载部件，约占整机金属结构自重的70%，对整机的安全性有重要作用，故研究桥机主梁结构的可靠性方法具有现实意义。在设计过程中，桥机主梁存在很多不确定性因素，当这些因素耦合在一起时，会在很大程度上对结构响应产生较大偏差，甚至面临失效风险。非概率可靠性模型正是在样本信息匮乏、难以准确定义概率性质的情形下于20世纪90年代提出，主张用凸集合描述不确定因素，以可靠性指标度量结构的安全程度，强调可接受行为的范围。因而，非概率可靠性模型适合于分析复杂的桥式起重机主梁结构。

Ben-Haim Y等[2，3]主张用凸集描述不确定参数，阐明了何为非概率可靠性，以结构所能容纳的不确定性的极限范围用于评判结构是否安全；郭书祥等[4]指出非概率可靠性指标是基于无穷范数刻画的标准空间中坐标原点到失效面的最短距离；王晓军等[5]将结构非概率可靠性指标重新定义为结构安全域和可行域的体积的比值，考虑以集合的思路度量结构安全性；姜潮等[6]于传统凸模型发展出一种变体——平行六面体模型，将独立和相关的不确定变量包含在一个统一的框架内，便于解决复杂不确定性的棘手难题；崔智勇等[7]将工程实际中的不确定性考虑为区间变量，研究了微粒群算法下区间模型非概率可靠性指标的计算；陈江义等[8]基于区间模型提出响应面模型的非概率可靠性优化方法；姜潮等[9]在已有的平行六面体模型基础上进行改进，在改进的平行六面体模型中，不确定参数间的相关系数被重新定义，基于相关矩阵进一步推导出不确定域的数学表达式，并应用到结构可靠性领域；为了克服现有凸模型公式的复杂性和多样性，姜潮等[10]又提出了构造非概率凸模型的统一框架，并提出凸模型建模方法的评价标准，作为后续新凸模型建模方法有效性验证的检验标准。

与区间模型和椭球模型相比，平行六面体模型可以很好地将变量间的独立性和相关性置于同一模型内分析，在保证结构可靠的同时成本得以有效控制。从某种意义上讲，平行六面体模型是更符合实际工程的一种凸模型，鉴于此，建立了桥式起重机主梁的平行六面体非概率可靠性模型。实例表明，平行六面体模型的运用能较准确地描述起重机结构的可靠性。

1 基于凸模型的非概率可靠性

1.1 基于区间模型的非概率可靠性

假设所有不确定参数之间相互独立，且在已知区间或超长方体内变化，即

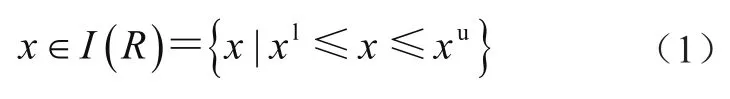
式中：xl、xu分别为区间变量x的下界、上界。

定义区间变量x的均值和离差分别为

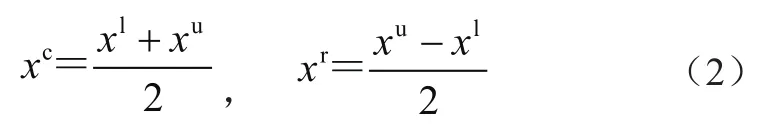
将区间变量投影到标准化区间变量的度量上，这一过程称为标准化，具体转换过程为

然后，将标准化后的变量带入功能函数，即

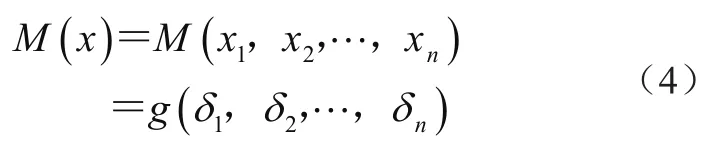
在此失效模式下的区间模型非概率可靠性指标采用无穷范数表示，即

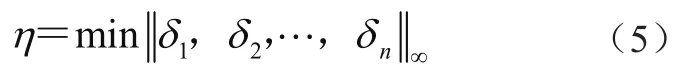
其几何意义为：在标准化区间变量张成的扩展空间里，以无穷范数度量的n维空间中坐标分量到失效面的最短距离，扩展空间是指其扩展后的无限空间。若极限状态函数简单，有学者主张采用定义法、转换法和优化法进行可靠性指标的求解。同时，结构的极限状态面将整个标准化空间划分成2个域：失效域和安全域。当η＝1时，失效面与凸域刚好相切，结构性能处于临界失效状态；当η＝＞1时，结构性能的实际波动范围均处于安全区内，与失效面没有交集，结构可靠，且η的值越大，结构也越可靠。

1.2 基于椭球模型的非概率可靠性

假设不确定参数之间具有相关性，且在已知椭球体内变化，即

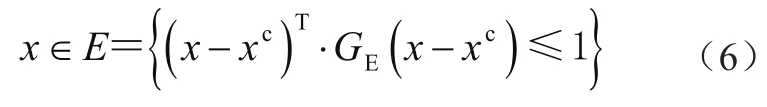
在实际情况下，常常将不确定参数向量x无量纲化为相对变差向量δ，两者的分量元素关系式为

式中：为名义值。

椭球模型用超椭球集合界定变差向量δ，其表达式为

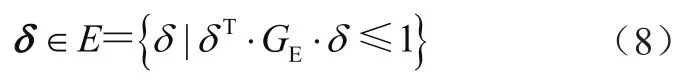
引入标准化向量

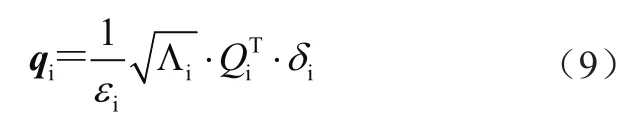
式中：Qi、Λi分别为超椭球形状矩阵Wi的特征向量和特征值对角矩阵，有

经过变换，原凸模型转换为标准化q空间下，即

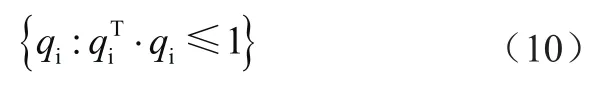
用Euclidean范数定义标准q空间中向量的长度为

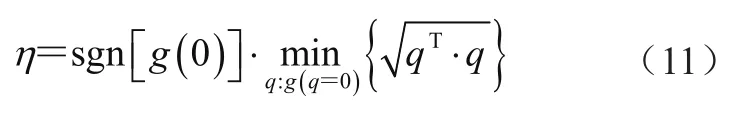
其几何意义为：标准化空间的坐标原点到极限状态曲面的最短距离。经过标准化处理后，单位值1可作为结构性能是否可靠的标尺。当η＝1时，极限状态曲线与凸域相切，恰好位于临界失效处；当η＞1时，不确定参数的变差均在安全域内，结构性能保留有一定程度的安全余量。

1.3 基于平行六面体模型的非概率可靠性

假设不确定参数之间具有相关性，且在一直平行六面体内变化，即

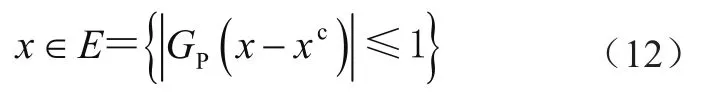
如图1所示，将不确定参数进行标准化，转换过程可表示为

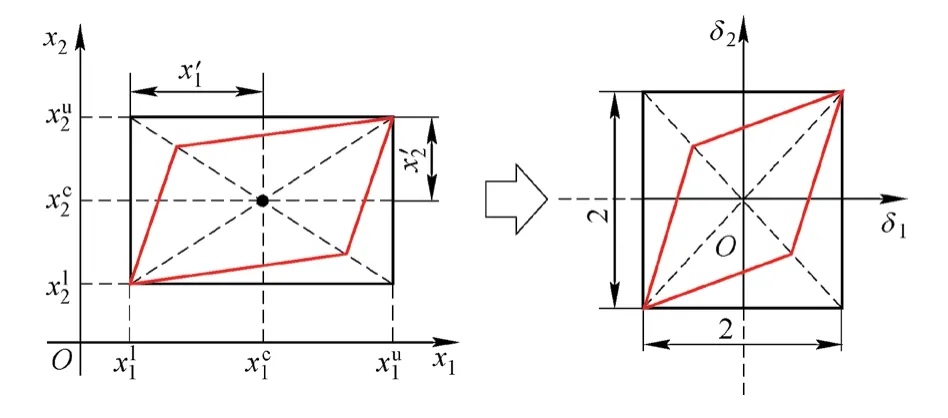
图1 平行六面体模型的二维区间变量的标准化过程

任意2个变量间的相关系数可定义为

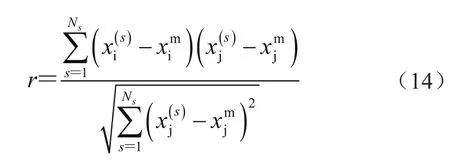
进一步相关矩阵可描述为

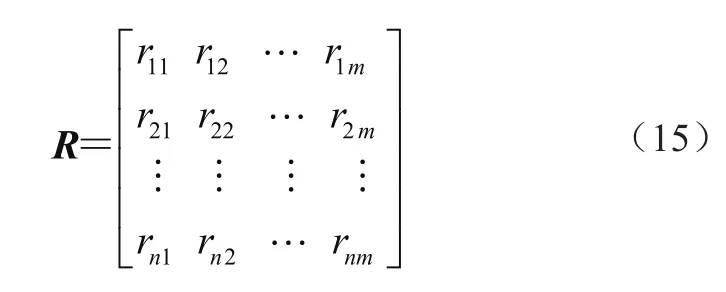
特征矩阵定义为

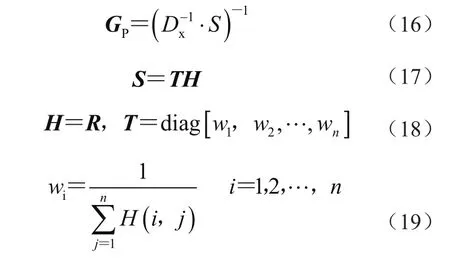
由此得到包络所有区间变量的平行六面体域为

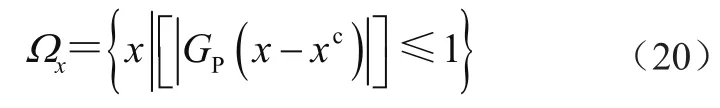
可以借助不确定域中的点到失效平面G（δ）＝0之间的最短距离来评判系统是否安全可靠，故构建一个优化问题来得到系统的非概率可靠性指标η

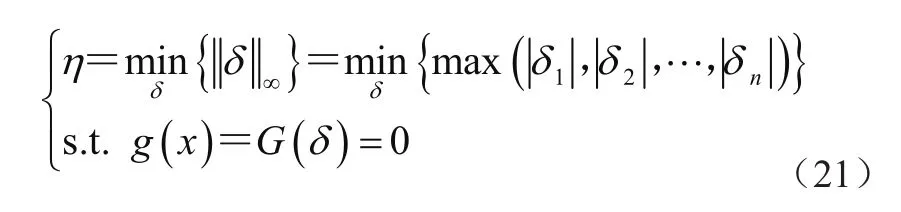
前述最短距离是基于无穷范数来进行衡量的，而最优点则是指失效平面上的设计验算点。在几何空间中，最优点是当不确定域均匀地向外扩展时和失效平相切时的第一个点。图2描述了二维空间中基于多维平行六面体模型的可靠性指标定义。

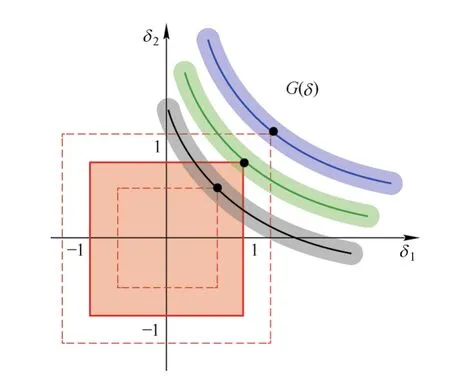
图2 平行六面体模型的非概率可靠性度量指标示意图

2 数值算例和工程应用

2.1 悬臂梁

研究图3所示悬臂梁的不确定性参数的量化，并进行非概率可靠性分析，悬臂梁的梁中弯矩最大值应小于极限弯矩。极限状态函数可表示为

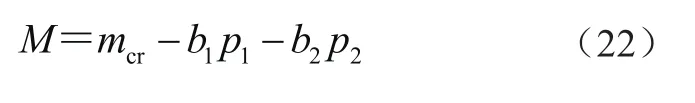
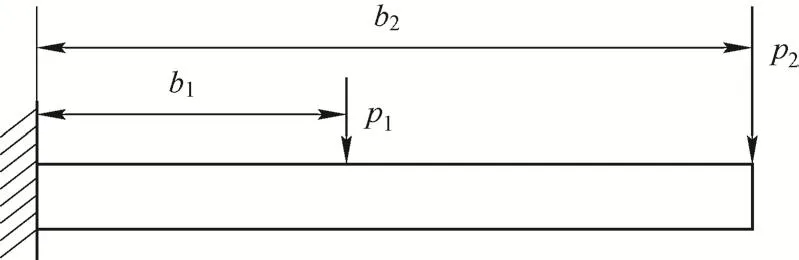
图3 悬臂梁

在距固定端为b1＝2.0 m，b2＝5.0 m，处分别作用2个集中载荷p1和p2。设基本区间变量为的取值范围给定7种情况，分别基于区间、平行六面体和椭球3种模型计算结构的可靠性指标，结果如表1所示。

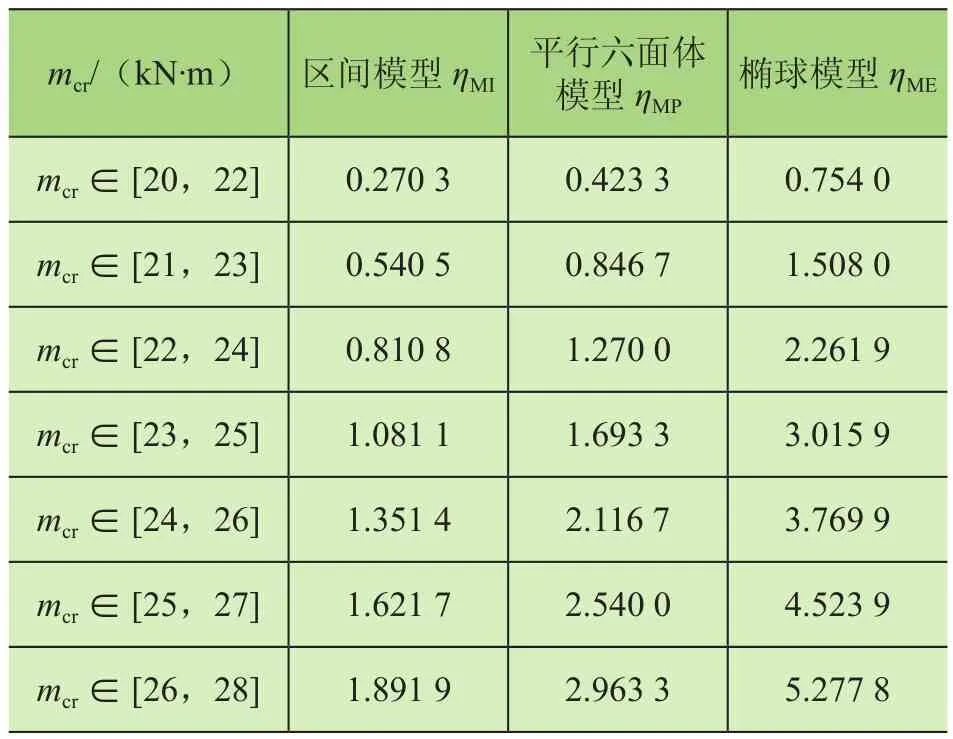
表1 基于不同凸模型的非概率可靠性指标的比较

比较3种方法的结果，可得到如下结论：

1）随着极限弯矩mcr不确定范围的逐渐增大，可靠性指标呈逐渐上升的趋势，η越大，结构越可靠。

2）无论极限弯矩mcr的区间范围变化多大，基于区间模型计算的可靠性指标始终较保守，即若区间模型算出的可靠性指标η＞1，则椭球模型和平行六面体模型算出的可靠性指标必定使结构可靠。另外，在实际工程中，区间模型非概率可靠性往往容易造成材料不必要的浪费，加大制造成本。

3）由于椭球模型考虑了变量间的相关程度，故相对区间模型而言是更合理的。由表1的结果对比可知，同区间模型和平行六面体模型相比，椭球模型计算出来的非概率可靠性指标总是最大的，这主要是由于椭球模型无法考虑任意2个变量间独立的情形造成的。与区间模型不同，椭球模型非概率可靠性往往容易出现过危险设计。

4）平行六面体模型计算出的非概率可靠性指标介于区间模型和椭球模型两者之间，既不像区间模型那样过保守，也不像椭球模型那般过危险，可以很好地将变量间的独立性和相关性置于同一模型内分析，在保证结构可靠的同时成本也有效地得到控制。因此，在某种程度上，平行六面体模型是更符合实际工程的一种凸模型。

2.2 桥机主梁结构

1）基本参数及结构校核

以某起重量为32 t的桥机偏轨箱形梁为例进行可靠性分析，该桥机的基本参数如表2所示。考虑到实际工程中不确定性因素的客观存在，且难以获得大量的试验数据信息，将额定起重量、吊具质量、小车质量、许用强度及弹性模量等5个不确定性参数看成区间变量，并分别以x1、x2、x3、x4、x5表示，区间范围分别为：x1＝[28.8，35.2]，x2＝[0.9，1.1]，x3＝[9.9，12.1]，x4＝[158.4，193.6]，x5＝[1.8×105，2.2×105]。根据给定的区间范围可求出相应的均值和离差，具体参数如表3所示。

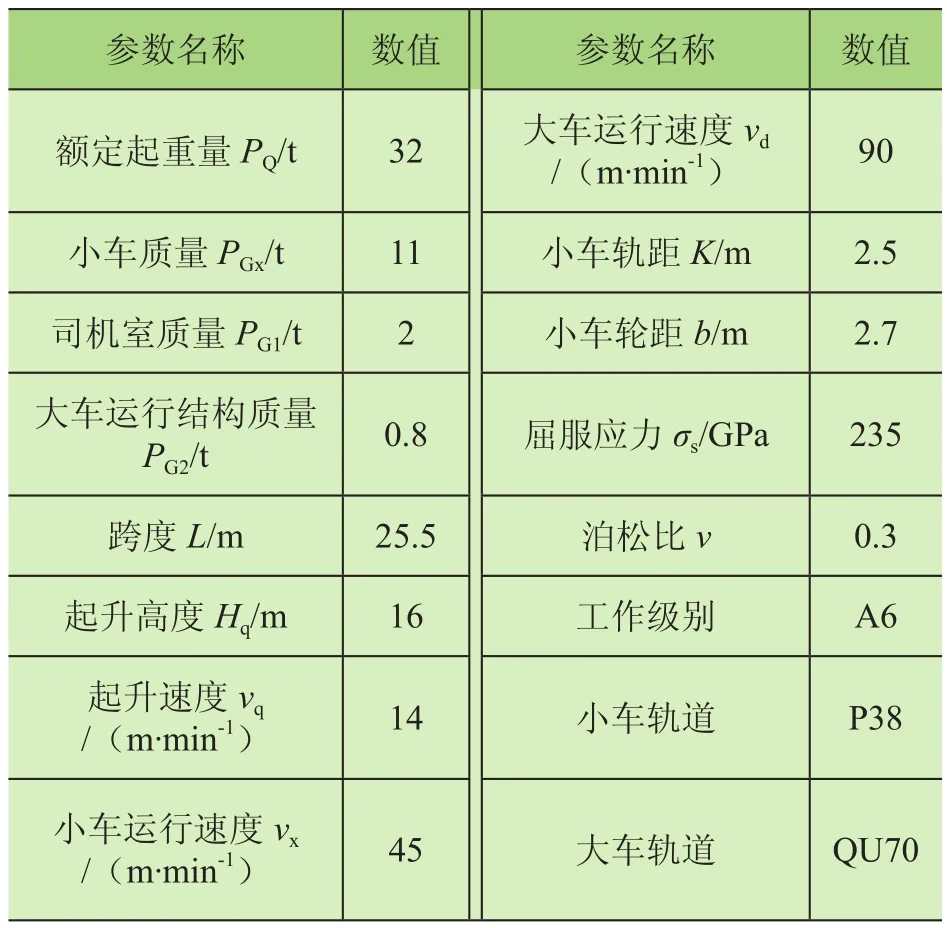
表2 桥机基本参数表

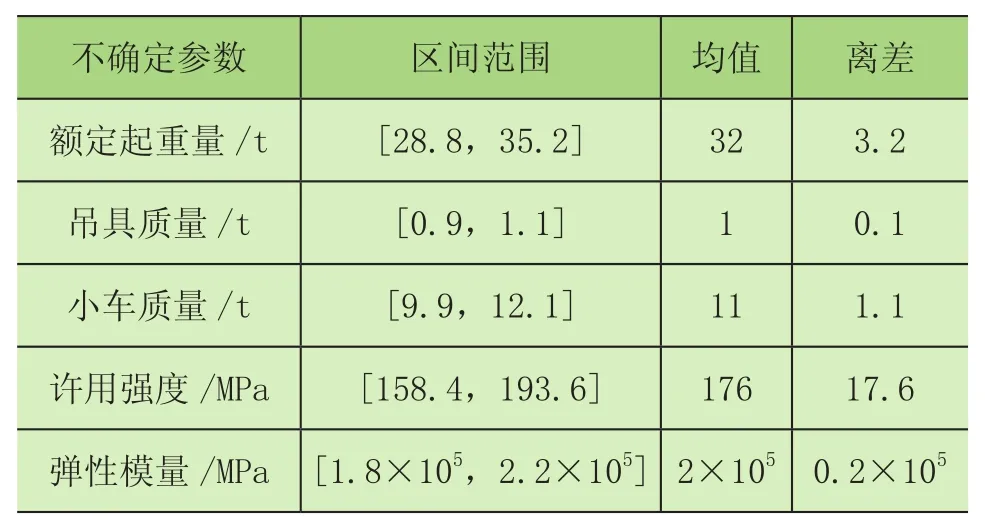
表3 不确定参数的区间范围及其均值、离差

对于桥机主梁，其稳定性往往满足要求，而强度和刚度通常为结构的主要破坏形式，为此只考虑桥机主梁结构的强度和刚度可靠性问题，需要校核偏轨箱形梁跨中截面3个验算点的强度，如图4所示。

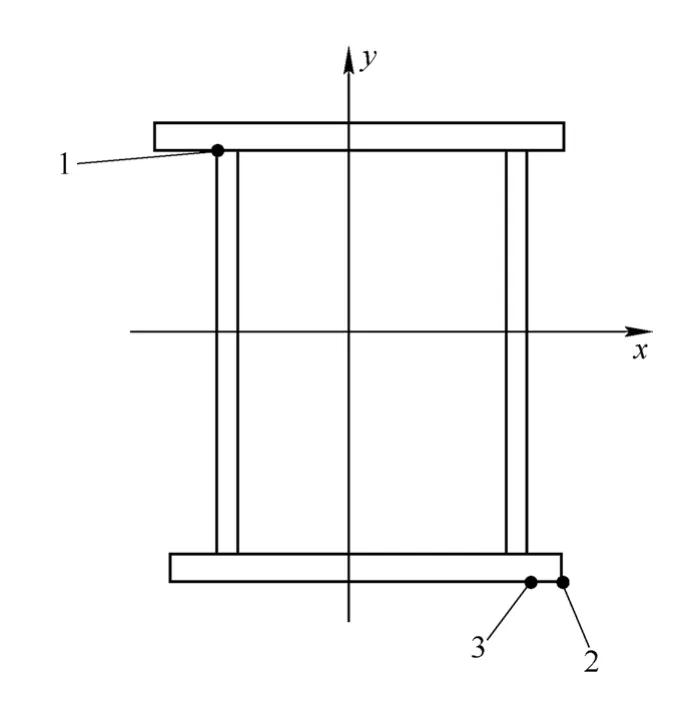
图4 主梁截面强度验算示意图

其中，主腹板边缘点1处的极限状态函数为

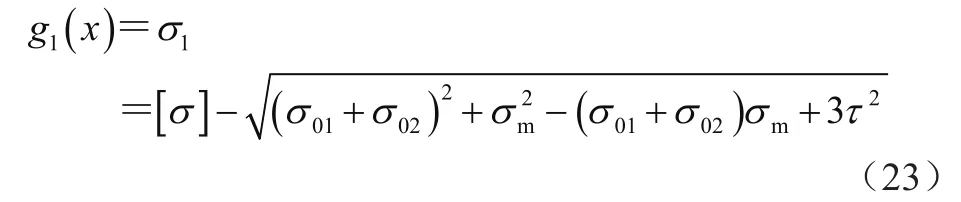
式中：[σ]为许用强度，σ01为垂直弯矩产生的应力，σ02为水平弯矩产生的应力，σm为主腹板边的局部压应力，τ为主腹板边的切应力。

下盖板点2处的极限状态函数为

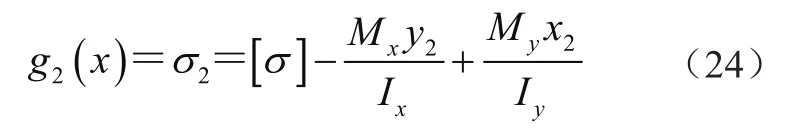
式中：[σ]为许用强度，Mx为主梁跨中总的弯矩，My为主梁跨中总的水平弯矩，x2、y2为形心位置，Ix、Iy为惯性矩。

下盖板点3处的极限状态函数为

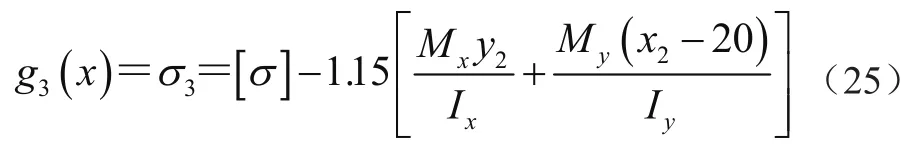
式中：[σ]为许用强度，Mx为主梁跨中总的弯矩，My为主梁跨中总的水平弯矩，x2、y2为形心位置，Ix、Iy为惯性矩。

此外，还应校核结构的静刚度，其极限状态函数为

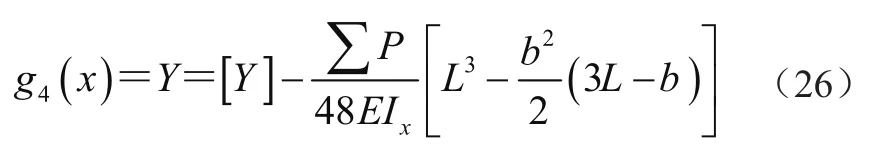
式中：[Y]为许用静挠度，这里为满载小车总静轮压，E为弹性模量，L为跨度，b为小车轮距。

2）平行六面体模型可靠性分析

在构建强度的平行六面体模型时，根据极限状态函数，共涉及额定起重量、吊具质量、小车质量、许用强度4个不确定性参数。将不确定性参数x1、x2、x3、x4标准化，转化关系如式(13)，基于平行六面体模型对桥机主梁结构的强度进行非概率可靠性分析时，由式(14)和式(15)可得该模型的相关矩阵为

按照式(16)计算该模型的特征矩阵为

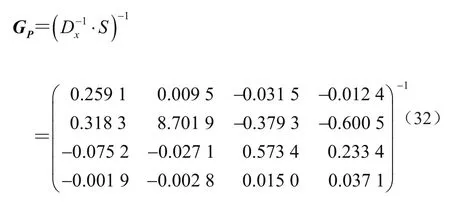
基于强度的平行六面体模型的不确定域为

所以，采用无穷范数进行该模型的非概率可靠性分析，则有

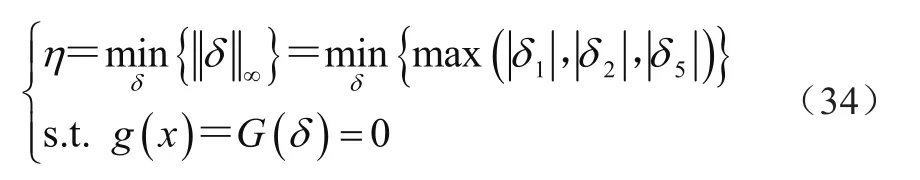
在构造刚度的平行六面体模型时，首先对不确定性参数额定起重量、吊具质量、小车质量、弹性模量等进行标准化，转化关系如式(13)，由式(20)可以得到式（35）所示基于平行六面体模型的结构刚度的不确定域，即

基于平行六面体模型对桥机主梁结构刚度的非概率可靠性分析过程与上述相同，计算结果见表4。

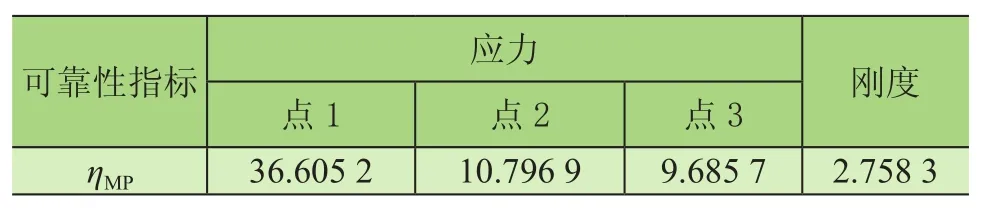
表4 主梁结构强度和刚度非概率可靠性指标计算结果

通过分析计算结果，基于平行六面体模型对桥机主梁结构的可靠性分析，有关结构强度和刚度的非概率可靠性指标都大于1，表明桥机主梁结构是安全可靠的。桥机主梁结构的整体非概率可靠性应由最危险的情形确定，针对所研究的目标起重机主梁可靠性指标为2.758 3＞1，且有一定的安全余量，能满足使用要求。

3 结论

1）从不确定域的量化、可靠性指标的计算、适用范围等方面分别探讨了区间模型、椭球模型和平行六面体模型的非概率可靠性，通过悬臂梁数值算例，表明基于平行六面体的非概率可靠性模型相对比较合理，较好地解决了其他模型过保守或过危险的设计问题。

2）提出了基于平行六面体的桥机主梁结构的非概率可靠性分析方法，该方法可在确保经济的基础上很好地分析结构可靠性问题，具有一定工程价值。

此外，本文方法还可拓展至概率—模糊—平行六面体模型混合可靠性问题中，进一步拓展平行六面体模型在实际工程结构设计中的应用能力。