LOCA工况下环形燃料元件内包壳外压屈曲试验研究

武 琦，刁均辉，季松涛，何晓军，关玺彤，李 凯，高永光

(中国原子能科学研究院 反应堆工程技术研究所，北京 102413)

环形燃料是一种新型结构的压水堆核燃料，环形燃料元件由内、外两层锆合金包壳和圆环状的UO2芯块组成，冷却剂可同时从内、外两个流道对燃料元件进行冷却，具有功率密度高、运行温度低和安全裕量大等优点[1-5]。压水堆冷却剂丧失事故(LOCA)是指反应堆主冷却剂系统冷管段或热管段出现大孔直至双端剪切断裂并同时失去厂外电源的事故，是压水堆的极限设计基准事故[6-7]。压水堆LOCA过程中，燃料元件快速升温，内部气腔压力增大而外部冷却剂压力丧失，因此不可避免地会出现包壳鼓胀爆破[8]、受热受压变形而失效的现象。相比于传统棒状实心燃料，环形燃料元件有内、外两层包壳，在LOCA工况下外包壳受内压鼓胀而内包壳受外压屈曲，失效的形式比较复杂，且不同的失效形式可能会导致不同的后续分析结果和响应动作。

为对环形燃料元件LOCA下整体受压失效形式的问题进行研究，有必要在堆外开展针对环形燃料元件内包壳在LOCA下失效行为的试验研究。

1 试验目的

当压水堆发生LOCA时，燃料元件快速升温，对燃料元件的包壳主要带来了两方面影响：首先，燃料元件包壳材料(主要是锆合金)的强度随温度升高而下降，同时形成氧化锆使得塑性降低；其次，燃料元件包壳所受压力随温度升高而增大。LOCA过程中燃料元件包壳的受压失效主要是由于温度升高带来的材料性能降低和压力增大两种效应共同导致的。

对于环形燃料元件内包壳而言，LOCA下的失效形式主要是受外压而发生屈曲。对环形燃料元件内包壳的失效形式试验研究，主要是在堆外模拟LOCA工况下，燃料元件升温过程中环形燃料元件内包壳发生外压屈曲的行为，获得环形燃料元件内包壳发生外压屈曲时的压力与温度的关系，为环形燃料的分析和计算提供支撑。同时获得其外压屈曲后的形态，便于理解环形燃料元件内包壳外压屈曲的过程并分析其影响因素。环形燃料元件结构如图1所示。

图1 环形燃料元件示意图Fig.1 Schematic diagram of annular fuel element

2 试验装置

堆外环形燃料元件内包壳LOCA下外压屈曲试验的装置主要为3个部分：试验件、环形燃料模拟芯块和电加热棒。试验件为一段890 mm长的环形燃料元件内包壳，径厚比为16.4，材料是未受过辐照和氧化的新鲜Zr-4合金。环形燃料模拟芯块模拟了实际环形燃料芯块的大小，可减小气腔，使试验工况更接近于实际情况。为了增加热传导，采用铜制造。电加热棒为特别设计和制造的环形电加热棒(内部中空)，额定电压为220 V，额定功率为3.6 kW，发热段长度为600 mm。

试验件、环形燃料模拟芯块和电加热棒通过焊接连接并密封，在外部裹上保温层以减少散热。通过引压管，用氩气气瓶将内部密封气腔充压至试验压力，将热电偶安装在试验件的内表面进行测温。试验中试验件的升温速率约为3～5 ℃/s。试验装置设计图如图2所示。

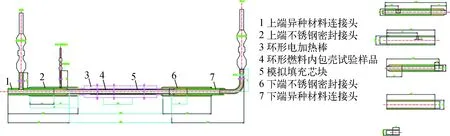
图2 试验装置设计图Fig.2 Design drawing of experiment device

3 试验结果

3.1 单棒试验结果

某一典型试验工况下，试验过程中温度和压力的状态及变化如图3所示。根据理想气体状态方程，在固定容积的气腔内随着气体温度的上升，气腔压力应该增大。因此当试验过程中气腔压力不但没有缓慢上升反而发生突降时，认为试验件发生了外压屈曲，导致试验装置的气腔容积变大从而压力下降，试验件屈曲时会发出“啪”的一声轻微脆响。温度1和温度2分别由布置在试验件轴向中心(445 mm长度处)、周向间隔180°的两根热电偶测量而得，取开始发生屈曲时温度1和温度2中较高的温度作为对应的屈曲温度。

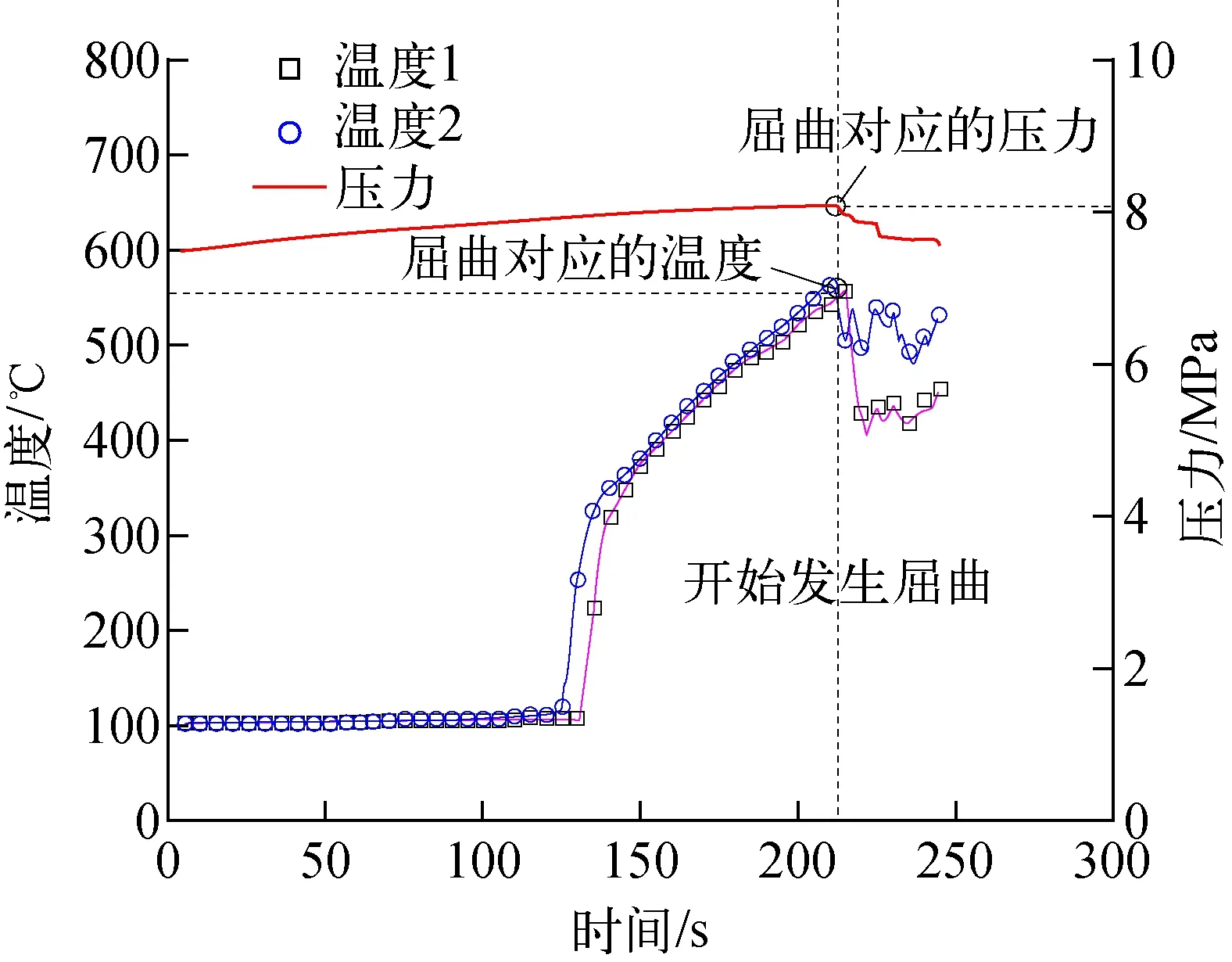
图3 试验过程中参数的变化Fig.3 Parameter change during experiment

每次试验后采用专用的切割解体装置，在不破坏试验件形貌的前提下，将试验装置进行拆解，得到试验后的试验件，其外观如图4所示。从试验件的外观形貌可看出，试验件在轴向形成屈曲半波，大部分试验件形成1个轴向屈曲半波，少数形成两个轴向屈曲半波。

图4 试验后的试验件Fig.4 Experiment sample after experiment

3.2 整体试验结果

在不同的初始内压下，对试验装置进行加热，逐一完成上述单棒试验，所有试验后的试验件如图5所示。对所有试验件进行测量，发现试验屈曲后的变形段长度分布在220～350 mm之间。按照图3取每个单棒试验开始发生屈曲时的压力和温度，所有试验件屈曲时压力和温度的关系如图6所示。

图5 所有试验后的试验件Fig.5 All experiment samples after experiment

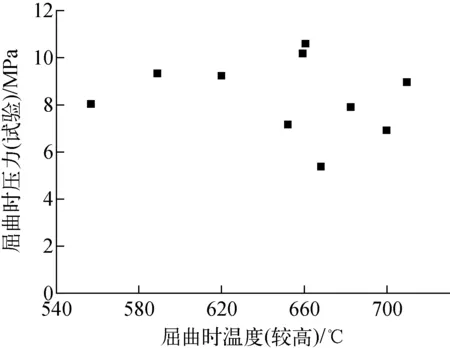
图6 屈曲时压力和温度的关系Fig.6 Relationship between pressure and temperature at beginning of buckling

4 试验结果分析

4.1 试验结果校核

在压力容器设计标准中有外压容器许用外压设计的内容，如果根据设计标准或公式得到了外压容器在某一工况下的许用外压，由于设计的保守性，可以推测设计许用外压应低于试验屈曲压力。

常用的外压设计标准如GB 150—2011中第3章第4节[9]和ASME第Ⅷ-1卷[10]中的图算法，都没有给出锆合金材料的外压设计曲线，对于本试验中Zr-4材料制造的试验件难以适用。由于试验工况的温度较高，ASME第Ⅷ-2卷中推导外压曲线的MPC模型也难以适用[11]。在GB 150—2011中采用了Bresse-Bryan公式来计算容器外压屈曲时的临界压力，并选取安全系数m，计算得到的临界压力除以m便为设计许用外压[p][12]。参照GB 150—2011中的方法，对试验时屈曲温度下的锆合金许用外压进行计算，作为试验结果的对比参考。Bresse-Bryan公式[12-13]的具体形式为：

式中：pcr为计算临界压力，MPa；E为弹性模量，MPa；μ为泊松比；δe为有效壁厚，mm；D0为外径，mm。温度T下的Zr-4合金的弹性模量E按下式[14]计算：

E=1.088×105-54.7TT≤1 090 K

E=4.912×104-48.27T

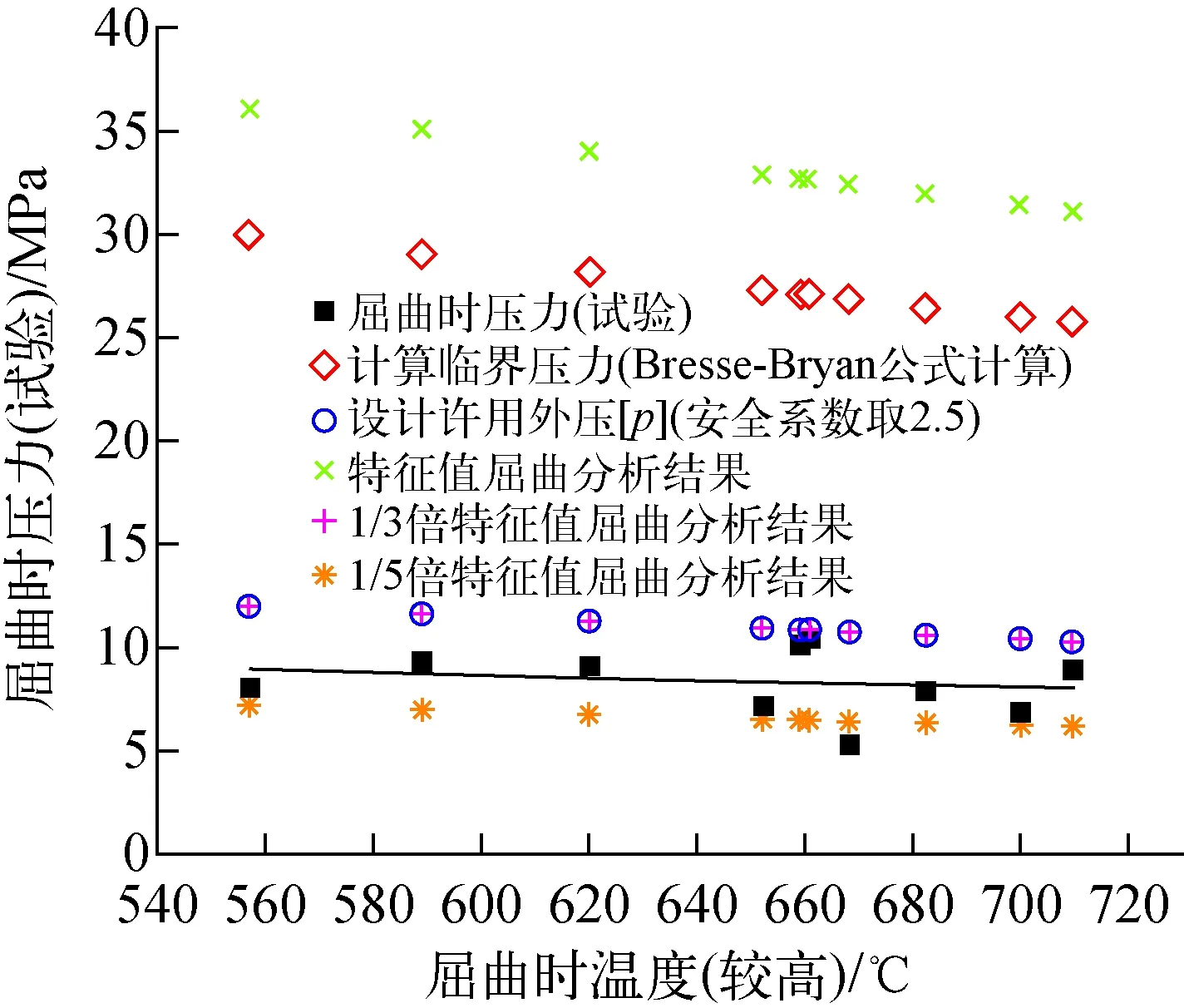
1 090

E=max(1.0×104，9.21×104-40.5T)

T>1 240 K

温度T下的Zr-4合金的泊松比μ按下式[14]计算：

μ=0.338 5-1.689×10-4T

根据文献[12]，m按以下方式取值：

将环形燃料元件内包壳试验件的径厚比D0/δe=16.4代入，得到m=2.5。

临界压力pcr、设计许用外压[p]和试验屈曲压力与发生屈曲时温度的关系如图7所示。由图7可看出，参照GB 150—2011中计算容器外压的方法，结合MATPRO中的锆合金物性参数[14]，在各种试验工况下推导出的设计许用外压[p]均高于试验屈曲压力，用于环形燃料元件内包壳的计算和分析是不保守的。

图7 屈曲时压力和温度的比较Fig.7 Comparison of pressure and temperature at beginning of buckling

4.2 数值模拟分析

对试验件和试验条件进行一定程度的简化，在ANSYS中进行特征值屈曲数值模拟分析。首先对试验件进行了建模，长600 mm，边界条件设置为两端固支，受外表面法向压力。材料物性参数用4.1节中的公式计算后输入。建模、网格划分及网格质量如图8所示[15]。特征值屈曲模拟分析计算后的结果如图9所示。

图8 试验件模型网格及质量Fig.8 Mesh and quality of experiment sample model

图9 试验件特征值屈曲数值分析结果Fig.9 Numerical analysis result of eigenvalue buckling of experiment sample

对所有试验工况进行模拟分析，屈曲时的压力和温度关系如图10所示。

图10 试验、计算和模拟分析结果Fig.10 Experiment,calculation and simulation analysis results

由图10可见，在所有试验工况下，特征值屈曲模拟分析得到的结果乘以1/3与参照GB 150—2011中方法计算得到的设计许用外压[p]几乎吻合，但均略高于试验值，特征值屈曲模拟分析得到的结果乘以1/5基本都低于试验值。

4.3 试验结果的公式拟合

试验结果的公式拟合如图11所示。由图11可见，采用Bresse-Bryan公式计算和特征值屈曲模拟分析的结果中，屈曲时的压力和温度均呈线性关系，其斜率介于1/5～1/3倍特征值屈曲模拟的压力与温度关系之间。因此对试验中屈曲时的压力和温度进行线性拟合，拟合公式为：

图11 试验结果的公式拟合Fig.11 Formula fitting of experiment result

p=-0.006 09T+12.342 15

式中，p为试验屈曲时压力，MPa。

根据试验结果，拟合公式适用于升温速率为3～5 ℃/s，在550～720 ℃之间发生外压屈曲的新鲜环形燃料元件内包壳。

5 结论

本文对890 mm长、径厚比为16.4的Zr-4合金的环形燃料元件内包壳试验件，在两端固支、不同外压作用时，中间600 mm段以3～5 ℃/s的升温速率进行升温，研究外压屈曲时的压力和温度关系，得到如下结论。

1)试验结果的整体趋势合理，对试验结果进行了公式拟合，可初步用于环形燃料元件内包壳的分析和计算。

2)参照GB 150—2011中计算容器外压容器的方法，结合MATPRO中的锆合金物性参数和环形燃料元件内包壳试验件的尺寸参数，在各种试验工况下推导出的设计许用外压[p]均高于试验屈曲压力，用于环形燃料元件内包壳的计算和分析是不保守的；采用特征值屈曲数值模拟分析，发现试验结果分布于特征值屈曲数值模拟分析结果的1/5～1/3之间。

3)环形燃料元件内包壳发生外压屈曲时的压力除了受温度的影响，还可能受到升温速率、氧化程度、周向温差、椭圆度、残余应力和屈曲形态等因素的影响。后续可采用控制变量法开展针对上述单一变量的试验研究，逐步完善试验屈曲压力p的经验计算公式。