改进的G-布朗运动驱动的随机微分方程的稳定性
高亚楠,吕 文
(烟台大学数学与信息科学学院,山东 烟台 264005)
随机稳定性一直是随机微分方程理论和应用研究中的核心议题[1-2]。自从PENG[3]建立了G-期望、G-布朗运动理论和相应的随机计算以来,学者们对G-布朗运动驱动的随机微分方程(简称G-SDEs)解的存在性、唯一性和稳定性进行了大量的研究[4-11],其中文献[6]研究了由G- 布朗运动驱动的随机微分方程的可解性和稳定性;文献[10]考虑一类由G-布朗运动驱动的脉冲随机微分方程,利用Lyapunov函数方法,建立了此类微分方程平凡解的p阶矩稳定性和p阶矩渐近稳定性的若干判据;文献[11]证明了一类由G-布朗运动驱动的多值随机微分方程解的存在唯一性。就我们所知,多数关于G-SDE的解的稳定性结果都是基于G-Lyapunov函数的无穷小算子为负定的约束条件得到的。为了研究线性时变系统和时变时滞系统的稳定性,文献[12] 和[13] 引入了一致渐近稳定函数(UASF),文献[14]基于这种一致渐近稳定函数构造了一些新的稳定性定理,取消了对引入的不定函数的一些约束。关于随机非线性系统,文献[15]利用一致渐近稳定函数,提出了一系列新的稳定性(不稳定性)判据。
在上述工作的启发下,本文旨在减弱对G-Lyapunov函数的约束,利用UASF对由G-布朗运动驱动的随机微分方程给出新的稳定性(不稳定性)判据。本文第1部分将介绍一些基本概念;第2部分中,讨论了关于G-SDE的新型稳定性定理;第3部分研究了G-SDE的失稳判据;最后对本文结果进行了总结。
1 预备知识和基本假设
下面介绍有关G-期望、G-布朗运动及相关随机微积分的一些基本概念。
令Ω为取值n上的初值为0的连续函数ωt的全体,定义其中任意两过程之间的距离为
ρ(ω1,ω2)=
对于t∈[0,∞),
·Bt(ω):=ωt,ω∈Ω。
·B(Ω):Ω的Borelσ-代数,Ωt={ω·Λt:ω∈Ω}, Ft:=B(Ωt)。
·Lip(Ω):={φ(Bt1, …,Btn):n≥1,t1, …,tn∈[0,∞),φ∈Cb,Lip(d ×n)},其中Cb, Lip(d ×n)为d ×n上有界的Lipschitz函数全体。
·L0(Ω)为B(Ω)-可测实值函数全体,L0(Ωt)为B(Ωt)-可测实值函数全体。
·B(Ω)中连续元素全体记为Cb(Ω) ,Cb(Ωt):=Cb(Ω)∩L0(Ωt)。
·Lip(Ωt):=Lip(Ω)∩L0(Ωt)。
定义1 记u(t,x)是下列PDE的粘性解:

[φ(B(t)+x)]:=u(t,x),
则B(t)是G-期望空间(Ω,Lip(Ω),(·))中的G-布朗运动,而且B(t)服从G-正态分布
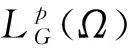
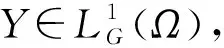
其中EP是关于P的线性期望。对于P,相关的容度定义为
C(A):=supP∈PP(A),A∈B(Ω)。
定义2 如果C(A)=0,则称集合A∈B(Ω)为极集。如果一个性质在一个极集之外成立,那么它就被称为拟必然成立(简称q.s.)。


j=1,2, …,N-1。
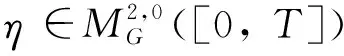
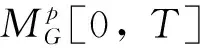

记〈B〉(t)是B(t)的二阶变差过程,即
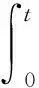

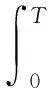
引理1 对于M0∈,和过程
是一个G-鞅。

(ηtdB(t))=0,
本文考虑如下形式的由G-布朗运动驱动的n维随机微分方程(G-SDE)。
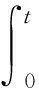
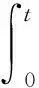
(1)
其中x0∈n是初值,B(·)是一维G-布朗运动。〈B〉(·)是G-布朗运动B(·)的平方变差过程。系数且f(t,0)=h(t,0)=g(t,0)≡0。由于本文主要研究稳定性结果,因此假设对任意初值x0,方程的解总是存在的,记为x(t)。
定义G-Lyapunov算子为
LV(t,x)=Vt(t,x)+Vx(t,x)f(t,x)+
G(〈Vx(t,x),2h(t,x)〉+
〈Vxx(t,x)g(t,x),g(t,x)〉)。
定义5 记初值为x(0)=x0,x0∈n的G-SDE的解为x(t),其平凡解称为
(1)指数p-稳定,如果存在常数C,λ>0,有
[|x(t)|p]≤C|x0|pe-λt;
(2)指数p-不稳定,如果存在常数C,λ>0,有
[|x(t)|p]≥C|x0|peλt。
为了研究线性时变系统的稳定性,推广时变时滞系统的Razumikhin和Krasovskii稳定性定理,文献[12]和[13]引入了一致渐近稳定函数。


2 稳定性定理
本节将讨论G-SDE (1)的新的稳定性条件。
定理1 对于方程(1),如果存在V(t,x(t))∈C1,2([0,∞)×n;+),常数α1,α2,p>0和UASFμ(t)使得对所有的t∈[0,∞):
(2)
则G-SDE (1)的平凡解是指数p-稳定的。

(Vt(t,x(t))+Vx(t,x(t))f(t,x(t)))dt+
Vx(t,x(t))h(t,x(t))d〈B〉t+
Vx(t,x(t))g(t,x(t))dB(t)]=
(Vt(t,x(t))+Vx(t,x(t))f(t,x(t)))dt+
Vx(t,x(t))h(t,x(t))d〈B〉t+
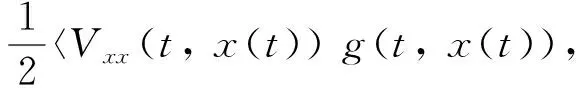
g(t,x(t))〉d〈B〉t+
Vx(t,x(t))g(t,x(t))dB(t)]+
〈Vxx(t,x(t))g(t,x(t)),g(t,x(t))〉))dt-
〈Vxx(t,x(t))g(t,x(t)),g(t,x(t))〉))dt=
Vx(t,x(t))g(t,x(t))dB(t)]+dMt,
其中
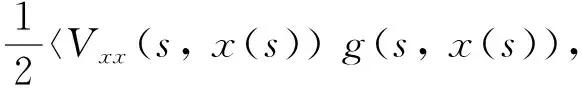
g(s,x(s))〉]d〈B〉s-
〈Vxx(s,x(s))g(s,x(s)),g(s,x(s))〉))ds。
由上式可得
Vx(s,x(s))g(s,x(s))dB(s)]+Mt。
V(0,x0)≤
由式(2),
V(0,x0)≤0,
故

由式(2),可得
α1|x(t)|p≤α2|x0|peσe-λt,
因此
即G-SDE (1)的平凡解是指数p-稳定的。
3 不稳定性定理
定理2 对于G-SDE (1),如果存在V(t,x(t))∈C1,2([0,∞)×n;+),常数α1,α2,p>0和UASFμ(t)使得对所有的t∈[0,∞):
(3)
则G-SDE (1)的平凡解是指数p-不稳定的。

(Vt(t,x(t))+Vx(t,x(t))f(t,x(t)))dt+
Vx(t,x(t))h(t,x(t))d〈B〉t+
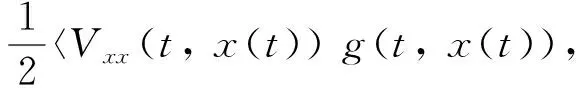
g(t,x(t))〉d〈B〉t+
Vx(t,x(t))g(t,x(t))dB(t)]=
(Vt(t,x(t))+Vx(t,x(t))f(t,x(t)))dt+
Vx(t,x(t))g(t,x(t))dB(t)+
Vx(t,x(t))h(t,x(t))d〈B〉t+
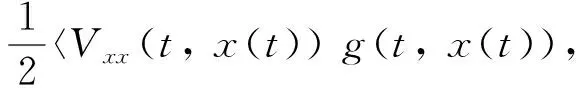
g(t,x(t))〉d〈B〉t]+
〈Vxx(t,x(t))g(t,x(t)),g(t,x(t))〉))dt-
〈Vxx(t,x(t))g(t,x(t)),g(t,x(t))〉))dt=
Vx(t,x(t))g(t,x(t))dB(t)]+dMt,
其中
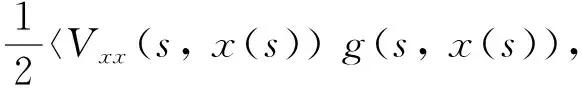
g(s,x(s))〉]d〈B〉s-
〈Vxx(s,x(s))g(s,x(s)),g(s,x(s))〉))ds。
由上式可得
Vx(s,x(s))g(s,x(s))dB(s)]+Mt。
两边取G-期望可得
V(0,x0)≤
LV(s,x(s))ds]≤0,
故
eλt-σV(0,x0)。
由式(3)可得
即G-SDE (1)的平凡解是指数p-不稳定的。
4 总 结
对于由G-布朗运动驱动的随机微分方程,本文给出了新的稳定性和不稳定性定理。特别地,当μ(t)=-λ时即得文献[6]中的结果,故本文的结果减弱了对G-Lyapunov函数的约束。

