图运算下的电阻距离与基尔霍夫指标

王雪婷,王 燕,袁 凯

(烟台大学数学与信息科学学院,山东 烟台 264005)

1 引言与预备知识

假定G为连通图,顶点集为V(E)={v1,v2,…,vn},边集合为E(G)。一般来讲,图G中任意两个顶点之间的距离定义为连接它们的最短路径的长度。1993年,KLEIN和RANDIC基于电网络理论提出了新的距离函数[1]:图中任意两个顶点vi和vj之间的电阻距离定义为将G中每条边用单位电阻替代后得到的电网络中这两个节点之间的净有效电阻,记作ΩG(vi,vj)。新定义的电阻距离是电路图上的距离函数,相较于图中的最短路径,电阻距离更适合描述分子中的流体或波状通信,同时也被广泛应用于物理、化学等学科领域。

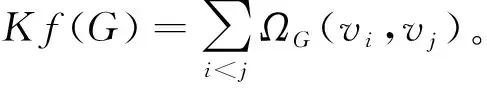
近些年来,图的基尔霍夫指标的计算得到了极大的发展。一些特殊图,如圈、完全图、连通图、循环图、凯莱图等的基尔霍夫指标已经有明确的计算公式[4-9]。 KLEIN等学者计算了一些在图上做一元或者二元运算所得到的图,如三角化、三角剖分、合成图[10-13]等的基尔霍夫指标,且所得的基尔霍夫指标是由原图的一些参数来表示,在一定程度上大大简化了这些图的基尔霍夫指标的计算过程。

对于连通图G,S(G)是将G中的每条边用P2(长度为2的路)代替。更进一步,在S(G)中,对原图G中的每个顶点添加两个悬挂点,并使这两个悬挂点相邻,所得到的新图记作RS(G)，见图1。

2010年,CHEN[14]得到了连通图S(G)中顶点对之间的电阻距离。 本文将在此基础上给出计算RS(G)的基尔霍夫指标的显性公式。

图1 图G与其所对应的RS(G)

2 RS(G)的电阻距离与基尔霍夫指标

本节将计算RS(G)的电阻距离、基尔霍夫指标、度乘以及度和基尔霍夫指标。 为了方便区分,分为两大部分进行计算。首先介绍计算中用到的已知结果。Ω、ΩS和ΩR分别表示G、S(G)和RS(G)中的电阻距离。

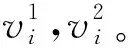
引理1 设vk是连通图G的一个割点,若顶点vi和vj属于G-vk的不同连通分支,则有ΩG(vi,vj)=ΩG(vi,vk)+ΩG(vk,vj)。

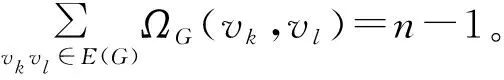
引理3[14]设G为连通图,NS(vkl)表示顶点vkl∈V1在图S(G)中的邻点集合,则S(G)中任意两顶点间的电阻距离为:

1)若vi,vj∈V(G),则有ΩS(vi,vj)=2Ω(vi,vj)。

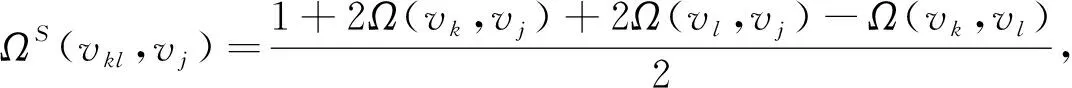
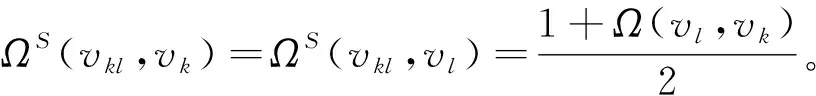
3)若vkl,vpq∈V1,NS(vkl)={vk,vl},NS(vpq)={vq,vp},则有

2.1 RS(G)的电阻距离与基尔霍夫指标

基于引理3,可以得到RS(G)中任意两个顶点之间的电阻距离,结果如下。

定理1G为连通图,则RS(G)中任意两个顶点间的电阻距离为:

1)若vi,vj∈V(G),则有

ΩR(vi,vj)=2Ω(vi,vj)。

(1)

2)若vkl∈V1,NS(vkl)={vk,vl},vj∈V(G),则有

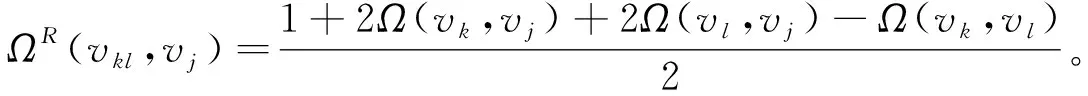
(2)

3)若vkl,vpq∈V1,NS(vkl)={vk,vl},NS(vpq)={vq,vp},则有

(3)

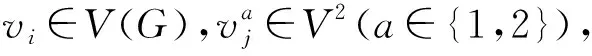
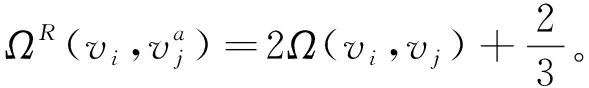
(4)

(5)

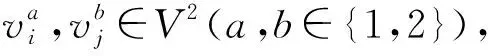
(6)

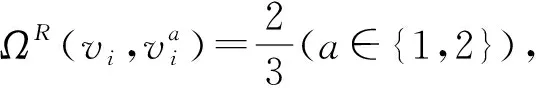
综上所述,定理1得证。

根据定理1和基尔霍夫指标的定义,可以计算得出RS(G)的基尔霍夫指标的显性公式。

定理2 假定G为具有n≥2个顶点、m条边的连通图,则

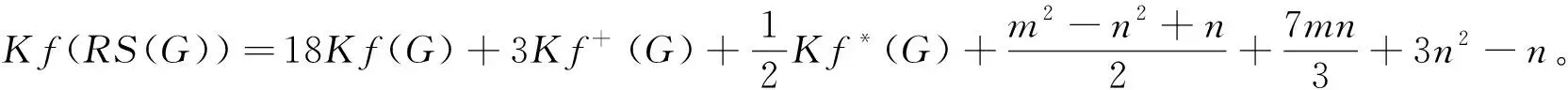
(7)

证明根据基尔霍夫指标的定义以及V(RS(G))=V(S(G))∪V2有

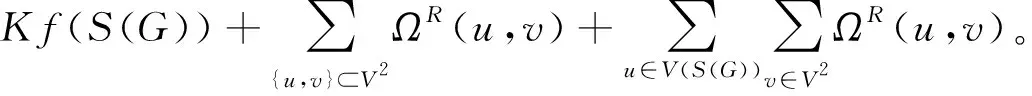
(8)

根据文献[11]的已知结果有

(9)

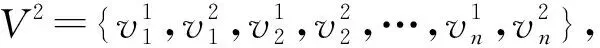
故有

(10)

因为V(S(G))=V(G)∪V1, 所以对于等式(8)中的第三个求和可以分为两个部分来计算：

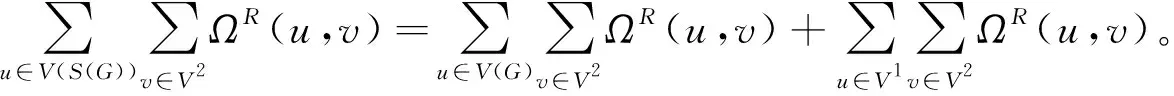
(11)

首先计算

(12)

其次

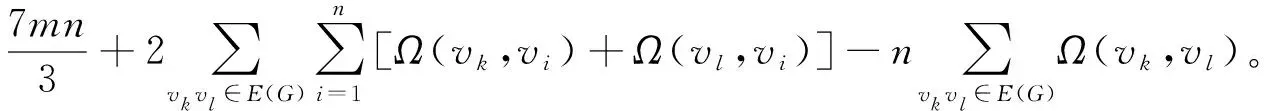
(13)

由引理2,

(14)

若令Ω(vi)表示G中所有顶点与vi之间的电阻距离之和,则等式(13)中第二部分求和公式可变形计算为

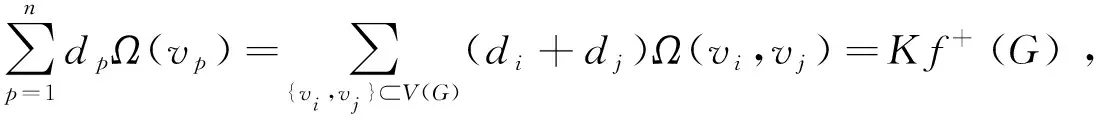
(15)

故将式(14)、(15)代入式(13),再将式(12)、(13)代回式(11),最后将式(9)、(10)、(11)代入式(8)得

2.2 RS(G)的度和基尔霍夫指标与度乘基尔霍夫指标

定理3 假定G为具有n≥2个顶点、m条边的连通图,则

Kf+(RS(G))=72Kf(G)+18Kf+(G)+4Kf*(G)+10n2+3m2+11mn+m-2n。

证明由度和基尔霍夫指标的定义以及V(RS(G))=V(S(G))∪V2有

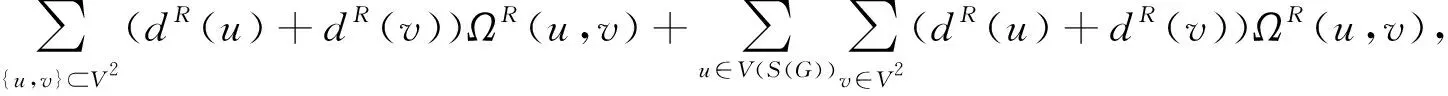
(16)

现将等式(16)的右边记为A1+A2+A3来进行运算。

首先计算A1,通过V(S(G))=V(G)∪V1可得

(17)

根据引理3,显然有

这片子是以卡扎菲为原型的，但有时候我觉得这同样也是以现在新一代小孩子为原型的嘛！观察一下周围的小孩子们，一个比一个大爷。孩子们最爱用的词就是“我”。“我”是他们的逻辑起点，也是终极目标。我的利益我的情绪至高无上。

(18)

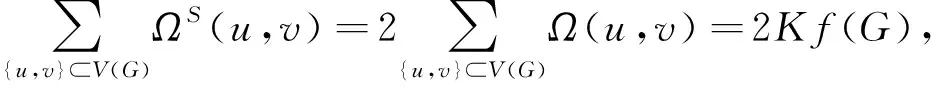
(19)

对于等式(17)右边的后面三部分,则可直接引用文献[10]、[11]的结果：

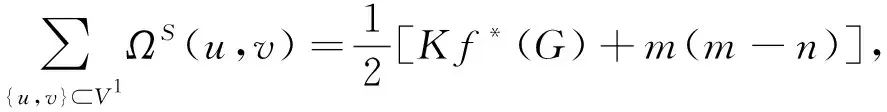
(20)

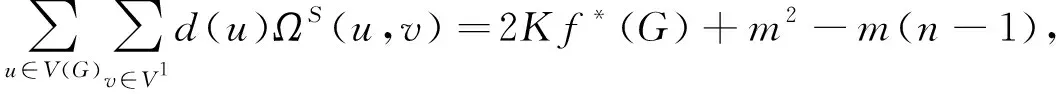
(21)

(22)

将等式(18)—(22)代入等式(17)中就可以得到

8Kf(G)+4Kf*(G)+6Kf+(G)+3m2-2n2-mn+m+2n。

(23)

其次计算A2,根据等式(10)显然

(24)

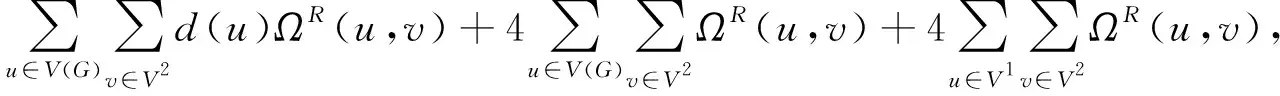
(25)

根据定理1,先计算等式(25)右边的第一部分

(26)

而式(25)右边的第二和第三部分已经由式(12)、(13)得出,故代入式(25)可得

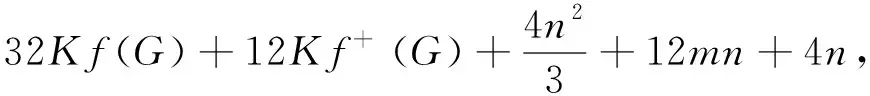
(27)

于是将式(23)、(24)和(27)代回式(16)就能得到

Kf+(RS(G))=8Kf(G)+4Kf*(G)+6Kf+(G)+3m2-2n2-mn+m+2n+

72Kf(G)+18Kf+(G)+4Kf*(G)+10n2+3m2+11mn+m-2n。

定理4 假定G为具有n≥2个顶点、m条边的连通图,则

证明由度乘基尔霍夫指标的定义以及V(RS(G))=V(S(G))∪V2有

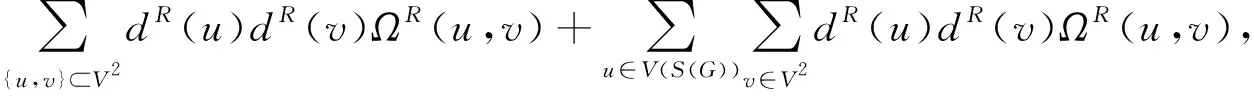
(28)

将等式(28)的右边三部分记为B1+B2+B3。

根据V(S(G))=V(G)∪V1先求B1：

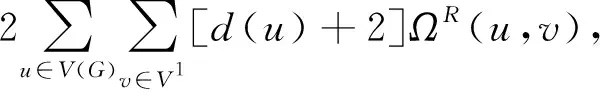
(29)

其中

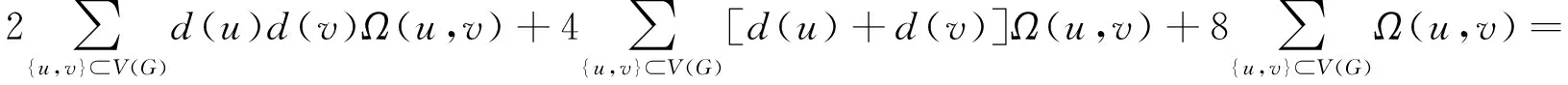
2Kf*(G)+4Kf+(G)+8Kf(G)，

(30)

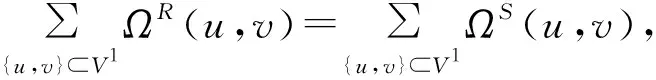
下面对等式(29)中的第三部分求和,根据等式(21)、(22)有

2Kf*(G)+2Kf+(G)+m2-n2+m+n。

(31)

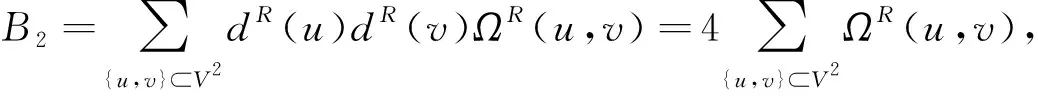
最后求等式(28)右边的B3:

在定理2和定理3的证明过程中,B3化简结果中的三部分已经求得结果,分别见等式(26)、(12)、(13)。

最后将求得的B1、B2、B3的结果代入等式(28)即可得到定理4:

Kf*(RS(G))=2Kf*(G)+4Kf+(G)+8Kf(G)+2[Kf*(G)+m(m-n)]+